Could you memorize a 60-by-60 multiplication table?  It has 1830 distinct numbers to memorize.

The answer today is an emphatic “No”!  Remember how long it took you to memorize the 12-by-12 table when you were a school child!

But 4000 years ago, the ancient Babylonians were doing it just fine—or at least “half” fine.  This is how.

How to Tally

In the ancient land of Sumer, the centralization of the economy, and the need of the government to control it, made it necessary to keep records of who owned what and who gave what to whom.  Scribes recorded transactions initially as tally marks pressed into soft clay around 5000 years ago, but one can only put so many marks on a clay tablet before it is full. 

Therefore, two inventions were needed to save space and time.  The first invention was a symbol that could stand in for a collection of tally marks.  Given the ten fingers we have on our hands, it is no surprise that this aggregate symbol stood for 10 units—almost every culture has some aspect of a base-10 number system.  With just two symbols repeated, numbers into the tens are easily depicted, as in Fig. 1. 

But by 4000 years ago, tallies were ranging into the millions, and a more efficient numerical notation was needed.  Hence, the second invention.

Place-value notation—an idea more abstract than the first—was so abstract that other cultures who drew from Mesopotamian mathematics, such as the Greeks and Romans, failed to recognize its power and adopt it. 

Today, we are so accustomed to place-value notation that it is hard to recognize how ingenious it is—how orders of magnitude are so easily encompassed in a few groups of symbols that keep track of thousands or millions at the same time as single units.  Our own decimal place-value system is from Hindu-Arabic numerals, which seems natural enough to us, but the mathematics of Old Babylon from the time of Hammurabi (1792 – 1750 BCE) was sexagesimal, based on the number 60. 

Our symbol for one hundred (100) using sexagesimal would be a pair of numbers (1,40) meaning 1×60+4×10. 

Our symbol for 119 would be (1, 59) meaning 1×60 + 5×10 + 9. 

Very large numbers are easily expressed.  Our symbol for 13,179,661 (using eight symbols) would be expressed in the sexagesimal system using only 5 symbols as (1, 1, 1, 1, 1) for 1×60⁴ + 1×60³ + 1×60² + 1×60 + 1. 

There has been much speculation on why a base 60 numeral system makes any sense.  The number does stand out because it has the largest number of divisors (1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30) of any smaller integer, and three of the divisors (2, 3, 5) are prime.  Babylonian mathematical manipulation relied heavily on fractions, and the availability of so many divisors may have been the chief advantage of the system.  The number the Babylonians used for the square root of 2 was (1; 24, 51, 10) = 1 + 24/60 + 51/60² + 10/60³ = 1.41421296 which is accurate to almost seven decimal places.  It has been pointed out [1] that this sexagesimal approximation for root-2 is what would be obtained if the Newton-Raphson method were used to find the root of the equation x²-2=0 starting from an initial guess of 3/2 = 1.5. 

Squares, Products and Differences

One of the most important quantities in any civilization is the measurement of land areas.  Land ownership is a measure of wealth and power and until recent times it was a requirement for authority or even citizenship.  This remains true today when land possession and ownership are one the bricks in the foundation of social stability and status.  The size of a McMansion is a status symbol, and the number of acres is a statement of wealth and power.  Even renters are acutely aware of how many square feet they have in their apartment or house. 

In ancient Sumer and Babylon, the possession of land was critically important, and it was necessary to measure land areas to track the accumulation or loss of ownership.  Because the measurement of area requires the multiplication of numbers, it is no surprise that multiplication was one of the first mathematical developments.

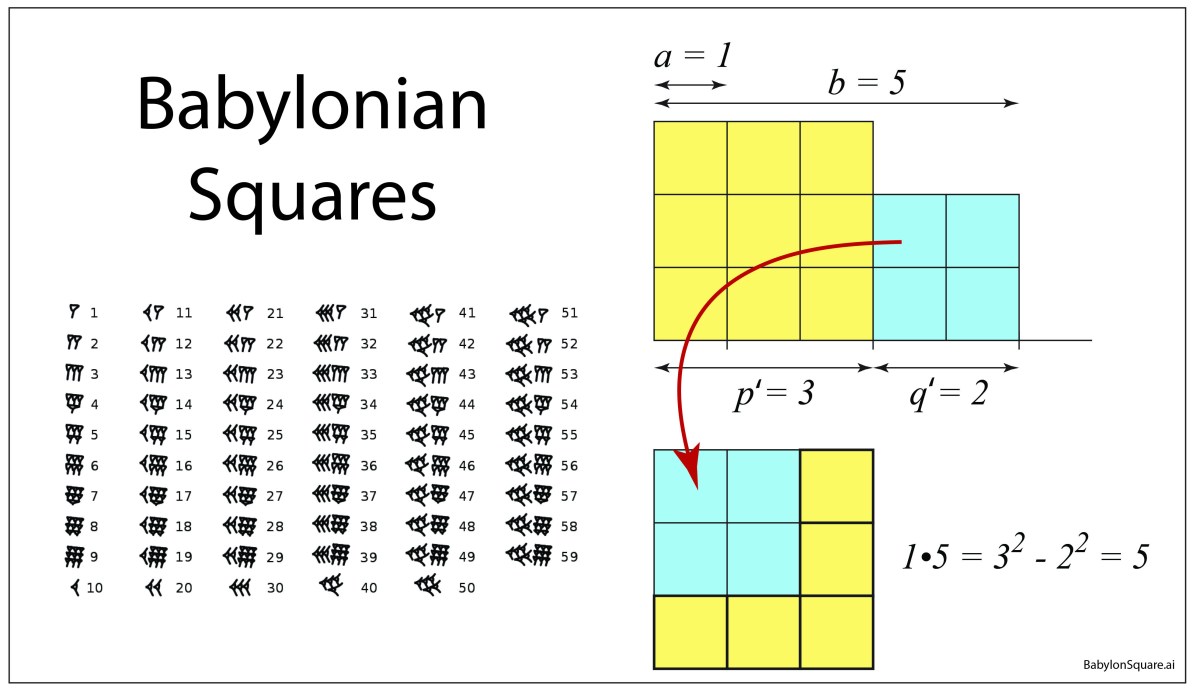
Babylonian mathematics depended heavily on squares—literally square geometric figures—and the manipulation of squares formed their central algorithm for multiplication.

The algorithm begins by associating to any pair of number (a, b) a unique second pair (p’, q’) where p’ = (a+b)/2 is the semi-sum (known as the average), and q’ = (b-a)/2 is the semi-difference.  The Babylonian mathematicians discovered that the product of the first pair is given by the difference in the squares of the second pair

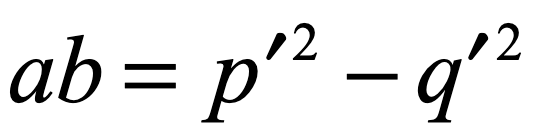
as depicted in Fig. 2. 

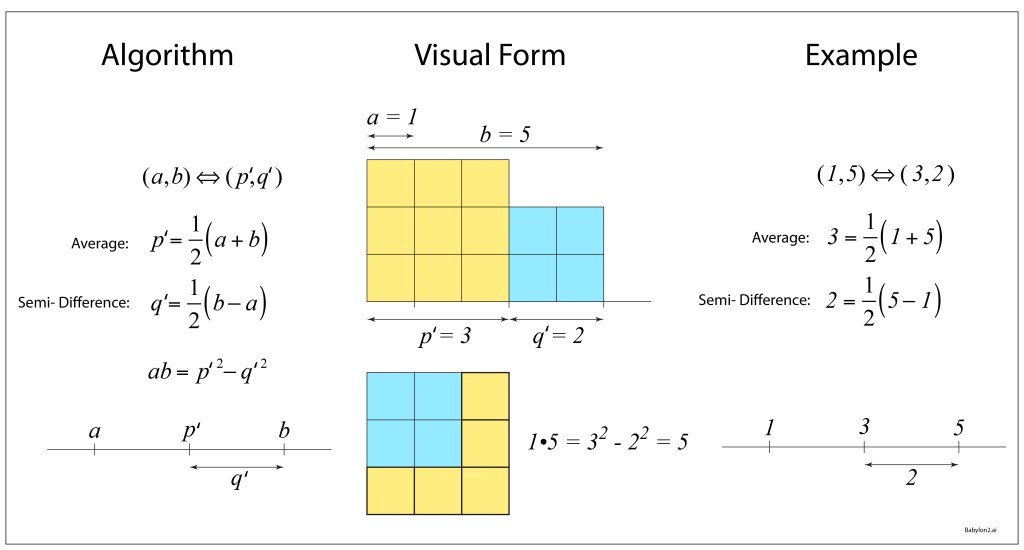
This simple relation between products, and the differences of squares, provides a significant savings in time and effort when constructing products of two large numbers—as long as the two numbers have the same parity.  That is the caveat!  The semi-sum and semi-difference each must be an integer, which only happens when the two numbers share the same parity (evenness or oddness).

Therefore, while a multiplication table up to 60 by 60 would have 60•61/4 = 915 distinct numbers to memorize, which could not be memorized easily, all squares up to 60² gives just 60 numbers to memorize, which is fewer than our children need to learn today. 

Therefore, with just 60 numbers, one could construct all 915 same-parity products of the 60 by 60 table using only sums and differences. 

Try it yourself.

---

[1] pg. 60, R. L. Cooke, The History of Mathematics: A Brief Course. (New York, John Wiley & Sons, 2012)