For a thirty-year old miller’s son with only one year of formal education, George Green had a strange hobby—he read papers in mathematics journals, mostly from France.  This was his escape from a dreary life running a flour mill on the outskirts of Nottingham, England, in 1823.  The tall wind mill owned by his father required 24-hour attention, with farmers depositing their grain at all hours and the mechanisms and sails needing constant upkeep.  During his one year in school when he was eight years old he had become fascinated by maths, and he nurtured this interest after leaving school one year later, stealing away to the top floor of the mill to pore over books he scavenged, devouring and exhausting all that English mathematics had to offer.  By the time he was thirty, his father’s business had become highly successful, providing George with enough wages to become a paying member of the private Nottingham Subscription Library with access to the Transactions of the Royal Society as well to foreign journals.  This simple event changed his life and changed the larger world of mathematics.

French Analysis in England

George Green was born in Nottinghamshire, England.  No record of his birth exists, but he was baptized in 1793, which may be assumed to be the year of his birth.  His father was a baker in Nottingham, but the food riots of 1800 forced him to move outside of the city to the town of Sneinton, where he bought a house and built an industrial-scale windmill to grind flour for his business.  He prospered enough to send his eight-year old son to Robert Goodacre’s Academy located on Upper Parliament Street in Nottingham.  Green was exceptionally bright, and after one year in school he had absorbed most of what the Academy could teach him, including a smattering of Latin and Greek as well as French along with what simple math that was offered.  Once he was nine, his schooling was over, and he took up the responsibility of helping his father run the mill, which he did faithfully, though unenthusiastically, for the next 20 years.  As the milling business expanded, his father hired a mill manager that took part of the burden off George.  The manager had a daughter Jane Smith, and in 1824 she had her first child with Green.  Six more children were born to the couple over the following fifteen years, though they never married.

Without adopting any microscopic picture of how electric or magnetic fields are produced or how they are transmitted through space, Green could still derive rigorous properties that are independent of any details of the microscopic model.

            During the 20 years after leaving Goodacre’s Academy, Green never gave up learning what he could, teaching himself to read French readily as well as mastering English mathematics.  The 1700’s and early 1800’s had been a relatively stagnant period for English mathematics.  After the priority dispute between Newton and Leibniz over the invention of the calculus, English mathematics had become isolated from continental advances.  This was part snobbery, but also part handicap as the English school struggled with Newton’s awkward fluxions while the continental mathematicians worked with Leibniz’ more fruitful differential notation.  One notable exception was Brook Taylor who developed the Taylor’s Series (and who grew up on the opposite end of the economic spectrum from Green, see my Blog on Taylor). However, the French mathematicians in the early 1800’s were especially productive, including such works as those by Lagrange, Laplace and Poisson.

            One block away from where Green lived stood the Free Grammar School overseen by headmaster John Topolis.  Topolis was a Cambridge graduate on a minor mission to update the teaching of mathematics in England, well aware that the advances on the continent were passing England by.  For instance, Topolis translated Laplace’s mathematically advanced Méchaniqe Celéste from French into English.  Topolis was also well aware of the work by the other French mathematicians and maintained an active scholarly output that eventually brought him back to Cambridge as Dean of Queen’s College in 1819 when Green was 26 years old.  There is no record whether Topolis and Green knew each other, but their close proximity and common interests point to a natural acquaintance.  One can speculate that Green may even have sought Topolis out, given his insatiable desire to learn more mathematics, and it is likely that Topolis would have introduced Green to the vibrant French school of mathematics.             

By the time Green joined the Nottingham Subscription Library, he must already have been well trained in basic mathematics, and membership in the library allowed him to request loans of foreign journals (sort of like Interlibrary Loan today).  With his library membership beginning in 1823, Green absorbed the latest advances in differential equations and must have begun forming a new viewpoint of the uses of mathematics in the physical sciences.  This was around the same time that he was beginning his family with Jane as well as continuing to run his fathers mill, so his mathematical hobby was relegated to the dark hours of the night.  Nonetheless, he made steady progress over the next five years as his ideas took rough shape and were refined until finally he took pen to paper, and this uneducated miller’s son began a masterpiece that would change the history of mathematics.

Essay on Mathematical Analysis of Electricity and Magnetism

By 1827 Green’s free-time hobby was about to bear fruit, and he took out a modest advertisement to announce its forthcoming publication.  Because he was an unknown, and unknown to any of the local academics (Topolis had already gone back to Cambridge), he chose vanity publishing and published out of pocket.   An Essay on the Application of Mathematical Analysis to the Theories of Electricity and Magnetism was printed in March of 1828, and there were 51 subscribers, mostly from among the members of the Nottingham Subscription Library who bought it at 7 shillings and 6 pence per copy, probably out of curiosity or sympathy rather than interest.  Few, if any, could have recognized that Green’s little essay contained several revolutionary elements.

            The topic of the essay was not remarkable, treating mathematical problems of electricity and magnetism, which was in vogue at that time.  As background, he had read works by Cavendish, Poisson, Arago, Laplace, Fourier, Cauchy and Thomas Young (probably Young’s Course of Lectures on Natural Philosopy and the Mechanical Arts (1807)).  He paid close attention to Laplace’s treatment of celestial mechanics and gravitation which had obvious strong analogs to electrostatics and the Coulomb force because of the common inverse square dependence. 

            One radical contribution in Green’s essay was his introduction of the potential function—one of the first uses of the concept of a potential function in mathematical physics—and he gave it its modern name.  Others had used similar constructions, such as Euler [1], D’Alembert [2], Laplace[3] and Poisson [4], but the use had been implicit rather than explicit.  Green shifted the potential function to the forefront, as a central concept from which one could derive other phenomena.  Another radical contribution from Green was his use of the divergence theorem.  This has tremendous utility, because it relates a volume integral to a surface integral.  It was one of the first examples of how measuring something over a closed surface could determine a property contained within the enclosed volume.  Gauss’ law is the most common example of this, where measuring the electric flux through a closed surface determines the amount of enclosed charge.  Lagrange in 1762 [5] and Gauss in 1813 [6] had used forms of the divergence theorem in the context of gravitation, but Green applied it to electrostatics where it has become known as Gauss’ law and is one of the four Maxwell equations.  Yet another contribution was Green’s use of linear superposition to determine the potential of a continuous charge distribution, integrating the potential of a point charge over a continuous charge distribution.  This was equivalent to defining what is today called a Green’s function, which is a common method to solve partial differential equations.

            A subtle contribution of Green’s Essay, but no less influential, was his adoption of a mathematical approach to a physics problem based on the fundamental properties of the mathematical structure rather than on any underlying physical model.  Without adopting any microscopic picture of how electric or magnetic fields are produced or how they are transmitted through space, he could still derive rigorous properties that are independent of any details of the microscopic model.  For instance, the inverse square law of both electrostatics and gravitation is a fundamental property of the divergence theorem (a mathematical theorem) in three-dimensional space.  There is no need to consider what space is composed of, such as the many differing models of the ether that were being proposed around that time.  He would apply this same fundamental mathematical approach in his later career as a Cambridge mathematician to explain the laws of reflection and refraction of light.

George Green: Cambridge Mathematician

A year after the publication of the Essay, Green’s father died a wealthy man, his milling business having become very successful.  Green inherited the family fortune, and he was finally able to leave the mill and begin devoting his energy to mathematics.  Around the same time he began working on mathematical problems with the support of Sir Edward Bromhead.  Bromhead was a Nottingham peer who had been one of the 51 subscribers to Green’s published Essay.  As a graduate of Cambridge he was friends with Herschel, Babbage and Peacock, and he recognized the mathematical genius in this self-educated miller’s son.  The two men spent two years working together on a pair of publications, after which Bromhead used his influence to open doors at Cambridge.

            In 1832, at the age of 40, George Green enrolled as an undergraduate student in Gonville and Caius College at Cambridge.  Despite his concerns over his lack of preparation, he won the first-year mathematics prize.  In 1838 he graduated as fourth wrangler only two positions behind the future famous mathematician James Joseph Sylvester (1814 – 1897).  Based on his work he was elected as a fellow of the Cambridge Philosophical Society in 1840.  Green had finally become what he had dreamed of being for his entire life—a professional mathematician.

            Green’s later papers continued the analytical dynamics trend he had established in his Essay by applying mathematical principles to the reflection and refraction of light. Cauchy had built microscopic models of the vibrating ether to explain and derive the Fresnel reflection and transmission coefficients, attempting to understand the structure of ether.  But Green developed a mathematical theory that was independent of microscopic models of the ether.  He believed that microscopic models could shift and change as newer models refined the details of older ones.  If a theory depended on the microscopic interactions among the model constituents, then it too would need to change with the times.  By developing a theory based on analytical dynamics, founded on fundamental principles such as minimization principles and geometry, then one could construct a theory that could stand the test of time, even as the microscopic understanding changed.  This approach to mathematical physics was prescient, foreshadowing the geometrization of physics in the late 1800’s that would lead ultimately to Einsteins theory of General Relativity.

Green’s Theorem and Greens Function

Green died in 1841 at the age of 49, and his Essay was mostly forgotten.  Ten years later a young William Thomson (later Lord Kelvin) was graduating from Cambridge and about to travel to Paris to meet with the leading mathematicians of the age.  As he was preparing for the trip, he stumbled across a mention of Green’s Essay but could find no copy in the Cambridge archives.  Fortunately, one of the professors had a copy that he lent Thomson.  When Thomson showed the work to Liouville and Sturm it caused a sensation, and Thomson later had the Essay republished in Crelle’s journal, finally bringing the work and Green’s name into the mainstream.

            In physics and mathematics it is common to name theorems or laws in honor of a leading figure, even if the they had little to do with the exact form of the theorem.  This sometimes has the effect of obscuring the historical origins of the theorem.  A classic example of this is the naming of Liouville’s theorem on the conservation of phase space volume after Liouville, who never knew of phase space, but who had published a small theorem in pure mathematics in 1838, unrelated to mechanics, that inspired Jacobi and later Boltzmann to derive the form of Liouville’s theorem that we use today.  The same is true of Green’s Theorem and Green’s Function.  The form of the theorem known as Green’s theorem was first presented by Cauchy [7] in 1846 and later proved by Riemann [8] in 1851.  The equation is named in honor of Green who was one of the early mathematicians to show how to relate an integral of a function over one manifold to an integral of the same function over a manifold whose dimension differed by one.  This property is a consequence of the Generalized Stokes Theorem (named after George Stokes), of which the Kelvin-Stokes Theorem, the Divergence Theorem and Green’s Theorem are special cases.

            Similarly, the use of Green’s function for the solution of partial differential equations was inspired by Green’s use of the superposition of point potentials integrated over a continuous charge distribution.  The Green’s function came into more general use in the late 1800’s and entered the mainstream of physics in the mid 1900’s [9].

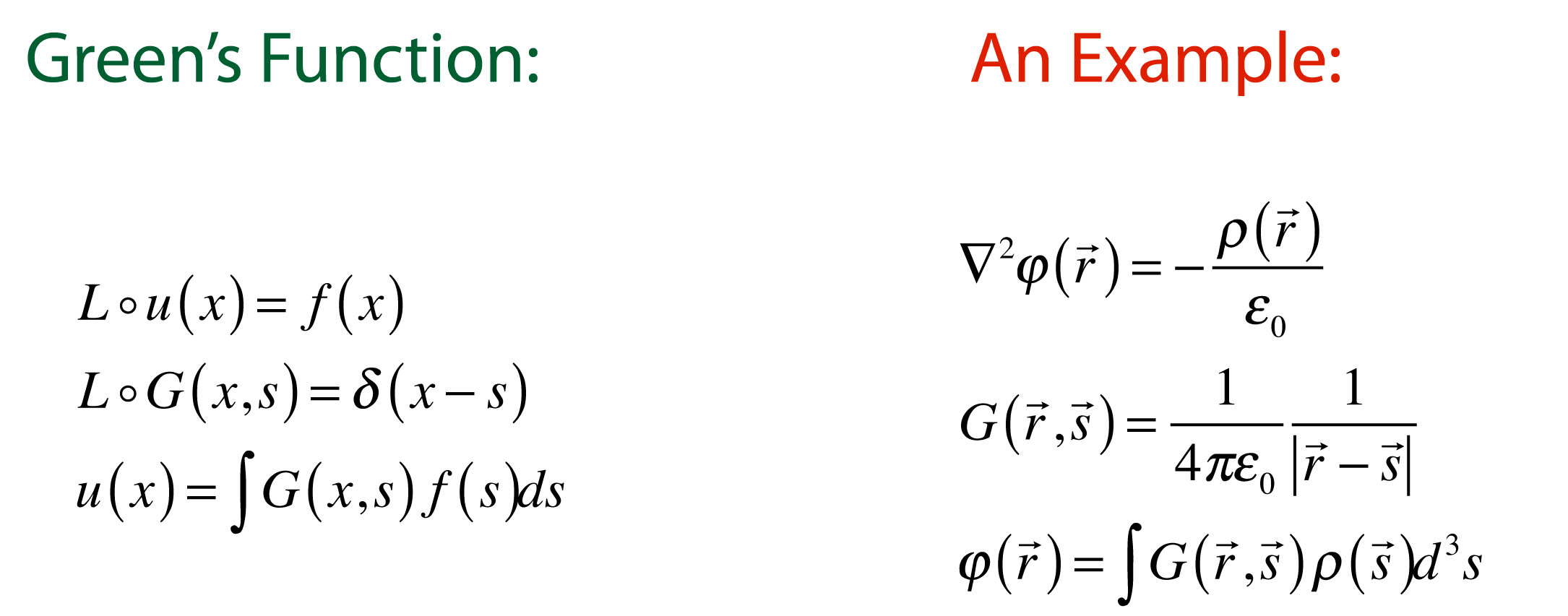
By David D. Nolte, Dec. 26, 2018

---

[1] L. Euler, Novi Commentarii Acad. Sci. Petropolitanae , 6 (1761)

[2] J. d’Alembert, “Opuscules mathématiques” , 1 , Paris (1761)

[3] P.S. Laplace, Hist. Acad. Sci. Paris (1782)

[4] S.D. Poisson, “Remarques sur une équation qui se présente dans la théorie des attractions des sphéroïdes” Nouveau Bull. Soc. Philomathique de Paris , 3 (1813) pp. 388–392

[5] Lagrange (1762) “Nouvelles recherches sur la nature et la propagation du son” (New researches on the nature and propagation of sound), Miscellanea Taurinensia (also known as: Mélanges de Turin ), 2: 11 – 172

[6] C. F. Gauss (1813) “Theoria attractionis corporum sphaeroidicorum ellipticorum homogeneorum methodo nova tractata,” Commentationes societatis regiae scientiarium Gottingensis recentiores, 2: 355–378

[7] Augustin Cauchy: A. Cauchy (1846) “Sur les intégrales qui s’étendent à tous les points d’une courbe fermée” (On integrals that extend over all of the points of a closed curve), Comptes rendus, 23: 251–255.

[8] Bernhard Riemann (1851) Grundlagen für eine allgemeine Theorie der Functionen einer veränderlichen complexen Grösse (Basis for a general theory of functions of a variable complex quantity), (Göttingen, (Germany): Adalbert Rente, 1867

[9] Schwinger, Julian (1993). “The Greening of quantum Field Theory: George and I”: 10283. arXiv:hep-ph/9310283