Albert Einstein defies condensation—it is impossible to condense his approach, his insight, his motivation—into a single word like “genius”.  He was complex, multifaceted, contradictory, revolutionary as well as conservative.  Some of his work was so simple that it is hard to understand why no-one else did it first, even when they were right in the middle of it.  Lorentz and Poincaré spring to mind—they had been circling the ideas of spacetime for decades—but never stepped back to see what the simplest explanation could be.  Einstein did, and his special relativity was simple and beautiful, and the math is just high-school algebra.  On the other hand, parts of his work—like gravitation—are so embroiled in mathematics and the religion of general covariance that it remains opaque to physics neophytes 100 years later and is usually reserved for graduate study. 

Yet there is a third thread in Einstein’s work that relies on pure intuition—neither simple nor complicated—but almost impossible to grasp how he made his leap.  This was the case when he proposed the real existence of the photon—the quantum particle of light.  For ten years after this proposal, it was considered by almost everyone to be his greatest blunder. It even came up when Planck was nominating Einstein for membership in the German Academy of Science. Planck said

That he may sometimes have missed the target of his speculations, as for example, in his hypothesis of light quanta, cannot really be held against him.

In this single statement, we have the father of the quantum being criticized by the father of the quantum discontinuity.

Max Planck’s Discontinuity

In histories of the development of quantum theory, the German physicist Max Planck (1858—1947) is characterized as an unlikely revolutionary.  He was an establishment man, in the stolid German tradition, who was already embedded in his career, in his forties, holding a coveted faculty position at the University of Berlin.  In his research, he was responding to a theoretical challenge issued by Kirchhoff many years ago in 1860 to find the function of temperature and wavelength that described and explained the observed spectrum of radiating bodies.  Planck was not looking for a revolution.  In fact, he was looking for the opposite.  One of his motivations in studying the thermodynamics of electromagnetic radiation was to rebut the statistical theories of Boltzmann.  Planck had never been convinced by the atomistic and discrete approach Boltzmann had used to explain entropy and the second law of thermodynamics.  With the continuum of light radiation he thought he had the perfect system that would show how entropy behaved in a continuous manner, without the need for discrete quantities. 

Therefore, Planck’s original intentions were to use blackbody radiation to argue against Boltzmann—to set back the clock.  For this reason, not only was Planck an unlikely revolutionary, he was a counter-revolutionary.  But Planck was a revolutionary because that is what he did, whatever his original intentions were, and he accepted his role as a revolutionary when he had the courage to stand in front of his scientific peers and propose a quantum hypothesis that lay at the heart of physics.

            Blackbody radiation, at the end of the nineteenth century, was a topic of keen interest and had been measured with high precision.  This was in part because it was such a “clean” system, having fundamental thermodynamic properties independent of any of the material properties of the black body, unlike the so-called ideal gases, which always showed some dependence on the molecular properties of the gas. The high-precision measurements of blackbody radiation were made possible by new developments in spectrometers at the end of the century, as well as infrared detectors that allowed very precise and repeatable measurements to be made of the spectrum across broad ranges of wavelengths. 

In 1893 the German physicist Wilhelm Wien (1864—1928) had used adiabatic expansion arguments to derive what became known as Wien’s Displacement Law that showed a simple linear relationship between the temperature of the blackbody and the peak wavelength.  Later, in 1896, he showed that the high-frequency behavior could be described by an exponential function of temperature and wavelength that required no other properties of the blackbody.  This was approaching the solution of Kirchhoff’s challenge of 1860 seeking a universal function.  However, at lower frequencies Wien’s approximation failed to match the measured spectrum.  In mid-year 1900, Planck was able to define a single functional expression that described the experimentally observed spectrum.  Planck had succeeded in describing black-body radiation, but he had not satisfied Kirchhoff’s second condition—to explain it. 

            Therefore, to describe the blackbody spectrum, Planck modeled the emitting body as a set of ideal oscillators.  As an expert in the Second Law, Planck derived the functional form for the radiation spectrum, from which he found the entropy of the oscillators that produced the spectrum.  However, once he had the form for the entropy, he needed to explain why it took that specific form.  In this sense, he was working backwards from a known solution rather than forwards from first principles.  Planck was at an impasse.  He struggled but failed to find any continuum theory that could work. 

Then Planck turned to Boltzmann’s statistical theory of entropy, the same theory that he had previously avoided and had hoped to discredit.  He described this as “an act of despair … I was ready to sacrifice any of my previous convictions about physics.”  In Boltzmann’s expression for entropy, it was necessary to “count” possible configurations of states.  But counting can only be done if the states are discrete.  Therefore, he lumped the energies of the oscillators into discrete ranges, or bins, that he called “quanta”.  The size of the bins was proportional to the frequency of the oscillator, and the proportionality constant had the units of Maupertuis’ quantity of action, so Planck called it the “quantum of action”. Finally, based on this quantum hypothesis, Planck derived the functional form of black-body radiation.

            Planck presented his findings at a meeting of the German Physical Society in Berlin on November 15, 1900, introducing the word quantum (plural quanta) into physics from the Latin word that means quantity [1].  It was a casual meeting, and while the attendees knew they were seeing an intriguing new physical theory, there was no sense of a revolution.  But Planck himself was aware that he had created something fundamentally new.  The radiation law of cavities depended on only two physical properties—the temperature and the wavelength—and on two constants—Boltzmann’s constant k_B and a new constant that later became known as Planck’s constant h = ΔE/f = 6.6×10^-34 J-sec.  By combining these two constants with other fundamental constants, such as the speed of light, Planck was able to establish accurate values for long-sought constants of nature, like Avogadro’s number and the charge of the electron.

            Although Planck’s quantum hypothesis in 1900 explained the blackbody radiation spectrum, his specific hypothesis was that it was the interaction of the atoms and the light field that was somehow quantized.  He certainly was not thinking in terms of individual quanta of the light field.

Einstein’s Quantum

When Einstein analyzed the properties of the blackbody radiation in 1905, using his deep insight into statistical mechanics, he was led to the inescapable conclusion that light itself must be quantized in amounts E = hf, where h is Planck’s constant and f is the frequency of the light field.  Although this equation is exactly the same as Planck’s from 1900, the meaning was completely different.  For Planck, this was the discreteness of the interaction of light with matter.  For Einstein, this was the quantum of light energy—whole and indivisible—just as if the light quantum were a particle with particle properties.  For this reason, we can answer the question posed in the title of this Blog—Einstein takes the honor of being the inventor of the quantum.

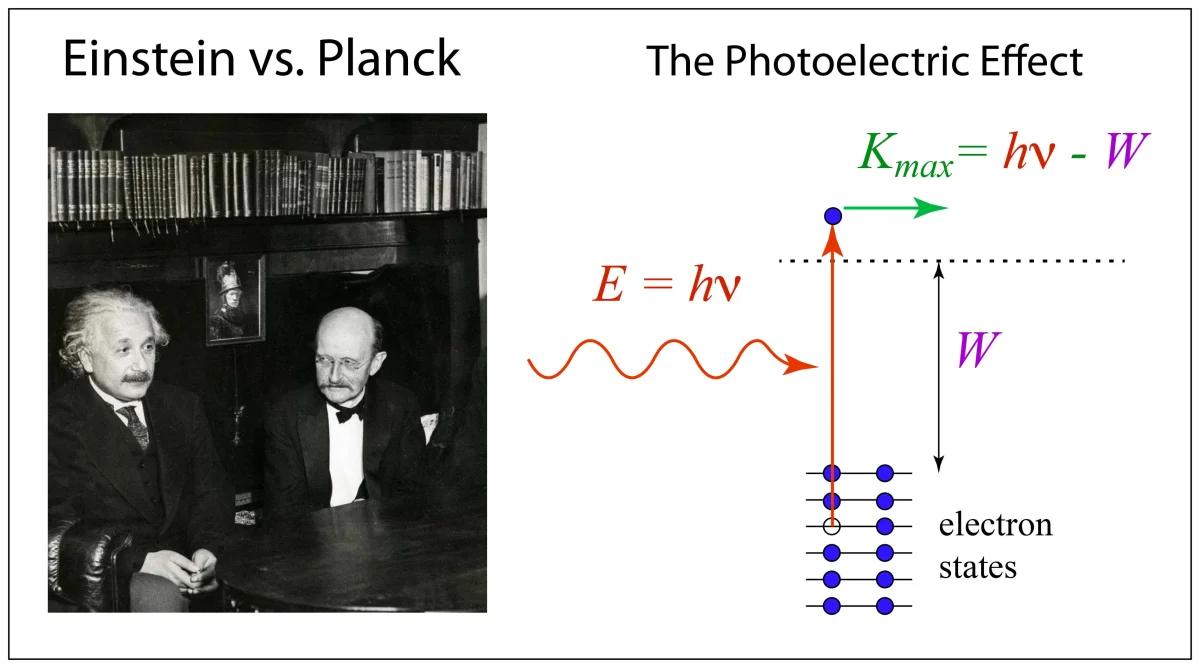
            Einstein’s clarity of vision is a marvel to behold even to this day.  His special talent was to take simple principles, ones that are almost trivial and beyond reproach, and to derive something profound.  In Special Relativity, he simply assumed the constancy of the speed of light and derived Lorentz’s transformations that had originally been based on obtuse electromagnetic arguments about the electron.  In General Relativity, he assumed that free fall represented an inertial frame, and he concluded that gravity must bend light.  In quantum theory, he assumed that the low-density limit of Planck’s theory had to be consistent with light in thermal equilibrium in thermal equilibrium with the black body container, and he concluded that light itself must be quantized into packets of indivisible energy quanta [2].  One immediate consequence of this conclusion was his simple explanation of the photoelectric effect for which the energy of an electron ejected from a metal by ultraviolet irradiation is a linear function of the frequency of the radiation.  Einstein published his theory of the quanta of light [3] as one of his four famous 1905 articles in Annalen der Physik in his Annus Mirabilis. 

            Einstein’s theory of light quanta was controversial and was slow to be accepted.  It is ironic that in 1914 when Einstein was being considered for a position at the University in Berlin, Planck himself, as he championed Einstein’s case to the faculty, implored his colleagues to accept Einstein despite his ill-conceived theory of light quanta [4].  This comment by Planck goes far to show how Planck, father of the quantum revolution, did not fully grasp, even by 1914, the fundamental nature and consequences of his original quantum hypothesis.  That same year, the American physicist Robert Millikan (1868—1953) performed a precise experimental measurement of the photoelectric effect, with the ostensible intention of proving Einstein wrong, but he accomplished just the opposite—providing clean experimental evidence confirming Einstein’s theory of the photoelectric effect. 

The Stimulated Emission of Light

About a year after Millikan proved that the quantum of energy associated with light absorption was absorbed as a whole quantum of energy that was not divisible, Einstein took a step further in his theory of the light quantum. In 1916 he published a paper in the proceedings of the German Physical Society that explored how light would be in a state of thermodynamic equilibrium when interacting with atoms that had discrete energy levels. Once again he used simple arguments, this time using the principle of detailed balance, to derive a new and unanticipated property of light—stimulated emission!

The stimulated emission of light occurs when an electron is in an excited state of a quantum system, like an atom, and an incident photon stimulates the emission of a second photon that has the same energy and phase as the first photon. If there are many atoms in the excited state, then this process leads to a chain reaction as 1 photon produces 2, and 2 produce 4, and 4 produce 8, etc. This exponential gain in photons with the same energy and phase is the origin of laser radiation. At the time that Einstein proposed this mechanism, lasers were half a century in the future, but he was led to this conclusion by extremely simple arguments about transition rates.

Detailed balance is a principle that states that in thermal equilibrium all fluxes are balanced. In the case of atoms with ground states and excited states, this principle requires that as many transitions occur from the ground state to the excited state as from the excited state to the ground state. The crucial new element that Einstein introduced was to distinguish spontaneous emission from stimulated emission. Just as the probability to absorb a photon must be proportional to the photon density, there must be an equivalent process that de-excites the atom that also must be proportional the photon density. In addition, an electron must be able to spontaneously emit a photon with a rate that is independent of photon density. This leads to distinct coefficients in the transition rate equations that are today called the “Einstein A and B coefficients”. The B coefficients relate to the photon density, while the A coefficient relates to spontaneous emission.

Using the principle of detailed balance together with his A and B coefficients as well as Boltzmann factors describing the number of excited states relative to ground state atoms in equilibrium at a given temperature, Einstein was able to derive an early form of what is today called the Bose-Einstein occupancy function for photons.

Derivation of the Einstein A and B Coefficients

Detailed balance requires the rate from m to n to be the same as the rate from n to m

where the first term is the spontaneous emission rate from the excited state m to the ground state n, the second term is the stimulated emission rate, and the third term (on the right) is the absorption rate from n to m. The numbers in each state are Nm and Nn, and the density of photons is ρ. The relative numbers in the excited state relative to the ground state is given by the Boltzmann factor

By assuming that the stimulated transition coefficient from n to m is the same as m to n, and inserting the Boltzmann factor yields

The Planck density of photons for ΔE = hf is

which yields the final relation between the spontaneous emission coefficient and the stimulated emission coefficient

The total emission rate is

where the p-bar is the average photon number in the cavity. One of the striking aspects of this derivation is that no assumptions are made about the physical mechanisms that determine the coefficient B. Only arguments of detailed balance are required to arrive at these results.

Einstein’s Quantum Legacy

Einstein was awarded the Nobel Prize in 1921 for the photoelectric effect, not for the photon nor for any of Einstein’s other theoretical accomplishments.  Even in 1921, the quantum nature of light remained controversial.  It was only in 1923, after the American physicist Arthur Compton (1892—1962) showed that energy and momentum were conserved in the scattering of photons from electrons, that the quantum nature of light began to be accepted.  The very next year, in 1924, the quantum of light was named the “photon” by the American American chemical physicist Gilbert Lewis (1875—1946). 

            A blog article like this, that attributes the invention of the quantum to Einstein rather than Planck, must say something about the irony of this attribution.  If Einstein is the father of the quantum, he ultimately was led to disinherit his own brain child.  His final and strongest argument against the quantum properties inherent in the Copenhagen Interpretation was his famous EPR paper which, against his expectations, launched the concept of entanglement that underlies the coming generation of quantum computers.

By David D. Nolte, Jan. 13, 2020

---

Read more about the History of Light and Optics in

“Interference” (Oxford University Press, 2023)

---

Einstein’s Quantum Timeline

1900 – Planck’s quantum discontinuity for the calculation of the entropy of blackbody radiation.

1905 – Einstein’s “Miracle Year”. Proposes the light quantum.

1911 – First Solvay Conference on the theory of radiation and quanta.

1913 – Bohr’s quantum theory of hydrogen.

1914 – Einstein becomes a member of the German Academy of Science.

1915 – Millikan measurement of the photoelectric effect.

1916 – Einstein proposes stimulated emission.

1921 – Einstein receives Nobel Prize for photoelectric effect and the light quantum. Third Solvay Conference on atoms and electrons.

1927 – Heisenberg’s uncertainty relation. Fifth Solvay International Conference on Electrons and Photons in Brussels. “First” Bohr-Einstein debate on indeterminancy in quantum theory.

1930 – Sixth Solvay Conference on magnetism. “Second” Bohr-Einstein debate.

1935 – Einstein-Podolsky-Rosen (EPR) paper on the completeness of quantum mechanics.

---

Selected Einstein Quantum Papers

Einstein, A. (1905). “Generation and conversion of light with regard to a heuristic point of view.” Annalen Der Physik 17(6): 132-148.

Einstein, A. (1907). “Die Plancksche Theorie der Strahlung und die Theorie der spezifischen W ̈arme.” Annalen der Physik 22: 180–190.

Einstein, A. (1909). “On the current state of radiation problems.” Physikalische Zeitschrift 10: 185-193.

Einstein, A. and O. Stern (1913). “An argument for the acceptance of molecular agitation at absolute zero.” Annalen Der Physik 40(3): 551-560.

Einstein, A. (1916). “Strahlungs-Emission un -Absorption nach der Quantentheorie.” Verh. Deutsch. Phys. Ges. 18: 318.

Einstein, A. (1917). “Quantum theory of radiation.” Physikalische Zeitschrift 18: 121-128.

Einstein, A., B. Podolsky and N. Rosen (1935). “Can quantum-mechanical description of physical reality be considered complete?” Physical Review 47(10): 0777-0780.

---

Notes

[1] M. Planck, “Elementary quanta of matter and electricity,” Annalen Der Physik, vol. 4, pp. 564-566, Mar 1901.

[2] Klein, M. J. (1964). Einstein’s First Paper on Quanta. The natural philosopher. D. A. Greenberg and D. E. Gershenson. New York, Blaidsdell. 3.

[3] A. Einstein, “Generation and conversion of light with regard to a heuristic point of view,” Annalen Der Physik, vol. 17, pp. 132-148, Jun 1905.

[4] Chap. 2 in “Mind at Light Speed“, by David Nolte (Free Press, 2001)

[5] Einstein, A. (1916). “Strahlungs-Emission un -Absorption nach der Quantentheorie.” Verh. Deutsch. Phys. Ges. 18: 318.

[6] Einstein, A. (1917). “Quantum theory of radiation.” Physikalische Zeitschrift 18: 121-128.

---