November 9, 2023November 30, 2023 by David D. Nolte

Timelines in the History of Light and Interference

At Light Speed
Adaptive Optics, Albert Michelson, Augustin Fresnel, Einstein, Francois Arago, Hanbury Brown Twiss, History of Optics, History of Physics, Holography, Interference, Interferometry, Quantum Optics, Thomas Young

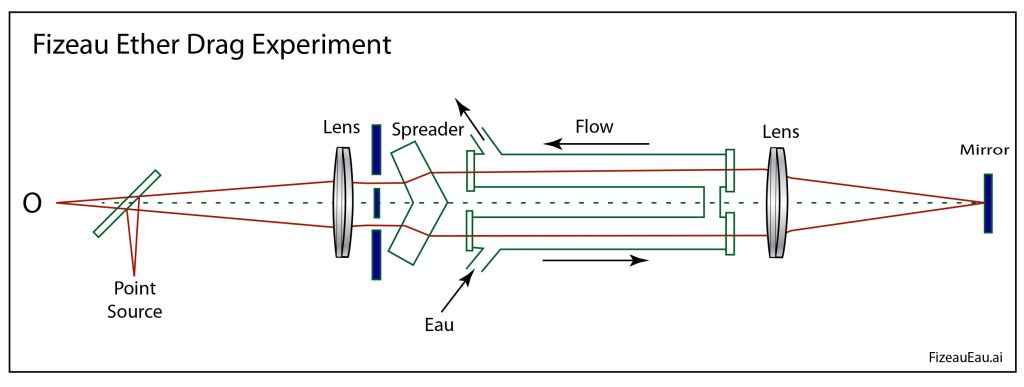
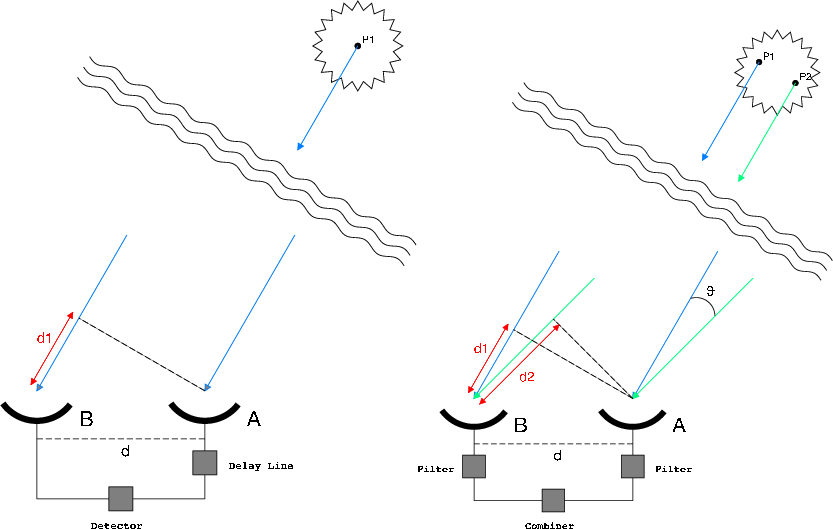
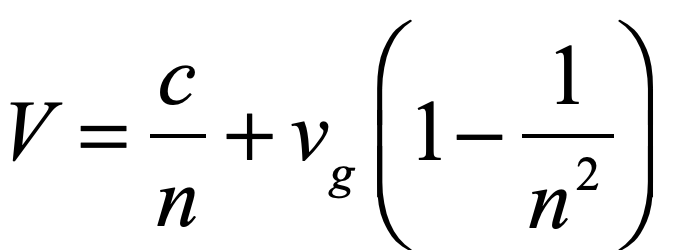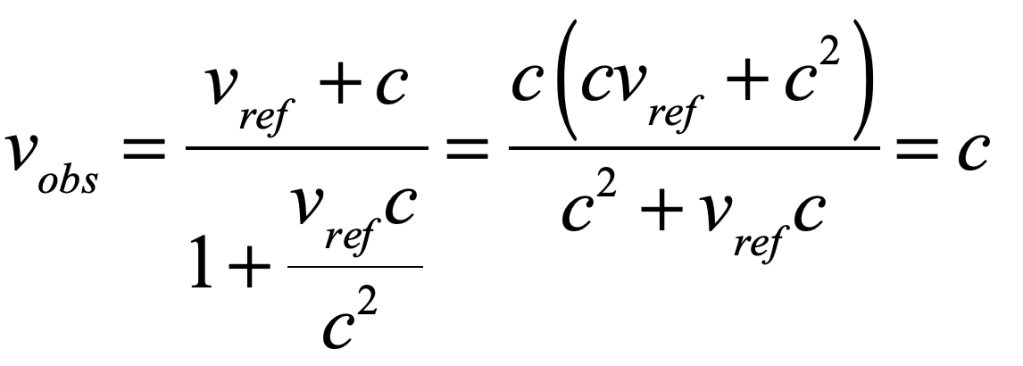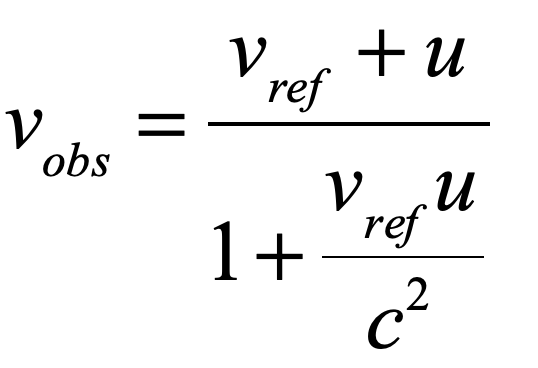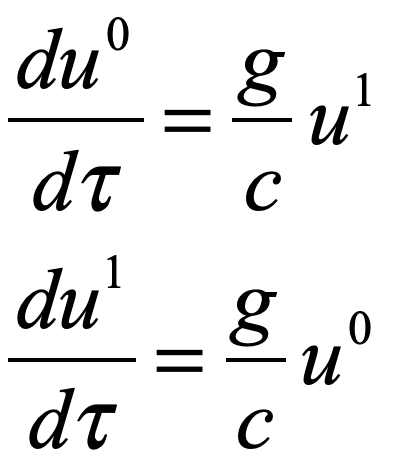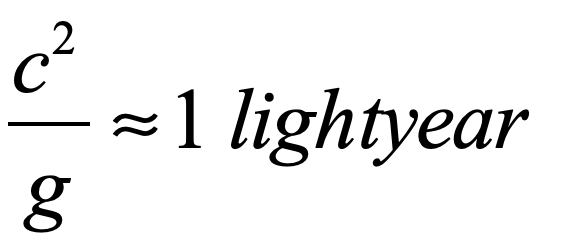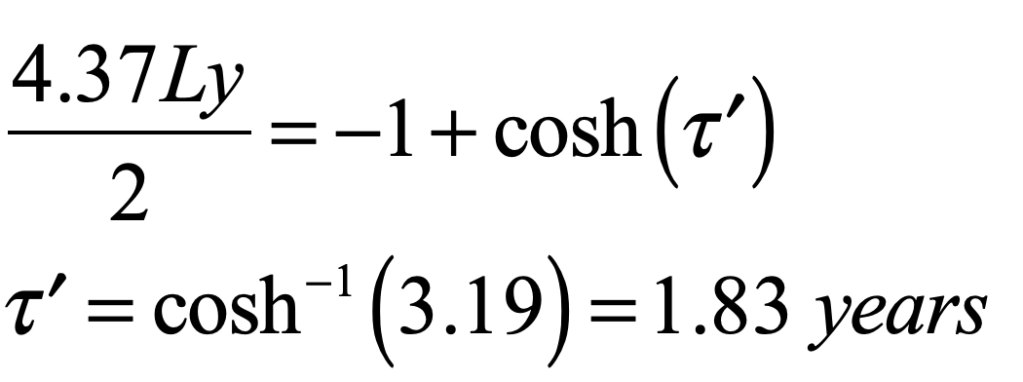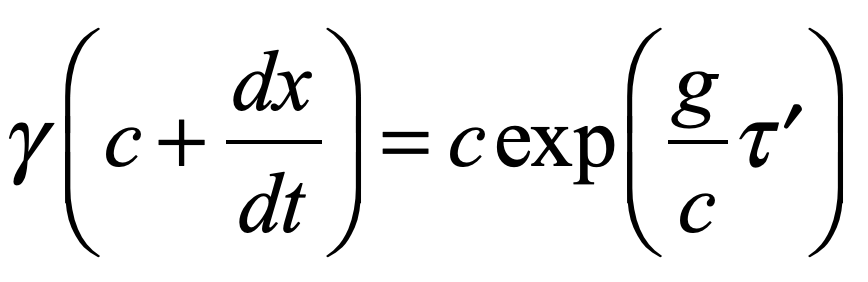Light is one of the most powerful manifestations of the forces of physics because it tells us about our reality. The interference of light, in particular, has led to the detection of exoplanets orbiting distant stars, discovery of the first gravitational waves, capture of images of black holes and much more. The stories behind the history of light and interference go to the heart of how scientists do what they do and what they often have to overcome to do it. These time-lines are organized along the chapter titles of the book Interference. They follow the path of theories of light from the first wave-particle debate, through the personal firestorms of Albert Michelson, to the discoveries of the present day in quantum information sciences.

Thomas Young Polymath: The Law of Interference
The Fresnel Connection: Particles versus Waves
At Light Speed: The Birth of Interferometry
After the Gold Rush: The Trials of Albert Michelson
Stellar Interference: Measuring the Stars
Across the Universe: Exoplanets, Black Holes and Gravitational Waves
Two Faces of Microscopy: Diffraction and Interference
Holographic Dreams of Princess Leia: Crossing Beams
Photon Interference: The Foundations of Quantum Communication
The Quantum Advantage: Interferometric Computing

1. Thomas Young Polymath: The Law of Interference

Thomas Young was the ultimate dabbler, his interests and explorations ranged far and wide, from ancient egyptology to naval engineering, from physiology of perception to the physics of sound and light. Yet unlike most dabblers who accomplish little, he made original and seminal contributions to all these fields. Some have called him the “Last Man Who Knew Everything“.

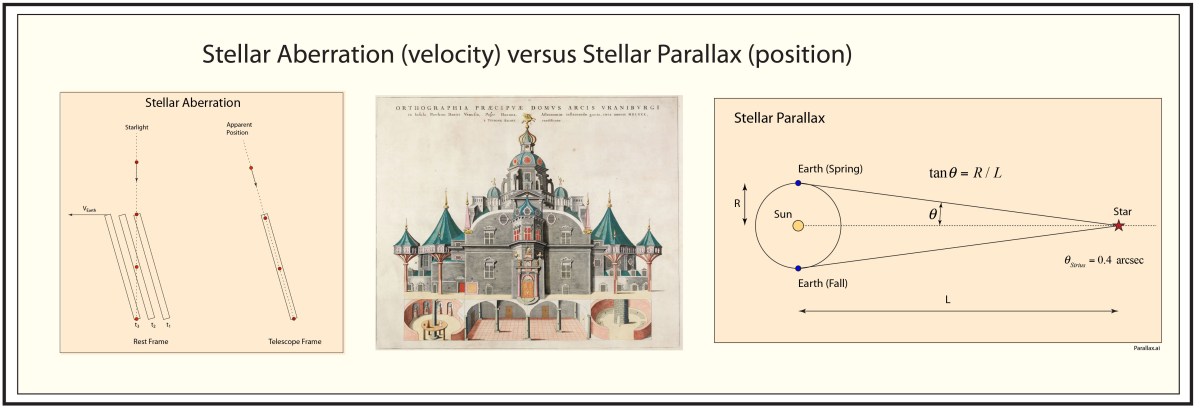
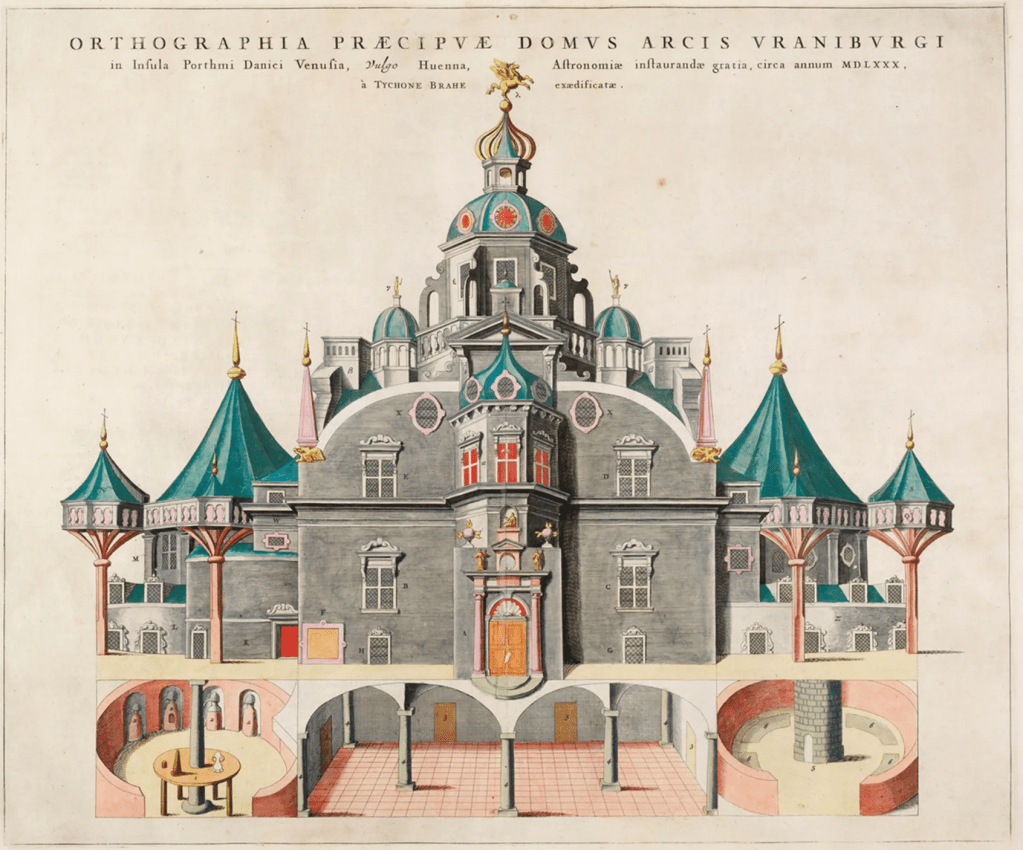
Topics: The Law of Interference. The Rosetta Stone. Benjamin Thompson, Count Rumford. Royal Society. Christiaan Huygens. Pendulum Clocks. Icelandic Spar. Huygens’ Principle. Stellar Aberration. Speed of Light. Double-slit Experiment.

1629 – Huygens born (1629 – 1695)

1642 – Galileo dies, Newton born (1642 – 1727)

1655 – Huygens ring of Saturn

1657 – Huygens patents the pendulum clock

1666 – Newton prismatic colors

1666 – Huygens moves to Paris

1669 – Bartholin double refraction in Icelandic spar

1670 – Bartholinus polarization of light by crystals

1671 – Expedition to Hven by Picard and Rømer

1673 – James Gregory bird-feather diffraction grating

1673 – Huygens publishes Horologium Oscillatorium

1675 – Rømer finite speed of light

1678 – Huygens and two crystals of Icelandic spar

1681 – Huygens returns to the Hague

1689 – Huyens meets Newton

1690 – Huygens Traite de la Lumiere

1695 – Huygens dies

1704 – Newton’s Opticks

1727 – Bradley abberation of starlight

1746 – Euler Nova theoria lucis et colorum

1773 – Thomas Young born

1786 – François Arago born (1786 – 1853)

1787 – Joseph Fraunhofer born (1787 – 1826)

1788 – Fresnel born in Broglie, Normandy (1788 – 1827)

1794 – École Polytechnique founded in Paris by Lazar Carnot and Gaspard Monge, Malus enters the Ecole

1794 – Young elected member of the Royal Society

1794 – Young enters Edinburg (cannot attend British schools because he was Quaker)

1795 – Young enters Göttingen

1796 – Young receives doctor of medicine, grand tour of Germany

1797 – Young returns to England, enters Emmanual College (converted to Church of England)

1798 – The Directory approves Napoleon’s Egyptian campaign, Battle of the Pyramids, Battle of the Nile

1799 – Young graduates from Cambridge

1799 – Royal Institution founded

1799 – Young Outlines

1800 – Young Sound and Light read to Royal Society,

1800 – Young Mechanisms of the Eye (Bakerian Lecture of the Royal Society)

1801 – Young Theory of Light and Colours, three color mechanism (Bakerian Lecture), Young considers interference to cause the colored films, first estimates of the wavelengths of different colors

1802 – Young begins series of lecturs at the Royal Institution (Jan. 1802 – July 1803)

1802 – Young names the principle (Law) of interference

1803 – Young’s 3^rd Bakerian Lecture, November. Experiments and Calculations Relative Physical to Optics, The Law of Interference

1807 – Young publishes A course of lectures on Natural Philosophy and the Mechanical Arts, based on Royal Institution lectures, two-slit experiment described

1808 – Malus polarization

1811 – Young appointed to St. Georges hospital

1813 – Young begins work on Rosetta stone

1814 – Young translates the demotic script on the stone

1816 – Arago visits Young

1818 – Young’s Encyclopedia article on Egypt

1822 – Champollion publishes translation of hieroglyphics

1827 – Young elected foreign member of the Institute of Paris

1829 – Young dies

2. The Fresnel Connection: Particles versus Waves

Augustin Fresnel was an intuitive genius whose talents were almost squandered on his job building roads and bridges in the backwaters of France until he was discovered and rescued by Francois Arago.

Topics: Particles versus Waves. Malus and Polarization. Agustin Fresnel. Francois Arago. Diffraction. Daniel Bernoulli. The Principle of Superposition. Joseph Fourier. Transverse Light Waves.

1665 – Grimaldi diffraction bands outside shadow

1673 – James Gregory bird-feather diffraction grating

1675 – Römer finite speed of light

1704 – Newton’s Optics

1727 – Bradley abberation of starlight

1774 – Jean-Baptiste Biot born

1786 – David Rittenhouse hairs-on-screws diffraction grating

1786 – François Arago born (1786 – 1853)

1787 – Fraunhofer born (1787 – 1826)

1788 – Fresnel born in Broglie, Normandy (1788 – 1827)

1790 – Fresnel moved to Cherbourg

1794 – École Polytechnique founded in Paris by Lazar Carnot and Gaspard Monge

1804 – Fresnel attends Ecole polytechnique in Paris at age 16

1806 – Fresnel graduated and attended the national school of bridges and highways

1808 – Malus polarization

1809 – Fresnel graduated from Les Ponts

1809 – Arago returns from captivity in Algiers

1811 – Arago publishes paper on particle theory of light

1811 – Arago optical ratotory activity (rotation)

1814 – Fraunhofer spectroscope (solar absorption lines)

1815 – Fresnel meets Arago in Paris on way home to Mathieu (for house arrest)

1815 – Fresnel first paper on wave properties of diffraction

1816 – Fresnel returns to Paris to demonstrate his experiments

1816 – Arago visits Young

1816 – Fresnel paper on interference as origin of diffraction

1817 – French Academy announces its annual prize competition: topic of diffraction

1817 – Fresnel invents and uses his “Fresnel Integrals”

1819 – Fresnel awarded French Academy prize for wave theory of diffraction

1819 – Arago and Fresnel transverse and circular (?) polarization

1821 – Fraunhofer diffraction grating

1821 – Fresnel light is ONLY transverse

1821 – Fresnel double refraction explanation

1823 – Fraunhofer 3200 lines per Paris inch

1826 – Publication of Fresnel’s award memoire

1827 – Death of Fresnel by tuberculosis

1840 – Ernst Abbe born (1840 – 1905)

1849 – Stokes distribution of secondary waves

1850 – Fizeau and Foucault speed of light experiments

3. At Light Speed

There is no question that Francois Arago was a swashbuckler. His life’s story reads like an adventure novel as he went from being marooned in hostile lands early in his career to becoming prime minister of France after the 1848 revolutions swept across Europe.

Topics: The Birth of Interferometry. Snell’s Law. Fresnel and Arago. The First Interferometer. Fizeau and Foucault. The Speed of Light. Ether Drag. Jamin Interferometer.

1671 – Expedition to Hven by Picard and Rømer

1704 – Newton’s Opticks

1729 – James Bradley observation of stellar aberration

1784 – John Michel dark stars

1804 – Young wave theory of light and ether

1808 – Malus discovery of polarization of reflected light

1810 – Arago search for ether drag

1813 – Fraunhofer dark lines in Sun spectrum

1819 – Fresnel’s double mirror

1820 – Oersted discovers electromagnetism

1821 – Faraday electromagnetic phenomena

1821 – Fresnel light purely transverse

1823 – Fresnel reflection and refraction based on boundary conditions of ether

1827 – Green mathematical analysis of electricity and magnetism

GreenEssayGoogle Download

1830 – Cauchy ether as elastic solid

1831 – Faraday electromagnetic induction

1831 – Cauchy ether drag

1831 – Maxwell born

1831 – Faraday electromagnetic induction

1834 – Lloyd’s mirror

1836 – Cauchy’s second theory of the ether

1838 – Green theory of the ether

1839 – Hamilton group velocity

1839 – MacCullagh properties of rotational ether

1839 – Cauchy ether with negative compressibility

1841 – Maxwell entered Edinburgh Academy (age 10) met P. G. Tait

1842 – Doppler effect

DopplerFarbigeLicht-3 Download

1845 – Faraday effect (magneto-optic rotation)

1846 – Haidinger fringes

1846 – Stokes’ viscoelastic theory of the ether

1847 – Maxwell entered Edinburgh University

1848 – Fizeau proposal of the Fizeau-Doppler effect

1849 – Fizeau speed of light

1850 – Maxwell at Cambridge, studied under Hopkins, also knew Stokes and Whewell

1852 – Michelson born Strelno, Prussia

1854 – Maxwell wins the Smith’s Prize (Stokes’ theorem was one of the problems)

1855 – Michelson’s immigrate to San Francisco through Panama Canal

1855 – Maxwell “On Faraday’s Line of Force”

1856 – Jamin interferometer

1856 – Thomson magneto-optics effects (of Faraday)

1857 – Clausius constructs kinetic theory, Mean molecular speeds

Clausius (1857)_Nature motion we call heat Download

1859 – Fizeau light in moving medium

1862 – Fizeau fringes

1865 – Maxwell “A Dynamical Theory of the Electromagnetic Field”

1867 – Thomson and Tait “Treatise on Natural Philosophy”

1867 – Thomson hydrodynamic vortex atom

1868 – Fizeau proposal for stellar interferometry

1870 – Maxwell introduced “curl”, “convergence” and “gradient”

1871 – Maxwell appointed to Cambridge

1873 – Maxwell “A Treatise on Electricity and Magnetism”

4. After the Gold Rush

No name is more closely connected to interferometry than that of Albert Michelson. He succeeded, sometimes at great personal cost, in launching interferometric metrology as one of the most important tools used by scientists today.

Albert A. Michelson, 1907 Nobel Prize. Image Credit.

Topics: The Trials of Albert Michelson. Hermann von Helmholtz. Michelson and Morley. Fabry and Perot.

1810 – Arago search for ether drag

1813 – Fraunhofer dark lines in Sun spectrum

1813 – Faraday begins at Royal Institution

1820 – Oersted discovers electromagnetism

1821 – Faraday electromagnetic phenomena

1827 – Green mathematical analysis of electricity and magnetism

1830 – Cauchy ether as elastic solid

1831 – Faraday electromagnetic induction

1831 – Cauchy ether drag

1831 – Maxwell born

1831 – Faraday electromagnetic induction

1836 – Cauchy’s second theory of the ether

1838 – Green theory of the ether

1839 – Hamilton group velocity

1839 – MacCullagh properties of rotational ether

1839 – Cauchy ether with negative compressibility

1841 – Maxwell entered Edinburgh Academy (age 10) met P. G. Tait

1842 – Doppler effect

1845 – Faraday effect (magneto-optic rotation)

1846 – Stokes’ viscoelastic theory of the ether

1847 – Maxwell entered Edinburgh University

1850 – Maxwell at Cambridge, studied under Hopkins, also knew Stokes and Whewell

1852 – Michelson born Strelno, Prussia

1854 – Maxwell wins the Smith’s Prize (Stokes’ theorem was one of the problems)

1855 – Michelson’s immigrate to San Francisco through Panama Canal

1855 – Maxwell “On Faraday’s Line of Force”

1856 – Jamin interferometer

1856 – Thomson magneto-optics effects (of Faraday)

1859 – Fizeau light in moving medium

1859 – Discovery of the Comstock Lode

1860 – Maxwell publishes first paper on kinetic theory.

1861 – Maxwell “On Physical Lines of Force” speed of EM waves and molecular vortices, molecular vortex model

1862 – Michelson at boarding school in SF

1865 – Maxwell “A Dynamical Theory of the Electromagnetic Field”

1867 – Thomson and Tait “Treatise on Natural Philosophy”

1867 – Thomson hydrodynamic vortex atom

1868 – Fizeau proposal for stellar interferometry

1869 – Michelson meets US Grant and obtained appointment to Annapolis

1870 – Maxwell introduced “curl”, “convergence” and “gradient”

1871 – Maxwell appointed to Cambridge

1873 – Big Bonanza at the Consolidated Virginia mine

1873 – Maxwell “A Treatise on Electricity and Magnetism”

1873 – Michelson graduates from Annapolis

1875 – Michelson instructor at Annapolis

1877 – Michelson married Margaret Hemingway

1878 – Michelson First measurement of the speed of light with funds from father in law

1879 – Michelson Begin collaborating with Newcomb

1879 – Maxwell proposes second-order effect for ether drift experiments

1879 – Maxwell dies

1880 – Michelson Idea for second-order measurement of relative motion against ether

1880 – Michelson studies in Europe with Helmholtz in Berlin

1881 – Michelson Measurement at Potsdam with funds from Alexander Graham Bell

1882 – Michelson in Paris, Cornu, Mascart and Lippman

1882 – Michelson Joined Case School of Applied Science

1884 – Poynting energy flux vector

1885 – Michelson Began collaboration with Edward Morley of Western Reserve

1885 – Lorentz points out inconsistency of Stokes’ ether model

1885 – Fitzgerald wheel and band model, vortex sponge

1886 – Michelson and Morley repeat the Fizeau moving water experiment

Michelson1886 Download

1887 – Michelson Five days in July experiment on motion relative to ether

1887 – Michelson-Morley experiment published

MichelsonMorley1887 Download

1887 – Voigt derivation of relativistic Doppler (with coordinate transformations)

Voigt1887 Download

1888 – Hertz generation and detection of radio waves

1889 – Michelson moved to Clark University at Worcester

1889 – Fitzgerald contraction

1889 – Lodge cogwheel model of electromagnetism

1890 – Michelson Proposed use of interferometry in astronomy

1890 – Thomson devises a mechanical model of MacCullagh’s rotational ether

1890 – Hertz Galileo relativity and ether drag

1891 – Mach-Zehnder

1891 – Michelson measures diameter of Jupiter’s moons with interferometry

1891 – Thomson vortex electromagnetism

1892 – 1893 Michelson measurement of the Paris meter

1893 – Sirks interferometer

1893 – Michelson moved to University of Chicago to head Physics Dept.

1893 – Lorentz contraction

1894 – Lodge primitive radio demonstration

1895 – Marconi radio

1896 – Rayleigh’s interferometer

1897 – Lodge no ether drag on laboratory scale

1898 – Pringsheim interferometer

1899 – Fabry-Perot interferometer

1899 – Michelson remarried

1901 – 1903 Michelson President of the APS

1905 – Poincaré names the Lorentz transformations

1905 – Einstein’s special theory of Relativity

1907 – Michelson Nobel Prize

1913 – Sagnac interferometer

1916 – Twyman-Green interferometer

1920 – Stellar interferometer on the Hooker 100-inch telescope (Betelgeuse)

1923 – 1927 Michelson presided over the National Academy of Sciences

1931 – Michelson dies

5. Stellar Interference

Learning from his attempts to measure the speed of light through the ether, Michelson realized that the partial coherence of light from astronomical sources could be used to measure their sizes. His first measurements using the Michelson Stellar Interferometer launched a major subfield of astronomy that is one of the most active today.

Topics: Measuring the Stars. Astrometry. Moons of Jupiter. Schwarzschild. Betelgeuse. Michelson Stellar Interferometer. Banbury Brown Twiss. Sirius. Adaptive Optics.

1838 – Bessel stellar parallax measurement with Fraunhofer telescope

1868 – Fizeau proposes stellar interferometry

1873 – Stephan implements Fizeau’s stellar interferometer on Sirius, sees fringes

1880 – Michelson Idea for second-order measurement of relative motion against ether

1880 – 1882 Michelson Studies in Europe (Helmholtz in Berlin, Quincke in Heidelberg, Cornu, Mascart and Lippman in Paris)

1881 – Michelson Measurement at Potsdam with funds from Alexander Graham Bell

1881 – Michelson Resigned from active duty in the Navy

1883 – Michelson Joined Case School of Applied Science

1889 – Michelson moved to Clark University at Worcester

1890 – Michelson develops mathematics of stellar interferometry

1891 – Michelson measures diameters of Jupiter’s moons

Michelson1891 Download

1893 – Michelson moves to University of Chicago to head Physics Dept.

1896 – Schwarzschild double star interferometry

1907 – Michelson Nobel Prize

1908 – Hale uses Zeeman effect to measure sunspot magnetism

1910 – Taylor single-photon double slit experiment

1915 – Proxima Centauri discovered by Robert Innes

1916 – Einstein predicts gravitational waves

1920 – Stellar interferometer on the Hooker 100-inch telescope (Betelgeuse)

Michelson1921 Download

1947 – McCready sea interferometer observes rising sun (first fringes in radio astronomy

1952 – Ryle radio astronomy long baseline

1954 – Hanbury-Brown and Twiss radio intensity interferometry

1956 – Hanbury-Brown and Twiss optical intensity correlation, Sirius (optical)

1958 – Jennison closure phase

1970 – Labeyrie speckle interferometry

1974 – Long-baseline radio interferometry in practice using closure phase

1974 – Johnson, Betz and Townes: IR long baseline

1975 – Labeyrie optical long-baseline

1982 – Fringe measurements at 2.2 microns Di Benedetto

1985 – Baldwin closure phase at optical wavelengths

1991 – Coude du Foresto single-mode fibers with separated telescopes

1993 – Nobel prize to Hulse and Taylor for binary pulsar

1995 – Baldwin optical synthesis imaging with separated telescopes

1991 – Mayor and Queloz Doppler pull of 51 Pegasi

1999 – Upsilon Andromedae multiple planets

2009 – Kepler space telescope launched

2014 – Kepler announces 715 planets

2015 – Kepler-452b Earthlike planet in habitable zone

2015 – First detection of gravitational waves

2016 – Proxima Centauri b exoplanet confirmed

2017 – Nobel prize for gravitational waves

2018 – TESS (Transiting Exoplanet Survey Satellite)

2019 – Mayor and Queloz win Nobel prize for first exoplanet

2019 – First direct observation of exoplanet using interferometry

2019 – First image of a black hole obtained by very-long-baseline interferometry

6. Across the Universe

Stellar interferometry is opening new vistas of astronomy, exploring the wildest occupants of our universe, from colliding black holes half-way across the universe (LIGO) to images of neighboring black holes (EHT) to exoplanets near Earth that may harbor life.

Image of the supermassive black hole in M87 from Event Horizon Telescope.

Topics: Gravitational Waves, Black Holes and the Search for Exoplanets. Nulling Interferometer. Event Horizon Telescope. M87 Black Hole. Long Baseline Interferometry. LIGO.

1947 – Virgo A radio source identified as M87

1953 – Horace W. Babcock proposes adaptive optics (AO)

Babcock1953 Download

1958 – Jennison closure phase

1967 – First very long baseline radio interferometers (from meters to hundreds of km to thousands of km within a single year)

1967 – Ranier Weiss begins first prototype gravitational wave interferometer

1967 – Virgo X-1 x-ray source (M87 galaxy)

1970 – Poul Anderson’s Tau Zero alludes to AO in science fiction novel

1973 – DARPA launches adaptive optics research with contract to Itek, Inc.

1974 – Wyant (Itek) white-light shearing interferometer

1974 – Long-baseline radio interferometry in practice using closure phase

1975 – Hardy (Itek) patent for adaptive optical system

1975 – Weiss funded by NSF to develop interferometer for GW detection

1977 – Demonstration of AO on Sirius (Bell Labs and Berkeley)

1980 – Very Large Array (VLA) 6 mm to 4 meter wavelengths

1981 – Feinleib proposes atmospheric laser backscatter

1982 – Will Happer at Princeton proposes sodium guide star

1982 – Fringe measurements at 2.2 microns (Di Benedetto)

1983 – Sandia Optical Range demonstrates artificial guide star (Rayleigh)

1983 – Strategic Defense Initiative (Star Wars)

1984 – Lincoln labs sodium guide star demo

1984 – ESO plans AO for Very Large Telescope (VLT)

1985 – Laser guide star (Labeyrie)

1985 – Closure phase at optical wavelengths (Baldwin)

1988 – AFWL names Starfire Optical Range, Kirtland AFB outside Albuquerque

1988 – Air Force Maui Optical Site Schack-Hartmann and 241 actuators (Itek)

1988 – First funding for LIGO feasibility

1989 – 19-element-mirror Double star on 1.5m telescope in France

1989 – VLT approved for construction

1990 – Launch of the Hubble Space Telescope

1991 – Single-mode fibers with separated telescopes (Coude du Foresto)

1992 – ADONIS

1992 – NSF requests declassification of AO

1993 – VLBA (Very Long Baseline Array) 8,611 km baseline 3 mm to 90 cm

1994 – Declassification completed

1994 – Curvature sensor 3.6m Canada-France-Hawaii

1994 – LIGO funded by NSF, Barish becomes project director

1995 – Optical synthesis imaging with separated telescopes (Baldwin)

1995 – Doppler pull of 51 Pegasi (Mayor and Queloz)

1998 – ESO VLT first light

1998 – Keck installed with Schack-Hartmann

1999 – Upsilon Andromedae multiple planets

2000 – Hale 5m Palomar Schack-Hartmann

2001 – NAOS-VLT adaptive optics

2001 – VLTI first light (MIDI two units)

2002 – LIGO operation begins

2007 – VLT laser guide star

2007 – VLTI AMBER first scientific results (3 units)

2009 – Kepler space telescope launched

2009 – Event Horizon Telescope (EHT) project starts

2010 – Large Binocular Telescope (LBT) 672 actuators on secondary mirror

2010 – End of first LIGO run. No events detected. Begin Enhanced LIGO upgrade.

2011 – SPHERE-VLT 41×41 actuators (1681)

2012 – Extremely Large Telescope (ELT) approved for construction

2014 – Kepler announces 715 planets

2015 – Kepler-452b Earthlike planet in habitable zone

2015 – First detection of gravitational waves (LIGO)

2015 – LISA Pathfinder launched

2016 – Second detection at LIGO

2016 – Proxima Centauri b exoplanet confirmed

2016 – GRAVITY VLTI (4 units)

2017 – Nobel prize for gravitational waves

2018 – TESS (Transiting Exoplanet Survey Satellite) launched

2018 – MATTISE VLTI first light (combining all units)

2019 – Mayor and Queloz win Nobel prize

2019 – First direct observation of exoplanet using interferometry at LVTI

2019 – First image of a black hole obtained by very-long-baseline interferometry (EHT)

2020 – First neutron-star black-hole merger detected

2020 – KAGRA (Japan) online

2024 – LIGO India to go online

2025 – First light for ELT

2034 – Launch date for LISA

7. Two Faces of Microscopy

From the astronomically large dimensions of outer space to the microscopically small dimensions of inner space, optical interference pushes the resolution limits of imaging.

Topics: Diffraction and Interference. Joseph Fraunhofer. Diffraction Gratings. Henry Rowland. Carl Zeiss. Ernst Abbe. Phase-contrast Microscopy. Super-resolution Micrscopes. Structured Illumination.

1021 – Al Hazeni manuscript on Optics

1284 – First eye glasses by Salvino D’Armate

1590 – Janssen first microscope

1609 – Galileo first compound microscope

1625 – Giovanni Faber coins phrase “microscope”

1665 – Hook’s Micrographia

1676 – Antonie van Leeuwenhoek microscope

1787 – Fraunhofer born

1811 – Fraunhofer enters business partnership with Utzschneider

1816 – Carl Zeiss born

1821 – Fraunhofer first diffraction publication

1823 – Fraunhofer second diffraction publication 3200 lines per Paris inch

1830 – Spherical aberration compensated by Joseph Jackson Lister

1840 – Ernst Abbe born

1846 – Zeiss workshop in Jena, Germany

1850 – Fizeau and Foucault speed of light

1851 – Otto Schott born

1859 – Kirchhoff and Bunsen theory of emission and absorption spectra

1866 – Abbe becomes research director at Zeiss

1874 – Ernst Abbe equation on microscope resolution

1874 – Helmholtz image resolution equation

1880 – Rayleigh resolution

1888 – Hertz waves

1888 – Frits Zernike born

1925 – Zsigmondy Nobel Prize for light-sheet microscopy

1931 – Transmission electron microscope by Ruske and Knoll

1932 – Phase contrast microscope by Zernicke

1942 – Scanning electron microscope by Ruska

1949 – Mirau interferometric objective

1952 – Nomarski differential phase contrast microscope

1953 – Zernicke Nobel prize

1955 – First discussion of superresolution by Toraldo di Francia

1957 – Marvin Minsky patents confocal principle

1962 – Green flurescence protein (GFP) Shimomura, Johnson and Saiga

1966 – Structured illumination microscopy by Lukosz

1972 – CAT scan

1978 – Cremer confocal laser scanning microscope

1978 – Lohman interference microscopy

1981 – Binnig and Rohrer scanning tunneling microscope (STM)

1986 – Microscopy Nobel Prize: Ruska, Binnig and Rohrer

1990 – 4PI microscopy by Stefan Hell

1992 – GFP cloned

1993 – STED by Stefan Hell

1993 – Light sheet fluorescence microscopy by Spelman

1995 – Structured illumination microscopy by Guerra

1995 – Gustafsson image interference microscopy

1999 – Gustafsson I⁵M

2004 – Selective plane illumination microscopy (SPIM)

2006 – PALM and STORM (Betzig and Zhuang)

2014 – Nobel Prize (Hell, Betzig and Moerner)

8. Holographic Dreams of Princess Leia

The coherence of laser light is like a brilliant jewel that sparkles in the darkness, illuminating life, probing science and projecting holograms in virtual worlds.

Topics: Crossing Beams. Denis Gabor. Wavefront Reconstruction. Holography. Emmett Leith. Lasers. Ted Maiman. Charles Townes. Optical Maser. Dynamic Holography. Light-field Imaging.

1900 – Dennis Gabor born

1926 – Hans Busch magnetic electron lens

1927 – Gabor doctorate

1931 – Ruska and Knoll first two-stage electron microscope

1942 – Lawrence Bragg x-ray microscope

1948 – Gabor holography paper in Nature

1949 – Gabor moves to Imperial College

1950 – Lamb possibility of population inversion

1951 – Purcell and Pound demonstration of population inversion

1952 – Leith joins Willow Run Labs

1953 – Townes first MASER

1957 – SAR field trials

1957 – Gould coins LASER

1958 – Schawlow and Townes proposal for optical maser

1959 – Shawanga Lodge conference

1960 – Maiman first laser: pink ruby

1960 – Javan first gas laser: HeNe at 1.15 microns

1961 – Leith and Upatnieks wavefront reconstruction

1962 – HeNe laser in the visible at 632.8 nm

1962 – First laser holograms (Leith and Upatnieks)

1963 – van Heerden optical information storage

1963 – Leith and Upatnieks 3D holography

1966 – Ashkin optically-induced refractive index changes

1966 – Leith holographic information storage in 3D

1968 – Bell Labs holographic storage in Lithium Niobate and Tantalate

1969 – Kogelnik coupled wave theory for thick holograms

1969 – Electrical control of holograms in SBN

1970 – Optically induced refractive index changes in Barium Titanate

1971 – Amodei transport models of photorefractive effect

1971 – Gabor Nobel prize

1972 – Staebler multiple holograms

1974 – Glass and von der Linde photovoltaic and photorefractive effects, UV erase

1977 – Star Wars movie

1981 – Huignard two-wave mixing energy transfer

2012 – Coachella Music Festival

9. Photon Interference

What is the image of one photon interfering? Better yet, what is the image of two photons interfering? The answer to this crucial question laid the foundation for quantum communication.

Topics: The Beginnings of Quantum Communication. EPR paradox. Entanglement. David Bohm. John Bell. The Bell Inequalities. Leonard Mandel. Single-photon Interferometry. HOM Interferometer. Two-photon Fringes. Quantum cryptography. Quantum Teleportation.

1900 – Planck (1901). “Law of energy distribution in normal spectra.” [1]

Planck-1901-Annalen_der_Physik Download

1905 – A. Einstein (1905). “Generation and conversion of light wrt a heuristic point of view.” [2]

1909 – A. Einstein (1909). “On the current state of radiation problems.” [3]

1909 – Single photon double-slit experiment, G.I. Taylor [4]

1915 – Milliken photoelectric effect

1916 – Einstein predicts stimulated emission

1923 –Compton, Arthur H. (May 1923). Quantum Theory of the Scattering of X-Rays.[5]

1926 – Gilbert Lewis names “photon”

1926 – Dirac: photons interfere only with themselves

1927 – D. Dirac, P. A. M. (1927). Emission and absorption of radiation [6]

1932 – von Neumann textbook on quantum physics

1932 – E. P. Wigner: Phys. Rev. 40, 749 (1932)

1935 – EPR paper, A. Einstein, B. Podolsky, N. Rosen: Phys. Rev. 47 , 777 (1935)

1935 – Reply to EPR, N. Bohr: Phys. Rev. 48 , 696 (1935)

1935 – Schrödinger (1935 and 1936) on entanglement (cat?) “Present situation in QM”

1948 – Gabor holography

1950 – Wu correlated spin generation from particle decay

1951 – Bohm alternative form of EPR gedankenexperiment (quantum textbook)

1952 – Bohm nonlocal hidden variable theory[7]

1953 – Schwinger: Coherent states

1956 – Photon bunching, R. Hanbury-Brown, R.W. Twiss: Nature 177 , 27 (1956)

1957 – Bohm and Ahronov proof of entanglement in 1950 Wu experiment

1959 – Ahronov-Bohm effect of magnetic vector potential

1960 – Klauder: Coherent states

1963 – Coherent states, R. J. Glauber: Phys. Rev. 130 , 2529 (1963)

1963 – Coherent states, E. C. G. Sudarshan: Phys. Rev. Lett. 10, 277 (1963)

1964 – J. S. Bell: Bell inequalities [8]

1964 – Mandel professorship at Rochester

1967 – Interference at single photon level, R. F. Pfleegor, L. Mandel: [9]

1967 – M. O. Scully, W.E. Lamb: Phys. Rev. 159 , 208 (1967) Quantum theory of laser

1967 – Parametric converter (Mollow and Glauber) [10]

1967 – Kocher and Commins calcium 2-photon cascade

1969 – Quantum theory of laser, M. Lax, W.H. Louisell: Phys. Rev. 185 , 568 (1969)

1969 – CHSH inequality [11]

1972 – First test of Bell’s inequalities (Freedman and Clauser)

1975 – Carmichel and Walls predicted light in resonance fluorescence from a two-level atom would display photon anti-bunching (1976)

1977 – Photon antibunching in resonance fluorescence. H. J. Kimble, M. Dagenais and L. Mandel [12]

1978 – Kip Thorne quantum non-demolition (QND)

1979 – Hollenhorst squeezing for gravitational wave detection: names squeezing

1982 – Apect Experimental Bell experiments, [13]

1985 – Dick Slusher experimental squeezing

1985 – Deutsch quantum algorithm

1986 – Photon anti-bunching at a beamsplitter, P. Grangier, G. Roger, A. Aspect: [14]

1986 – Kimble squeezing in parametric down-conversion

1986 – C. K. Hong, L. Mandel: Phys. Rev. Lett. 56 , 58 (1986) one-photon localization

1987 – Two-photon interference (Ghosh and Mandel) [15]

1987 – HOM effect [16]

1987 – Photon squeezing, P. Grangier, R. E. Slusher, B. Yurke, A. La Porta: [17]

1987 – Grangier and Slusher, squeezed light interferometer

1988 – 2-photon Bell violation: Z. Y. Ou, L. Mandel: Phys. Rev. Lett. 61 , 50 (1988)

1988 – Brassard Quantum cryptography

1989 – Franson proposes two-photon interference in k-number (?)

1990 – Two-photon interference in k-number (Kwiat and Chiao)

1990 – Two-photon interference (Ou, Zhou, Wang and Mandel)

1993 – Quantum teleportation proposal (Bennett)

1994 – Teleportation of quantum states (Vaidman)

1994 – Shor factoring algorithm

1995 – Down-conversion for polarization: Kwiat and Zeilinger (1995)

1997 – Experimental quantum teleportation (Bouwmeester)

1997 – Experimental quantum teleportation (Bosci)

1998 – Unconditional quantum teleportation (every state) (Furusawa)

2001 – Quantum computing with linear optics (Knill, Laflamme, Milburn)

2013 – LIGO design proposal with squeezed light (Aasi)

2019 – Squeezing upgrade on LIGO (Tse)

2020 – Quantum computational advantage (Zhong)

10. The Quantum Advantage

There is almost no technical advantage better than having exponential resources at hand. The exponential resources of quantum interference provide that advantage to quantum computing which is poised to usher in a new era of quantum information science and technology.

Topics: Interferometric Computing. David Deutsch. Quantum Algorithm. Peter Shor. Prime Factorization. Quantum Logic Gates. Linear Optical Quantum Computing. Boson Sampling. Quantum Computational Advantage.

1980 – Paul Benioff describes possibility of quantum computer

1981 – Feynman simulating physics with computers

1985 – Deutsch quantum Turing machine [18]

1987 – Quantum properties of beam splitters

1992 – Deutsch Josza algorithm is exponential faster than classical

1993 – Quantum teleportation described

1994 – Shor factoring algorithm [19]

1994 – First quantum computing conference

1995 – Shor error correction

1995 – Universal gates

1996 – Grover search algorithm

1998 – First demonstration of quantum error correction

1999 – Nakamura and Tsai superconducting qubits

2001 – Superconducting nanowire photon detectors

2001 – Linear optics quantum computing (KLM)

2001 – One-way quantum computer

2003 – All-optical quantum gate in a quantum dot (Li)

2003 – All-optical quantum CNOT gate (O’Brien)

2003 – Decoherence and einselection (Zurek)

2004 – Teleportation across the Danube

2005 – Experimental quantum one-way computing (Walther)

2007 – Teleportation across 114 km (Canary Islands)

2008 – Quantum discord computing

2011 – D-Wave Systems offers commercial quantum computer

2011 – Aaronson boson sampling

2012 – 1QB Information Technnologies, first quantum software company

2013 – Experimental demonstrations of boson sampling

2014 – Teleportation on a chip

2015 – Universal linear optical quantum computing (Carolan)

2017 – Teleportation to a satellite

2019 – Generation of a 2D cluster state (Larsen)

2019 – Quantum supremacy [20]

2020 – Quantum optical advantage [21]

2021 – Programmable quantum photonic chip

References:

[1] Annalen Der Physik 4(3): 553-563.

[2] Annalen Der Physik 17(6): 132-148.

[3] Physikalische Zeitschrift 10: 185-193.

[4] Proc. Cam. Phil. Soc. Math. Phys. Sci. 15 , 114 (1909)

[5] Physical Review. 21 (5): 483–502.

[6] Proceedings of the Royal Society of London Series a-Containing Papers of a Mathematical and Physical Character 114(767): 243-265.

[7] D. Bohm, “A suggested interpretation of the quantum theory in terms of hidden variables .1,” Physical Review, vol. 85, no. 2, pp. 166-179, (1952)

[8] Physics 1 , 195 (1964); Rev. Mod. Phys. 38 , 447 (1966)

[9] Phys. Rev. 159 , 1084 (1967)

[10] B. R. Mollow, R. J. Glauber: Phys. Rev. 160, 1097 (1967); 162, 1256 (1967)

[11] J. F. Clauser, M. A. Horne, A. Shimony, and R. A. Holt, ” Proposed experiment to test local hidden-variable theories,” Physical Review Letters, vol. 23, no. 15, pp. 880-&, (1969)

[12] (1977) Phys. Rev. Lett. 39, 691-5

[13] A. Aspect, P. Grangier, G. Roger: Phys. Rev. Lett. 49 , 91 (1982). A. Aspect, J. Dalibard, G. Roger: Phys. Rev. Lett. 49 , 1804 (1982)

[14] Europhys. Lett. 1 , 173 (1986)

[15] R. Ghosh and L. Mandel, “Observation of nonclassical effects in the interference of 2 photons,” Physical Review Letters, vol. 59, no. 17, pp. 1903-1905, Oct (1987)

[16] C. K. Hong, Z. Y. Ou, and L. Mandel, “Measurement of subpicosecond time intervals between 2 photons by interference,” Physical Review Letters, vol. 59, no. 18, pp. 2044-2046, Nov (1987)

[17] Phys. Rev. Lett 59, 2153 (1987)

[18] D. Deutsch, “QUANTUM-THEORY, THE CHURCH-TURING PRINCIPLE AND THE UNIVERSAL QUANTUM COMPUTER,” Proceedings of the Royal Society of London Series a-Mathematical Physical and Engineering Sciences, vol. 400, no. 1818, pp. 97-117, (1985)

[19] P. W. Shor, “ALGORITHMS FOR QUANTUM COMPUTATION – DISCRETE LOGARITHMS AND FACTORING,” in 35th Annual Symposium on Foundations of Computer Science, Proceedings, S. Goldwasser Ed., (Annual Symposium on Foundations of Computer Science, 1994, pp. 124-134.

[20] F. Arute et al., “Quantum supremacy using a programmable superconducting processor,” Nature, vol. 574, no. 7779, pp. 505-+, Oct 24 (2019)

[21] H.-S. Zhong et al., “Quantum computational advantage using photons,” Science, vol. 370, no. 6523, p. 1460, (2020)

Relativistic Velocity Addition: Einstein’s Crucial Insight

The first step on the road to Einstein’s relativity was taken a hundred years earlier by an ironic rebel of physics—Augustin Fresnel. His radical (at the time) wave theory of light was so successful, especially the proof that it must be composed of transverse waves, that he was single-handedly responsible for creating the irksome luminiferous aether that would haunt physicists for the next century. It was only when Einstein combined the work of Fresnel with that of Hippolyte Fizeau that the aether was ultimately banished.

Augustin Fresnel: Ironic Rebel of Physics

Augustin Fresnel was an odd genius who struggled to find his place in the technical hierarchies of France. After graduating from the Ecole Polytechnique, Fresnel was assigned a mindless job overseeing the building of roads and bridges in the boondocks of France—work he hated. To keep himself from going mad, he toyed with physics in his spare time, and he stumbled on inconsistencies in Newton’s particulate theory of light that Laplace, a leader of the French scientific community, embraced as if it were revealed truth .

The final irony is that Einstein used Fresnel’s theoretical coefficient and Fizeau’s measurements—that had introduced aether drag in the first place—to show that there was no aether.

Fresnel rebelled, realizing that effects of diffraction could be explained if light were made of waves. He wrote up an initial outline of his new wave theory of light, but he could get no one to listen, until Francois Arago heard of it. Arago was having his own doubts about the particle theory of light based on his experiments on stellar aberration.

*Augustin Fresnel and Francois Arago (circa 1818*)

Stellar Aberration and the Fresnel Drag Coefficient

Stellar aberration had been explained by James Bradley in 1729 as the effect of the motion of the Earth relative to the motion of light “particles” coming from a star. The Earth’s motion made it look like the star was tilted at a very small angle (see my previous blog). That explanation had worked fine for nearly a hundred years, but then around 1810 Francois Arago at the Paris Observatory made extremely precise measurements of stellar aberration while placing finely ground glass prisms in front of his telescope. According to Snell’s law of refraction, which depended on the velocity of the light particles, the refraction angle should have been different at different times of the year when the Earth was moving one way or another relative to the speed of the light particles. But to high precision the effect was absent. Arago began to question the particle theory of light. When he heard about Fresnel’s work on the wave theory, he arranged a meeting, encouraging Fresnel to continue his work.

But at just this moment, in March of 1815, Napoleon returned from exile in Elba and began his march on Paris with a swelling army of soldiers who flocked to him. Fresnel rebelled again, joining a royalist militia to oppose Napoleon’s return. Napoleon won, but so did Fresnel, who was ironically placed under house arrest, which was like heaven to him. It freed him from building roads and bridges, giving him free time to do optics experiments in his mother’s house to support his growing theoretical work on the wave nature of light.

Arago convinced the authorities to allow Fresnel to come to Paris, where the two began experiments on diffraction and interference. By using polarizers to control the polarization of the interfering light paths, they concluded that light must be composed of transverse waves.

This brilliant insight was then followed by one of the great tragedies of science—waves needed a medium within which to propagate, so Fresnel conceived of the luminiferous aether to support it. Worse, the transverse properties of light required the aether to have a form of crystalline stiffness.

How could moving objects, like the Earth orbiting the sun, travel through such an aether without resistance? This was a serious problem for physics. One solution was that the aether was entrained by matter, so that as matter moved, the aether was dragged along with it. That solved the resistance problem, but it raised others, because it couldn’t explain Arago’s refraction measurements of aberration.

Fresnel realized that Arago’s null results could be explained if aether was only partially dragged along by matter. For instance, in the glass prisms used by Arago, the fraction of the aether being dragged along by the moving glass versus at rest would depend on the refractive index n of the glass. The speed of light in moving glass would then be

where c is the speed of light through stationary aether, v_g is the speed of the glass prism through the stationary aether, and V is the speed of light in the moving glass. The first term in the expression is the ordinary definition of the speed of light in stationary matter with the refractive index. The second term is called the Fresnel drag coefficient which he communicated to Arago in a letter in 1818. Even at the high speed of the Earth moving around the sun, this second term is a correction of only about one part in ten thousand. It explained Arago’s null results for stellar aberration, but it was not possible to measure it directly in the laboratory at that time.

Fizeau’s Moving Water Experiment

Hippolyte Fizeau has the distinction of being the first to measure the speed of light directly in an Earth-bound experiment. All previous measurements had been astronomical. The story of his ingenious use of a chopper wheel and long-distance reflecting mirrors placed across the city of Paris in 1849 can be found in Chapter 3 of Interference. However, two years later he completed an experiment that few at the time noticed but which had a much more profound impact on the history of physics.

In 1851, Fizeau modified an Arago interferometer to pass two interfering light beams along pipes of moving water. The goal of the experiment was to measure the aether drag coefficient directly and to test Fresnel’s theory of partial aether drag. The interferometer allowed Fizeau to measure the speed of light in moving water relative to the speed of light in stationary water. The results of the experiment confirmed Fresnel’s drag coefficient to high accuracy, which seemed to confirm the partial drag of aether by moving matter.

*Fizeau’s 1851 measurement of the speed of light in water using a modified Arago interferometer.* (Reprinted from Chapter 2: Interference.)

This result stood for thirty years, presenting its own challenges for physicist exploring theories of the aether. The sophistication of interferometry improved over that time, and in 1881 Albert Michelson used his newly-invented interferometer to measure the speed of the Earth through the aether. He performed the experiment in the Potsdam Observatory outside Berlin, Germany, and found the opposite result of complete aether drag, contradicting Fizeau’s experiment. Later, after he began collaborating with Edwin Morley at Case and Western Reserve Colleges in Cleveland, Ohio, the two repeated Fizeau’s experiment to even better precision, finding once again Fresnel’s drag coefficient, followed by their own experiment, known now as “the Michelson-Morley Experiment” in 1887, that found no effect of the Earth’s movement through the aether.

The two experiments—Fizeau’s measurement of the Fresnel drag coefficient, and Michelson’s null measurement of the Earth’s motion—were in direct contradiction with each other. Based on the theory of the aether, they could not both be true.

But where to go from there? For the next 15 years, there were numerous attempts to put bandages on the aether theory, from Fitzgerald’s contraction to Lorenz’ transformations, but it all seemed like kludges built on top of kludges. None of it was elegant—until Einstein had his crucial insight.

Einstein’s Insight

While all the other top physicists at the time were trying to save the aether, taking its real existence as a fact of Nature to be reconciled with experiment, Einstein took the opposite approach—he assumed that the aether did not exist and began looking for what the experimental consequences would be.

From the days of Galileo, it was known that measured speeds depended on the frame of reference. This is why a knife dropped by a sailor climbing the mast of a moving ship strikes at the base of the mast, falling in a straight line in the sailor’s frame of reference, but an observer on the shore sees the knife making an arc—velocities of relative motion must add. But physicists had over-generalized this result and tried to apply it to light—Arago, Fresnel, Fizeau, Michelson, Lorenz—they were all locked in a mindset.

Einstein stepped outside that mindset and asked what would happen if all relatively moving observers measured the same value for the speed of light, regardless of their relative motion. It was just a little algebra to find that the way to add the speed of light c to the speed of a moving reference frame v_ref was

where the numerator was the usual Galilean relativity velocity addition, and the denominator was required to enforce the constancy of observed light speeds. Therefore, adding the speed of light to the speed of a moving reference frame gives back simply the speed of light.

Generalizing this equation for general velocity addition between moving frames gives

where u is now the speed of some moving object being added the the speed of a reference frame, and v_obs is the “net” speed observed by some “external” observer . This is Einstein’s famous equation for relativistic velocity addition (see pg. 12 of the English translation). It ensures that all observers with differently moving frames all measure the same speed of light, while also predicting that no velocities for objects can ever exceed the speed of light.

This last fact is a consequence, not an assumption, as can be seen by letting the reference speed v_ref increase towards the speed of light so that v_ref ≈ c, then

so that the speed of an object launched in the forward direction from a reference frame moving near the speed of light is still observed to be no faster than the speed of light

All of this, so far, is theoretical. Einstein then looked to find some experimental verification of his new theory of relativistic velocity addition, and he thought of the Fizeau experimental measurement of the speed of light in moving water. Applying his new velocity addition formula to the Fizeau experiment, he set v_ref = v_water and u = c/n and found

The second term in the denominator is much smaller that unity and is expanded in a Taylor’s expansion

The last line is exactly the Fresnel drag coefficient!

Therefore, Fizeau, half a century before, in 1851, had already provided experimental verification of Einstein’s new theory for relativistic velocity addition! It wasn’t aether drag at all—it was relativistic velocity addition.

From this point onward, Einstein followed consequence after inexorable consequence, constructing what is now called his theory of Special Relativity, complete with relativistic transformations of time and space and energy and matter—all following from a simple postulate of the constancy of the speed of light and the prescription for the addition of velocities.

The final irony is that Einstein used Fresnel’s theoretical coefficient and Fizeau’s measurements, that had established aether drag in the first place, as the proof he needed to show that there was no aether. It was all just how you looked at it.

The Aberration of Starlight: Relativity’s Crucible

The Earth races around the sun with remarkable speed—at over one hundred thousand kilometers per hour on its yearly track. This is about 0.01% of the speed of light—a small but non-negligible amount for which careful measurement might show the very first evidence of relativistic effects. How big is this effect and how do you measure it? One answer is the aberration of starlight, which is the slight deviation in the apparent position of stars caused by the linear speed of the Earth around the sun.

This is not parallax, which is caused the the changing position of the Earth around the sun. Ever since Copernicus, astronomers had been searching for parallax, which would give some indication how far away stars were. It was an important question, because the answer would say something about how big the universe was. But in the process of looking for parallax, astronomers found something else, something about 50 times bigger—aberration.

Aberration is the effect of the transverse speed of the Earth added to the speed of light coming from a star. For instance, this effect on the apparent location of stars in the sky is a simple calculation of the arctangent of 0.01%, which is an angle of about 20 seconds of arc, or about 40 seconds when comparing two angles 6 months apart. This was a bit bigger than the accuracy of astronomical measurements at the time when Jean Picard travelled from Paris to Denmark in 1671 to visit the ruins of the old observatory of Tycho Brahe at Uranibourg.

Fig. 1 Stellar parallax is the change in apparent positions of a star caused by the change in the Earth’s position as it orbits the sun. If the change in angle (θ) could be measured, then based on Newton’s theory of gravitation that gives the radius of the Earth’s orbit (R), the distance to the star (L) could be found.

Jean Picard at Uranibourg

*Fig. 2 A view of Tycho Brahe’s Uranibourg astronomical observatory in Hven, Denmark. Tycho had to abandon it near the end of his life when a new king thought he was performing witchcraft.*

Jean Picard went to Uranibourg originally in 1671, and during subsequent years, to measure the eclipses of the moons of Jupiter to determine longitude at sea—an idea first proposed by Galileo. When visiting Copenhagen, before heading out to the old observatory, Picard secured the services of an as yet unknown astronomer by the name of Ole Rømer. While at Uranibourg, Picard and Rømer made their required measurements of the eclipses of the moons of Jupiter, but with extra observation hours, Picard also made measurements of the positions of selected stars, such as Polaris, the North Star. His very precise measurements allowed him to track a tiny yearly shift, an aberration, in position by about 40 seconds of arc. At the time (before Rømer’s great insight about the finite speed of light—see Chapter 1 of Interference (Oxford, 2023)), the speed of light was thought to be either infinite or unmeasurably fast, so Picard thought that this shift was the long-sought effect of stellar parallax that would serve as a way to measure the distance to the stars. However, the direction of the shift of Polaris was completely wrong if it were caused by parallax, and Picard’s stellar aberration remained a mystery.

*Fig. 3 Jean Picard (left) and his modern name-sake (right).*

Samuel Molyneux and Murder in Kew

In 1725, the amateur Irish astronomer Samuel Molyneux (1689 – 1828) decided that the tools of astronomy had improved to the point that the question of parallax could be answered. He enlisted the help of an instrument maker outside London to install a 24-foot zenith sector (a telescope that points vertically upwards) at his home in Kew. Molyneux was an independently wealthy politician (he had married the first daughter of the second Earl of Essex) who sat in the British House of Commons, and he was also secretary to the Prince of Wales (the future George II). Because his political activities made demands on his time, he looked for assistance with his observations and invited James Bradley (1693 – 1762), the newly installed Savilian Professor of Astronomy at Oxford University, to join him in his search.

James Bradley was a rising star in the scientific circles of England. He came from a modest background but had the good fortune that his mother’s brother, James Pound, was a noted amateur astronomer who had set up a small observatory at his rectory in Wanstead. Bradley showed an early interest in astronomy, and Pound encouraged him, helping with the finances of his education that took him to degrees at Baliol College at Oxford. Even more fortunate was the fact that Pound’s close friend was the Astronomer Royal Edmund Halley, who also took a special interest in Bradley. With Halley’s encouragement, Bradley made important measurements of Mars and several nebulae, demonstrating an ability to work with great accuracy. Halley was impressed and nominated Bradley to the Royal Society in 1718, telling everyone that Bradley was destined to be one of the great astronomers of his time.

Molyneux must have sensed immediately that he had chosen wisely by selecting Bradley to help him with the parallax measurements. Bradley was capable of exceedingly precise work and was fluent mathematically with the geometric complexities of celestial orbits. Fastening the large zenith sector to the chimney of the house gave the apparatus great stability, and in December of 1725 they commenced observations of Gamma Draconis as it passed directly overhead. Because of the accuracy of the sector, they quickly observed a deviation in the star’s position, but the deviation was in the wrong direction, just as Picard had observed. They continued to make observations over two years, obtaining a detailed map of a yearly wobble in the star’s position as it changed angle by 40 seconds of arc (about one percent of a degree) over six months.

When Molyneux was appointed Lord of the Admiralty in 1727, as well as becoming a member of the Irish Parliament (representing Dublin University), he had little time to continue with the observations of Gamma Draconis. He helped Bradley set up a Zenith sector telescope at Bradley’s uncle’s observatory in Wanstead that had a wider field of view to observe more stars, and then he left the project to his friend. A few months later, before either he or Bradley had understood the cause of the stellar aberration, Molyneux collapsed while in the House of Commons and was carried back to his house. One of Molyneux’s many friends was the court anatomist Nathaniel St. André who attended to him over the next several days as he declined and died. St. André was already notorious for roles he had played in several public hoaxes, and on the night of his friend’s death, before the body had grown cold, he eloped with Molyneux’s wife, raising accusations of murder (that could never be proven).

James Bradley and the Light Wind

Over the following year, Bradley observed aberrations in several stars, all of them displaying the same yearly wobble of about 40 seconds of arc. This common behavior of numerous stars demanded a common explanation, something they all shared. It is said that the answer came to Bradley while he was boating on the Thames. The story may be apocryphal, but he apparently noticed the banner fluttering downwind at the top of the mast, and after the boat came about, the banner pointed in a new direction. The wind direction itself had not altered, but the motion of the boat relative to the wind had changed. Light at that time was considered to be made of a flux of corpuscles, like a gentle wind of particles. As the Earth orbited the Sun, its motion relative to this wind would change periodically with the seasons, and the apparent direction of the star would shift a little as a result.

Fig. 5 Principle of stellar aberration. On the left is the rest frame of the star positioned directly overhead as a moving telescope tube must be slightly tilted at an angle (equal to the arctangent of the ratio of the Earth’s speed to the speed of light–greatly exaggerated in the figure) to allow the light to pass through it. On the right is the rest frame of the telescope in which the angular position of the star appears shifted.

Bradley shared his observations and his explanation in a letter to Halley that was read before the Royal Society in January of 1729. Based on his observations, he calculated the speed of light to be about ten thousand times faster than the speed of the Earth in its orbit around the Sun. At that speed, it should take light eight minutes and twelve seconds to travel from the Sun to the Earth (the actual number is eight minutes and 19 seconds). This number was accurate to within a percent of the true value compared with the estimates made by Huygens from the eclipses of the moons of Jupiter that were in error by 27 percent. In addition, because he was unable to discern any effect of parallax in the stellar motions, Bradley was able to place a limit on how far the distant stars must be, more than 100,000 times farther the distance of the Earth from the Sun, which was much farther away than any had previously expected. In January of 1729 the size of the universe suddenly jumped to an incomprehensibly large scale.

Bradley’s explanation of the aberration of starlight was simple and matched observations with good quantitative accuracy. The particle nature of light made it like a wind, or a current, and the motion of the Earth was just a case of Galilean relativity that any freshman physics student can calculate. At first there seemed to be no controversy or difficulties with this interpretation. However, an obscure paper published in 1784 by an obscure English natural philosopher named John Michell (the first person to conceive of a “dark star”) opened a Pandora’s box that launched the crisis of the luminiferous ether and the eventual triumph of Einstein’s theory of Relativity (see Chapter 3 of Interference (Oxford, 2023)), .

September 4, 2023September 25, 2023 by David D. Nolte

Orion’s Dog: The Serious Science of Sirius

The constellation Orion strides high across the heavens on cold crisp winter nights in the North, followed at his heel by his constant companion, Canis Major, the Great Dog. Blazing blue from the Dog’s proud chest is the star Sirius, the Dog Star, the brightest star in the night sky. Although it is only the seventh closest star system to our sun, the other six systems host dimmer dwarf stars. Sirius, on the other hand, is a young bright star burning blue in the night. It is an infant star, really, only as old as 5% the age of our sun, coming into being when Dinosaurs walked our planet.

The Sirius star system is a microcosm of mankind’s struggle to understand the Universe. Because it is close and bright, it has become the de facto bench-test for new theories of astrophysics as well as for new astronomical imaging technologies. It has played this role from the earliest days of history, when it was an element of religion rather than of science, down to the modern age as it continues to test and challenge new ideas about quantum matter and extreme physics.

Sirius Through the Ages

To the ancient Egyptians, Sirius was the star Sopdet, the welcome herald of the flooding of the Nile when it rose in the early morning sky of autumn. The star was associated with Isis of the cow constellation Hathor (Canis Major) following closely behind Osiris (Orion). The importance of the annual floods for the well-being of the ancient culture cannot be underestimated, and entire religions full of symbolic significance revolved around the heliacal rising of Sirius.

To the Greeks, Sirius was always Sirius, although no one even as far back as Hesiod in the 7^th century BC could recall where it got its name. It was the dog star, as it was also to the Persians and the Hindus who called it Tishtrya and Tishya, respectively. The loss of the initial “T” of these related Indo-European languages is a historical sound shift in relation to “S”, indicating that the name of the star dates back at least as far as the divergence of the Indo-European languages around the fourth millennium BC. (Even more intriguing is the same association of Sirius with dogs and wolves by the ancient Chinese and by Alaskan Innuits, as well as by many American Indian tribes, suggesting that the cultural significance of the star, if not its name, may have propagated across Asia and the Bering Strait as far back as the end of the last Ice Age.) As the brightest star of the sky, this speaks to an enduring significance for Sirius, dating back to the beginning of human awareness of our place in nature. No culture was unaware of this astronomical companion to the Sun and Moon and Planets.

The Greeks, too, saw Sirius as a harbinger, not for life-giving floods, but rather of the sweltering heat of late summer. Homer, in the Iliad, famously wrote:

And aging Priam was the first to see him

sparkling on the plain, bright as that star

in autumn rising, whose unclouded rays

shine out amid a throng of stars at dusk—

the one they call Orion's dog, most brilliant,

yes, but baleful as a sign: it brings

great fever to frail men. So pure and bright

the bronze gear blazed upon him as he ran.

The Romans expanded on this view, describing “the dog days of summer”, which is a phrase that echoes till today as we wait for the coming coolness of autumn days.

The Heavens Move

The irony of the Copernican system of the universe, when it was proposed in 1543 by Nicolaus Copernicus, is that it took stars that moved persistently through the heavens and fixed them in the sky, unmovable. The “fixed stars” became the accepted norm for several centuries, until the peripatetic Edmund Halley (1656 – 1742) wondered if the stars really did not move. From Newton’s new work on celestial dynamics (the famous Principia, which Halley generously paid out of his own pocket to have published not only because of his friendship with Newton, but because Halley believed it to be a monumental work that needed to be widely known), it was understood that gravitational effects would act on the stars and should cause them to move.

In 1710 Halley began studying the accurate star-location records of Ptolemy from one and a half millennia earlier and compared them with what he could see in the night sky. He realized that the star Sirius had shifted in the sky by an angular distance equivalent to the diameter of the moon. Other bright stars, like Arcturus and Procyon, also showed discrepancies from Ptolemy. On the other hand, dimmer stars, that Halley reasoned were farther away, showed no discernible shifts in 1500 years. At a time when stellar parallax, the apparent shift in star locations caused by the movement of the Earth, had not yet been detected, Halley had found an alternative way to get at least some ranked distances to the stars based on their proper motion through the universe. Closer stars to the Earth would show larger angular displacements over 1500 years than stars farther away. By being the closest bright star to Earth, Sirius had become a testbed for observations and theories of the motions of stars. With the confidence of the confirmation of the nearness of Sirius to the Earth, Jacques Cassini claimed in 1714 to have measured the parallax of Sirius, but Halley refuted this claim in 1720. Parallax would remain elusive for another hundred years to come.

The Sound of Sirius

Of all the discoveries that emerged from nineteenth century physics—Young’s fringes, Biot-Savart law, Fresnel lens, Carnot cycle, Faraday effect, Maxwell’s equations, Michelson interferometer—only one is heard daily—the Doppler effect [1]. Doppler’s name is invoked every time you turn on the evening news to watch Doppler weather radar. Doppler’s effect is experienced as you wait by the side of the road for a car to pass by or a jet to fly overhead. Einstein may have the most famous name in physics, but Doppler’s is certainly the most commonly used.

Although experimental support for the acoustic Doppler effect accumulated quickly, corresponding demonstrations of the optical Doppler effect were slow to emerge. The breakthrough in the optical Doppler effect was made by William Huggins (1824-1910). Huggins was an early pioneer in astronomical spectroscopy and was famous for having discovered that some bright nebulae consist of atomic gases (planetary nebula in our own galaxy) while others (later recognized as distant galaxies) consist of unresolved emitting stars. Huggins was intrigued by the possibility of using the optical Doppler effect to measure the speed of stars, and he corresponded with James Clerk Maxwell (1831-1879) to confirm the soundness of Doppler’s arguments, which Maxwell corroborated using his new electromagnetic theory. With the resulting confidence, Huggins turned his attention to the brightest star in the heavens, Sirius, and on May 14, 1868, he read a paper to the Royal Society of London claiming an observation of Doppler shifts in the spectral lines of the star Sirius consistent with a speed of about 50 km/sec [2].

*Fig. Doppler spectroscopy of stellar absorption lines caused by the relative motion of the star (in this illustration the orbiting exoplanet is causing the star to wobble.)*

The importance of Huggins’ report on the Doppler effect from Sirius was more psychological than scientifically accurate, because it convinced the scientific community that the optical Doppler effect existed. Around this time the German astronomer Hermann Carl Vogel (1841 – 1907) of the Potsdam Observatory began working with a new spectrograph designed by Johann Zöllner from Leipzig [3] to improve the measurements of the radial velocity of stars (the speed along the line of sight). He was aware that the many values quoted by Huggins and others for stellar velocities were nearly the same as the uncertainties in their measurements. Vogel installed photographic capabilities in the telescope and spectrograph at the Potsdam Observatory [4] in 1887 and began making observations of Doppler line shifts in stars through 1890. He published an initial progress report in 1891, and then a definitive paper in 1892 that provided the first accurate stellar radial velocities [5]. Fifty years after Doppler read his paper to the Royal Bohemian Society of Science (in 1842 to a paltry crowd of only a few scientists), the Doppler effect had become an established workhorse of quantitative astrophysics. A laboratory demonstration of the optical Doppler effect was finally achieved in 1901 by Aristarkh Belopolsky (1854-1934), a Russian astronomer, by constructing a device with a narrow-linewidth light source and rapidly rotating mirrors [6].

White Dwarf

While measuring the position of Sirius to unprecedented precision, the German astronomer Friedrich Wilhelm Bessel (1784 – 1846) noticed a slow shift in its position. (This is the same Bessel as “Bessel function” fame, although the functions were originally developed by Daniel Bernoulli and Bessel later generalized them.) Bessel deduced that Sirius must have an unseen companion with an orbital of around 50 years. This companion was discovered by accident in 1862 during a test run of a new lens manufactured by the Clark&Sons glass manufacturing company prior to delivery to Northwestern University in Chicago. (The lens was originally ordered by the University of Mississippi in 1860, but after the Civil War broke out, the Massachusetts-based Clark company put it up for bid. Harvard wanted it, but Northwestern got it.) Sirius itself was redesignated Sirius A, while this new star was designated Sirius B (and sometimes called “The Pup”).

The Pup’s spectrum was measured in 1915 by Walter Adams (1876 – 1956) which put it in the newly-formed class of “white dwarf” stars that were very small but, unlike other types of dwarf stars, they had very hot (white) spectra. The deflection of the orbit of Sirius A allowed its mass to be estimated at about one solar mass, which was normal for a dwarf star. Furthermore, its brightness and surface temperature allowed its density to be estimated, but here an incredible number came out: the density of Sirius B was about 30,000 times greater than the density of the sun! Astronomers at the time thought that this was impossible, and Arthur Eddington, who was the expert in star formation, called it “nonsense”. This nonsense withstood all attempts to explain it for over a decade.

In 1926, R. H. Fowler (1889 – 1944) at Cambridge University in England applied the newly-developed theory of quantum mechanics and the Pauli exclusion principle to the problem of such ultra-dense matter. He found that the Fermi sea of electrons provided a type of pressure, called degeneracy pressure, that counteracted the gravitational pressure that threatened to collapse the star under its own weight. Several years later, Subrahmanyan Chandrasekhar calculated the upper limit for white dwarfs using relativistic effects and accurate density profiles and found that a white dwarf with a mass greater than about 1.5 times the mass of the sun would no longer be supported by the electron degeneracy pressure and would suffer gravitational collapse. At the time, the question of what it would collapse to was unknown, although it was later understood that it would collapse to a neutron star. Sirius B, at about one solar mass, is well within the stable range of white dwarfs.

But this was not the end of the story for Sirius B [7]. At around the time that Adams was measuring the spectrum of the white dwarf, Einstein was predicting that light emerging from a dense star would have its wavelengths gravitationally redshifted relative to its usual wavelength. This was one of the three classic tests he proposed for his new theory of General Relativity. (1 – The precession of the perihelion of Mercury. 2 – The deflection of light by gravity. 3 – The gravitational redshift of photons rising out of a gravity well.) Adams announced in 1925 (after the deflection of light by gravity had been confirmed by Eddington in 1919) that he had measured the gravitational redshift. Unfortunately, it was later surmised that he had not measured the gravitational effect but had actually measured Doppler-shifted spectra because of the rotational motion of the star. The true gravitational redshift of Sirius B was finally measured in 1971, although the redshift of another white dwarf, 40 Eridani B, had already been measured in 1954.

Static Interference

The quantum nature of light is an elusive quality that requires second-order experiments of intensity fluctuations to elucidate them, rather than using average values of intensity. But even in second-order experiments, the manifestations of quantum phenomenon are still subtle, as evidenced by an intense controversy that was launched by optical experiments performed in the 1950’s by a radio astronomer, Robert Hanbury Brown (1916 – 2002). (For the full story, see Chapter 4 in my book Interference from Oxford (2023) [8]).

Hanbury Brown (he never went by his first name) was born in Aruvankandu, India, the son of a British army officer. He never seemed destined for great things, receiving an unremarkable education that led to a degree in radio engineering from a technical college in 1935. He hoped to get a PhD in radio technology, and he even received a scholarship to study at Imperial College in London, when he was urged by the rector of the university, Sir Henry Tizard, to give up his plans and join an effort to develop defensive radar against a growing threat from Nazi Germany as it aggressively rearmed after abandoning the punitive Versailles Treaty. Hanbury Brown began the most exciting and unnerving five years of his life, right in the middle of the early development of radar defense, leading up to the crucial role it played in the Battle of Britain in 1940 and the Blitz from 1940 to 1941. Partly due to the success of radar, Hitler halted night-time raids in the Spring of 1941, and England escaped invasion.

In 1949, fourteen years after he had originally planned to start his PhD, Hanbury Brown enrolled at the relatively ripe age of 33 at the University of Manchester. Because of his background in radar, his faculty advisor told him to look into the new field of radio astronomy that was just getting started, and Manchester was a major player because it administrated the Jodrell Bank Observatory, which was one of the first and largest radio astronomy observatories in the World. Hanbury Brown was soon applying all he had learned about radar transmitters and receivers to the new field, focusing particularly on aspects of radio interferometry after Martin Ryle (1918 – 1984) at Cambridge with Derek Vonberg (1921 – 2015) developed the first radio interferometer to measure the angular size of the sun [9] and of radio sources on the Sun’s surface that were related to sunspots [10]. Despite the success of their measurements, their small interferometer was unable to measure the size of other astronomical sources. From Michelson’s formula for stellar interferometry, longer baselines between two separated receivers would be required to measure smaller angular sizes. For his PhD project, Hanbury Brown was given the task of designing a radio interferometer to resolve the two strongest radio sources in the sky, Cygnus A and Cassiopeia A, whose angular sizes were unknown. As he started the project, he was confronted with the problem of distributing a stable reference signal to receivers that might be very far apart, maybe even thousands of kilometers, a problem that had no easy solution.

After grappling with this technical problem for months without success, late one night in 1949 Hanbury Brown had an epiphany [11], wondering what would happen if the two separate radio antennas measured only intensities rather than fields. The intensity in a radio telescope fluctuates in time like random noise. If that random noise were measured at two separated receivers while trained on a common source, would those noise patterns look the same? After a few days considering this question, he convinced himself that the noise would indeed share common features, and the degree to which the two noise traces were similar should depend on the size of the source and the distance between the two receivers, just like Michelson’s fringe visibility. But his arguments were back-of-the-envelope, so he set out to find someone with the mathematical skills to do it more rigorously. He found Richard Twiss.

Richard Quentin Twiss (1920 – 2005), like Hanbury Brown, was born in India to British parents but had followed a more prestigious educational path, taking the Mathematical Tripos exam at Cambridge in 1941 and receiving his PhD from MIT in the United States in 1949. He had just returned to England, joining the research division of the armed services located north of London, when he received a call from Hanbury Brown at the Jodrell Bank radio astronomy laboratory in Manchester. Twiss travelled to meet Hanbury Brown in Manchester, who put him up in his flat in the neighboring town of Wilmslow. The two set up the mathematical assumptions behind the new “intensity interferometer” and worked late into the night. When Hanbury Brown finally went to bed, Twiss was still figuring the numbers. The next morning, the tall and lanky Twiss appeared in his silk dressing gown in the kitchen and told Hanbury Brown, “This idea of yours is no good, it doesn’t work”[12]—it would never be strong enough to detect the intensity from stars. However, after haggling over the details of some of the integrals, Hanbury Brown, and then finally Twiss, became convinced that the effect was real. Rather than fringe visibility, it was the correlation coefficient between two noise signals that would depend on the joint sizes of the source and receiver in a way that captured the same information as Michelson’s first-order fringe visibility. But because no coherent reference wave was needed for interferometric mixing, this new approach could be carried out across very large baseline distances.

After demonstrating the effect on astronomical radio sources, Hanbury Brown and Twiss took the next obvious step: optical stellar intensity interferometry. Their work had shown that photon noise correlations were analogous to Michelson fringe visibility, so the stellar intensity interferometer was expected to work similarly to the Michelson stellar interferometer—but with better stability over much longer baselines because it did not need a reference. An additional advantage was the simple light collecting requirements. Rather than needing a pair of massively expensive telescopes for high-resolution imaging, the intensity interferometer only needed to point two simple light collectors in a common direction. For this purpose, and to save money, Hanbury Brown selected two of the largest army-surplus anti-aircraft searchlights that he could find left over from the London Blitz. The lamps were removed and replaced with high-performance photomultipliers, and the units were installed on two train cars that could run along a railroad siding that crossed the Jodrell Bank grounds.

*Fig. Stellar Interferometers: (Left) Michelson Stellar Field Interferometer. (Right) Hanbury Brown Twiss Stellar Intensity Interferometer.*

The target of the first test of the intensity interferometer was Sirius, the Dog Star. Sirius was chosen because it is the brightest star in the night sky and was close to Earth at 8.6 light years and hence would be expected to have a relatively large angular size. The observations began at the start of winter in 1955, but the legendary English weather proved an obstacle. In addition to endless weeks of cloud cover, on many nights dew formed on the reflecting mirrors, making it necessary to install heaters. It took more than three months to make 60 operational attempts to accumulate a mere 18 hours of observations [13]. But it worked! The angular size of Sirius was measured for the first time. It subtended an angle of approximately 6 milliarcseconds (mas), which was well within the expected range for such a main sequence blue star. This angle is equivalent to observing a house on the Moon from the Earth. No single non-interferometric telescope on Earth, or in Earth orbit, has that kind of resolution, even today. Once again, Sirus was the testbed of a new observational technology. Hanbury Brown and Twiss went on the measure the diameters of dozens of stars.

Adaptive Optics

Any undergraduate optics student can tell you that bigger telescopes have higher spatial resolution. But this is only true up to a point. When telescope diameters become not much bigger than about 10 inches, the images they form start to dance, caused by thermal fluctuations in the atmosphere. Large telescopes can still get “lucky” at moments when the atmosphere is quiet, but this usually only happens for a fraction of a second before the fluctuation set in again. This is the primary reason that the Hubble Space Telescope was placed in Earth orbit above the atmosphere, and why the James Webb Space Telescope is flying a million miles away from the Earth. But that is not the end of Earth-based large telescoped. The Very Large Telescope (VLT) has a primary diameter of 8 meters, and the Extremely Large Telescope (ELT), coming online soon, has an even bigger diameter of 40 meters. How do these work under the atmospheric blanket? The answer is adaptive optics.

Adaptive optics uses active feedback to measure the dancing images caused by the atmosphere and uses the information to control a flexible array of mirror elements to exactly cancel out the effects of the atmospheric fluctuations. In the early days of adaptive-optics development, the applications were more military than astronomic, but advances made in imaging enemy satellites soon was released to the astronomers. The first civilian demonstrations of adaptive optics were performed in 1977 when researchers at Bell Labs [14] and at the Space Sciences Lab at UC Berkeley [15] each made astronomical demonstrations of improved seeing of the star Sirius using adaptive optics. The field developed rapidly after that, but once again Sirius had led the way.

Star Travel

The day is fast approaching when humans will begin thinking seriously of visiting nearby stars—not in person at first, but with unmanned spacecraft that can telemeter information back to Earth. Although Sirius is not the closest star to Earth—it is 8.6 lightyears away while Alpha Centauri is almost twice as close at only 4.2 lightyears away—it may be the best target for an unmanned spacecraft. The reason is its brightness.

Stardrive technology is still in its infancy—most of it is still on drawing boards. Therefore, the only “mature” technology we have today is light pressure on solar sails. Within the next 50 years or so we will have the technical ability to launch a solar sail towards a nearby star and accelerate it to a good fraction of the speed of light. The problem is decelerating the spaceship when it arrives at its destination, otherwise it will go zipping by with only a few seconds to make measurements after its long trek there.

*Fig. NASA’s solar sail demonstrator unit (artist’s rendering).*

A better idea is to let the star light push against the solar sail to decelerate it to orbital speed by the time it arrives. That way, the spaceship can orbit the target star for years. This is a possibility with Sirius. Because it is so bright, its light can decelerate the spaceship even when it is originally moving at relativistic speeds. By one calculation, the trip to Sirius, including the deceleration and orbital insertion, should only take about 69 years [16]. That’s just one lifetime. Signals could be beaming back from Sirius by as early as 2100—within the lifetimes of today’s children.

Footnotes

[1] The section is excerpted from D. D. Nolte, The Fall and Rise of the Doppler Effect, Physics Today (2020)

[2] W. Huggins, “Further observations on the spectra of some of the stars and nebulae, with an attempt to determine therefrom whether these bodies are moving towards or from the earth, also observations on the spectra of the sun and of comet II,” Philos. Trans. R. Soc. London vol. 158, pp. 529-564, 1868. The correct value is -5.5 km/sec approaching Earth. Huggins got the magnitude and even the sign wrong.

[3] in Hearnshaw, The Analysis of Starlight (Cambridge University Press, 2014), pg. 89

[4] The Potsdam Observatory was where the American Albert Michelson built his first interferometer while studying with Helmholtz in Berlin.

[5] Vogel, H. C. Publik. der astrophysik. Observ. Potsdam 1: 1. (1892)

[6] A. Belopolsky, “On an apparatus for the laboratory demonstration of the Doppler-Fizeau principle,” Astrophysical Journal, vol. 13, pp. 15-24, Jan 1901.

[7] https://adsabs.harvard.edu/full/1980QJRAS..21..246H

[8] D. D. Nolte, Interference: The History of Optical Interferometry and the Scientists who Tamed Light (Oxford University Press, 2023)

[9] M. Ryle and D. D. Vonberg, “Solar Radiation on 175 Mc/sec,” Nature, vol. 158 (1946): pp. 339-340.; K. I. Kellermann and J. M. Moran, “The development of high-resolution imaging in radio astronomy,” Annual Review of Astronomy and Astrophysics, vol. 39, (2001): pp. 457-509.

[10] M. Ryle, ” Solar radio emissions and sunspots,” Nature, vol. 161, no. 4082 (1948): pp. 136-136.

[11] R. H. Brown, The intensity interferometer; its application to astronomy (London, New York, Taylor & Francis; Halsted Press, 1974).

[12] R. H. Brown, Boffin : A personal story of the early days of radar and radio astronomy (Adam Hilger, 1991), p. 106.

[13] R. H. Brown and R. Q. Twiss. ” Test of a new type of stellar interferometer on Sirius.” Nature 178, no. 4541 (1956): pp. 1046-1048.

[14] S. L. McCall, T. R. Brown, and A. Passner, “IMPROVED OPTICAL STELLAR IMAGE USING A REAL-TIME PHASE-CORRECTION SYSTEM – INITIAL RESULTS,” Astrophysical Journal, vol. 211, no. 2, pp. 463-468, (1977)

[15] A. Buffington, F. S. Crawford, R. A. Muller, and C. D. Orth, “1ST OBSERVATORY RESULTS WITH AN IMAGE-SHARPENING TELESCOPE,” Journal of the Optical Society of America, vol. 67, no. 3, pp. 304-305, 1977 (1977)

[16] https://www.newscientist.com/article/2128443-quickest-we-could-visit-another-star-is-69-years-heres-how/

August 17, 2023November 27, 2023 by David D. Nolte

New Book: Interference. The Scientists who Tamed Light

Interference: The History of Optical Interferometry and the Scientists who Tamed Light, is published! It is available now at Oxford University Press and can be pre-ordered at Amazon and Barnes&Nobles to ship on Sept. 6.

The synopses of the first chapters can be found in my previous blog. Here are previews of the final chapters.

Chapter 6. Across the Universe: Exoplanets, Black Holes and Gravitational Waves

Across the Universe: Gravitational Waves, Black Holes and the Search for Exoplanets describes the latest discoveries of interferometry in astronomy including the use of nulling interferometry in the Very Large Telescope Interferometer (VLTI) to detect exoplanets orbiting distant stars. The much larger Event Horizon Telescope (EHT) used long baseline interferometry and closure phase advanced by Roger Jenison to make the first image of a black hole. The Laser Interferometric Gravitational Observatory (LIGO) represented a several-decade-long drive to detect the first gravitational waves first predicted by Albert Einstein a hundred years ago.

Chapter 7. Two Faces of Microscopy: Diffraction and Interference

From the astronomically large dimensions of outer space to the microscopically small dimensions of inner space, optical interference pushes the resolution limits of imaging.

Two Faces of Microscopy: Diffraction and Interference describes the development of microscopic principles starting with Joseph Fraunhofer and the principle of diffraction gratings that was later perfected by Henry Rowland for high-resolution spectroscopy. The company of Carl Zeiss advanced microscope technology after enlisting the help of Ernst Abbe who formed a new theory of image formation based on light interference. These ideas were extended by Fritz Zernike in the development of phase-contrast microscopy. The ultimate resolution of microscopes, defined by Abbe and known as the Abbe resolution limit, turned out not to be a fundamental limit, but was surpassed by super-resolution microscopy using concepts of interference microscopy and structured illumination.

Chapter 8. Holographic Dreams of Princess Leia: Crossing Beams

The coherence of laser light is like a brilliant jewel that sparkles in the darkness, illuminating life, probing science and projecting holograms in virtual worlds.

Holographic Dreams of Princess Leia: Crossing Beams presents the history of holography, beginning with the original ideas of Denis Gabor who invented optical holography as a means to improve the resolution of electron microscopes. Holography became mainstream after the demonstrations by Emmett Leith and Juris Upatnieks using lasers that were first demonstrated by Ted Maiman at Hughes Research Lab after suggestions by Charles Townes on the operating principles of the optical maser. Dynamic holography takes place in crystals that exhibit the photorefractive effect that are useful for adaptive interferometry. Holographic display technology is under development, using ideas of holography merged with light-field displays that were first developed by Gabriel Lippmann.

Chapter 9. Photon Interference: The Foundations of Quantum Communication and Computing

What is the image of one photon interfering? Better yet, what is the image of two photons interfering? The answer to this crucial question laid the foundation for quantum communication.

Photon Interference: The Foundations of Quantum Communication moves the story of interferometry into the quantum realm, beginning with the Einstein-Podolski-Rosen paradox and the principle of quantum entanglement that was refined by David Bohm who tried to banish uncertainty from quantum theory. John Bell and John Clauser pushed the limits of what can be known from quantum measurement as Clauser tested Bell’s inequalities, confirming the fundamental nonlocal character of quantum systems. Leonard Mandel pushed quantum interference into the single-photon regime, discovering two-photon interference fringes that illustrated deep concepts of quantum coherence. Quantum communication began with quantum cryptography and developed into quantum teleportation that can provide the data bus of future quantum computers.

Chapter 10. The Quantum Advantage: Interferometric Computing

The Quantum Advantage: Interferometric Computing describes the development of quantum algorithms and quantum computing beginning with the first quantum algorithm invented by David Deutsch as a side effect of his attempt to prove the multiple world interpretation of quantum theory. Peter Shor found a quantum algorithm that could factor the product of primes and that threatened all secure communications in the world. Once the usefulness of quantum algorithms was recognized, quantum computing hardware ideas developed rapidly into quantum circuits supported by quantum logic gates. The limitation of optical interactions, that hampered the development of controlled quantum gates, led to the proposal of linear optical quantum computing and boson sampling in a complex cascade of single-photon interferometers that has been used to demonstrate quantum supremacy, also known as quantum computational advantage, using photonic integrated circuits.

New from Oxford Press: Interference

A popular account of the trials and toils of the scientists and engineers who tamed light and used it to probe the universe.

Available at Amazon

and at Oxford University Press

and at Barnes & Noble

July 26, 2023November 27, 2023 by David D. Nolte

Book Preview: Interference. The History of Optical Interferometry

This history of interferometry has many surprising back stories surrounding the scientists who discovered and explored one of the most important aspects of the physics of light—interference. From Thomas Young who first proposed the law of interference, and Augustin Fresnel and Francois Arago who explored its properties, to Albert Michelson, who went almost mad grappling with literal firestorms surrounding his work, these scientists overcame personal and professional obstacles on their quest to uncover light’s secrets. The book’s stories, told around the topic of optics, tells us something more general about human endeavor as scientists pursue science.

Interference: The History of Optical Interferometry and the Scientists who Tamed Light, was published Ag. 6 and is available at Oxford University Press and Amazon. Here is a brief preview of the frist several chapters:

Chapter 1. Thomas Young Polymath: The Law of Interference

The chapter, Thomas Young Polymath: The Law of Interference, begins with the story of the invasion of Egypt in 1798 by Napoleon Bonaparte as the unlikely link among a set of epic discoveries that launched the modern science of light. The story of interferometry passes from the Egyptian campaign and the discovery of the Rosetta Stone to Thomas Young. Young was a polymath, known for his facility with languages that helped him decipher Egyptian hieroglyphics aided by the Rosetta Stone. He was also a city doctor who advised the admiralty on the construction of ships, and he became England’s premier physicist at the beginning of the nineteenth century, building on the wave theory of Huygens, as he challenged Newton’s particles of light. But his theory of the wave nature of light was controversial, attracting sharp criticism that would pass on the task of refuting Newton to a new generation of French optical physicists.

Chapter 2. The Fresnel Connection: Particles versus Waves

Augustin Fresnel was an intuitive genius whose talents were almost squandered on his job building roads and bridges in the backwaters of France until he was discovered and rescued by Francois Arago.

The Fresnel Connection: Particles versus Waves describes the campaign of Arago and Fresnel to prove the wave nature of light based on Fresnel’s theory of interfering waves in diffraction. Although the discovery of the polarization of light by Etienne Malus posed a stark challenge to the undulationists, the application of wave interference, with the superposition principle of Daniel Bernoulli, provided the theoretical framework for the ultimate success of the wave theory. The final proof came through the dramatic demonstration of the Spot of Arago.

Chapter 3. At Light Speed: The Birth of Interferometry

At Light Speed: The Birth of Interferometry tells how Arago attempted to use Snell’s Law to measure the effect of the Earth’s motion through space but found no effect, in contradiction to predictions using Newton’s particle theory of light. Direct measurements of the speed of light were made by Hippolyte Fizeau and Leon Foucault who originally began as collaborators but had an epic falling-out that turned into an intense competition. Fizeau won priority for the first measurement, but Foucault surpassed him by using the Arago interferometer to measure the speed of light in air and water with increasing accuracy. Jules Jamin later invented one of the first interferometric instruments for use as a refractometer.

Chapter 4. After the Gold Rush: The Trials of Albert Michelson

After the Gold Rush: The Trials of Albert Michelson tells the story of Michelson’s youth growing up in the gold fields of California before he was granted an extraordinary appointment to Annapolis by President Grant. Michelson invented his interferometer while visiting Hermann von Helmholtz in Berlin, Germany, as he sought to detect the motion of the Earth through the luminiferous ether, but no motion was detected. After returning to the States and a faculty position at Case University, he met Edward Morley, and the two continued the search for the Earth’s motion, concluding definitively its absence. The Michelson interferometer launched a menagerie of interferometers (including the Fabry-Perot interferometer) that ushered in the golden age of interferometry.

Chapter 5. Stellar Interference: Measuring the Stars

Stellar Interference: Measuring the Stars brings the story of interferometry to the stars as Michelson proposed stellar interferometry, first demonstrated on the Galilean moons of Jupiter, followed by an application developed by Karl Schwarzschild for binary stars, and completed by Michelson with observations encouraged by George Hale on the star Betelgeuse. However, the Michelson stellar interferometry had stability limitations that were overcome by Hanbury Brown and Richard Twiss who developed intensity interferometry based on the effect of photon bunching. The ultimate resolution of telescopes was achieved after the development of adaptive optics that used interferometry to compensate for atmospheric turbulence.

And More

The last 5 chapters bring the story from Michelson’s first stellar interferometer into the present as interferometry is used today to search for exoplanets, to image distant black holes half-way across the universe and to detect gravitational waves using the most sensitive scientific measurement apparatus ever devised.

Chapter 6. Across the Universe: Exoplanets, Black Holes and Gravitational Waves

Moving beyond the measurement of star sizes, interferometry lies at the heart of some of the most dramatic recent advances in astronomy, including the detection of gravitational waves by LIGO, the imaging of distant black holes and the detection of nearby exoplanets that may one day be visited by unmanned probes sent from Earth.

Chapter 7. Two Faces of Microscopy: Diffraction and Interference

The complement of the telescope is the microscope. Interference microscopy allows invisible things to become visible and for fundamental limits on image resolution to be blown past with super-resolution at the nanoscale, revealing the intricate workings of biological systems with unprecedented detail.

Chapter 8. Holographic Dreams of Princess Leia: Crossing Beams

Holography is the direct legacy of Young’s double slit experiment, as coherent sources of light interfere to record, and then reconstruct, the direct scattered fields from illuminated objects. Holographic display technology promises to revolutionize virtual reality.

Chapter 9. Photon Interference: The Foundations of Quantum Communication and Computing

Quantum information science, at the forefront of physics and technology today, owes much of its power to the principle of interference among single photons.

Chapter 10. The Quantum Advantage: Interferometric Computing

Photonic quantum systems have the potential to usher in a new information age using interference in photonic integrated circuits.

A popular account of the trials and toils of the scientists and engineers who tamed light and used it to probe the universe.

Available at Amazon

and at Oxford University Press

and at Barnes & Noble

May 29, 2023October 18, 2023 by David D. Nolte

Io, Europa, Ganymede, and Callisto: Galileo’s Moons in the History of Science

At Light Speed, History of Dynamics
Albert Michelson, Callisto, Cassini, Europa, Galileo, Ganymede, History of Science, Interferometry, Io, Jupiter, Rømer, Speed of Light
2 Comments

When Galileo trained his crude telescope on the planet Jupiter, hanging above the horizon in 1610, and observed moons orbiting a planet other than Earth, it created a quake whose waves have rippled down through the centuries to today. Never had such hard evidence been found that supported the Copernican idea of non-Earth-centric orbits, freeing astronomy and cosmology from a thousand years of error that shaded how people thought.

The Earth, after all, was not the center of the Universe.

Galileo’s moons: the Galilean Moons—Io, Europa, Ganymede, and Callisto—have drawn our eyes skyward now for over 400 years. They have been the crucible for numerous scientific discoveries, serving as a test bed for new ideas and new techniques, from the problem of longitude to the speed of light, from the birth of astronomical interferometry to the beginnings of exobiology. Here is a short history of Galileo’s Moons in the history of physics.

Galileo (1610): Celestial Orbits

In late 1609, Galileo (1564 – 1642) received an unwelcome guest to his home in Padua—his mother. She was not happy with his mistress, and she was not happy with his chosen profession, but she was happy to tell him so. By the time she left in early January 1610, he was yearning for something to take his mind off his aggravations, and he happened to point his new 20x telescope in the direction of the planet Jupiter hanging above the horizon [1]. Jupiter appeared as a bright circular spot, but nearby were three little stars all in line with the planet. The alignment caught his attention, and when he looked again the next night, the position of the stars had shifted. On successive nights he saw them shift again, sometimes disappearing into Jupiter’s bright disk. Several days later he realized that there was a fourth little star that was also behaving the same way. At first confused, he had a flash of insight—the little stars were orbiting the planet. He quickly understood that just as the Moon orbited the Earth, these new “Medicean Planets” were orbiting Jupiter. In March 1610, Galileo published his findings in Siderius Nuncius (The Starry Messenger).

Page from Galileo’s Starry Messenger showing the positions of the moon of Jupiter

It is rare in the history of science for there not to be a dispute over priority of discovery. Therefore, by an odd chance of fate, on the same nights that Galileo was observing the moons of Jupiter with his telescope from Padua, the German astronomer Simon Marius (1573 – 1625) also was observing them through a telescope of his own from Bavaria. It took Marius four years to publish his observations, long after Galileo’s Siderius had become a “best seller”, but Marius took the opportunity to claim priority. When Galileo first learned of this, he called Marius “a poisonous reptile” and “an enemy of all mankind.” But harsh words don’t settle disputes, and the conflicting claims of both astronomers stood until the early 1900’s when a scientific enquiry looked at the hard evidence. By that same odd chance of fate that had compelled both men to look in the same direction around the same time, the first notes by Marius in his notebooks were dated to a single day after the first notes by Galileo! Galileo’s priority survived, but Marius may have had the last laugh. The eternal names of the “Galilean” moons—Io, Europe, Ganymede and Callisto—were given to them by Marius.

Picard and Cassini (1671): Longitude

The 1600’s were the Age of Commerce for the European nations who relied almost exclusively on ships and navigation. While latitude (North-South) was easily determined by measuring the highest angle of the sun above the southern horizon, longitude (East-West) relied on clocks which were notoriously inaccurate, especially at sea.

The Problem of Determining Longitude at Sea is the subject of Dava Sobel’s thrilling book Longitude (Walker, 1995) [2] where she reintroduced the world to what was once the greatest scientific problem of the day. Because almost all commerce was by ships, the determination of longitude at sea was sometimes the difference between arriving safely in port with a cargo or being shipwrecked. Galileo knew this, and later in his life he made a proposal to the King of Spain to fund a scheme to use the timings of the eclipses of his moons around Jupiter to serve as a “celestial clock” for ships at sea. Galileo’s grant proposal went unfunded, but the possibility of using the timings of Jupiter’s moons for geodesy remained an open possibility, one which the King of France took advantage of fifty years later.

In 1671 the newly founded Academie des Sciences in Paris funded an expedition to the site of Tycho Brahe’s Uranibourg Observatory in Hven, Denmark, to measure the time of the eclipses of the Galilean moons observed there to be compared the time of the eclipses observed in Paris by Giovanni Cassini (1625 – 1712). When the leader of the expedition, Jean Picard (1620 – 1682), arrived in Denmark, he engaged the services of a local astronomer, Ole Rømer (1644 – 1710) to help with the observations of over 100 eclipses of the Galilean moon Io by the planet Jupiter. After the expedition returned to France, Cassini and Rømer calculated the time differences between the observations in Paris and Hven and concluded that Galileo had been correct. Unfortunately, observing eclipses of the tiny moon from the deck of a ship turned out not to be practical, so this was not the long-sought solution to the problem of longitude, but it contributed to the early science of astrometry (the metrical cousin of astronomy). It also had an unexpected side effect that forever changed the science of light.

Ole Rømer (1676): The Speed of Light

Although the differences calculated by Cassini and Rømer between the times of the eclipses of the moon Io between Paris and Hven were small, on top of these differences was superposed a surprisingly large effect that was shared by both observations. This was a systematic shift in the time of eclipse that grew to a maximum value of 22 minutes half a year after the closest approach of the Earth to Jupiter and then decreased back to the original time after a full year had passed and the Earth and Jupiter were again at their closest approach. At first Cassini thought the effect might be caused by a finite speed to light, but he backed away from this conclusion because Galileo had shown that the speed of light was unmeasurably fast, and Cassini did not want to gainsay the old master.

Rømer, on the other hand, was less in awe of Galileo’s shadow, and he persisted in his calculations and concluded that the 22 minute shift was caused by the longer distance light had to travel when the Earth was farthest away from Jupiter relative to when it was closest. He presented his results before the Academie in December 1676 where he announced that the speed of light, though very large, was in fact finite. Unfortnately, Rømer did not have the dimensions of the solar system at his disposal to calculate an actual value for the speed of light, but the Dutch mathematician Huygens did.

When Huygens read the proceedings of the Academie in which Rømer had presented his findings, he took what he knew of the radius of Earth’s orbit and the distance to Jupiter and made the first calculation of the speed of light. He found a value of 220,000 km/second (kilometers did not exist yet, but this is the equivalent of what he calculated). This value is 26 percent smaller than the true value, but it was the first time a number was given to the finite speed of light—based fundamentally on the Galilean moons. For a popular account of the story of Picard and Rømer and Huygens and the speed of light, see Ref. [3].

Michelson (1891): Astronomical Interferometry

Albert Michelson (1852 – 1931) was the first American to win the Nobel Prize in Physics. He received the award in 1907 for his work to replace the standard meter, based on a bar of metal housed in Paris, with the much more fundamental wavelength of red light emitted by Cadmium atoms. His work in Paris came on the heels of a new and surprising demonstration of the use of interferometry to measure the size of astronomical objects.

The wavelength of light (a millionth of a meter) seems ill-matched to measuring the size of astronomical objects (thousands of meters) that are so far from Earth (billions of meters). But this is where optical interferometry becomes so important. Michelson realized that light from a distant object, like a Galilean moon of Jupiter, would retain some partial coherence that could be measured using optical interferometry. Furthermore, by measuring how the interference depended on the separation of slits placed on the front of a telescope, it would be possible to determine the size of the astronomical object.

From left to right: Walter Adams, Albert Michelson, Walther Mayer, Albert Einstein, Max Ferrand, and Robert Milliken. Photo taken at Caltech.

In 1891, Michelson traveled to California where the Lick Observatory was poised high above the fog and dust of agricultural San Jose (a hundred years before San Jose became the capitol of high-tech Silicon Valley). Working with the observatory staff, he was able to make several key observations of the Galilean moons of Jupiter. These were just close enough that their sizes could be estimated (just barely) from conventional telescopes. Michelson found from his calculations of the interference effects that the sizes of the moons matched the conventional sizes to within reasonable error. This was the first demonstration of astronomical interferometry which has burgeoned into a huge sub-discipline of astronomy today—based originally on the Galilean moons [4].

Pioneer (1973 – 1974): The First Tour

Pioneer 10 was launched on March 3, 1972 and made its closest approach to Jupiter on Dec. 3, 1973. Pioneer 11 was launched on April 5, 1973 and made its closest approach to Jupiter on Dec. 3, 1974 and later was the first spacecraft to fly by Saturn. The Pioneer spacecrafts were the first to leave the solar system (there have now been 5 that have left, or will leave, the solar system). The cameras on the Pioneers were single-pixel instruments that made line-scans as the spacecraft rotated. The point light detector was a Bendix Channeltron photomultiplier detector, which was a vacuum tube device (yes vacuum tube!) operating at a single-photon detection efficiency of around 10%. At the time of the system design, this was a state-of-the-art photon detector. The line scanning was sufficient to produce dramatic photographs (after extensive processing) of the giant planets. The much smaller moons were seen with low resolution, but were still the first close-ups ever to be made of Galileo’s moons.

Voyager (1979): The Grand Tour

Voyager 1 was launched on Sept. 5, 1977 and Voyager 2 was launched on August 20, 1977. Although Voyager 1 was launched second, it was the first to reach Jupiter with closest approach on March 5, 1979. Voyager 2 made its closest approach to Jupiter on July 9, 1979.

In the Fall of 1979, I had the good fortune to be an undergraduate at Cornell University when Carl Sagan gave an evening public lecture on the Voyager fly-bys, revealing for the first time the amazing photographs of not only Jupiter but of the Galilean Moons. Sitting in the audience listening to Sagan, a grand master of scientific story telling, made you feel like you were a part of history. I have never been so convinced of the beauty and power of science and technology as I was sitting in the audience that evening.

The camera technology on the Voyagers was a giant leap forward compared to the Pioneer spacecraft. The Voyagers used cathode ray vidicon cameras, like those used in television cameras of the day, with high-resolution imaging capabilities. The images were spectacular, displaying alien worlds in high-def for the first time in human history: volcanos and lava flows on the moon of Io; planet-long cracks in the ice-covered surface of Europa; Callisto’s pock-marked surface; Ganymede’s eerie colors.

The Voyager’s discoveries concerning the Galilean Moons were literally out of this world. Io was discovered to be a molten planet, its interior liquified by tidal-force heating from its nearness to Jupiter, spewing out sulfur lava onto a yellowed terrain pockmarked by hundreds of volcanoes, sporting mountains higher than Mt. Everest. Europa, by contrast, was discovered to have a vast flat surface of frozen ice, containing no craters nor mountains, yet fractured by planet-scale ruptures stained tan (for unknown reasons) against the white ice. Ganymede, the largest moon in the solar system, is a small planet, larger than Mercury. The Voyagers revealed that it had a blotchy surface with dark cratered patches interspersed with light smoother patches. Callisto, again by contrast, was found to be the most heavily cratered moon in the solar system, with its surface pocked by countless craters.

Galileo (1995): First in Orbit

The first mission to orbit Jupiter was the Galileo spacecraft that was launched, not from the Earth, but from Earth orbit after being delivered there by the Space Shuttle Atlantis on Oct. 18, 1989. Galileo arrived at Jupiter on Dec. 7, 1995 and was inserted into a highly elliptical orbit that became successively less eccentric on each pass. It orbited Jupiter for 8 years before it was purposely crashed into the planet (to prevent it from accidentally contaminating Europa that may support some form of life).

Galileo made many close passes to the Galilean Moons, providing exquisite images of the moon surfaces while its other instruments made scientific measurements of mass and composition. This was the first true extended study of Galileo’s Moons, establishing the likely internal structures, including the liquid water ocean lying below the frozen surface of Europa. As the largest body of liquid water outside the Earth, it has been suggested that some form of life could have evolved there (or possibly been seeded by meteor ejecta from Earth).

Juno (2016): Still Flying

The Juno spacecraft was launched from Cape Canaveral on Aug. 5, 2011 and entered a Jupiter polar orbit on July 5, 2016. The mission has been producing high-resolution studies of the planet. The mission was extended in 2021 to last to 2025 to include several close fly-bys of the Galilean Moons, especially Europa, which will be the object of several upcoming missions because of the possibility for the planet to support evolved life. These future missions include NASA’s Europa Clipper Mission, the ESA’s Jupiter Icy Moons Explorer, and the Io Volcano Observer.

Epilog (2060): Colonization of Callisto

In 2003, NASA identified the moon Callisto as the proposed site of a manned base for the exploration of the outer solar system. It would be the next most distant human base to be established after Mars, with a possible start date by the mid-point of this century. Callisto was chosen because it is has a low radiation level (being the farthest from Jupiter of the large moons) and is geologically stable. It also has a composition that could be mined to manufacture rocket fuel. The base would be a short-term way-station (crews would stay for no longer than a month) for refueling before launching and using a gravity assist from Jupiter to sling-shot spaceships to the outer planets.

By David D. Nolte, May 29, 2023

[1] See Chapter 2, A New Scientist: Introducing Galileo, in David D. Nolte, Galileo Unbound (Oxford University Press, 2018).

[2] Dava Sobel, Longitude: The True Story of a Lone Genius who Solved the Greatest Scientific Problem of his Time (Walker, 1995)

[3] See Chap. 1, Thomas Young Polymath: The Law of Interference, in David D. Nolte, Interference: The History of Optical Interferometry and the Scientists who Tamed Light (Oxford University Press, 2023)

[4] See Chapter 5, Stellar Interference: Measuring the Stars, in David D. Nolte, Interference: The History of Optical Interferometry and the Scientists who Tamed Light (Oxford University Press, 2023).

March 22, 2023November 27, 2023 by David D. Nolte

Francois Arago and the Birth of Optical Science

An excerpt from the upcoming book “Interference: The History of Optical Interferometry and the Scientists who Tamed Light” describes how a handful of 19^th-century scientists laid the groundwork for one of the key tools of modern optics. Published in Optics and Photonics News, March 2023.

François Arago rose to the highest levels of French science and politics. Along the way, he met Augustin Fresnel and, together, they changed the course of optical science.

Link to OPN Article

New from Oxford Press: The History of Light and Interference (2023)

A popular account of the trials and toils of the scientists and engineers who tamed light and used it to probe the universe.

Available at Amazon

and at Oxford University Press

and at Barnes & Noble

May 8, 2022November 30, 2023 by David D. Nolte

The Many Worlds of the Quantum Beam Splitter

In one interpretation of quantum physics, when you snap your fingers, the trajectory you are riding through reality fragments into a cascade of alternative universes—one for each possible quantum outcome among all the different quantum states composing the molecules of your fingers.

This is the Many-Worlds Interpretation (MWI) of quantum physics first proposed rigorously by Hugh Everett in his doctoral thesis in 1957 under the supervision of John Wheeler at Princeton University. Everett had been drawn to this interpretation when he found inconsistencies between quantum physics and gravitation—topics which were supposed to have been his actual thesis topic. But his side-trip into quantum philosophy turned out to be a one-way trip. The reception of his theory was so hostile, no less than from Copenhagen and Bohr himself, that Everett left physics and spent a career at the Pentagon.

Resurrecting MWI in the Name of Quantum Information

Fast forward by 20 years, after Wheeler had left Princeton for the University of Texas at Austin, and once again a young physicist was struggling to reconcile quantum physics with gravity. Once again the many worlds interpretation of quantum physics seemed the only sane way out of the dilemma, and once again a side-trip became a life-long obsession.

David Deutsch, visiting Wheeler in the early 1980’s, became convinced that the many worlds interpretation of quantum physics held the key to paradoxes in the theory of quantum information (For the full story of Wheeler, Everett and Deutsch, see Ref [1]). He was so convinced, that he began a quest to find a physical system that operated on more information than could be present in one universe at a time. If such a physical system existed, it would be because streams of information from more than one universe were coming together and combining in a way that allowed one of the universes to “borrow” the information from the other.

It took only a year or two before Deutsch found what he was looking for—a simple quantum algorithm that yielded twice as much information as would be possible if there were no parallel universes. This is the now-famous Deutsch algorithm—the first quantum algorithm [2]. At the heart of the Deutsch algorithm is a simple quantum interference. The algorithm did nothing useful—but it convinced Deutsch that two universes were interfering coherently in the measurement process, giving that extra bit of information that should not have been there otherwise. A few years later, the Deutsch-Josza algorithm [2] expanded the argument to interfere an exponentially larger amount of information streams from an exponentially larger number of universes to create a result that was exponentially larger than any classical computer could produce. This marked the beginning of the quest for the quantum computer that is running red-hot today.

Deutsch’s “proof” of the many-worlds interpretation of quantum mechanics is not a mathematical proof but is rather a philosophical proof. It holds no sway over how physicists do the math to make their predictions. The Copenhagen interpretation, with its “spooky” instantaneous wavefunction collapse, works just fine predicting the outcome of quantum algorithms and the exponential quantum advantage of quantum computing. Therefore, the story of David Deutsch and the MWI may seem like a chimera—except for one fact—it inspired him to generate the first quantum algorithm that launched what may be the next revolution in the information revolution of modern society. Inspiration is important in science, because it lets scientists create things that had been impossible before.

But if quantum interference is the heart of quantum computing, then there is one physical system that has the ultimate simplicity that may yet inspire future generations of physicists to invent future impossible things—the quantum beam splitter. Nothing in the study of quantum interference can be simpler than a sliver of dielectric material sending single photons one way or another. Yet the outcome of this simple system challenges the mind and reminds us of why Everett and Deutsch embraced the MWI in the first place.

The Classical Beam Splitter

The so-called “beam splitter” is actually a misnomer. Its name implies that it takes a light beam and splits it into two, as if there is only one input. But every “beam splitter” has two inputs, which is clear by looking at the classical 50/50 beam splitter. The actual action of the optical element is the combination of beams into superpositions in each of the outputs. It is only when one of the input fields is zero, a special case, that the optical element acts as a beam splitter. In general, it is a beam combiner.

Given two input fields, the output fields are superpositions of the inputs

The square-root of two factor ensures that energy is conserved, because optical fluence is the square of the fields. This relation is expressed more succinctly as a matrix input-output relation

The phase factors in these equations ensure that the matrix is unitary

reflecting energy conservation.

The Quantum Beam Splitter

A quantum beam splitter is just a classical beam splitter operating at the level of individual photons. Rather than describing single photons entering or leaving the beam splitter, it is more practical to describe the properties of the fields through single-photon quantum operators

where the unitary matrix is the same as the classical case, but with fields replaced by the famous “a” operators. The photon operators operate on single photon modes. For instance, the two one-photon input cases are

where the creation operators operate on the vacuum state in each of the input modes.

The fundamental combinational properties of the beam splitter are even more evident in the quantum case, because there is no such thing as a single input to a quantum beam splitter. Even if no photons are directed into one of the input ports, that port still receives a “vacuum” input, and this vacuum input contributes to the fluctuations observed in the outputs.

The input-output relations for the quantum beam splitter are

The beam splitter operating on a one-photon input converts the input-mode creation operator into a superposition of out-mode creation operators that generates

The resulting output is entangled: either the single photon exits one port, or it exits the other. In the many worlds interpretation, the photon exits from one port in one universe, and it exits from the other port in a different universe. On the other hand, in the Copenhagen interpretation, the two output ports of the beam splitter are perfectly anti-correlated.

Fig. 1 Quantum Operations of a Beam Splitter. A beam splitter creates a quantum superposition of the input modes. The a-symbols are quantum number operators that create and annihilate photons. A single-photon input produces an entangled output that is a quantum superposition of the photon coming out of one output or the other.

The Hong-Ou-Mandel (HOM) Interferometer

When more than one photon is incident on a beam splitter, the fascinating effects of quantum interference come into play, creating unexpected outputs for simple inputs. For instance, the simplest example is a two photon input where a single photon is present in each input port of the beam splitter. The input state is represented with single creation operators operating on each vacuum state of each input port

creating a single photon in each of the input ports. The beam splitter operates on this input state by converting the input-mode creation operators into out-put mode creation operators to give

The important step in this process is the middle line of the equations: There is perfect destructive interference between the two single-photon operations. Therefore, both photons always exit the beam splitter from the same port—never split. Furthermore, the output is an entangled two-photon state, once more splitting universes.

Fig. 2 The HOM interferometer. A two-photon input on a beam splitter generates an entangled superposition of the two photons exiting the beam splitter always together.

The two-photon interference experiment was performed in 1987 by Chung Ki Hong and Jeff Ou, students of Leonard Mandel at the Optics Institute at the University of Rochester [4], and this two-photon operation of the beam splitter is now called the HOM interferometer. The HOM interferometer has become a center-piece for optical and photonic implementations of quantum information processing and quantum computers.

N-Photons on a Beam Splitter

Of course, any number of photons can be input into a beam splitter. For example, take the N-photon input state

The beam splitter acting on this state produces

The quantity on the right hand side can be re-expressed using the binomial theorem

where the permutations are defined by the binomial coefficient

The output state is given by

which is a “super” entangled state composed of N multi-photon states, involving N different universes.

Coherent States on a Quantum Beam Splitter

Surprisingly, there is a multi-photon input state that generates a non-entangled output—as if the input states were simply classical fields. These are the so-called coherent states, introduced by Glauber and Sudarshan [5, 6]. Coherent states can be described as superpositions of multi-photon states, but when a beam splitter operates on these superpositions, the outputs are simply 50/50 mixtures of the states. For instance, if the input scoherent tates are denoted by α and β, then the output states after the beam splitter are

This output is factorized and hence is NOT entangled. This is one of the many reasons why coherent states in quantum optics are considered the “most classical” of quantum states. In this case, a quantum beam splitter operates on the inputs just as if they were classical fields.

By David D. Nolte, May 8, 2022

References

[1] David D. Nolte, Interference: The History of Optical Interferometry and the Scientists who Tamed Light, (Oxford, July 2023)

[2] D. Deutsch, “Quantum-theory, the church-turing principle and the universal quantum computer,” Proceedings of the Royal Society of London Series a-Mathematical Physical and Engineering Sciences, vol. 400, no. 1818, pp. 97-117, (1985)

[3] D. Deutsch and R. Jozsa, “Rapid solution of problems by quantum computation,” Proceedings of the Royal Society of London Series a-Mathematical Physical and Engineering Sciences, vol. 439, no. 1907, pp. 553-558, Dec (1992)

[4] C. K. Hong, Z. Y. Ou, and L. Mandel, “Measurement of subpicosecond time intervals between 2 photons by interference,” Physical Review Letters, vol. 59, no. 18, pp. 2044-2046, Nov (1987)

[5] Glauber, R. J. (1963). “Photon Correlations.” Physical Review Letters 10(3): 84.

[6] Sudarshan, E. C. G. (1963). “Equivalence of semiclassical and quantum mechanical descriptions of statistical light beams.” Physical Review Letters 10(7): 277-&.; Mehta, C. L. and E. C. Sudarshan (1965). “Relation between quantum and semiclassical description of optical coherence.” Physical Review 138(1B): B274.

March 23, 2022June 1, 2023 by David D. Nolte

The Physics of Starflight: Proxima Centauri b or Bust!

The ability to travel to the stars has been one of mankind’s deepest desires. Ever since we learned that we are just one world in a vast universe of limitless worlds, we have yearned to visit some of those others. Yet nature has thrown up an almost insurmountable barrier to that desire–the speed of light. Only by traveling at or near the speed of light may we venture to far-off worlds, and even then, decades or centuries will pass during the voyage. The vast distances of space keep all the worlds isolated–possibly for the better.

Yet the closest worlds are not so far away that they will always remain out of reach. The very limit of the speed of light provides ways of getting there within human lifetimes. The non-intuitive effects of special relativity come to our rescue, and we may yet travel to the closest exoplanet we know of.

Proxima Centauri b

The closest habitable Earth-like exoplanet is Proxima Centauri b, orbiting the red dwarf star Proxima Centauri that is about 4.2 lightyears away from Earth. The planet has a short orbital period of only about 11 Earth days, but the dimness of the red dwarf puts the planet in what may be a habitable zone where water is in liquid form. Its official discovery date was August 24, 2016 by the European Southern Observatory in the Atacama Desert of Chile using the Doppler method. The Alpha Centauri system is a three-star system, and even before the discovery of the planet, this nearest star system to Earth was the inspiration for the Hugo-Award winning sci-fi trilogy The Three Body Problem by Chinese author Liu Cixin, originally published in 2008.

It may seem like a coincidence that the closest Earth-like planet to Earth is in the closest star system to Earth, but it says something about how common such exoplanets may be in our galaxy.

Artist’s rendition of Proxima Centauri b. From WikiCommons.

Breakthrough Starshot

There are already plans to send centimeter-sized spacecraft to Alpha Centauri. One such project that has received a lot of press is Breakthrough Starshot, a project of the Breakthrough Initiatives. Breakthrough Starshot would send around 1000 centimeter-sized camera-carrying laser-fitted spacecraft with 5-meter-diameter solar sails propelled by a large array of high-power lasers. The reason there are so many of these tine spacecraft is because of the collisions that are expected to take place with interstellar dust during the voyage. It is possible that only a few dozen of the craft will finally make it to Alpha Centauri intact.

Relative locations of the stars of the Alpha Centauri system. From ScienceNews.

As these spacecraft fly by the Alpha Centauri system, possibly within one hundred million miles of Proxima Centauri b, their tiny HR digital cameras will take pictures of the planet’s surface with enough resolution to see surface features. The on-board lasers will then transmit the pictures back to Earth. The travel time to the planet is expected to be 20 or 30 years, plus the four years for the laser information to make it back to Earth. Therefore, it would take a quarter century after launch to find out if Proxima Centauri b is habitable or not. The biggest question is whether it has an atmosphere. The red dwarf it orbits sends out catastrophic electromagnetic bursts that could strip the planet of its atmosphere thus preventing any chance for life to evolve or even to be sustained there if introduced.

There are multiple projects under consideration for travel to the Alpha Centauri systems. Even NASA has a tentative mission plan called the 2069 Mission (100 year anniversary of the Moon landing). This would entail a single spacecraft with a much larger solar sail than the small starshot units. Some of the mission plans proposed star-drive technology, such as nuclear propulsion systems, rather than light sails. Some of these designs could sustain a 1-g acceleration throughout the entire mission. It is intriguing to do the math on what such a mission could look like, in terms of travel time. Could we get an unmanned probe to Alpha Centauri in a matter of years? Let’s find out.

Special Relativity of Acceleration

The most surprising aspect of deriving the properties of relativistic acceleration using special relativity is that it works at all. We were all taught as young physicists that special relativity deals with inertial frames in constant motion. So the idea of frames that are accelerating might first seem to be outside the scope of special relativity. But one of Einstein’s key insights, as he sought to extend special relativity towards a more general theory, was that one can define a series of instantaneously inertial co-moving frames relative to an accelerating body. In other words, at any instant in time, the accelerating frame has an inertial co-moving frame. Once this is defined, one can construct invariants, just as in usual special relativity. And these invariants unlock the full mathematical structure of accelerating objects within the scope of special relativity.

For instance, the four-velocity and the four-acceleration in a co-moving frame for an object accelerating at g are given by

The object is momentarily stationary in the co-moving frame, which is why the four-velocity has only the zeroth component, and the four-acceleration has simply g for its first component.

Armed with these four-vectors, one constructs the invariants

and

This last equation is solved for the specific co-moving frame as

But the invariant is more general, allowing the expression

which yields

From these, putting them all together, one obtains the general differential equations for the change in velocity as a set of coupled equations

The solution to these equations is

where the unprimed frame is the lab frame (or Earth frame), and the primed frame is the frame of the accelerating object, for instance a starship heading towards Alpha Centauri. These equations allow one to calculate distances, times and speeds as seen in the Earth frame as well as the distances, times and speeds as seen in the starship frame. If the starship is accelerating at some acceleration g’ other than g, then the results are obtained simply by replacing g by g’ in the equations.

Relativistic Flight

It turns out that the acceleration due to gravity on our home planet provides a very convenient (but purely coincidental) correspondence

With a similarly convenient expression

These considerably simplify the math for a starship accelerating at g.

Let’s now consider a starship accelerating by g for the first half of the flight to Alpha Centauri, turning around and decelerating at g for the second half of the flight, so that the starship comes to a stop at its destination. The equations for the times to the half-way point are

This means at the midpoint that 1.83 years have elapsed on the starship, and about 3 years have elapsed on Earth. The total time to get to Alpha Centauri (and come to a stop) is then simply

It is interesting to look at the speed at the midpoint. This is obtained by

which is solved to give

This amazing result shows that the starship is traveling at 95% of the speed of light at the midpoint when accelerating at the modest value of g for about 3 years. Of course, the engineering challenges for providing such an acceleration for such a long time are currently prohibitive … but who knows? There is a lot of time ahead of us for technology to advance to such a point in the next century or so.

Figure. Time lapsed inside the spacecraft and on Earth for the probe to reach Alpha Centauri as a function of the acceleration of the craft. At 10 g’s, the time elapsed on Earth is a little less than 5 years. However, the signal sent back will take an additional 4.37 years to arrive for a total time of about 9 years.

Matlab alphacentaur.m

% alphacentaur.m
clear
format compact

g0 = 1;
L = 4.37;

for loop = 1:100
    
    g = 0.1*loop*g0;
    
    taup = (1/g)*acosh(g*L/2 + 1);
    tearth = (1/g)*sinh(g*taup);
    
    tauspacecraft(loop) = 2*taup;
    tlab(loop) = 2*tearth;
    
    acc(loop) = g;
    
end

figure(1)
loglog(acc,tauspacecraft,acc,tlab,'LineWidth',2)
legend('Space Craft','Earth Frame','FontSize',18)
xlabel('Acceleration (g)','FontSize',18)
ylabel('Time (years)','FontSize',18)
dum = set(gcf,'Color','White');
H = gca;
H.LineWidth = 2;
H.FontSize = 18;

To Centauri and Beyond

Once we get unmanned probes to Alpha Centauri, it opens the door to star systems beyond. The next closest are Barnards star at 6 Ly away, Luhman 16 at 6.5 Ly, Wise at 7.4 Ly, and Wolf 359 at 7.9 Ly. Several of these are known to have orbiting exoplanets. Ross 128 at 11 Ly and Lyuten at 12.2 Ly have known earth-like planets. There are about 40 known earth-like planets within 40 lightyears from Earth, and likely there are more we haven’t found yet. It is almost inconceivable that none of these would have some kind of life. Finding life beyond our solar system would be a monumental milestone in the history of science. Perhaps that day will come within this century.

By David D. Nolte, March 23, 2022

1. Thomas Young Polymath: The Law of Interference

2. The Fresnel Connection: Particles versus Waves

3. At Light Speed

4. After the Gold Rush

5. Stellar Interference

6. Across the Universe

7. Two Faces of Microscopy

8. Holographic Dreams of Princess Leia

9. Photon Interference

10. The Quantum Advantage

References:

Further Reading: The History of Light and Interference (2023)

Augustin Fresnel: Ironic Rebel of Physics

Stellar Aberration and the Fresnel Drag Coefficient

Fizeau’s Moving Water Experiment

Einstein’s Insight

Further Reading

Jean Picard at Uranibourg

Samuel Molyneux and Murder in Kew

James Bradley and the Light Wind

Sirius Through the Ages

The Heavens Move

The Sound of Sirius

White Dwarf

Static Interference

Adaptive Optics

Star Travel

Footnotes

Chapter 6. Across the Universe: Exoplanets, Black Holes and Gravitational Waves

Chapter 7. Two Faces of Microscopy: Diffraction and Interference

Chapter 8. Holographic Dreams of Princess Leia: Crossing Beams

Chapter 9. Photon Interference: The Foundations of Quantum Communication and Computing

Chapter 10. The Quantum Advantage: Interferometric Computing

New from Oxford Press: Interference

Chapter 1. Thomas Young Polymath: The Law of Interference

Chapter 2. The Fresnel Connection: Particles versus Waves

Chapter 3. At Light Speed: The Birth of Interferometry

Chapter 4. After the Gold Rush: The Trials of Albert Michelson

Chapter 5. Stellar Interference: Measuring the Stars

And More

Galileo (1610): Celestial Orbits

Picard and Cassini (1671): Longitude

Ole Rømer (1676): The Speed of Light

Michelson (1891): Astronomical Interferometry

Pioneer (1973 – 1974): The First Tour

Voyager (1979): The Grand Tour

Galileo (1995): First in Orbit

Juno (2016): Still Flying

Epilog (2060): Colonization of Callisto

New from Oxford Press: The History of Light and Interference (2023)

Resurrecting MWI in the Name of Quantum Information

The Classical Beam Splitter

The Quantum Beam Splitter

The Hong-Ou-Mandel (HOM) Interferometer

N-Photons on a Beam Splitter

Coherent States on a Quantum Beam Splitter

Read more in “Interference” (New from Oxford University Press, 2023)

References

Proxima Centauri b

Breakthrough Starshot

Special Relativity of Acceleration

Relativistic Flight

Matlab alphacentaur.m

To Centauri and Beyond

Further Reading