Christian Andreas Doppler (1803 – 1853) was born in Salzburg, Austria, to a longstanding family of stonemasons.  As a second son, he was expected to help his older brother run the business, so his Father had him tested in his 18^th year for his suitability for a career in business.  The examiner Simon Stampfer (1790 – 1864), an Austrian mathematician and inventor teaching at the Lyceum in Salzburg, discovered that Doppler had a gift for mathematics and was better suited for a scientific career.  Stampfer’s enthusiasm convinced Doppler’s father to enroll him in the Polytechnik Institute in Vienna (founded only a few years earlier in 1815) where he took classes in mathematics, mechanics and physics [1] from 1822 to 1825.  Doppler excelled in his courses, but was dissatisfied with the narrowness of the education, yearning for more breadth and depth in his studies and for more significance in his positions, feelings he would struggle with for his entire short life.  He left Vienna, returning to the Lyceum in Salzburg to round out his education with philosophy, languages and poetry.  Unfortunately, this four-year detour away from technical studies impeded his ability to gain a permanent technical position, so he began a temporary assistantship with a mathematics professor at Vienna.  As he approached his 30^th birthday this term expired without prospects.  He was about to emigrate to America when he finally received an offer to teach at a secondary school in Prague.

To read about the attack by Joseph Petzval on Doppler’s effect and the effect it had on Doppler, see my feature article “The Fall and Rise of the Doppler Effect“ in Physics Today, 73(3) 30, March (2020).

Salzburg Austria

Doppler in Prague

Prague gave Doppler new life.  He was a professor with a position that allowed him to marry the daughter of a sliver and goldsmith from Salzburg.  He began to publish scholarly papers, and in 1837 was appointed supplementary professor of Higher Mathematics and Geometry at the Prague Technical Institute, promoted to full professor in 1841.  It was here that he met the unusual genius Bernard Bolzano (1781 – 1848), recently returned from political exile in the countryside.  Bolzano was a philosopher and mathematician who developed rigorous concepts of mathematical limits and is famous today for his part in the Bolzano-Weierstrass theorem in functional analysis, but he had been too liberal and too outspoken for the conservative Austrian regime and had been dismissed from the University in Prague in 1819.  He was forbidden to publish his work in Austrian journals, which is one reason why much of Bolzano’s groundbreaking work in functional analysis remained unknown during his lifetime.  However, he participated in the Bohemian Society for Science from a distance, recognizing the inventive tendencies in the newcomer Doppler and supporting him for membership in the Bohemian Society.  When Bolzano was allowed to return in 1842 to the Polytechnic Institute in Prague, he and Doppler became close friends as kindred spirits. 

Prague, Czech Republic

On May 25, 1842, Bolzano presided as chairman over a meeting of the Bohemian Society for Science on the day that Doppler read a landmark paper on the color of stars to a meagre assembly of only five regular members of the Society [2].  The turn-out was so small that the meeting may have been held in the robing room of the Society rather than in the meeting hall itself.  Leading up to this famous moment, Doppler’s interests were peripatetic, ranging widely over mathematical and physical topics, but he had lately become fascinated by astronomy and by the phenomenon of stellar aberration.  Stellar aberration was discovered by James Bradley in 1729 and explained as the result of the Earth’s yearly motion around the Sun, causing the apparent location of a distant star to change slightly depending on the direction of the Earth’s motion.  Bradley explained this in terms of the finite speed of light and was able to estimate it to within several percent [3].  As Doppler studied Bradley aberration, he wondered how the relative motion of the Earth would affect the color of the star.  By making a simple analogy of a ship traveling with, or against, a series of ocean waves, he concluded that the frequency of impact of the peaks and troughs of waves on the ship was no different than the arrival of peaks and troughs of the light waves impinging on the eye.  Because perceived color was related to the frequency of excitation in the eye, he concluded that the color of light would be slightly shifted to the blue if approaching, and to the red if receding from, the light source. 

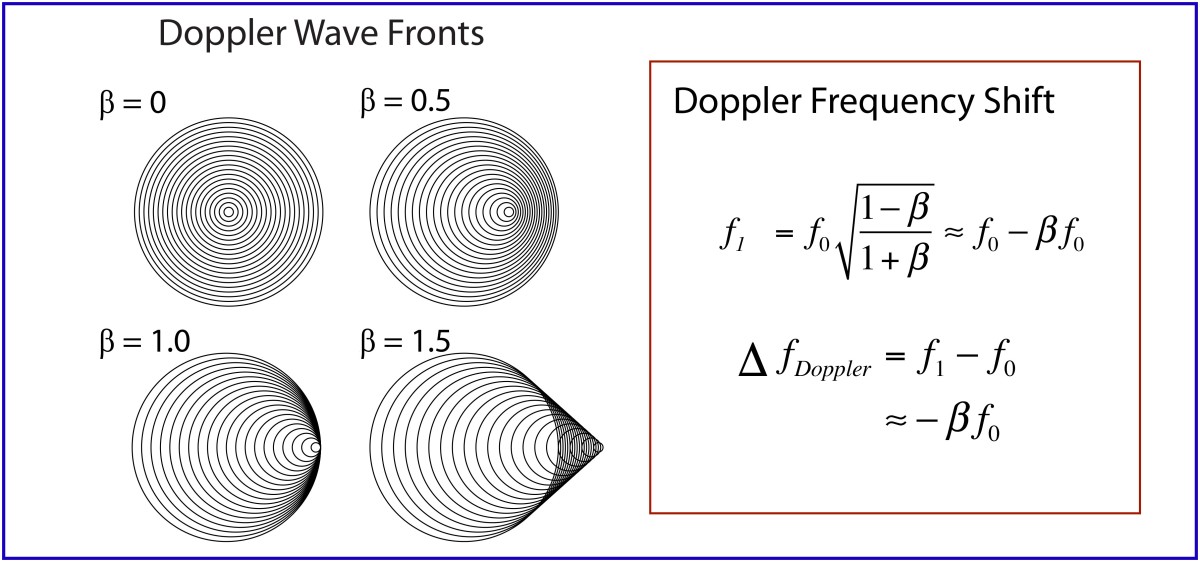
Doppler wave fronts from a source emitting spherical waves moving with speeds β relative to the speed of the wave in the medium.

Doppler calculated the magnitude of the effect by taking a simple ratio of the speed of the observer relative to the speed of light.  What he found was that the speed of the Earth, though sufficient to cause the detectable aberration in the position of stars, was insufficient to produce a noticeable change in color.  However, his interest in astronomy had made him familiar with binary stars where the relative motion of the light source might be high enough to cause color shifts.  In fact, in the star catalogs there were examples of binary stars that had complementary red and blue colors.  Therefore, the title of his paper, published in the Proceedings of the Royal Bohemian Society of Sciences a few months after he read it to the society, was “On the Coloured Light of the Double Stars and Certain Other Stars of the Heavens: Attempt at a General Theory which Incorporates Bradley’s Theorem of Aberration as an Integral Part” [4]. 

Title page of Doppler’s 1842 paper introducing the Doppler Effect.

Doppler’s analogy was correct, but like all analogies not founded on physical law, it differed in detail from the true nature of the phenomenon.  By 1842 the transverse character of light waves had been thoroughly proven through the work of Fresnel and Arago several decades earlier, yet Doppler held onto the old-fashioned notion that light was composed of longitudinal waves.  Bolzano, fully versed in the transverse nature of light, kindly published a commentary shortly afterwards [5] showing how the transverse effect for light, and a longitudinal effect for sound, were both supported by Doppler’s idea.  Yet Doppler also did not know that speeds in visual binaries were too small to produce noticeable color effects to the unaided eye.  Finally, (and perhaps the greatest flaw in his argument on the color of stars) a continuous spectrum that extends from the visible into the infrared and ultraviolet would not change color because all the frequencies would shift together preserving the flat (white) spectrum.

The simple algebraic derivation of the Doppler Effect in the 1842 publication..

Doppler’s twelve years in Prague were intense.  He was consumed by his Society responsibilities and by an extremely heavy teaching load that included personal exams of hundreds of students.  The only time he could be creative was during the night while his wife and children slept.  Overworked and running on too little rest, his health already frail with the onset of tuberculosis, Doppler collapsed, and he was unable to continue at the Polytechnic.  In 1847 he transferred to the School of Mines and Forrestry in Schemnitz (modern Banská Štiavnica in Slovakia) with more pay and less work.  Yet the revolutions of 1848 swept across Europe, with student uprisings, barricades in the streets, and Hungarian liberation armies occupying the cities and universities, giving him no peace.  Providentially, his former mentor Stampfer retired from the Polytechnic in Vienna, and Doppler was called to fill the vacancy.

Although Doppler was named the Director of Austria’s first Institute of Physics and was elected to the National Academy, he ran afoul of one of the other Academy members, Joseph Petzval (1807 – 1891), who persecuted Doppler and his effect.  To read a detailed description of the attack by Petzval on Doppler’s effect and the effect it had on Doppler, see my feature article “The Fall and Rise of the Doppler Effect” in Physics Today, March issue (2020).

Christian Doppler

Voigt’s Transformation

It is difficult today to appreciate just how deeply engrained the reality of the luminiferous ether was in the psyche of the 19^th century physicist.  The last of the classical physicists were reluctant even to adopt Maxwell’s electromagnetic theory for the explanation of optical phenomena, and as physicists inevitably were compelled to do so, some of their colleagues looked on with dismay and disappointment.  This was the situation for Woldemar Voigt (1850 – 1919) at the University of Göttingen, who was appointed as one of the first professors of physics there in 1883, to be succeeded in later years by Peter Debye and Max Born.  Voigt received his doctorate at the University of Königsberg under Franz Neumann, exploring the elastic properties of rock salt, and at Göttingen he spent a quarter century pursuing experimental and theoretical research into crystalline properties.  Voigt’s research, with students like Paul Drude, laid the foundation for the modern field of solid state physics.  His textbook Lehrbuch der Kristallphysik published in 1910 remained influential well into the 20^th century because it adopted mathematical symmetry as a guiding principle of physics.  It was in the context of his studies of crystal elasticity that he introduced the word “tensor” into the language of physics.

At the January 1887 meeting of the Royal Society of Science at Göttingen, three months before Michelson and Morely began their reality-altering experiments at the Case Western Reserve University in Cleveland Ohio, Voit submitted a paper deriving the longitudinal optical Doppler effect in an incompressible medium.  He was responding to results published in 1886 by Michelson and Morely on their measurements of the Fresnel drag coefficient, which was the precursor to their later results on the absolute motion of the Earth through the ether. 

Fresnel drag is the effect of light propagating through a medium that is in motion.  The French physicist Francois Arago (1786 – 1853) in 1810 had attempted to observe the effects of corpuscles of light emitted from stars propagating with different speeds through the ether as the Earth spun on its axis and traveled around the sun.  He succeeded only in observing ordinary stellar aberration.  The absence of the effects of motion through the ether motivated Augustin-Jean Fresnel (1788 – 1827) to apply his newly-developed wave theory of light to explain the null results.  In 1818 Fresnel derived an expression for the dragging of light by a moving medium that explained the absence of effects in Arago’s observations.  For light propagating through a medium of refractive index n that is moving at a speed v, the resultant velocity of light is

where the last term in parenthesis is the Fresnel drag coefficient.  The Fresnel drag effect supported the idea of the ether by explaining why its effects could not be observed—a kind of Catch-22—but it also applied to light moving through a moving dielectric medium.  In 1851, Fizeau used an interferometer to measure the Fresnel drag coefficient for light moving through moving water, arriving at conclusions that directly confirmed the Fresnel drag effect.  The positive experiments of Fizeau, as well as the phenomenon of stellar aberration, would be extremely influential on the thoughts of Einstein as he developed his approach to special relativity in 1905.  They were also extremely influential to Michelson, Morley and Voigt.

 In his paper on the absence of the Fresnel drag effect in the first Michelson-Morley experiment, Voigt pointed out that an equation of the form

is invariant under the transformation

From our modern vantage point, we immediately recognize (to within a scale factor) the Lorentz transformation of relativity theory.  The first equation is common Galilean relativity, but the last equation was something new, introducing a position-dependent time as an observer moved with speed  relative to the speed of light [6].  Using these equations, Voigt was the first to derive the longitudinal (conventional) Doppler effect from relativistic effects.

Voigt’s derivation of the longitudinal Doppler effect used a classical approach that is still used today in Modern Physics textbooks to derive the Doppler effect.  The argument proceeds by considering a moving source that emits a continuous wave in the direction of motion.  Because the wave propagates at a finite speed, the moving source chases the leading edge of the wave front, catching up by a small amount by the time a single cycle of the wave has been emitted.  The resulting compressed oscillation represents a blue shift of the emitted light.  By using his transformations, Voigt arrived at the first relativistic expression for the shift in light frequency.  At low speeds, Voigt’s derivation reverted to Doppler’s original expression.

A few months after Voigt delivered his paper, Michelson and Morley announced the results of their interferometric measurements of the motion of the Earth through the ether—with their null results.  In retrospect, the Michelson-Morley experiment is viewed as one of the monumental assaults on the old classical physics, helping to launch the relativity revolution.  However, in its own day, it was little more than just another null result on the ether.  It did incite Fitzgerald and Lorentz to suggest that length of the arms of the interferometer contracted in the direction of motion, with the eventual emergence of the full Lorentz transformations by 1904—seventeen years after the Michelson results.

            In 1904 Einstein, working in relative isolation at the Swiss patent office, was surprisingly unaware of the latest advances in the physics of the ether.  He did not know about Voigt’s derivation of the relativistic Doppler effect  (1887) as he had not heard of Lorentz’s final version of relativistic coordinate transformations (1904).  His thinking about relativistic effects focused much farther into the past, to Bradley’s stellar aberration (1725) and Fizeau’s experiment of light propagating through moving water (1851).  Einstein proceeded on simple principles, unencumbered by the mental baggage of the day, and delivered his beautifully minimalist theory of special relativity in his famous paper of 1905 “On the Electrodynamics of Moving Bodies”, independently deriving the Lorentz coordinate transformations [7]. 

One of Einstein’s talents in theoretical physics was to predict new phenomena as a way to provide direct confirmation of a new theory.  This was how he later famously predicted the deflection of light by the Sun and the gravitational frequency shift of light.  In 1905 he used his new theory of special relativity to predict observable consequences that included a general treatment of the relativistic Doppler effect.  This included the effects of time dilation in addition to the longitudinal effect of the source chasing the wave.  Time dilation produced a correction to Doppler’s original expression for the longitudinal effect that became significant at speeds approaching the speed of light.  More significantly, it predicted a transverse Doppler effect for a source moving along a line perpendicular to the line of sight to an observer.  This effect had not been predicted either by Doppler or by Voigt.  The equation for the general Doppler effect for any observation angle is

Just as Doppler had been motivated by Bradley’s aberration of starlight when he conceived of his original principle for the longitudinal Doppler effect, Einstein combined the general Doppler effect with his results for the relativistic addition of velocities (also in his 1905 Annalen paper) as the conclusive treatment of stellar aberration nearly 200 years after Bradley first observed the effect.

Despite the generally positive reception of Einstein’s theory of special relativity, some of its consequences were anathema to many physicists at the time.  A key stumbling block was the question whether relativistic effects, like moving clocks running slowly, were only apparent, or were actually real, and Einstein had to fight to convince others of its reality.  When Johannes Stark (1874 – 1957) observed Doppler line shifts in ion beams called “canal rays” in 1906 (Stark received the 1919 Nobel prize in part for this discovery) [8], Einstein promptly published a paper suggesting how the canal rays could be used in a transverse geometry to directly detect time dilation through the transverse Doppler effect [9].  Thirty years passed before the experiment was performed with sufficient accuracy by Herbert Ives and G. R. Stilwell in 1938 to measure the transverse Doppler effect [10].  Ironically, even at this late date, Ives and Stilwell were convinced that their experiment had disproved Einstein’s time dilation by supporting Lorentz’ contraction theory of the electron.  The Ives-Stilwell experiment was the first direct test of time dilation, followed in 1940 by muon lifetime measurements [11].

---

Further Reading

D. D. Nolte, “The Fall and Rise of the Doppler Effect“, Phys. Today 73(3) pg. 30 (March, 2020)

D. D. Nolte, Interference: The History of Optical Interferometry and the Scientists who Tamed Light (Oxford University Press, 2023)

---

Notes

[1] pg. 15, Eden, A. (1992). The search for Christian Doppler. Wien, Springer-Verlag.

[2] pg. 30, Eden

[3] Bradley, J (1729). “Account of a new discoved Motion of the Fix’d Stars”. Phil Trans. 35: 637–660.

[4] C. A. DOPPLER, “Über das farbige Licht der Doppelsterne und einiger anderer Gestirne des Himmels (About the coloured light of the binary stars and some other stars of the heavens),” Proceedings of the Royal Bohemian Society of Sciences, vol. V, no. 2, pp. 465–482, (Reissued 1903) (1842).

[5] B. Bolzano, “Ein Paar Bemerkunen über die Neu Theorie in Herrn Professor Ch. Doppler’s Schrift “Über das farbige Licht der Doppersterne und eineger anderer Gestirnedes Himmels”,” Pogg. Anal. der Physik und Chemie, vol. 60, p. 83, 1843; B. Bolzano, “Christian Doppler’s neuste Leistunen af dem Gebiet der physikalischen Apparatenlehre, Akoustik, Optik and optische Astronomie,” Pogg. Anal. der Physik und Chemie, vol. 72, pp. 530-555, 1847.

[6] W. Voigt, “Uber das Doppler’sche Princip,” Göttinger Nachrichten, vol. 7, pp. 41–51, (1887). The common use of c to express the speed of light came later from Voigt’s student Paul Drude.

[7] A. Einstein, “On the electrodynamics of moving bodies,” Annalen Der Physik, vol. 17, pp. 891-921, 1905.

[8] J. Stark, W. Hermann, and S. Kinoshita, “The Doppler effect in the spectrum of mercury,” Annalen Der Physik, vol. 21, pp. 462-469, Nov 1906.

[9] A. Einstein, “”Über die Möglichkeit einer neuen Prüfung des Relativitätsprinzips”,” vol. 328, pp. 197–198, 1907.

[10] H. E. Ives and G. R. Stilwell, “An experimental study of the rate of a moving atomic clock,” Journal of the Optical Society of America, vol. 28, p. 215, 1938.

[11] B. Rossi and D. B. Hall, “Variation of the Rate of Decay of Mesotrons with Momentum,” Physical Review, vol. 59, pp. 223–228, 1941.