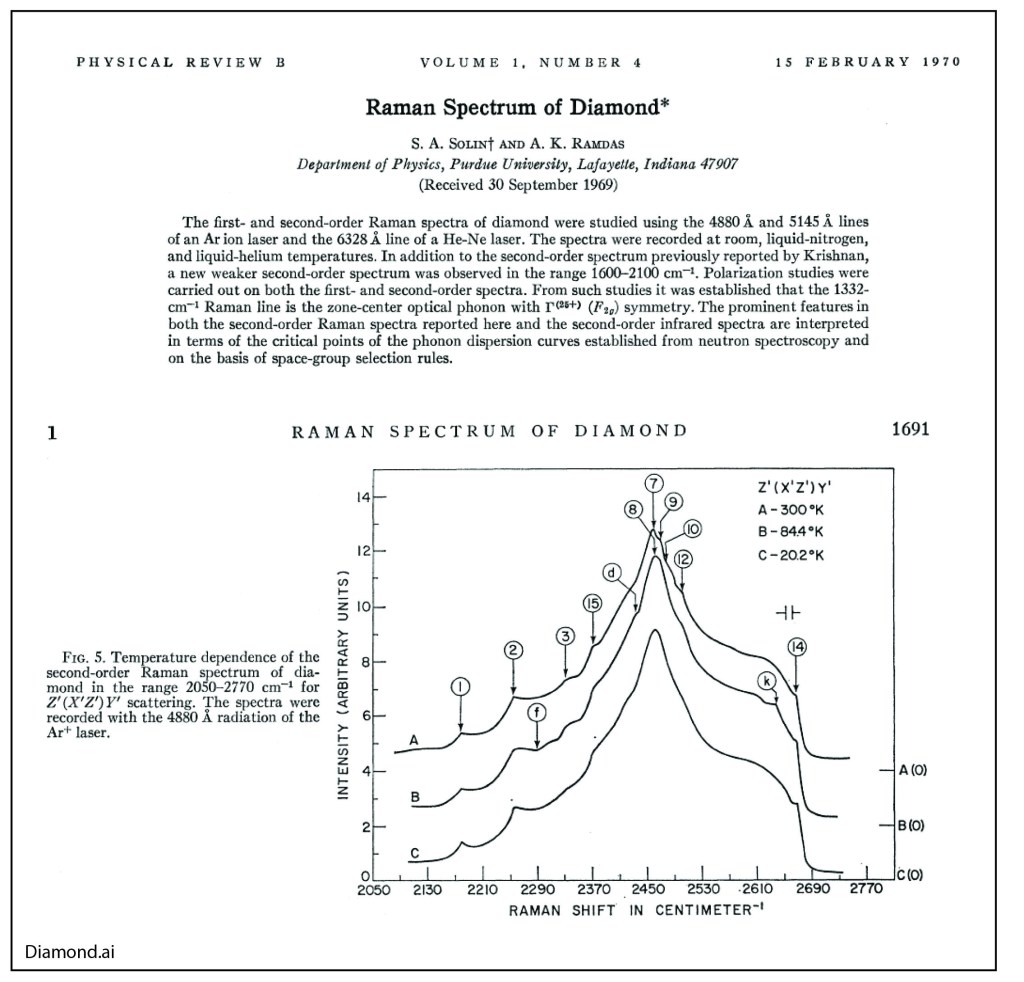
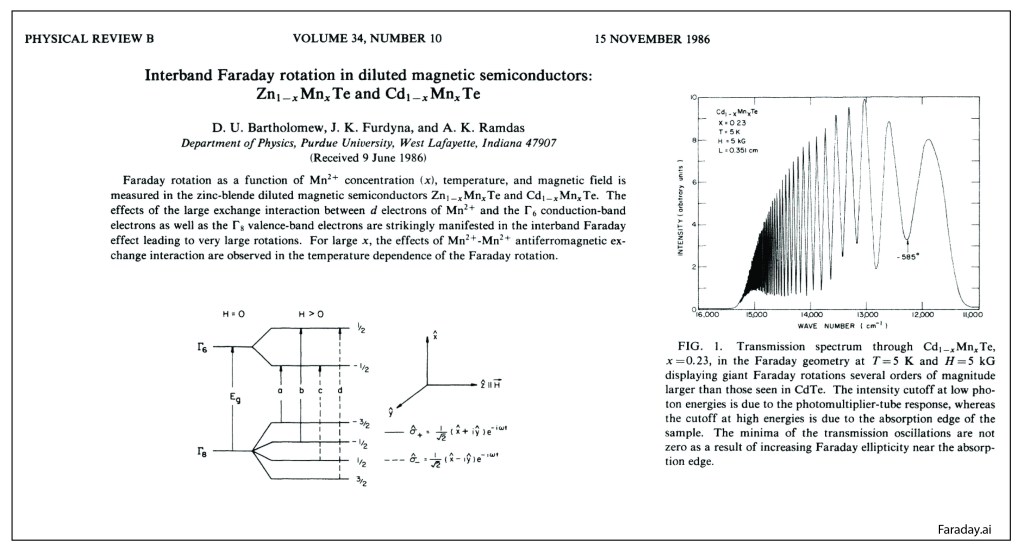
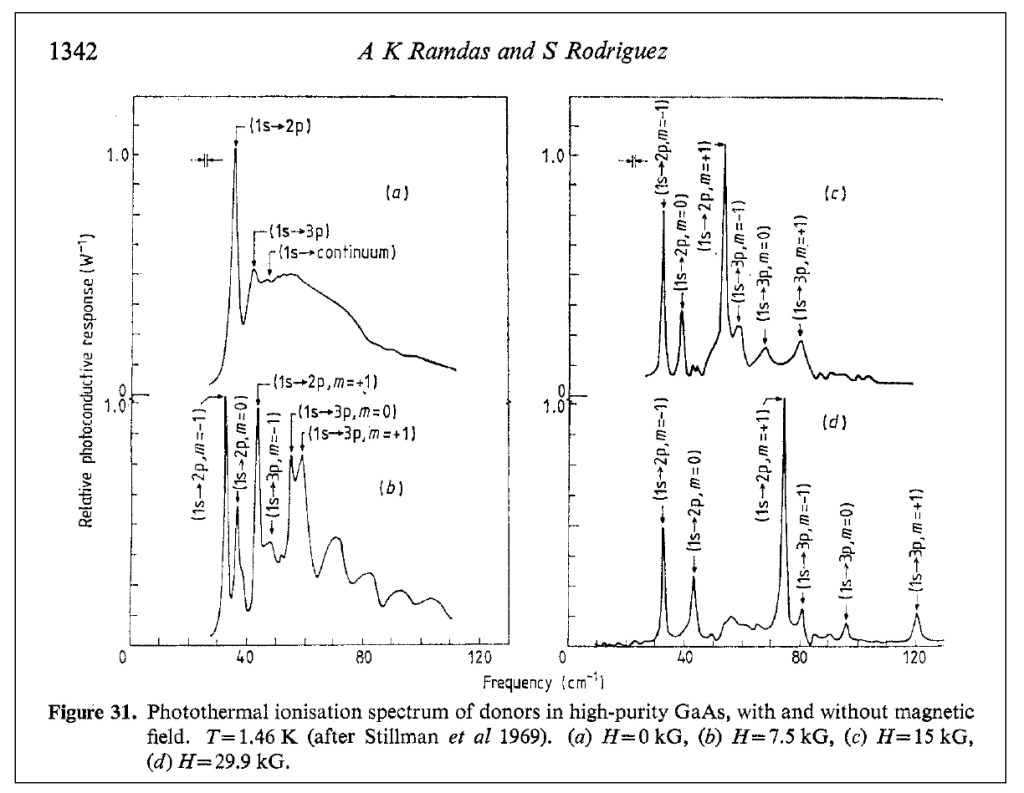
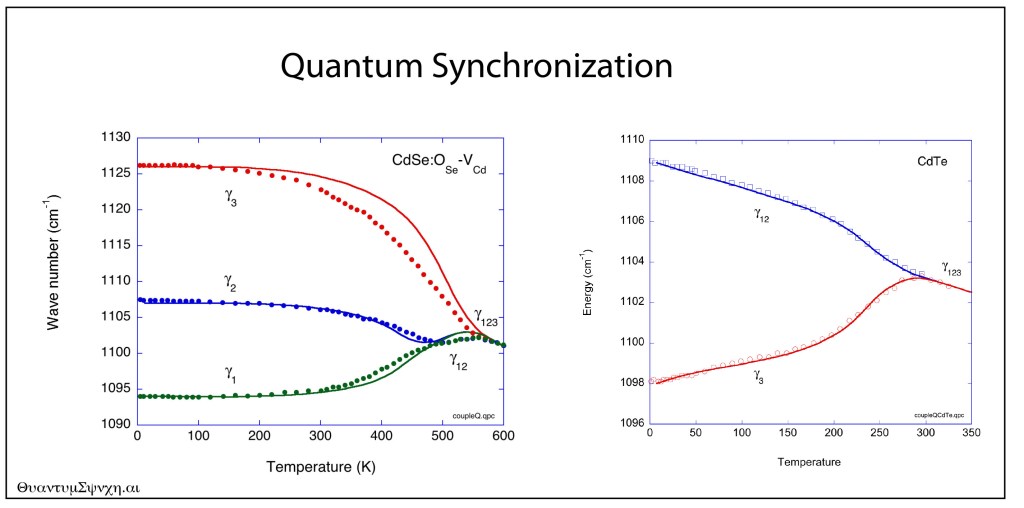
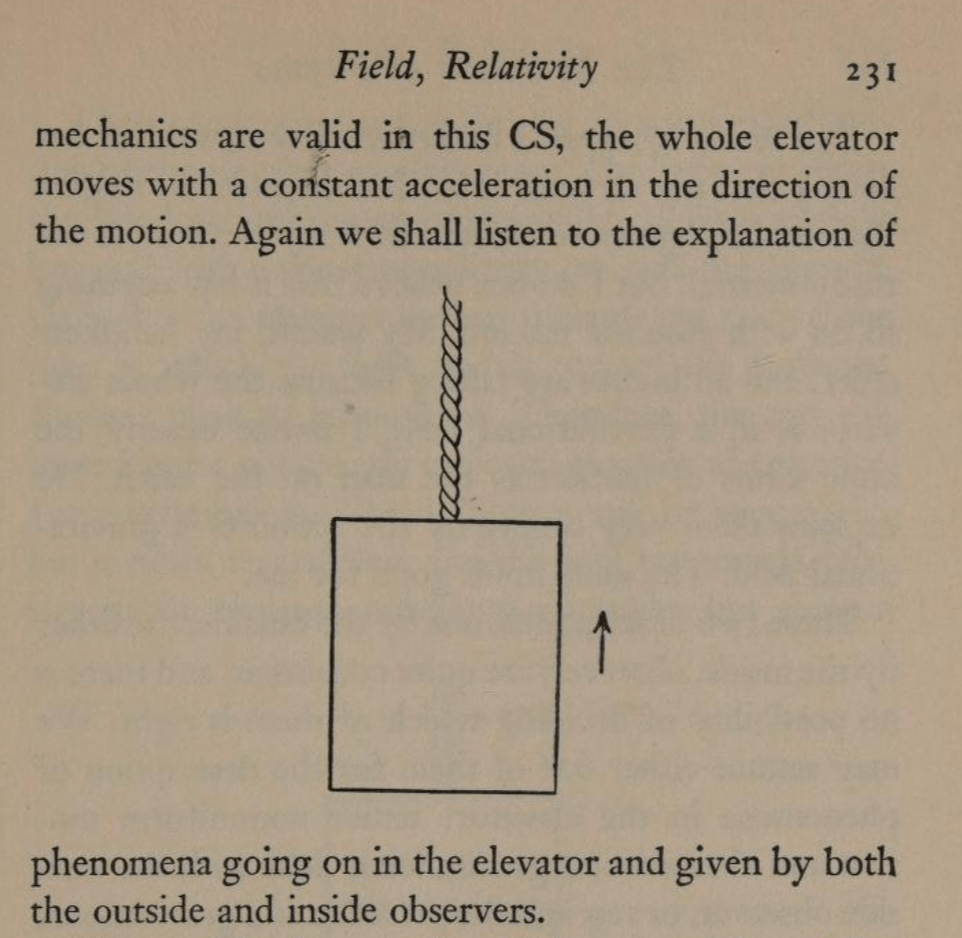
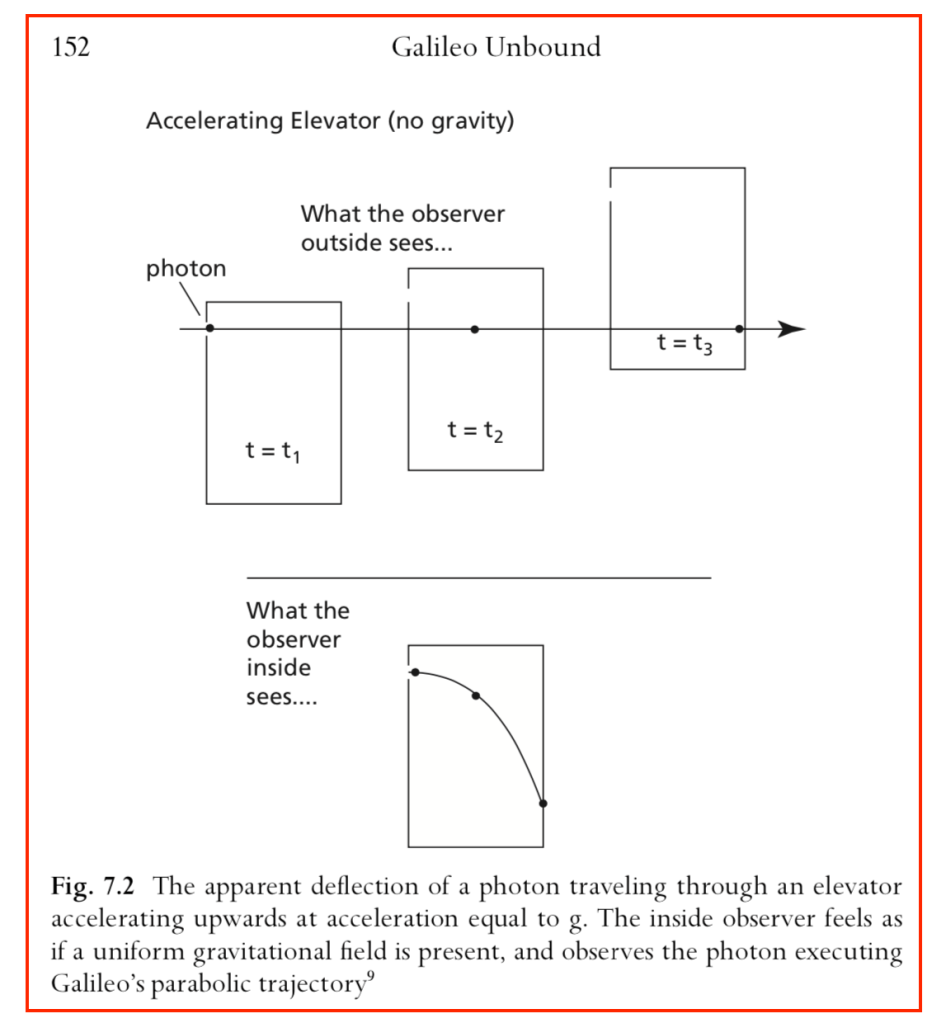
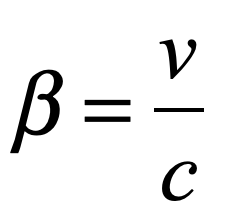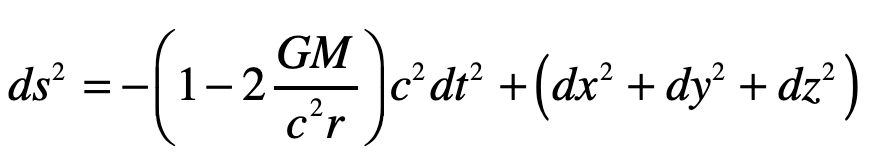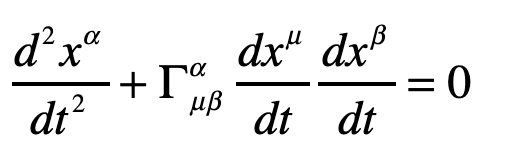Roger Bacon and his Opus Majus
by David D. Nolte

Roger Bacon and the Art of Grant Proposal Writing

It’s amazing what a little house arrest can do for the active mind. It provides time and focus as well as protection from earthly distractions that dissipate the intellect. How much more productive might we be if freed from the daily grind?

For Galileo Galilei, house arrest after ridiculing the pope gave him time to write his “Two New Sciences” that had been percolating in the back of his mind for decades. His arrest gave birth to the sciences of mechanics and strength of materials.

For Augustin Fresnel, house arrest after supporting royalists against Napoleon was the perfect retreat from building roads and bridges to explore the physics of light scattering and interference. His arrest gave birth to the physics of optical interference.

For Jean-Victor Poncelet, whiling away his time as a prisoner of war in Russia after Napoleon’s disastrous march on Moscow, it kept him occupied and sane. His confinement gave birth to the theory of projective geometry.

For Piotr Kapitsa, exiled under Stalin for not joining the Party, he could focus on his physics. His arrest gave birth to the physics of dynamic equilibrium.

For Roger Bacon (121? – 1292), the medieval Franciscan friar who was under effective house arrest (his monastic cell) and prohibited from publishing anything, his arrest gave birth to the first science grant proposal.

The Rise of Roger Bacon

More has been written about Roger Bacon that is fantasy than the truth. In truth, almost nothing is known of his background, other than that he came from a wealthy family. They paid for him to go to college, at the age of thirteen, at Oxford, where he studied until he received his magister’s degree around 1240. Because Oxford was a religious college, his degree allowed him to teach anywhere under the umbrella of the Catholic Church, whether in Bologna, Rome, Paris or Oxford. Latin was the universal language, and the Christian faith was the universal context of all the young universities, so that scholars could move at will among these great centers of learning, despite the constant wars that raged between England and France. Bacon began teaching at Oxford, but the university in Paris at that time removed their prohibition against the teaching of Aristotle’s science, so he was recruited in 1241 to teach science in the Faculty of Arts, in the English division of the University of Paris.

During his time in Paris, across seven years, starting when he was around 30 years old, he began to shift his perspective on the state of learning in the university system. At that time, scholarly discourse was based on creative citation of the authorities, much like discourse is in law, citing court cases and legal precedence. New ideas arose by finding ambiguities or contradictions in established texts and then arguing for a new theory that could explain or contain formerly conflicting points of view. This kind of learning was endlessly self-referential and backwards focused, never moving forward beyond the frontiers of what was known.

At Paris, he met Peter Peregrinus, whose open-mindedness came as a revelation to Bacon. Peregrinus was willing to study anything, no mater how arcane (even magic tricks), burrowing down to the finest detail to understand how it worked. This meant using direct observation in place of cited authorities as the foundation for creating new ideas that could explain what was observed. At the time this was a radical departure, because it meant that the realm of knowledge could be added to, not just refined. It also elevated the individual to the level of the ancient authorities in their ability to devine new truths about nature. These new attitudes about observation and experimentation were reinforced when Bacon returned to Oxford in 1247 where he was exposed to the ideas of Robert Grosseteste.

Grosseteste and Bacon at Oxford

Robert Grosseteste (1170 – 1251) was born poor but his brilliance must have been recognized early by some priest with influence, because his education was supported by the Church. He was educated at Oxford and began teaching there, rising through the ranks to become the Magister Scholarum (Master of the Schools … like Chancellor) of Oxford University in 1215, a position he held for six years. This high office allowed him a latitude of thought that would have been impossible in a lesser position, and he slowly changed the mindset at the university away from the verbal arguments of Scholasticism.

Teaching at Oxford focused on the quadrivium (geometry, arithmetic, music, and astronomy), which was not “science” as we would understand it today, but it had some of the ingredients. Grosseteste emphasized the importance of observation of nature to test theoretical predictions, and he enlisted geometry and arithmetic as tools to describe observations. These both were innovations over the previous Scholastic emphasis of pure reason divorced from direct experience (eperimentum). Grosseteste’s favorite topic for observation and experience was the natural behavior of light and optics, in part because the behavior of rays of light could be captured using geometry.

Grosseteste stepped down from the chancellory in 1221 to teach at Franciscan monasteries that were closely associated with university life. He was still teaching there at the time when Bacon entered Oxford, but it is not known if they ever had an association. By the time Bacon returned to Oxford in 1247, Grosseteste had moved on to become the Bishop of Lincoln, but his legacy of natural philosophy was firmly embedded in the mindset of the faculty teaching the quadrivium.

After arriving back at Oxford, Bacon embraced Grosseteste’s teachings and began systematically expanding on them. From Grosseteste, he adopted the need to validate theory by direct experience, to use of mathematics to describe phenomena, and he chose the study of light and optics as the prime example of the new approach. He used his access to his family’s wealth to buy an extremely large assortment of books and tables and instruments. The value of these purchases today would be in the range of a million dollars or so; it was a vast collection of academic value. He was an independent scholar, and independently wealthy, so it is hard to understand why, a few years later in 1251, he joined the Franciscan Order with its vow of severe poverty.

It may have been Grosseteste’s association with the Franciscans (although Grosseteste never joined the order himself), or the close association of the Franciscans with higher learning. It may also have been because Bacon was accumulating enemies as he pushed Grosseteste’s ideas to more radical extremes. Bacon was known to be arrogant and caustic, and his willingness to entertain new ideas, possibly going against traditional Church doctrine, was putting him more at risk at a time when deviating from doctrine could be physically dangerous. Joining the Franciscans might have been a sort of protection for him, though he would have had to give up his collection of books, tables and instruments because of the poverty vow. At first, this seemed a shrewd move, but in time it unravelled into a personal nightmare.

Statue of Roger Bacon at Oxford

Roger Bacon in Crisis

The Church has always been buffeted by the persistent emergence of heresies against doctrine, and it always has worked to stamp them out. Around the time of Bacon, the most dangerous heresy was Joachimism, or the heresy of the Eternal Gospel. It had strange ideas about the Apocolypse that did not sit well with Church teachings, so it was aggressively banned. Unfortunately, many Franciscan academics were in the thick of it, and they were also in a position to publish books about it. In 1256, only 5 years after joining the Franciscan order, the new leader of the order banned writing on any unsanctioned topic, trapping Bacon with no publishable outlet for his ideas. But that didn’t stop him from talking.

In 1264, the French lawyer and diplomat Cardinal Guy de Foulques was in England to mediate between Henry III and his barons who were on the edge of revolt over Henry’s abuse of power. During a quiet period in the negotiations, Bacon and de Foulques met and talked. It was a rare outlet for Bacon who had been pent up for years. He impressed de Foulques with his wide-ranging ideas about education reform to move beyond the stagnation of Scholasticism. Bacon argued for an emphasis on science and math as a way to uncover natures secrets, and he promoted the learning of languages (Arabic and Hebrew and Greek) to better learn from all the intellectual output of other cultures. It must have been a heady conversation, and Bacon was probably thrilled to have such an esteemed listener. But his own life was poised on disaster.

Three events collapsed Bacon’s world around him. First, despite de Fulques efforts, negotiations broke down and the Second Baron’s War broke out. Second, Bacon’s wealthy family supported the king but were overrun by the Barons and ruined. Third, Bacon and his ideas were now deemed too dangerous by his Franciscan superiors, and he was sent to a convent outside of Paris in effective house arrest as his days were filled with menial tasks purposely meant to exhaust him and give him no time to think.

One year into the war and into Bacon’s exile to Paris, Cardinal de Fulques was elected pope as Clement IV. He took up the mantel of Christ just as Christianity was in retreat on multiple fronts. In the northeast it was under assault by the terrifying and highly successful Mongol invasion, in the southwest by a military incursion into Spain from Moorish Morroco, and in the Levant by the Mamluk Sultanate as they recaptured the last Christian outposts from the Crusades. Clement needed help, and he never forgot his conversation with Bacon about how to use science and math to give the Christian forces the upper hand. At the time of their talk, Bacon had been so persuasive while pitching his ideas so hard, that Clement had walked away with the impression that it was all already written up. So he sent a letter to Bacon in Paris asking for an immediate report on the status of Bacon’s program. That letter was a trigger for one of the most astounding bursts of creative scholarship of the Middle Ages. It was also the trigger for what may be called the first scientific grant proposal.

Roger Bacon’s Opus

When the Pope’s letter arrived in Paris, Bacon was ten years into the Franciscan prohibition against publishing and two years into his sentence of menial labor. To respond to the Pope’s request was both a dream and nightmare. It was a dream, because it gave Bacon the ear of the most powerful person in Europe and an outlet for all his pent up ideas. It was a nightmare, because he had no time to do the work and no resources to accomplish it.

To create a manuscript in the 13th century was a long and expensive process that required funds to buy materials. His family had just been ruined financially in the Baron’s war, so he secretly turned to friends to help support the project. He also worked mostly at night while spending his days on all his duties at the convent.

His central thesis was clear: Christian forces were in retreat because their enemies had both technological and logistical superiority. To gain the upper hand in the fight required a reform of teaching across Europe. By better understanding the laws of nature through math and science, they could develop technologically superior weapons. By better understanding languages, they would have access to learning from other cultures. By better understanding moral philosophy, they would gain the advantage of the moral high ground.

To show how to put these ideas into practice, Bacon chose specific examples. He picked the study of optics (perspectiva) as a way to practice detailed observation and mathematical description of physical phenomena. He promoted the questioning of authority as a way to escape the ruts of old thinking, opening the mind to new possibilities. He championed astronomy and calendar reform to stop the seasons from drifting across the years and to improve logistic planning. He supported geography as a way to better understand where future threats might emerge.

Roger Bacon’s optical studies.

In a little over one year, Bacon wrote four manuscripts that contained nearly a million words in total. To put that in perspective, a typical academic book published today has about 100,000 words. Therefore, Bacon wrote in one year the equivalent of about 10 academic books at a time without word processors and without paper, all written by hand in permanent ink on expensive parchment. This output was put into three works — the Opus Majus, the Opus Minus and the Opus Tertium — plus a fourth manuscript that was the first of its kind: the grant proposal.

The Letter on the Secret Works of Art and Nature

The primary purpose of Bacon’s response to the Pope was to ask him to fund research. The Opus, despite its massive size, was simply an outline that needed to be filled in, an activity that required time and money and freedom (as a way to escape his house arrest). Bacon was approaching the age of 50 and his time was running out. Life expectancy for someone who survived childhood in the 13th century was only about 55 years.

To clearly communicate the urgency of his program and the advantages that could be gained by adopting it, Bacon wrote Epistola de Secretis Operibus (Letter on the Secret Works of Art and Nature). He took out all the stops and let his imagination run free to describe what might be possible with applied physics.

Bacon envisioned machines that would move mechanically across land or water without the need for human power (automobiles and ships). He suggested other machines that could move secretly under water to surprise an enemy (submarines). He even imagined machines that could transport a man through the air, speeding him across a battlefield (airplanes). From the study of optics, he proposed the ability to make far things appear close (telescopes). From the study of mechanics, he envisioned bridges that could span great distances (suspension bridge), and systems that could support weights much larger than could be lifted by man (mechanical and civil engineering). And he gave the formula for a chemical mixture that could destroy the walls of cities (gunpowder).

The letter reads like the classic section of a grant proposal that lists potential benefits. He may have been looking far into the future, much farther than we do now when we write modern grant proposals, but his reasoning was surprisingly sound, based on the knowledge that would be gained by studying the laws of nature, i.e., science.

Unfortunately, shortly after Bacon secretly delivered his works to the Pope through a trusted student, the Pope died, possibly never having read any of it. Worse, Bacon was later imprisoned in Italy, placed in solitary confinement for ten years because of fear of his radical ideas. He was finally released, around the age of 80, never having accomplished his grand program. He died two years later at his beloved Oxford.

Discoveries in physics in the first quarter of the 21st Century.
by David D. Nolte

The Best Physics of the Century (So Far)

Our century is now a quarter complete, from Y2K to today (2000 – 2025).  What have been the greatest discoveries in Physics so far? And what do they portend for the rest of the century?

Every century of physics tends to have its own character:

• The 1600’s were the time of Galileo, Descartes, Huygens, Leibniz and Newton who created the science of dynamics out of nothing. 

• The 1700’s were the time of du Chatelet, Maupertuis, Euler, Lagrange, and D’Alembert who constructed mathematical physics on the foundation of the calculus. 

• The 1800’s were the time of Young, Fresnel, Hamilton, Maxwell, Boltzmann, and Lord Kelvin who completed the program of classical physics. 

• The 1900’s were the time of Einstein and Bohr who invented relativistic and quantum physics and launched the grand program of unified forces.

Now we come to the 2000’s. What will this century be known for?

Two topics physicists have at the top of their mind today is Quantum and AI (and there is even quantum AI).  But AI is merely a tool (though an important one that is radically changing how physics is done), and quantum is a catch-all (almost everything is quantum at its core).

So, what are the greatest breakthroughs of the 21st Century so far?  And what do they portend for the eventual “character” of 21st-Century physics when seen in the rear-view mirror of history by the year 2100?

Single-photon Quantum Information (2001)

The century started on July 24, 2000, when a landmark paper was received by Nature magazine submitted by Emanuel Knill and Raymond Laflamme at Los Alamos National Lab in the United States with Gerald Milburn from the University of Queensland, Australia (collectively known as KLM). This little-heralded paper proposed a radical new idea in quantum information, an idea that would have profound effects on the development of quantum science for the coming quarter-century.

The idea was simply that quantum logic could be performed with single photons and linear optics [1]. Up to that point, most research on quantum optical computing was trying to get photons to interact with each other (which they really don’t like to do) in nonlinear media like crystals or trapped atoms. What KLM showed was that quantum information could be manipulated in general ways without interactions. The paper proposed a technique that could perform quantum logic in a universal way using only linear optical elements like single-photon sources, beam splitters, phase shifters, and single-photon detectors, introducing the novel idea of “measurement-based” quantum computing.

Recovery from Z Linear Optical Quantum Computing
Fig. 0. LOQC circuitry from the KLM paper.

In the quarter-century since the publication of the KLM paper, LOQC has steadily progressed via the development of single-photon sources and detectors. Today, numerous start-ups are pursuing LOQC, notably Xanadu in Toronto, Canada, and PsiQuantum in Palo Alto, USA and Brisbane, Australia. By 2100, this century will likely be viewed as the time when applications of quantum information reached their maturity.  Where the 20th century was a century of discovery of quantum phenomena, the 21st will be the century when it was reduced to practice.

Solar Neutrino Oscillation (2001)

The sun is fueled by the fusion of hydrogen that generates electron neutrinos. The reaction looks like

where p is a proton (hydrogen), 2H is deuterium (a hydrogen nucleus with an extra neutron), e+ is a positron (the anti-matter form of an electron) and ν e is an electron neutrino. This reaction accounts for 99% of the neutrinos generated by the Sun, calculated by the theoretical astrophysicist John Bahcall of the Institute for Advanced Study at Princeton University. Already by the late 1960’s it was suspected that too few of the neutrinos were being detected compared to predictions, so he teamed with Raymond Davis of Brookhaven National Lab to build an experiment to detect the flux of solar neutrinos. To shield the detector from cosmic rays, the experiment was placed at the 4850 level of the Homestake Gold Mine in Lead, South Dakota and operated from 1970 to 1994. The deficit of solar neutrinos was confirmed, and it was huge: Fully two-thirds of expected solar neutrinos were missing!

The simplest solution to the missing solar neutrinos was that they just weren’t there because, on their way to Earth from the Sun, they had converted to something else that was not detectedable. This conversion from one particle to another is possible if neutrinos have a non-zero (but extremely small) mass. If so, then an electron neutrino can convert to a muon neutrino, and if the distance is far enough, they can convert back. In other words, the nature of the neutrino particle is that its identity oscillates. This is called the solar neutrino oscillation, and by the time the neutrinos have arrived at Earth, two-thirds of them have converted to muon neutrinos.

There was a general reluctance to accept neutrino oscillations because it represented a departure from the Standard Model of particle physics and introduced uncomfortably small masses for neutrinos that otherwise behave like massless particles. Two experiments put these qualms to rest: the Super-Kamiokanda expeeriment in Japan and the Sudbury Neutrino Oscillation experiment in Canada. By the early years of the century, neutrino oscillations had been confirmed.

Neutrino oscillations
Fig. 1. Electron neutrinos (black) convert to muon (blue) and tau (red) neutrinos as a function of distance relative to their energy. The value of L/E for solar neutrinos and the Earth is much larger than plotted here, so the effects average out to a net deficit of electron neutrinos. From Ref.

By 2100, the mystery of the ultra-small neutrino masses will likely have been solved.  If the answer falls within the Standard Model, then this may be the crowning achievement that “completes” the standard model.  If the answer falls outside the Standard Model, then this may be the beginning of a new chapter in high-energy physics.

WMAP and Planck (2003)

The Big Bang may have occurred 13.7 billion years ago, but that Bang echoes to this day across the Universe. At its inception, the reverberations were incredibly hot, but they have cooled now to a mere 3 degrees Kelvin. In 1987, Paul Richards and Andrew Lange at the University of California at Berkeley, recorded the peak of the Planck black body spectrum during a sounding rocket flight that carried a far-infrared spectrometer to the edge of space. (The dichroic bandpass filters in their spectrometer were the first far-infrared metamaterials. I designed and built them as a young grad student at Berkeley! [2]) This experiment was followed by the COBE satellite that measured the presence of minuscule fluctuations in the temperature, representing the original heterogeneity of the universe just after the Big Bang.

COBE flew for a year, followed in 1998 by the BOOMerAng experiment, led by Andrew Lange, that was suspended from a high-altitude balloon circling the South Pole for ten days. This experiment discovered the literal echoes of the Big Bang, acoustic oscillations, in other words, the “sound” of the Bang. It also established that the universe is gravitationally “flat”, which is a direct consequence of cosmic inflation. Once again, these findings were followed by a satellite experiment, the WMAP mission in 2003, that mapped these oscillations over the entire sky. Even finer resolution was obtained by the Planck mission in 2013, measuring higher harmonics of the sound oscillations. These oscillations in the early universe helped seed regions of slightly higher density that condensed into galaxies, leading to the large-scale structure of the universe that we see today.

Anisotropy of the cosmic background radiation
Fig. 2. Successively higher resolution views of the echos of the Big Bang from COBE (1992) to WMAP (2003) to Planck (2013). From Ref.

The 21st Century will likely be known as the time when the physics of the early universe was finally pinned down, and maybe even of what can before. The answers may tell us if there are parallel universes in a much larger metaverse.

Exoplanets (2009)

The Earth is not alone in the Universe. It is not even alone in our little neighborhood of the Milky Way. Within 50 light years it is estimated that there are about 1000 Earth-sized planets in the habitable zone of their respective stars. Why is 50 light years significant? It is because, within this century, the technology to explore those planets is likely to be developed. With the right designs, an unmanned probe could reach 50 light years from Earth within a century, and the time to call back home is only 50 years. So if a probe is launched in the year 2100, we could be receiving transmissions from the new planet by the year 2250.

This estimate of 1000 New Earths is the result of a quiet revolution in planetary science that has been unfolding over the past quarter century. The very first exoplanet was confirmed in 1995 by Michel Mayor and Didier Queloz. Today, as of the writing of this blog, there are 6,278 confirmed exoplanets. Most of these were disovered by the Kepler satellite that was launched in 2009.

Kepler exoplanet discoveries
Fig. 3. An artists rendition of several of the Earth-sized planets discovered by the Kepler satellite. From Ref.

By 2100, we will know where all the exoplanets are that are within 50 light years of Earth, and we will know which ones are potential inhabitable.  It may even happen that signs of life on one of these planets will have been discovered.  If so, then it is hard to imagine humankind NOT launching probes to visit those planets.  If the right propulsion technology is developed, then those probes could be signaling back information from those planets as early as the year 2250…if anyone is still here to listen.

The Higgs (2012)

The crowning achievement of high-energy physics may also have been the last nail in the coffin. Throughout the second half of the 20th century, high-energy physics took the lion’s share of money and attention showered on physics. Beginning in the aftermath of the Manhattan Project, the search for the fundamental constituents of our universe at first found more and more particles, creating a “zoo” that resisted easy classification, until quarks were proposed that simplified the whole thing down into what is now called the Standard Model of Physics.

But one piece of the puzzle was still missing–the explanation of why particles have the masses they do. This missing piece was supplied by the theoretical physicist Peter Higgs in 1964 who proposed that point-like massless particles interacted with a “field” that permeated space. The interaction energy was equivalent to mass through Einstein’s famous E = mc2, and the quantization of the field predicted the existence of a “Higgs Boson”. The search for the “Higgs”, as it is called for short, became the Holy Grail of Physics at the end of the last century.

Higgs production, decay and pair processes as Feynman diagrams
Fig. 4. Feynman diagrams that involve the generation of Higgs particles.

The discovery of the Higgs boson was announced on the 4th of July in 2012 [3]. It capped 80 years of progress in high-energy particle physics since the discovery of the positron in 1932. But it may also be the last. Since 2012, over the past 14 years, there have been no new “major” discoveries at the Large Hadron Collider (LHC). Most high-energy talks since then have been about speculative experiments seeking deviations from the Standard Model, but so far there is nothing new.

In the year 2100, looking back, the era of high-energy physics may be relegated to the 20th century, with the Higgs just a finishing touch that tipped over into the new millennium … Or sometime in the next 75 years there will be a discovery that goes beyond standard physics and opens a new chapter in the field. We will have to wait to see.

Gravitational Waves (2015)

Where were you on Nov. 11, 2015 at 10:30 am? Can you remember? I can! I was in a conference room in the Physics Building on the Purdue University Campus waiting with a small crowd of physicists for a news conference to begin. Everyone knew it would be something big. It was. They announced the first detection of a gravitational wave by the LIGO detector (the Laser Interferometric Gravitational Wave Observatory). In a way, it was anti-climactic because we all knew that LIGO would eventually see one. But it was also immensely dramatic, because it was the most sensitive measurement ever made by mankind. The displacement of the mirrors in the interferometer caused by the passing gravitational wave was a tiny fraction of a radius of a proton, yet the signal was as clear as a bell. It came from the merger of two 30 solar-mass black holes in a galaxy far, far away.

First detection of gravitational waves by LIGO
Fig. 5. The two LIGO recordings (at Hanfored and at Livingston) of the first detected gravitaitonal wave. From Ref.

By the year 2100, looking back, multi-messenger astronomy will have been a key part of the physics of the 21st century. Multi-messenger astronomy is when an astronomical event is detected across many detection modes, possibly including light, infrared, ultraviolet, x-ray, neutrino and gravitational wave detection. The field is just beginning and has a long way to go to integrate all these different ways of seeing into a complete picture of what happens out in the universe.

Topological physics (2016)

Of all the topics of this blog, this one is perhaps the most abstract. When we think of geometry, it is natural to think in terms of the symmetries that objects have. The last century was the pinnacle of geometric physics, where Einstein showed that gravity is a geometric property of warped space, where group theory classified all the ways that objects can be constructed and behave, and symmetry breaking was invoked to explain the hierarchy of physical forces.

The new century will be the time of topological physics, where symmetries of matter may not even matter, but the way that properties of matter are connected does. By “property of matter” I mean like the electronic states of a solid state material where the states are excluded from portions of state space, creating topology in abstract spaces. Such topological properties govern how freely currents can flow on surfaces but not in the bulk, or vice versa. In quantum systems, topological properties can protect quantum information from decoherence, which is the bane of most real-world implementations of quantum computers. For instance, by “braiding anyons” it is possible to create qubits that resist dephasing.

Braided anyons at Purdue
Fig. 6. Evidence for the braiding of anyons in the solid state. From Ref.

The importance of topology in physics was recognized with the 2016 Nobel Prize to David J. Thouless, F. Duncan M. Haldane, and J. Michael Kosterlitz for “Theoretical discoveries of topological phase transitions and topological phases of matter.”

Images of Black Holes (2019)

Why hasn’t this gotten a Nobel Prize yet? The imaging of black holes is a tour de force, requiring a telescope with the diameter of a planet, and requiring the collaboration of scientists from across that planet to make it all work.

The physics is straightforward. Everyone knows that bigger telescopes have better resolution, so the logical limit is a telescope the size of the Earth. This is accomplished by using interferometric detection, with data from widely spread millimeter-wave telescopes synchronized by an atomic clock in a network of telescopes known as the Event Horizon Telescope (EHT). The results are constructed numerically, as shown below.

Event Horizon Telescope (EHT) images of a black hole

Fig. 7. The EHT images (left) compared to the model (middle) and the blurred model (right) of the black hole in the M87 galaxy. From Ref.

The next logical step for this kind of imaging is a telescope array that is bigger than the Earth … much bigger! This could be accomplished with an array of Lagrange-point satellites, improving the resolution of the images. By the end of this century, we may be imaging the black holes in all the near-by galaxies.

More to Come?

What are the greatest outstanding problems of physics that may yet yield to solutions within this century? It is impossible to say for certain without a crystal ball, but there are some that are likely to be resolved in the next 75 years:

• Dark Matter: This is the 500 pound gorilla in the room. If most of the tangible universe is made of this stuff, then we had better get around to detecting it!

• Dark Energy: This is the other 500 pound gorilla in the room. If most of the intangible universe is made of this stuff, then we had better get a good understanding of it.

• Quantum Gravity: Of the four forces of physics (gravity, electro-magnetic, weak nuclear and strong nuclear) gravity stands apart in several ways, one of which is that there is no quantum theory for it. We have 75 years to fix this if it is to be a crowning achievement of 21st-Century physics.

• The Evolution of Life: I didn’t include any biophysics in my list of the best physics of the century mainly because I cannot point to a single revolutionary breakthrough of physics in this area. There has been a lot of good progress on the microphysics of biological systems, but nothing like discovering a Higgs boson. This could change if the origins of life turn out to be physics-based rather than just some chemistry.

• The Evolution of Intelligence: I think physics has more to say on the evolution of intelligence than on the evolution of life. Intelligence is the quintessential complex system, and the methods of theoretical physics may yet provide a clear answer to the question of “What is Intelligence?”.

• The Early Universe: This is just starting now with the James Webb Telescope peering into the dark depths of history–nearly to the Big Bang itself.

• Multiple Dimensions: String theory likes to live in 11-dimensional space, so what other parts of our physical universe live there too? Dark Matter? Dark Energy? Do all the extra dimensions need to be compact?

• The Arrow of Time: The physics of time is possibly the greatest unsolved problem in physics. Why does it only go one way?

• Singularity Physics: What happens at the center of a Black Hole? Do wormholes provide hyperspace bypasses? These questions may yet get answers from theoretical physics though likely not from the laboratory unless it is from an AMO analog.

References

[1] E. Knill, R. Laflamme and G. J. Milburn, A Scheme for Efficient Quantum Computation with Linear Optics, Nature 409 (6816), 46–52 (2001).

[2] D. NOLTE, A. LANGE and P. RICHARDS, Far-Infrared Dichroic Bandpass-Filters, Applied Optics 24 (10), 1541–1545 (1985).

[3] CERN. (2012, July 4). CERN experiments observe particle consistent with long-sought Higgs boson [Press release]. https://home.cern/news/press-release/cern/cern-experiments-observe-particle-consistent-long-sought-higgs-boson; ATLAS Collaboration. (2012). Observation of a new particle in the search for the Standard Model Higgs boson with the ATLAS detector at the LHC. Physics Letters B, 716(1), 1–29. https://doi.org/10.1016/j.physletb.2012.08.020 Cited by: 13000+; CMS Collaboration. (2012). Observation of a new boson at a mass of 125 GeV with the CMS experiment at the LHC. Physics Letters B, 716(1), 30–61. https://doi.org/10.1016/j.physletb.2012.08.021

Phase space of the Standard Map showing Hamiltonian Chaos with the first 5 Metallic Means
by David D. Nolte

The Golden Path to Chaos: Adiabatic Twists

If ever there was a magic number that encoded the mysteries of the universe, then surely it must be the golden mean. It seems to pop up everywhere. In flowers and hurricanes. In pine cones and sea shells. In architecture and infinite sums. In telescoping cascades of golden rectangles in the human figure.

Fig. 1. The golden mean can be found in numerous ratios of the measurements of the human body.

It also rears its head in the world of chaos theory, governing how a twisting dumbbell rotor transitions from regular motion to chaotic motion when it is tapped gently at a regular period.

The Golden Ratio

The Golden ratio can be defined in many ways, but its most common expression is given by

Among its many marvelous properties, one is that it is the hardest number to approximate with a ratio of small integers.  For instance, the ratio 89/55 is a number that is as close as one part in ten thousand to the golden mean but it is hardly a ratio of small integers.  This result may seem obscure, but there is a systematic way to find the ratios of integers that approximate an irrational number. This is known as continued fractions.

The continued fraction for the golden mean has an especially simple repeating form

also written as

This continued fraction has the slowest convergence for its continued fraction of any other number. Hence, the Golden Ratio can be considered, using this criterion, to be the most irrational number of all, and it governs the last straw of order as chaos emerges from a surprisingly simple map.

The Kicked Rigid Rotor

The rigid rotator (the simple dumbbell) is one of the iconic systems in physics. It is a classic object in the study of rotational dynamics, showing up in Lagrangian formulations as well as Euler’s equations. It is also a classic system in elementary quantum mechanics, illustrating the quantization of angular momentum. In the current setting (Hamiltonian chaos), it is an example of a periodically perturbed system that displays beautiful phenomena.

In chaos theory, the relationship between a continuous dynamical system and its discrete map is sometimes difficult to identify.  However, a discrete map arises naturally from a randomly kicked dumbbell rotator.  The system has an angular momentum J and a physical angle θ.  The strength of the angular momentum kick is given by the perturbation parameter ε, and the torque of the kick is a function of the physical angle θ.  The kicked rotator has the Hamiltonian

where the kicks are evenly timed with period T.  The perturbation parameter ε can be large.  The perturbation amplitude and sign depend on the instantaneous angle θ.  The equations of motion from Hamilton’s equations are

The values for J and θ just before the nth successive kick are Jn and qn, respectively.  Because the evaluation of the variables occurs at the period T, these discrete observations represent the values of a Poincaré section. 

The Chirikov Twist Map

The phase space (in action-angle coordinates) of the rigid rotator is particularly attractive for applications because it is simply a linear flow that has increasing velocities with increasing action J. In action-angle representation, it is a twist map, where circles outside the radius for J = 0 twist in one direction but inside that radius they twist in the opposite direction. David Birkhoff showed in 1913, while proving Poincaré’s last geometric theorem, that a simple periodic perturbation of this system creates a set of closed trajectories (around an elliptical point) and a set of open trajectories (around a hyperbolic point).

Fig. 2. The action-angle phase space of a rigid rotator, plus the associated twist map.

The rotator dynamics are continuous between each kick, leading to the discrete map (known as the Standard Map or the Chirikov Map)

in which the rotator is “strobed”, or observed, at regular periods of 2π. When ε = 0, the orbits on the (θ, J) plane are simply horizontal lines—the rotator spins with regular motion at a speed determined by J.

As the strength of the kick ε increases from zero, the Poicaré-Birkhoff theorem kicks in, and a first “island chain” appears with a single elliptical point paired with a single hyperbolic point. Then at larger values of ε new island chains appear, first with two islands, then with three, as in the figure below with ε = 0.3. Orbits that produce two islands are in a 2:1 resonance, and with three islands are in either a 3:1 or a 3:2 resonance. With increasing ε, more and more island chains open up, representing higher resonances.

Fig. 3 Chirikov map for ε = 0.3. The 1/1, 1/2 and 1/3 (2/3) island chains have opened with a primary hyperbolic point on the 1/1 resonance.

Each resonance is associated with a ratio of small integers: 1/2; 2/3; 3/4; 4/5 and beyond. These are the natural harmonics of the system. As the integers get larger, the ratios begin to approximate irrational numbers.

For instance, the number pi is approximated to increasing accuracy by the sequence of ratios:

Fig. Successive convergents of the irrational number pi.

These are called convergents and are obtained by taking more terms in the continued fraction representation of pi.

One of the fundamental findings of the theory of resonances in Hamiltonian systems is the decreasing “weight” of resonances associated with ratios of larger integers. Therefore, the 1:2 resonance is by far the most robust, the first to spring into existence, and it survives up to extremely strong perturbations. The 1:3 resonance is also relativety robust, but already the 1:4 and 1:5 resonances are more sensitive to perturbation and break up into island chains under moderate perturbation. Clearly the 22:7 ratio would not be sensitive nor the 333:106 resonance. These orbits would resist breaking up. Furthermore, once a resonance turns into an island chain, it creates hyperbolic points that can nucleate chaotic trajectories.

An example of the twist map at strong perturbation ε = 1.0 is shown in Fig. 4. There are numerous island chains. It is easy to find the 1:2 through the 1:7 resonances, but beyond that it is much more difficult to find these rational resonance. Furthermore, there are significant regions of chaotic trajectories associated with the hyperbolic points of the 1:2, 1:3, 1:4 and 1:5 resonances.

Fig. 4. The Standard map at ε = 1.0 slightly above the threshold for the dissolution of the Golde-Mean-Orbit.

In the midst of the island chains and the chaos, there are still continuous (open) orbits that span the phase space without breaks. These are the most irrational numbers–numbers like the golden mean. These are the last orbits to break up. The critical threshold for the breakup of the golden-mean orbit is ε = 0.971. The plot in Fig. 4 is just above that threshold.

All of this behavior of the Standard Map follows from KAM theory, developed by Kolmogorov, Arnold and Moser in the early 1960’s. Although the standard map is specific to the tapped spinning disk, the results and behavior are very general for a wide class of two-dimensional Hamiltonian dynamical systems.

Adiabatic Following: Orbits of the Noble Means

The golden mean is not the only “slowest convergent” among irrational numbers. There are an entire class of irrational numbers whose continued fractions terminate with an infinite series of “1”s. These are known as the “Noble Means”. Examples are:

where the sequence, as q increases to infinity, converges on unity asymptotically among the set of irrationals with the slowest convergents.

There are also the so-called “Metallic Means”, beginning with Gold and moving to Silver, Bronze, Copper, and Nickel. These are:

The challenge for numerical simulations is to find the orbits associated with these Metallic Means for large perturbation parameters ε. One cannot simply pick an initial condition for the Standard Map equal to a Metallic Mean, because at large perturbation, all the orbits have already shifted from their zero-perturbation values.

One of the most important principles in classical mechanics is the concept of adiabatic invariance. All the most common conservation laws of introductory physics–conservation of energy, momentum, and angular momentum–are consequences of adiabatic invariance. Indeed, the phase space of the rigid rotator is ideal for tracking adiabatic invariance because the J-value is the adiabatic invariant. In the numerical simulation, one begins with ε = 0, chooses an initial condition J = φn, and iterates the map as ε slowly increases.

This is shown in the following YouTube video. You will see five special orbits evolve as the perturbation is slowly increased. These are M1 (red), M2 (blue), M3 (green) and two resonances 3:1 (cyan) and 4:1 (magenta). The resonances are expected to break into island chains at relativity low perturbation ε, which is confirmed in the video.

Fig. 5 YouTube video of the Standard Map and special orbits as the perturbation slowly (adiabatically) increases.

Interestingly, the silver mean breaks into a 5:1 island chain around the same perturbation level. This is because the Silver Mean equals 0.414 which approaches 8/5 at moderate perturbation. Therefore, the Silver Mean orbit is “captured” by a 1:5 resonance and remains stable up to very large perturbations approaching ε = 1. The Bronze Mean is captured relativity early into the 1:1 resonance island.

References:

Music: The Beat Lessons (Band Camp): Link

D. D. Nolte, Introduction to Modern Dynamics, 2nd ed. (Oxford University Press, 2019) Link

This Post is Based on Simulations from Chapter 5 of IMD, 2nd edition

This Blog Post is a Companion to the undergraduate physics textbook Modern Dynamics: Chaos, Networks, Space and Time, 2nd ed. (Oxford, 2019) introducing Lagrangians and Hamiltonians, chaos theory, complex systems, synchronization, neural networks, econophysics and Special and General Relativity to Junior and Senior physics majors.

Schrodinger's Cat
by David D. Nolte

How Fat is Schrödinger’s Cat?

There is more than one absurdity hidden behind the gauzy clouds of quantum physics.  No matter how hard the Ecclesiastes of the quantum canon have tried to hide them, the absurdities always tended to shine through.  Niels Bohr, the high priest of the quantum, established the dogma in the raiment of the Copenhagen interpretation that became a windmill tilted at by the Don Quixote’s of physics.  Surprisingly, two of the first to tilt at Copenhagen were also two of the founders of the field: Einstein and Schrödinger. Schrödinger created an absurdity—his “Cat”—that he thought would slay Bohr’s windmill, only to see it embraced by the enemy in its tiniest form, and then to grow ever larger until today some of the cat’s descendants are so fat they can be seen with the naked eye.

Einstein’s Spooky Action and Schrödinger’s Cat

Albert Einstein and Erwin Schrödinger were founders of quantum physics.  Einstein, on his part, blew past Planck by embracing quanta in the form of the quantum of light—the photon.  Schrödinger, just as important, found the wave equation that governed the behavior of quantum particles.  These two physicists believed that quantum dynamics should be just as deterministic as classical dynamics, and they pushed hard against Max Born and Niels Bohr and Werner Heisenberg who embraced the fundamental uncertainties of quantum measurement.

In the view of Einstein and Schrödinger, beginning in 1925, quantum mechanics had slowly veered off the tracks, and by 1935 they felt it had coagulated into a form that was both unrecognizable and unpalatable. 

Einstein took the first pass, tilting at the nonlocal character of quantum physics that allowed a measurement at one location to determine the measurement at a distant location, no matter how far apart the two locations were.  This is the famous “EPR Paradox”, named after the three authors of the paper published in the Physical Review in 1935 by Einstein, Podolsky and Rosen.  Einstein called it “Spooky action at a distance.” 

After reading the EPR paper, Schrödinger sent a congratulatory note to Einstein, applauding him on his clever thought experiment that showed one of the absurdities of quantum physics.  This note launched an intense correspondence between the two physicists, as each complained to the other about the overbearing Copenhagen interpretation and about the indifference of a ballooning number of physicists who were happy to adopt Bohr’s attitudes without worrying about the underlying philosophical contradictions.

1927 Solvay Congress with Einstein, Compton and Schrödinger.
Fig. 1 Schrödinger (top) and Einstein (bottom) at the 1927 Solvay Congress.

Inspired by his correspondence with Einstein, Schrödinger launched his own attack on Copenhagen.  Where Einstein attacked the nonlocality of quantum phenomena, Schrödinger attacked the scale of quantum phenomena.

Schrödinger’s Cat

In late 1935, Schrödinger published a series of papers discussing the current situation in quantum mechanics [1].  Schrödinger had remained a realist.  Although Born had established almost ten years before that the quantum wavefunction was not related to the physically real electron density, Schrödinger continued to ascribe to it a level of physical reality.  To reduce the Copenhagen interpretation to absurdity, he took Bohr’s measurement argument to extremes.

Schrödinger proposed placing a cat in a sealed box with a radioactive substance known to have a half-life of an hour.  If the particle decays, a Geiger counter in the box releases a hammer that smashes a vial of poison, killing the cat.  At the end of an hour, the chance the cat is alive or dead is 50/50.  In the Copenhagen interpretation, because all elements in the box consist of quantum mechanical wavefunctions, and no overt measurement is made, the cat must be in a quantum superposition of both alive and dead states.  Now if an observer opens the box to look inside, the wavefunction of the cat collapses into one state or the other.  To Schrödinger, such a state of affairs was absurd, clearly illustrating the limitations of the Copenhagen interpretation that required wavefunction superpositions to remain unmolested if no overt measurement takes place.

Schrödinger's Cat introduced in Naturwissenschaften 1935
Fig. 2 Schrödinger’s introduction of his cat in the Nov. 29 issue of Naturwissenschaften of 1935 in the article “The Current Situation of Quantum Mechanics”.

The translation of Schrödinger’s introduction of his cat (Fig. 2) is:

“One can even construct quite burlesque cases. A cat is penned up in a steel chamber, along with the following hellish machine (which must be secured against direct interference by the cat): in a Geiger counter, there is a tiny amount of radioactive substance, so little that in the course of an hour, perhaps one of the atoms decays, but also, with equal probability, perhaps none; if it happens, the counter tube responds and discharges through a relay a little hammer that shatters a small flask of prussic acid [hydrogen cyanide].

If one has left this entire system to itself for an hour, one would say that the cat still lives if no atom has decayed in the meantime. The first atomic decay would have poisoned it. The ψ-function of the entire system would express this by having in it the living and the dead cat (if I may be forgiven the expression) mixed or smeared out in equal parts.

The typical thing about these cases is that an uncertainty originally restricted to the atomic domain becomes transformed into macroscopic uncertainty, which can then be resolved by direct observation. This prevents us from so naively accepting a ‘blurred model’ as a representation of reality. In itself, it would contain nothing unclear or contradictory. There is a difference between a shaky or out-of-focus photograph and a snapshot of clouds and fog banks.”

The Schrödinger cat paradox became sensationally famous in ways that Schrödinger himself had not intended.  He had fashioned the example to combat what he saw was an unrealistic acceptance of the Copenhagen interpretation of quantum mechanics. While succeeding in showing that quantum mechanics was bizarre, he had hoped to show that it was wrong, or at least missing something.  To his chagrin, there was general acceptance of the dead-and-alive superposition, at least in principle.  Schrödinger had called the mutual influence of quantum states upon each other as entanglement, and the word stuck.  The discussions elicited by the cat paradox side-stepped the philosophical problems of quantum mechanics and focused instead on the physical differences between microscopic states, where quantum superposition held sway, versus macroscopic states, where classical physics emerges.

Today, the quantum/classical border is understood to be governed by decoherence. When a quantum system (with its well-defined superpositions) interacts with its environment, the internal quantum states become entangled with the environmental states, and the internal states lose their originally clean relationships, becoming fuzzy—less both “dead and alive” to become more “dead or alive”. By the simple combinatorics of large numbers, the bigger a quantum state is, the more avenues there are to interact with its environment, and the faster the effects of decoherence kick in. The question then shifts from whether a quantum cat can exist, to how large the quantum cat can become before decoherence gets too fast to capture the superposition.

Schrödinger’s Cat Grows Up

For the first several decades of its life, the size of Schrödinger’s cat was restricted to the quantum physics of fundamental particles, like electrons, or to electronic superpositions within atoms or molecules. These superpositions were not “spatial”—the two entities of the superposition were not occupying different parts of space. The electronic states of atoms could be in different orbitals that have different spatial distributions, but it is all one object.

This changed in 1974 when Italian physicists Pier Giorgio Merli, Gian Franco Missiroli, and Giulio Pozzi at the University of Bologna used the electron source of an electron microscope to send single electrons, one at a time, through a biprism acting as a double slit (like Young’s double slit experiment with light). This was the first time that the electron double-slit experiment was performed one electron at a time, and despite the fact that there was no “other” electron to interfer with, the experiment produced interference fringes. Each electron was in a superposition, taking both one path and the other, separated spatially by the two halves of the biprism. This was the first demonstration of Schrödinger’s cat as a spatial superposition.

This experiment was followed 15 years later by researchers at Hitachi in Japan who, in 1989, used a scintillator screen to watch the single electrons arrive one at a time, slowly building up the interference fringes first seen by the Italians.

Fig. 3 Promotional video by Hitachi showing the accumulating electrons, forming interference fringes.

Electrons interfering with themselves, by taking different spatial paths, still represents a tiny cat. Of the stable fundamental particles, electrons are the lightest (or the “smallest”). A more impressive cat might be constructed of an atom that is heavier and “larger” than an electron.

In 1996, Chris Monroe and David Wineland at JILA created a Schrödinger Cat superposition using a trapped Beryllium ion [2]. They coupled the internal electronic states to external motional states that allowed the ion to be prepared in a superposition of spatially separated states.

Fig. 4 The Monroe and Wineland experiment. Published May 24, 1996 issue of Science.

An even larger cat was demonstrated in 1999 by Anton Zeilinger‘s group in Vienna by creating a spatial quantum superposition using “Buckyballs” [3] that are C60 molecules. They used a thermal molecular beam at low flux levels that ensured that the average number of molecules transiting the experimental apparatus at a given time was less than one. One member of the group, Markus Arndt, has been “scaling up” the size of his cats into the range of thousands of atoms.

Fig. 5 The Carbon-60 paper from Zeilinger’s group in Nature, Oct 14, 1999

Schrödinger’s Cat Today

In the last 10 years, Schrödinger’s cat has grown to immense size. In 2023 a group at ETH in Zurick, Switzerland, put a “Fat Cat” 16-microgram mass [4] into a spatial superposition of two states of mechanical vibration. The mass contained approximately 1017 atoms (C60 has 60 atoms), which clearly brought quantum mechanics to the edge of the macroscopic world. It was shaped as a disc with a diameter of about 1 millimeter and a thickness of of 100 microns, large enough to be seen with the naked eye (before it is loaded into the ultra-low-temperature cryostat where it is hidden from probing eyes). The states experienced decoherence after about 40 microseconds, but this is a sufficiently long time for experimental probes to test its properties.

Fig. 6 The “Fat Cat” of the April 21 issue of Science from 2023.

The 16-microgram mass experiment was macroscopic but still comprised a single object in two spatial modes. Therefore, by building on the C60 experiment of Markus Arndt, in early 2026 a matter wave interferometer measured the interference of large metal clusters of sodium [5] containing approximately 7000 atoms passing through a region of space that was macroscopically large relative to the size of the metal clusters. By some measure of “macroscopicity” this is the largest Quantum Cat to date.

Largest Schrödinger's Cat
Fig. 7 The “Fatest Cat” of Jan. 21 issue of Nature (2026)

A simplified schematic of the Pedalino experiment is shown in Fig. 8. A nanoclusters with about 7000 sodium atoms comes from a source and moves towards a standing-wave laser beam. If the cluster moves into an antinode, then it is ionized and removed, but if it enters a node region, it remains neutral and passes through. This creates a spatial superposition of “locations” of the nanoparticle. This superposition creates quantum interference fringes on the far side of the diffraction grating.

Metal nanoparticle interferometer
Fig. 8. Simplified view of the Pedalino experiment. A sodium nanocluster with about 7000 sodium atoms is sent through a standing-wave optical field that acts as a diffraction grating. The nanoparticle passes through any of the anti-nodes of the standing wave in a spatial superposition that causes interference fringes on the far side. At one instance of time, the nanoparticle is both here and there, “dead” and “alive”.

The nanoparticle is about 10 nm in size, which is comparable to some biological macromolecules as well as viruses, raising the possibility that quantum cats may be constructed in the near future of biological matter. It may even become possible to produce quantum cats from living bacteria. Experimental groups continue to push the bounds of large quantum systems. This is of more than “academic” interest, because larger quantum superpositions with longer decoherence times can be enlisted as elements of quantum information systems such as quantum computers and quantum communication systems.

References

[1] Schrodinger, E. (1935). “The current situation in quantum mechanics.” Naturwissenschaften 23: 807-812.

[2] P.G. Merli, G.F. Missiroli, and G. Pozzi, “Electron interferometry with the Elmiskop 101 electron microscope,” Journal of Physics E: Scientific Instruments 7 (1974), 729–732

[3] C. Monroe et al. , A “Schrödinger Cat” Superposition State of an Atom. Science272,1131-1136(1996). DOI:10.1126/science.272.5265.1131

[4] Arndt, M., Nairz, O., Vos-Andreae, J. et al. Wave–particle duality of C60 molecules. Nature 401, 680–682 (1999). https://doi.org/10.1038/44348

[5] Marius Bild et al., Schrödinger cat states of a 16-microgram mechanical oscillator. Science380, 274-278(2023). DOI:10.1126/science.adf7553

[5] Pedalino, S., Ramírez-Galindo, B.E., Ferstl, R. et al. Probing quantum mechanics with nanoparticle matter-wave interferometry. Nature 649, 866–870 (2026). https://doi.org/10.1038/s41586-025-09917-9

The Rise of Wave Mechanics by Erwin Schrödinger
by David D. Nolte

100 Years of Quantum Physics: Schrödinger’s Wave Mechanics (1926)

By the middle of 1925, a middle-aged Erwin Schrödinger was casting about, bogged down in mid career, looking for something significant to say about the rapidly accelerating field of quantum theory.  He was known for his breadth of knowledge, and for his belief in his own creative genius [1], but a grand synthesis had so far eluded him. 

Einsteinian Gas Theory

In the middle of the year, Schrödinger was deep analyzing two papers recently published by Einstein (Sept. 1924 and Feb. 1925) on the quantum properties of ideal gases where Einstein applied the new statistical theory of Bose to the counting of states in a volume of the gas [2].  One of the intriguing discoveries made by Einstein in those papers was a close analogy between the fluctuation of gas numbers and the interference of waves.  He stated:

‘I believe that this is more than a mere analogy; de Broglie has shown in a very important work how a (scalar) wave field can be coordinated with a material particle or a system of material particles’

referring to de Broglie’s thesis work of 1924 that associated a wave-like property to mass.  Einstein had been the first to attribute a wave-particle duality to the quantum phenomenon of black-body radiation, giving a lecture in Salzburg, Austria, in 1909 showing relationships between the particle-like and the wave-like properties of the radiation, and he found similar behavior in the properties of monatomic ideal gases, though his derivations were purely statistical.

Erwin Schrödinger photo
Fig. 1 Erwin Schrödinger (Source)

Schrödinger was suspicious of the “unnatural” way of counting states used by Einstein and Bose for the gas, and he sought a more “natural” way of explaining how the elements of phase space were filled.  It struck him that, just as Planck’s black-body radiation spectrum could be derived by assuming discrete standing-wave modes for the electromagnetic radiation, then perhaps the behavior of ideal gases could be obtained using a similar approach.  He and Einstein exchanged several letters about this idea as Schrödinger dug deeper into de Broglie’s theory.

The Zurich Seminar

At that time, Schrödinger was in the Chair of Theoretical Physics at the University of Zurich, holding the same chair that Einstein had held 15 years earlier.  Following Einstein, the chair had been occupied by Max von Laue and then by Peter Debye who moved to the ETH in Zurich.  Debye organized a joint seminar between the University and ETH that was a hot social gathering of physicists and physical chemists, discussing the latest developments in atomic and quantum science. 

In November of 2025, Debye, who probably knew about the Einstein-Schrödinger discussion on de Broglie, asked Schrödinger to give a seminar on de Broglie’s theory to the group.  A young Felix Bloch, who was a graduate student at that time, recalled hearing Debye say something like

“Schrödinger, you are not working right now on very important problems anyway. Why don’t you tell us sometime about that thesis of de Broglie, which seems to have attracted some attention?”[3]

Schrödinger gave the overview seminar in early December, showing how the Bohr-Sommerfeld quantization conditions could be explained as standing waves using de Broglie’s theory, but Bloch recalled Debye was unimpressed, saying that de Broglie’s way of talking was “childish” and that what was needed for a proper physics theory was a wave equation.

This exchange between Schrödinger and Debye was recalled only in later years, and there is debate about what exactly was said and what effect it had on Schrödinger.  From Schrödinger’s letters to friends, it is clear that he was already well into his investigations of wavelike properties of matter when Debye asked him to give the seminar.  Furthermore, he had already tried to construct wave packets using superpositions of phase waves propagating along Bohr-Sommerfeld elliptical orbits but had been led to ugly caustics when he tried to apply the packets to the hydrogen atom [4].  Therefore, although Debye was probably not the source of Schrödinger’s interest in de Broglie, it is possible that Debye’s quip about “childishness” may have spurred Schrödinger to find a wave equation subject to boundary conditions rather than working with packets following ray paths.

The Christmas Breakthrough

By this time, Christmas was approaching and Schrödinger arranged to take a vacation away from his family to the Swiss Alpine village of Arosa, and given his unconventional belief in the link between personal pleasure and genius, he did not go alone.  There is no record of what transpired, and no record of which mistress was with him on this particular trip, nor how she spent her time while he worked on his theory, but two days after Christmas he wrote a letter to the physicist Willy Wien saying

“At the moment I am struggling with a new atomic theory. If only I knew more mathematics! I am very optimistic about this thing, and expect that, if only I can . . . solve it, it will be very beautiful.. . . I hope that I can soon report in a little more detailed and understandable way about the matter. At present I must learn a little mathematics in order to completely solve the vibration problem …”[5]

He had uncovered his first wave equation.  When he returned to Zurich, he enlisted the help of his friend, the mathematician Hermann Weyl at the University in Zurich, and Schrödinger had his first eigenfrequencies for hydrogen.  But they were wrong!

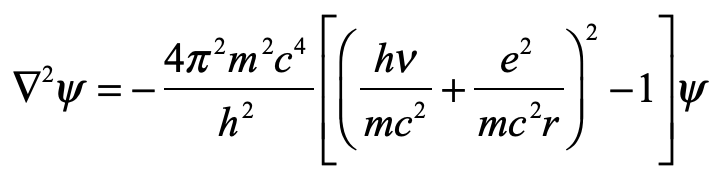
Fig. 2 Schrödinger’s first wave equation was relativistic.

The theory of de Broglie was fundamentally a relativistic theory, motivated by mapping the behavior of matter onto the behavior of light.  Therefore, Schrödinger’s first attempt was also relativistic, equivalent to the Klein-Gordon equation.  But there was no clear understanding of electron spin at that time, even though it had been established as a fundamental property of the electron.  It was only several years later when Dirac correctly accounted for electron spin in a relativistic wave equation. 

Dirac relativistic quantum wave equation
Fig. 3 The full relativistic Dirac equation.

The Schrödinger Wave Equation

Convinced that he was onto something big, and unwilling to fail, despite his failure to obtain correct values for hydrogen, Schrödinger went back to first principles, to the classical theory of Hamiltonian mechanics, identifying Hamilton’s characteristic function with the phase of an electron wave and deriving a non-relativistic equation using variational principles subject to boundary conditions.  The eigenvalues of this new equation, when applied to hydrogen, matched the Bohr spectrum perfectly!

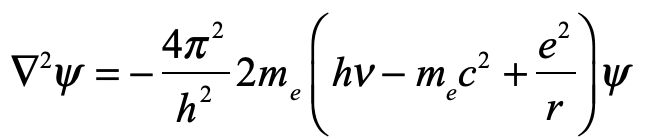
Fig. 4. Schrödinger’s second wave equation was non-relativistic and correctly matched the Bohr energy levels of hydrogen.

It had been only a few weeks since Schrödinger had given his previous seminar to the Zurich group, but in January he gave his update, probably given with some degree of satisfaction, having Debye in attendance, showing his now-famous wave equation and the agreement with experiment.  Schrödinger wrote up his theory and results and submitted his paper on January 27, 1926, to Annalen der Physik [6].

Hydrogen quantum orbitals
Fig. 5 Hydrogen quantum orbitals (Source)

Schrödinger had been known, but not as a forefront thinker, despite what he believed about himself.  Now he was a forefront thinker, vindicating his beliefs but not always on the right track.  He continued his unconventional lifestyle, marginalizing him socially, and he resisted Max Born’s and Niels Bohr’s probabilistic interpretations of the meaning of his own quantum wavefunction, marginalizing him professionally.  Yet his breakthrough gave him a platform, and his skeptical reactions to his colleague’s successes helped illuminate the nature of the new physics (“Schrödinger’s Cat” [7]) through the decades to follow.

Bibliography

A very large body of historical work exists on the discovery of the Schrödinger equation, partially fueled by the lack of first-person accounts on how he achieved it.  There has been a lot of speculation and a lot of sleuthing to uncover his path of discovery. Several accounts differ mainly in the timing of when he derived his equations, although all agree on the sequence: that the relativistic equation preceded the non-relativistic one. Here is a small sampling of the literature:

• Hanle, P. A. (1977). “The Coming of Age of Erwin Schrödinger: His Quantum Statistics of Ideal Gases.” Archive for History of Exact Sciences, 17(2), 165–192. DOI: 10.1007/BF00328532.

• Hanle, P. A. (1979). “The Schrödinger‐Einstein correspondence and the sources of wave mechanics.” American Journal of Physics, 47(7), 644–648. DOI: 10.1119/1.11587.

• Mehra, Jagdish. “Erwin Schrödinger and the Rise of Wave Mechanics. II. The Creation of Wave Mechanics.” Foundations of Physics, vol. 17, no. 12, 1987, pp. 1141-1188.

• Renn, J. (2013). “Schrödinger and the Genesis of Wave Mechanics.” In W. L. Reiter & J. Yngvason (Eds.), Erwin Schrödinger – 50 Years After (pp. 9–36). Zurich: European Mathematical Society. DOI: 10.4171/121-1/2.

• Wessels, L. (1979). “Schrödinger’s Route to Wave Mechanics.” Studies in History and Philosophy of Science Part A, 10(4), 311–340.

Notes

[1] He led an unconventional lifestyle (some would say emotionally predatory) based on his belief in the personal origins of genius.  Although this behavior presented significant social barriers to his career, he refused to abandon it.

[2] A. Enstein, ‘Quantentheorie des einatomigen idealen Gases’, Preuss. Ak. Wiss. Sitzb. (1924) pp. 261 – 267, and (1925), pp. 3-14.

[3] Quoted in Mehra, pg. 1150

[4] Mehra, pg. 1147

[5] Wessels, pg. 328

[6] Schrödinger, Erwin. “Quantisierung als Eigenwertproblem (Erste Mitteilung).” Annalen Der Physik, vol. 384, no. 4, 1926, pp. 361-376.

[7] Schrödinger, E. (1935). “Die gegenwärtige Situation in der Quantenmechanik.” Naturwissenschaften 23: 807–812, 823–828, 844–849.  Schrödinger, E. (1980). “The Present Situation in Quantum Mechanics: A Translation of Schrödinger’s ‘Cat Paradox’ Paper.” Proceedings of the American Philosophical Society 124 (5): 323–338. (Translated by J. D. Trimmer).

Books by David Nolte at Oxford University Press
Read more in Books by David Nolte at Oxford University Press

by David D. Nolte

100 Years of Quantum Physics: Rise of the Matrix (1925)

Niels Bohr’s atom, by late 1925, was a series of kludges cobbled together into a Rube Goldberg type of construction.  On the one hand, there was the Bohr-Sommerfeld quantization conditions that let Bohr’s originally circular orbits morph into ellipses like planets in the solar system.  On the other hand, there was Pauli’s exclusion principle that partially explained the building up of electron orbits in many-electron atoms, but to many it seemed like an ad hoc rule. 

The time was ripe for a new perspective. Enter the wunderkind, Werner Heisenberg.

Heisenberg’s Trajectory

Werner Heisenberg (1901 – 1976) was the golden boy—smart, dashing, ambitious. He excelled at everything he did and was a natural leader among his group of young friends. He entered the University of Munich in 1920 at the age of 19 to begin working towards his doctorate degree in mathematics, but he quickly became entranced with an advanced seminar course given by Arnold Sommerfeld (1868 – 1951) on quantum mechanics. His studies under Sommerfeld advanced quickly, and he was proficient enough to be “lent out” to the group of Max Born and David Hilbert at the University of Göttingen for the 1922-1923 semester when Sommerfeld was on sabbatical at the University of Wisconsin, Madison, in the United States. Born was impressed with the young student and promised him a post-doc position upon his graduation with a doctoral degree in theoretical physics the next year (when Heisenberg would be just 22 years old).

Unfortunately, his brilliantly ascending career ran headlong into “Willy” Wien who had won the Nobel Prize in 1911 for his displacement law of black body radiation. Wien was a hard-baked experimentalist who had little patience with the speculative flights of theoretical physics. Heisenberg, in contrast, had little patience with the mundane details of experimental science. The two were heading for an impasse.

The collision came during the oral examination for Heisenberg’s doctoral degree. Wien, determined to put Heisenberg in his place, opened with a difficult question about experimental methods. Heisenberg could not answer, so Wien asked a slightly less difficult but still detailed question that Heisenberg also could not answer. The examination went on like this until finally Wien asked Heisenberg to derive the resolving power of a simple microscope. Heisenberg was so flustered by this time that he could not do even that. Wien, in disgust, turned to Sommerfeld and pronounced a failing grade for Heisenberg. After Heisenberg stepped out of the room, the professors wrangled over the single committee grade that would need to be recorded. Sommerfeld’s top grade for Heisenberg’s mathematical performance and Wien’s bottom grade for his experimental performance led to the compromise grade of a “C” for the exam—the minimum grade sufficient to pass.

Heisenberg was mortified. Accustomed always to excelling and being lauded for his talents, Heisenberg left town that night, taking the late train to Göttingen where a surprised Born found him outside his office early the next morning—fully two months ahead of schedule. Heisenberg told him everything and asked if Born would still have him. After learning more about Wien’s “ambush”, Born assured Heisenberg that he still had a place for him.

Heisenberg was so successful at Göttingen, that when Born planned to spend a year sabbatical at MIT in the United States for the 1924-1925 semester, Heisenberg was “lent out” to Niels Bohr in Copenhagen. While there, Heisenberg, Bohr, Pauli and Kramers had intense discussions about the impending crisis in quantum theory. Bohr was fully aware of the precarious patches that made up the quantum theory of the many-electron atom, and the four physicists attempted to patch it yet again with a theoretical effort led by Kramers to try to reconcile optical transitions in the atomic spectra. But no one was satisfied, and the theory had serious internal inconsistencies, not the least of which was a need to sacrifice the sacrosanct principle of conservation of energy.

Through it all, Heisenberg was thrilled by his deep involvement in the most fundamental questions of physics of the day and was even more thrilled by his interactions with the great minds he found in Copenhagen. When he returned to Göttingen on April 27, 1925, the arguments and inconsistencies were ringing in his head, infecting the group at Göttingen with the challenging physics, especially Max Born and Pascual Jordan.

Little headway could be made, until Heisenberg had a serious attack of hay fever that sent him for respite on June 7 to the remote island of Helgoland in the North Sea far off of the coast from Bremerhaven. The trip cleared Heisenberg’s head—literally and figuratively—as he had time to come to grips with the core difficulties of quantum theory.

Trajectory’s End

The Mythology of Physics recounts the tale of when Heisenberg had his epiphany, watching from the beach as the sun rose over the sea. The repeated retelling has solidified the moment into revealed “truth”, but the origins are probably more prosaic. Strip a problem bare of all its superficial coverings and what remains must be the minimal set of what can be known. Yet to do so requires courage, for much of the superficial coverings are established dogma, embedded so deeply in the thought of the day that angry reactions must be expected.

Map of Heligoland, Germany
Fig. 1 Heligoland Germany. (From Google Maps and Wikipedia)

At some moment, Heisenberg realized that the superficial covering of atomic theory was the slavish devotion to the electron trajectory—to the Bohr-Sommerfeld electron orbits. Ever since Kepler, the mental image of masses in orbit around their force center had dominated physical theory. Quantum theory likewise was obsessed with images of trajectories—it persists to this day in the universal logo of atomic energy. Heisenberg now rejected this image as unknowable and hence not relevant for a successful theory. But if electron orbits were out, what was the minimal set of what can be known to be true? Heisenberg decided that it was simply the wavelengths and intensities of light absorbed and emitted by atoms. But what then? How do you create a theory constructed on transition energies and intensities alone? The epiphany was the answer—construct a dynamics by which the quantum system proceeds step-by-step, transition-by-transition, while retaining the sacrosanct energy conservation that had been discarded by Kramer’s unsuccessful theory.

The result, after returning to Göttingen, is Heisenberg’s paper, submitted July 29, 1925 to Zeitschrift für Physik titled Über quantentheoretische Umdeutung kinematischer und mechanischer Beziehungen (Over the quantum theoretical meaning of kinematic and mechanical relationships).

Heisenberg 1925 Over quantum theoretical meaning of kinematic and mechanical relationships
Fig. 2 The heading of Heisenberg’s 1925 Zeitschrift für Physik article. The abstract reads: “This work seeks to find fundamental principles for a quantum theoretical mechanics that is based exclusively on relationships among principal observable magnitudes.” [1]

Heisenberg begins with the fundamental energy relationship between the frequency of light and the energy difference in a transition

Heisenberg 1925 Zeitschrift fur Physik paper on transition energies
Fig. 3 Dynamics emerges from the transitions among different energy states in the atom [1].

His goal is to remove the electron orbit from the theory, yet positions cannot be removed entirely, so he takes the step of transforming position into a superposition of amplitudes with frequencies related to the optical transitions.

Heisenberg replacing the electron orbits with their Fourier coefficients based on transition frequencies.
Fig. 4 Replace the electron orbits with their Fourier coefficients based on transition frequencies [1].

Armed with the amplitude coefficients and the transition frequencies, he constructs sums of transitions that proceed step by step between initial and final states.

Heisenberg connecting initial and final states with series of steps that conserve energy.
Fig. 5 Consider all the possible paths between initial and final states that obey energy conservation [1].

After introducing the electric field, Heisenberg calculates the polarizability of the atom, the induced moment, using Kramer’s dispersion formula combined with his new superposition.

Heisenberg transition amplitude based on sums over possible energy steps
Fig. 6 Transition amplitude between initial and final states based on a series of energy-conserving transition steps [1].

Heisenberg applied his new theoretical approach to one-dimensional quantum systems, using as an explicit example the anharmonic oscillator, and it worked! Heisenberg had invented a new theoretical approach to quantum physics that relied only on transition frequencies and amplitudes—only what could be measured without any need to speculate on what types of motions electrons might be executing. Heisenberg published his new theory on his own, as sole author befitting his individual breakthrough. Yet it was done under the guidance of his supervisor Max Born, who recognized something within Heisenberg’s mathematics.

The Matrix

Heisenberg’s derivations involved numerous summations as amplitudes multiplied amplitudes in complicated sequences. The mathematical steps themselves were straightforward—just products and sums—but the numbers of permutations were daunting, and their sequential order mattered, requiring skill and care not to miss terms or to get minus signs wrong.

Yet Born recognized within Heisenberg’s mathematics the operations of matrix multiplication. The different permutations with sums of alternating signs were exactly what one obtained by taking determinants of matrices, and it was well known that the order of matrix multiplication mattered, where a*b ≠ b*a. With his assistant Pacual Jordan, the two reworked Heisenberg’s paper in the mathematical language of matrices, submitting their “mirror” paper to Zeitschrift on Sept. 27, 1925. Their title was prophetic: Towards Quantum Mechanics. This was the first time that the phrase “quantum mechanics” was used to encompass all of the widely varying aspects of quantum systems.

Born and Jordan 1925 Zur Quantenmechanik
Fig. 7 The header for Born and Jordan’s reworking of Heisenberg’s paper into matrix mathematics [2].

In the abstract, they state:

The approaches recently put forward by Heisenberg (initially for systems with one degree of freedom) are developed into a systematic theory of quantum mechanics. The mathematical tool is matrix calculus. After this is briefly outlined, the mechanical equations of motion are derived from a variational principle, and the proof is carried out that, on the basis of Heisenberg’s quantum condition, the energy theorem and Bohr’s frequency condition follow from the mechanical equations.  Using the example of the anharmonic oscillator, the question of the uniqueness of the solution and the significance of the phases in the partial oscillations are discussed.  The conclusion describes an attempt to incorporate the laws of the electromagnetic field into the new theory.

Born and Jordan begin by creating a matrix form for the Hamiltonian subject to Hamilton’s dynamical equations

Born Hamiltonian and Hamilton's equations
Fig. 8 Defining the Hamiltonian with matrix operators [2].

Armed with matrix quantities for position and momentum, Born and Jordan construct the commutator of p with q to arrive at one of the most fundamental quantum relationships: the non-zero difference in the permuted products related to Planck’s constant. This commutation relationship would become the foundation for many quantum theories to come.

Born 1925 matrix commutator
Fig. 9 Page 871 of Born and Jordan’s 1925 Zeitschrift article that introduces the commutation relationship between p and q [2].

As Heisenberg had done in his paper, Born and Jordan introduce the electric field of light to derive the dispersion of an atomic gas.

Max Born quantum transition amplitude from matrix elements
Fig. 10 Expression for the dispersion of light in an atomic gas [2].

The Born and Jordan paper appeared in the November issue of Zeitschrift für Physik, although a pre-print was picked up in England by Paul Dirac, who was working towards his doctoral degree under the mentorship of Ralph Fowler (1889 – 1944) at Cambridge. Dirac was deeply knowledgable in classical mechanics, and he recognized as soon as he saw it that the new quantum commutator was intimately connected to a quantity in classical mechanics known as a Poisson bracket. The Poisson bracket is part of Hamiltonian mechanics that defines how two variables, known as conjugate variables, are connected. For instance, the Poisson bracket of x with px is non-zero, meaning that these are conjugate variables, while the Poisson bracket of x with py is zero, meaning that these variables are fully independent. Conjugate variables are not “dependent” in an algebraic sense, but are linked through the structure of Hamilton’s equations—they are the “p’s and q’s” of phase space.

Dirac 1926 Proceedings of the Royal Society comparison of Poisson bracket to quantum commutator.
Fig. 11 The Poisson bracket in Dirac’s paper submitted on Nov. 7, 1925 [3].

Dirac submitted a paper on Nov. 7, 1925 to the Proceedings of the Royal Society of London where he showed that the Heisenberg commutator (a quantum quantity) directly proportional to the Poisson bracket (the classical quantity) with a proportionality factor that depended on Planck’s constant.

Dirac quantum commutation relationship
Fig. 12 Dirac relating the quantum commutator to the classical Poisson (Jacobi) bracket [3].

The Drei-Männer Quantum Mechanics Paper: Born, Heisenberg, and Jordan

Meanwhile, back in Göttingen, the three quantum physicists Born, Heisenberg and Jordan now combined forces to write a third foundational paper that established the full range of the new matrix mechanics. Heisenberg’s first paper had been the insight. Born and Jordan’s following paper had re-expressed Heistenberg’s formulas into matrix algebra. But both papers had used simple one-dimensional problems as test examples. Working together, they extended the new quantum mechanics to systems with many degrees of freedom.

Quantum Mechanics. Born, Heisenberg and Jordan three-man paper heading.
Fig. 13 Header for the completed new theory on quantum mechanics by Born, Heisenberg and Jordan [4].

With this paper, the matrix properties of dynamical variables are defined and used in their full form.

Quantum Mechanics. Born, Heisenberg and Jordan. View of a matrix.
Fig. 14 An explicit form for a dynamical matrix in the “three-man” paper [4].

With the theory out in the open, Pauli in Hamburg and Dirac at Cambridge used the new quantum mechanics to derive the transition energies of hydrogen, while Lucy Mensing and J. Robert Oppenheimer in Göttingen extended it to the spectra of more complicated molecules.

Open Issues

Heisenberg’s matrix mechanics might have exclusively taken hold of the quantum theory community and we would all be using matrices today to perform all our calculations. But within one month of the success of matrix mechanics, an alternative quantum theory would be proposed by Erwin Schrödinger based on waves, a theory that came to be called wave mechanics. There was a minor battle fought over matrix mechanics versus wave mechanics, but in the end, Bohr compromised with his complementarity principle, allowing each to stand as equivalent viewpoints of quantum phenomena (but more about Schrödinger and his waves in my next Blog).

Further Reading

For more stories about the early days of quantum physics read Chapter 8, “On the Quantum Footpath” in D. D. Nolte, “Galileo Unbound: A Path Across Life, the Universe and Everything” (Oxford University Press, 2018)

For definitive accounts of Heisenberg’s life see D. Cassidy “Beyond Uncertainty: Heisenberg, Quantum Physics and the Bomb” (Bellevue Press, 2009)

References

[1] Heisenberg, W. (1925). “Über quantentheoretische Umdeutung kinematischer und mechanischer Beziehungen”. Zeitschrift für Physik, 33(1), 879–893.

[2] Born, M., & Jordan, P. (1925). “Zur Quantenmechanik”. Zeitschrift für Physik, 34(1), 858–888.

[3] Dirac, P. A. M. (1925). The fundamental equations of quantum mechanics. Proceedings of the Royal Society of London. Series A, Containing Papers of a Mathematical and Physical Character, 109(752), 642–653

[4] Born, M., W. Heisenberg and P. Jordan (1926). “Quantum mechanics II.” Zeitschrift Fur Physik, 35, (8/9): 557–615.

[5] Dirac, P. A. M. (1926). “Quantum mechanics and a preliminary investigation of the hydrogen atom.” Proceedings of the Royal Society of London Series A, 110(755): 561–79.

[6] Pauli, W. (1926). “The hydrogen spectrum from the view point of the new quantal mechanics.” Zeitschrift Fur Physik, 36(5): 336–63.

[7] Mensing, L. (1926). “Die Rotations-Schwingungsbanden nach der Quantenmechanik”. Zeitschrift für Physik, 36(11), 814–823.

[8] Born, M., & Oppenheimer, J. R. (1927). “Zur Quantentheorie der Molekeln”. Annalen der Physik, 389(20), 457–484.

Books by David Nolte at Oxford University Press
Read more in Books by David Nolte at Oxford University Press
Holonomy, Parallel Transport and Foucault's Pendulum
by David D. Nolte

Whole World Holonomy

Once upon a time the World was flat, and sailors feared falling off the edge if they sailed too far…at least that is how the fairy tale is told.

Flat World was a simple World.  Its inhabitants, the Flatworlders, carried vectors abount with them, vectors that were thick bundles of arrows, bound in a sheaf, that tended to point in a fixed direction.  In Flat World, once a vector had been oriented one way, it kept that orientation, no matter what path the Flatworlder took, always being exactly the same when it returned to its starting point.

Then came Cristobal Colon, and Carl Gauss and Bernhard Riemann, and Flat World became Round World, and the carrying around of vectors was no longer such a simple thing.  The surprising part was, when vectors returned to their starting point, even if they were carried with the greatest of care never to turn them or twist them, carrying them always parallel to themselves, they were never the same.  At the end of every different journey, they pointed in a different direction. 

How can this be?  How can a vector, that was transported always parallel to itself, end up pointing in a different direction when it was carried around a closed loop?

The answer is Holonomy!

Great Circle Routes

We were taught in Euclidean Geometry that the shortest path between two points is a straight line.  This lesson was fine for Flat World.  But now that we live in Round Riemann World, we know that the shortest distance between two points on the surface of the Earth is along a great circle route.  All great circles are Earth circumferences.  They are defined by three points: the starting point, the ending point and the center of the Earth.  The three points define a plane that intersects the surface of the Earth along a great circle.

Winkel Tripel projection of the Earth with flight path from Rio de Janeiro to Seoul, Korea.

Fig. 1. Great circle route from Rio de Janeiro, Brazil, to Seoul, Korea on a Winkel Tripel projection of the Earth.

The practical demonstration that great circles are shortest paths can be done with a string and a globe.  Pick any two points on the surface of the globe and stretch the string tightly between them so that the string lies taught on the surface of the globe.  If the two points are far enough apart (but no so far that they are nearly antipodal), then the string takes on the arc of a circle centered on the center of the globe.

Shortest paths on a curved surface, like a globe, are also known as geodesics.  And now that we have our geodesic paths for the Earth, we can start playing around with the parallel transportation of vectors.

Parallel Transport

The game is simple.  Start at the Equator with a vector that is pointing due North.  Now, move the vector due North along a line of longitude (a geodesic) until you hit the North Pole.  All the while, as you carry it along, the vector continues pointing due North on the surface of the Earth, never deviating.  When you reach the North Pole, take a sharp turn right by 90 degrees, being careful not to twist or turn the vector in any way.  Now, carry the vector with you due South along a new line of longitude until you hit the Equator, where again you take a sharp right turn by 90 degrees, and once again careful not to twist or turn the vector in any way.  Then return to your starting point. 

What you find, when you return home, is that the vector has turned through an angle of 90 degrees.   Despite how careful you were never to twist or turn it—it has turned nonetheless. This is holonomy.

Parallel transport around a segment of the sphere.
Fig. 2. Parallel transport around a geodesic triangle.Start at the equator with the vector pointing due North. Transport it without twisting it to the North Pole. Take a right turn, careful not to twist the vector, and proceed to the equator where you take another right turn and return to the starting point. Without ever twisting the vector, it has nonetheless rotated by 90-degrees over the closed path.

Holonomy

Holonomy, or more specifically Riemann holonomy, is the intrinsic twisting of vectors as they are transported parallel to themselves around a closed loop on a curved surface.  The twist is something “outside” of the local transport of the vector.  In the case of the Earth, this “outside” element is the curvature of the Earth’s surface.  Locally, the Earth looks flat, and the vector is moved so that it always points in the same direction.  But globally, the vector can slowly tilt as it moves along a geodesic path.

For the example of parallel transport on the Earth, look at the vector at its starting point and the vector when it reaches the North pole.  Clearly the vector has rotated by 90 degrees, even despite of, or actually because of, its perfect Northward orientation along the line of longitude.

In this specific example, the solid angle of the closed path is a perfect eighth part of the total 4π solid angle of the surface, or 4π/8 = π/2.  The angle by which the vector rotated on this path is precisely the same as the subtended solid angle.  This is no coincidence—it is the consequence of the Gauss-Bonnet Theorem.

This theorem holds for any arbitrary closed path because any path can be viewed as if it were made up of lots of little segments of great circles.  You can even pick a path that crosses itself, taking care to keep track of minus signs as solid angles add and subtract.  For example, a perfect figure eight, if followed around smoothly, has no holonomy, because the two halves cancel.

Here, alas, we must leave our simple geometric games with great circles on the globe. To delve deeper into the origins of holonomy, it is time to turn to differential geometry.

Differential Geometry

Differential geometry is the application of differential calculus to geometry, in particular to geometric subspaces, also known as manifolds.  A good example is the surface of a sphere embedded in three-dimensional space.  The surface of a sphere has intrinsic curvature, where the curvature is defined as the inverse of the radius of the sphere.

One of the cornerstones of differential geometry is the operator known as the covariant derivative.  It is defined as

This covariant derivative is a master at bookkeeping.  Notice how the item on the left has an a-up and a b-down, as does the first term on the right.  And if we think of the c-up and -down as canceling in the last term, then again we have a-up and b-down.  The small-case “del” on the right is the usual partial derivative of Va with respect to xb.  The second term on the right takes care of the intrinsic “twist” of the coordinates caused by curvature.  As a bookkeeping device, covariant derivatives take care of the variation of a function as well as of the underlying variation of the coordinate frame.  (The covariant derivative was crucial for Einstein when he was developing his General Theory of Relativity applied to gravity.)

One of the most important discoveries in differential geometry was may by Tullio Levi-Civita in 1917. Years before, Levi-Civita had helped develop tensor calculus with his advisor Gregorio Ricci-Curbastro at the University of Padua, and they published a seminal review paper in 1901 that Marcel Grossmann brought to Einstein’s attention when he was struggling to reconcile special relativity with gravity. Einstein and Levi-Civita corresponded in a series of famous letters in early 1915 as Einstein zeroed in on the final theory of General Relativity. Interestingly, that correspondence had as profound an effect on Levi-Civita as it had on Einstein. Once Einstein’s new theory was published in late 1915, Levi-Civita returned to tensor calculus to answer a critical question: What was the geometric meaning of the covariant derivative that was so crucial to the new theory of gravity?

To answer this question, Levi-Civita defined a new form of parallelism that held for vector fields on curved manifolds. The new definition stated that during the parallel transport of a vector along a path, its covariant derivative along that path vanishes. This definition is contained in the expression

where the ub on the left is the tangent vector of the path. Expanding this expression gives

and simplifying the first term yields the equation for parallel transport

For the surface of the sphere, with two variables θ and φ, these lead to two coupled ODEs

The Christoffel symbols for a spherical surface are

Earth Christoffel symbols.

Yielding the equations for Parallel Transport of a vector on the Earth

Parallel transport equations

These equations are all you need to calculate how much a vector rotates for any path taken across the face of the Earth.

Example: Parallel Transport Around a line of Latitude

One particularly simple path is a line of latitude. Lines of latitude are not geodesics (except for the Equator) and hence there will be a contribution to the twist of the vector caused by the curvature of the Earth. For lines of latitude, the equations of Parallel Transport become

The line element is

leading to the flow equations

where theta is fixed (in this case the angle relative to the North Pole) and φ is the dependent variable.

Rotation of a vector that has been parallel transported about a segment of a sphere.
Fig. 3. A vector that originally points due East on the 30th Parallel is rotated by 90-degrees during parallel transport, ending by pointing due South.

These copled ODEs are recognized as simple oscillations with the flow

and the initial value problem has the solution

where the angular frequency is the geometric mean of the coefficients

where λ is the latitude.

For a full rotation around a closed line of latitude, the parallel-transported vector components are

Foucault pendulum equations

As an example, take an initial vector [0, 1] pointing due East along the line of latitude. Then parallel-transport it around latitude 30o North. This gives the final vector the components

which is now pointing due South. The vector has been rotated by 90-degrees even though it was transported always parallel to itself on the surface of the Earth. The solid angle subtended by the 30-th parallel is exactly π/2.

One final bookkeeping step is needed. It looks like the magnitude of the vector changed during the transport: y0 = 1, but xf = cosλ. However, cosλ = sinθ, which is exactly the metric coefficient on the dφ term of the line element, and the vector retains its magnitude in spherical coordinates.

Foucault’s Pendulum

Holonomy is a subtle effect, and it’s hard to find good examples in real life where it matters. But there is one demonstration that almost anyone has seen, at least anyone with an interest in science: Foucault’s pendulum. This is the very long pendulum that is often found in science museums around the world. As the Earth turns, the plane of oscillation of the pendulum slowly turns, and the pendulum bob often knocks down blocks that the museum staff set up in the morning to track the precessing plane.

In a classical mechanics class, the precession of Foucault’s pendulum is usually derived through the effect of the Coriolis force on the moving pendulum bob. The answer for the precession frequency, after difficult integrations between non-inertial frames, is

Alternatively, the normal vector to the plane of oscillation can be viewed as parallel-transported around a closed loop at constant latitude. The amount of precession per day is

Precession rate of Foucault's pendulum.

which is exactly the same thing. Therefore, Foucault’s pendulum is a striking and exact physical demonstration of Whole World Holonomy.

Additional Reference: Physics Stack Exchange

Intersystem crossing (ISC) for singlet-to-triplet transition and generation of singlet oxygen
by David D. Nolte

A Story of Singlets and Triplets: Relativistic Biology

The tortoise and the hare.  The snail and the falcon.  The sloth and the cheetah.

Comparing the slowest animals to the fastest, the peregrine falcon wins in the air at 200 mph diving on a dove.  The cheetah wins on the ground at 75 mph running down dinner.  That’s fast!

Einstein’s theory of relativity says that fast things behave differently than slow things.  So how fast do things need to move to see these effects?

The measure is the ratio of the speed of the object relative to the speed of light at 670 million miles per hour.  This ratio is called beta

The cheetah has β = 1×10-7, and the peregrine falcon has β = 4×10-7—which are less than one part in a million. 

And what about that snail?  At a speed of 0.003 mph it has β = 4×10-12 for a just few parts per trillion.

Yet relativistic physics is present in biology, despite these slow speeds, and they can help keep us alive.  How?

The Boon and Bane of Oxygen

All animal life on Earth needs oxygen to survive.  Oxygen is the energy storehouse that fuels mitochondria—the tiny batteries inside our cells that generate the energetic molecules that make us run.

Of all the elements, oxygen is second only to flourine as the most chemically reactive.  But fluorine is too one-dimensional to help much with life.  It needs only one extra electron to complete its outer-shell octet, leaving nothing in reserve to attach to much else.  Oxygen, on the other hand, needs two electrons to complete its outer shell, making it an easy bridge between two other atoms, usually carbons or hydrogens, and there you have it—organic chemistry is off and running.

Yet the same chemical reactivity that makes oxygen central to life also makes it corrosive to life.  When oxygen is not doing its part keeping things alive, it is tearing things apart.

The problem is reactive oxygen species, or ROS.  These are activated forms of oxygen that damage biological molecules, including DNA, putting wear and tear on (aging) the cellular machinery and introducing mutations into the genetic codes.  And one of the ROS is an active form of simple diatomic oxygen O2 — the very air we breathe.

The Saga of the Singlet and the Triplet

Diatomic oxygen is deceptively simple: two oxygen atoms, each two electrons short of a full shell, coming together to share two of each other’s electrons in a double bond, satisfying the closed shell octet for the outer valence electrons for this element.

Fig. 1 The Lewis diagram of the oxygen double bond.  Each oxygen shares two electrons with the other, filling the valence shell.

Bonds are based on energy levels, and the individual energy levels of the two separate oxygen atoms combine and shift as they form molecular orbitals (MO).  These orbitals are occupied by the 6 + 6 = 12 electrons of the diatomic molecule.  The first 10 electrons fill up the lower MOs until the last two go into the next highest state.  Here, for interesting reasons associated with how electrons interact with each other in confined spaces, the last two electrons both have the same orientation of their spins.  The total electron spin of the final full ground-state configuration of 12 electrons has S = 1. 

The unreactive triplet ground state molecular orbital diagram of diatomic oxygen (dioxygen). The two last electron spins are unpaired.
Fig. 2 Molecular orbital diagram for diatomic oxygen.  The 2s and 2p levels of the separated oxygen hybridize into new orbitals that are filled with 6 + 6 = 12 electrons.  The last two electron states have the same spin with a total spin S = 1.  This is the unreactive triplet ground state.

When a many-electron system has a spin S = 1, quantum mechanics prescribes that it has 2S+1 spin projections, so that the ground state of diatomic oxygen has three possible spin projections—known as a triplet.  But this is just for the lowest energy configuration of O2.

It is also possible to put both electrons into the final levels with opposite spins, giving S = 0.  This is known as the singlet, and there are two different ways these spins can be anti-aligned, creating two excited states.  The first excited state is about 1 eV in energy above the ground state, and the second excited state is about 0.7 eV higher than the first. 

The spin excited states of diatomic oxygen showing the pairing of spins to produce reactive singlet oxygen.
Fig. 3 Ground and excited states of O2.  The two singlet excited states have paired electron spins with a total spin of S = 0.  The ground state has S = 1.  The transitions between ground and excited states are “spin forbidden”.

Now we come the heart of our story.  It hinges on how reactive the different forms of O2 are, and how easily the singlet and the triplet can transform into each other.

Don’t Mix Your Spins

What happens if you mix hydrogen and oxygen in a 2:1 ratio in a plastic bag?

Nothing!  Unless you touch a match to it, and then it “pops” and creates water H2O.

Despite the thermodynamic instability of oxygen and hydrogen, the mixture is kinetically stable because it takes an additional input of energy to make the reaction go.  This is because oxygen at room temperature is almost exclusively in its ground state, the triplet state.  The triplet oxygen accepts electrons from other molecules, or atoms like hydrogen, but the local environment of organic molecules are almost exclusively in S = 0 states because of their stability. To accept two electrons from organic molecules requires spins to flip, which has an energy associated with the process, creating an energy barrier. This is known as the spin conservation rule of organic chemistry. Therefore, the reaction with the triplet is unlikely to go, unless you give it a hand with extra energy or a catalyst to get over the barrier.

However, this “spin blockade” that makes triplet (S = 1) oxygen unreactive (kinetically stable) is lifted in the case of singlet (S = 0) oxygen.  The singlet still accepts two electrons from other molecules, but these can be taken up easily by accepting electrons from the S = 0 organic molecules around it, conserving spin.  This makes singlet oxygen extremely reactive organically and hence is why it is an ROS. Singlet oxygen reacts with organic molecules, damaging them.

Despite the deleterious effects of singlet oxygen, it is produced as a side effect of lipids (fats) immersed in an oxygen environment. In a sense, fat slowly “burns”, creating reactive organic species that further react with lipids (primarily polyunsaturated fatty acids (PUFAs)), generating more ROS and creating a chain reaction. The chain reaction is terminated by the Russell mechanism that generates singlet oxygen as a byproduct.

Singlet oxygen, even though it is an excited state, cannot convert directly back to the benign triplet ground state for the same spin conservation reasons as organic chemistry. The singlet (S = 0) cannot emit a photon to get to its ground state triplet (S = 1) because photons cannot change the spin of the electrons in a transition. So once the singlet oxygen is formed, it can stick around and react chemically, eating up an organic molecule.

Therefore, the oxygen environment we are immersed in, so necessary for our survival, is slowly killing us with oxidative stress. In response, mechanisms to de-excite singlet oxygen evolved, using organic molecules like carotenoids that are excellent physical quenchers of the singlet state. How does this happen? Enter Einstein’s theory of special relativity.

Relativistic Origins of Spin-Orbit Coupling

When I was a sophomore at Cornell University in the late 1970’s, I took the introductory class in electricity and magnetism. The text was an oddball thing from the Berkeley Physics Series authored by the Nobel Laureate, Edward Purcell, from Harvard.

Cover and front page of Purcell's E&M volume of the Berkeley Series.
Fig. 4 The cover and front page of my 1978 copy of Edward Purcell’s Berkeley Physics volume on Electricity and Magnetism.

(The Berkeley Series was a set of 5 volumes to accompany a 5-semester introduction to physics. It was the brainchild of Charles Kittel from Berkeley and Philip Morrison from Cornell who, in 1961, were responding to the Sputnik crisis and the need to improve the teaching of physics in the West.)

Purcell’s book had the quirky misfortune to use Gaussian units based on centimeters and grams (cgs) instead of meters and kilograms (MKS). Physicists tend to like cgs units, especially in the teaching of electromagnetism, because it places electric fields and magnetic fields on equal footing. Unfortunately, it creates a weird set of units like “statvolts” and “statcoulombs” that are a nightmare to calculate with.

Nonetheless, Purcell’s book was revolutionary as a second-semester intro physics book, in that it used Special Relativity to explain the transformations between electric and magnetic fields. For instance, starting with the static electric field of a stationary parallel plate capacitor in one frame, Purcell showed how an observer moving relatively to the capacitor in a moving frame detects the electric field as expected, but also detects a slight magnetic field. As the speed of the observer increases, the strength of the magnetic field increases, becoming comparable to the electric field in strength as the relative frame speed approaches the speed of light.

In this way, there is one frame in which there is no magnetic field at all, and another frame in which there is a strong magnetic field. The only difference is the point of view—yet the consequences are profound, especially when the quantum spin of an electron is involved.

Conversion of E fields to B fields through relativistically moving frames
Fig. 5 Purcell’s use of a parallel plate capacitor in his demonstration of the origin of magnetic fields from electric fields in relatively moving frames.

The spin of the electron is like a tiny magnet, and if the spin is in an external magnetic field, it feels a torque as well as an interaction energy. The torque makes it precess, and the interaction energy shifts its energy levels depending on the orientation of the spin to the field.

When an electron is in a quantum orbital around a stationary nucleus, attracted by the electric field of the nucleus, it would seem that there is no magnetic field for the spin to interact with, which indeed is true if the electron has no angular momentum. But if the electron orbital does have angular momentum with a non-zero expectation value for its velocity, then this moving electron does experience a magnetic field—the electron is moving relative to the electric field of the nucleus, and special relativity dictates that it experiences a magnetic field. The resulting magnetic field interacts with the magnetic moment of the electron and shifts its energy a tiny amount.

Spin-orbit coupling and spin-forbidden transitions. Spin-orbit mixes singlet and triplet spin states.
Fig. 6 Transitions to the singlet excited state are allowed but to the triplet state are spin-forbidden. The spin-orbit coupling mixes the spin states, giving a little triplet character to the singlet and vice versa

This is called the spin-orbit interaction and leads to the fine structure of the electron energy levels in atoms and molecules. More importantly for our story of Singlets and Triplets, the slight shift in energy also mixes the spin states. Quantum mechanical superposition of states mixes in a little S = 0 into the triplet excited state and a little S = 1 into the singlet ground state, and the transition is no longer strictly spin forbidden. The spin-orbit effect is relatively small in oxygen, contributing little to the quenching of singlet oxygen. But spin-orbit in other molecules, especially dye-like organic molecules, can be strong, creating a protective antioxidant mechanism to remove singlet oxygen.

Relativistic Biology: Antioxidants

Do you eat blueberries? Or carrots? Or other brightly colored foods? If so, you are enlisting relativistic biology to help keep you healthy. These fruits and vegetables are colored because they contain organic molecules that absorb certain wavelengths of light but not others, giving them their strong colors. The same organic complexes that absorb light are also good at interacting with singlet oxygen, taking the singlet spin onto themselves while converting the oxygen back to its benign triplet.

With the reactive oxygen singlet gone, the organic singlet still has stored energy that must be dissipated. This happens through intersystem crossing allowed by the spin-orbit coupling (relativistic biology), converting the antioxidant to its triplet state that can de-excite through normal vibrational processes, harmlessly releasing the energy as heat that diffuses away.

Antioxidant molecules like the carotenoids, that color food, accept the singlet spin state from the oxygen and de-excite through intersystem crossing and thermal dissipation. Other antioxidants, like vitamin E (tocopherols) and amines, provide high electron density directly to the singlet oxygen, enhancing the otherwise weak spin-orbit effect of isolated oxygen, allowing the oxygen to convert back to it triplet ground state. For both of these types of antioxidants, the molecule is unaltered chemically by this process, and they keep sweeping up reactive singlet oxygen, removing them from the local biological environment and protecting your health.

But let’s flip the problem of the singlet oxygen, and rather than get rid of it, ask what it takes to selectively harness singlet oxygen production to act as a targeted therapy to kill cancer cells.

Relativistic Biology: Photodynamic Cancer Therapy

The physics of light propagation through living tissue is a fascinating topic. Light is easily transported through tissue through multiple scattering. This is why your whole hand glows red when you cover a flashlight at night. The photons bounce around but are not easily absorbed. This surprising translucence of tissue can be used to help treat cancer.

Photodynamic cancer therapy uses photosensitizer molecules, typically organic dyes, that absorb light, transforming the molecule from a singlet ground state to a singlet excited state (spin-allowed transition). Although singlet-to-triplet conversion is spin-forbidden, the spin-orbit coupling slightly mixes the spin states which allows a transformation known as intersystem crossing (ISC). The excited singlet crosses over (usually through a vibrational state associated with thermal energy) to an excited triplet state of the photosensitizer molecule. Oxygen triplet molecules, that are always prevalent in tissue, collide with the triplet photosensitizer—and they swap their energies in a spin-allowed transfer. The photosensitizer triplet returns to its singlet ground state, while the triplet oxygen converts to highly reactive singlet oxygen. The swap doesn’t change total spin, so it is allowed and fast, generating large amounts of reactive oxygen singlets.

Intersystem crossing (ISC) for singlet-to-triplet transition and generation of singlet oxygen
Fig. 7 Intersystem crossing diagram. A photosensitizer molecule in a singlet ground state absorbs a photon that creates a singlet excited state of the molecule. The spin-orbit mixing of spin states allows intersystem crossing (ISC) to generate a triplet excited state of the photosensitizer. This triplet can then exchange its energy with oxygen to create highly-reactive singlet oxygen.

In photodynamic therapy, the photosensitizer is taken up by the patient’s body, but the doctor only shines light around the tumor area, letting the light multiply-scatter through the tissue, exciting the photosensitizer and locally producing singlet oxygens that kill the local cancer cells. Other parts of the body remain in the dark and have none of the ill-effects that are so common for the conventional systemic cytotoxic anti-cancer drugs. This local treatment of the tumor using localized light can be much more benign to overall patient health while still delivering effective treatment to the tumor.

Photodynamic therapy has been approved by the FDA for some early stage cancers, and continuing research is expanding its applications. Because light transport through tissue is limited to about a centimeter, most of these applications are for “shallow” tumors that can be accessed by light through the skin or through internal surfaces (like the esophagus or colon).

Postscript: Relativistic Spin

I can’t leave this story of relativistic biology without going into a final historical detail from the early days of relativistic quantum theory. When Uhlenbeck and Goudsmit first proposed in 1925 that the electron has spin, there were two immediate objections. First, Lorentz showed that in a semiclassical model of the spinning electron, the surface of the electron would be moving at 300 times the speed of light. The solution to this problem came three years later in 1928 with the relativistic quantum theory of Paul Dirac, which took an entirely different view of quantum versus classical physics. In quantum theory, there is no “radius of the electron” as there was in semiclassical theory.

The second objection was more serious. The original predictions from electron spin and the spin-orbit interaction in Bohr’s theory of the atom predicted a fine-structure splitting that was a factor of 2 times larger than observed experimentally. In 1926 Llewellyn Thomas showed that a relativistically precessing spin was in a non-inertial frame, requiring a continuous set of transformations from one instantaneously inertial frame to another (a mathematical phenomenon related to parallel transport known as holonomy). These continuously shifting transformations introduced a factor of 1/2 into the spin precession, exactly matching the experimental values. This effect is known as Thomas precession. Interestingly, the fully relativistic theory of Dirac in 1928 automatically incorporated this precession within the theory, so once again Dirac’s equation superseded the old quantum theory.

Examples of conformal maps with transform functions for field lines and potentials.
by David D. Nolte

The Craft of Conformal Maps

Somewhere, within the craft of conformal maps, lie the answers to dark, difficult problems of physics.

For instance, can you map out the electric field lines around one of Benjamin Franklin’s pointed lightning rods?

Can you calculate the fluid velocities in a channel making a sharp right angle?

Now take it up a notch in difficulty: Can you find the distribution of the sizes of magnetic domains within a flat magnet that is about to depolarize?

Or take it to the max: Can you find the vibration frequencies of the cosmic strings of string theory?

The answers to all these questions starts with simple physics solutions within simple boundaries—sometimes a problem so simple even a freshman physics student can solve it—and then mapping the solution, point by point, onto the geometry of the desired problem.

Once the right mapping function is found, you can solve some of the stickiest, ugliest, crankiest problems of physics like a pro.

The Earliest Conformal Maps

What is a conformal map?  It is a transformation that takes one picture into another, keeping all local angles unchanged, no matter how distorted the overall transformation is.

This property was understood by the very first mathematicians, wrangling their sexagesimal numbers by the waters of Babylon as they mapped the heavens onto charts to foretell the coming of the seasons.

Sterographic projection of the celestial sphere onto a plane
Fig. 1 Geometry of stereographic projection

Hipparchus of Rhodes, around 150 BCE during the Hellenistic transition from Alexander to Caesar, was the first to describe the stereographic projection by which the locations of the stars were mapped on a plane by locating all the stars on the celestial sphere and tracing a line from the bottom of the sphere to the star and plotting where the line intersects the mid plane.  Why this method should be conformal, preserving the angles, was probably beyond his mathematical powers, but he probably intuitively knew that it did.

Astrolabe map of the stars based on stereographic projection
Fig. 2 An astrolabe for the location of Brussels, Belgium, generated by a stereographic projection

Ptolemy of Alexandria around 150 CE, expanded on Hipparchus’ star charts and then introduced his own conical-like projection to map all the known world of his day.  The Ptolemaic projection is almost conformal, but not quite.  He was more interested in keeping areas faithful than angles.

Ptolemy's map of the world as reconstructed in the Renaissance.
Fig. 3 A Renaissance rendering of Ptolemy’s map of the known world in pseudo-conic projection.

Mercator’s Rules of Rhumb

The first conformal mapping of the Earth’s surface onto the plane was constructed by Gerard Mercator in 1569.  His goal, as a map maker, was to construct a map that traced out a ship’s course of constant magnetic bearing as a straight line, known as a rhumb line.  This mapping property had important utility for navigators, especially on long voyages at sea beyond the sight of land, and was a hallmark of navigation maps of the Mediterranean, known as Portolan Charts.  Rhumb lines were easy to draw on the small scales of the middle ocean, but on the scale of the Earth, no one knew how to do it.

Mercator's North Atlantic map
Fig. 4 Mercator’s North Atlantic with compass roses and rhumb lines. (Note the fictitious islands south of Iceland and the large arctic continent north of Greenland.)

Though Mercator’s life and career have been put under the biographer’s microscope numerous times, the exact moment when he realized how to make his map—the now-famous Mercator Projection—is not known.  It is possible that he struck a compromise between a cylindrical point projection, that stretched the arctic regions, and a cylindrical line projection that compressed the arctic regions.  He also was a maker of large globes on which rhumb lines (actually curves) could be measured and transferred to a flat map.  Either way, he knew that he had invented something entirely new, and he promoted his map as an aid for the Age of Exploration.  There is some evidence that Frobisher took Mercator’s map with him during his three famous arctic expeditions seeking the Northwest Passage.

Mercator projection of the Earth
Fig. 5 Modern Mercator conformal projection of the Earth.

Mercator never explained nor described the mathematical function behind his projection.  This was first discovered by the English mathematician Thomas Harriot in 1589, 20 years after Mercator published his map, as Harriot was helping Sir Walter Rayleigh with his New World projects.  Like most of what Harriot did during his lifetime, he was years (sometimes decades) ahead of anyone else, but no one ever knew because he never published.  His genius remained buried in his personal notes until they were uncovered in the late 1800’s long after others had claimed credit for things he did first.

The rhumb lines of Mercator’s map maintain constant angle relative to all lines of longitude and hence the Mercator projection is a conformal map.  The mathematical proof of this fact was first given by James Gregory in 1668 (almost a century after Mercator’s feat) followed by a clearer proof by Isaac Barrow in 1670.  It was 25 years later that Edmund Halley (of Halley’s Comet fame) proved that the stereographic projection was also conformal.

A hundred years passed after Halley before anyone again looked into the conformal properties of mapping—and then the field exploded.

The Rube in Frederick’s Berlin

In 1761, the Swiss contingent of the Prussian Academy of Sciences nominated a little-known self-taught Swiss mathematician to the membership of the Academy.  The process was pro forma, but everyone nominated was interviewed personally by Frederick the Great who had restructured the Academy years before from a backwater society to a leading scientific society in Europe.  When Frederick met Johann Lambert, he thought it must be a practical joke.  Lambert looked strange, dressed strangely, and his manners were even stranger.  He was born poor, had never gone to school, and he looked it and he talked it. 

Portrait of Johann Heinrich Lambert
Fig. 6 Portrait of Johann Heinrich Lambert

Frederick rejected the nomination.

But the Swiss contingent, led by Leonhard Euler himself, persisted, because they knew what Frederick did not—Lambert was a genius.  He was an autodidact who had pulled himself up so thoroughly, that he had self-published some of the greatest works of philosophy and science of his generation.  One of these was on the science of optics which established standards of luminance that we still use today.  (In my own laboratory, my students and I routinely refer to Lambertian surfaces in our research on laser speckle.  And we use the Lambert-Beer law of optical attenuation every day in our experiments.)

Frederick finally relented after a delay of two years, and admitted Lambert to his Academy, where Lambert went on a writing rampage, publishing a paper a month over the next ten years, like a dam letting loose.

One of Lambert’s many papers was on projection maps of the Earth.  He not only picked up where Halley had left off a hundred years earlier, but he invented 7 new projections, three of which were conformal and four of which were equal area.  Three of Lambert’s projections are in standard use today in cartography. 

The Lambert conformal conic projection of the Earth
Fig. 7 The Lambert conformal conic projection centered on the 36th parallel.

Although Lambert worked at the time of Euler, Euler’s advances in complex-valued mathematics was still young and not well known, so Lambert worked his projections using conventional calculus.  It would be another 100 years before the power of complex analysis was brought fully to bear on the problem of conformal mappings.

Riemann’s Sphere

It seems like the history of geometry can be divided into two periods: the time before Bernhard Riemann and the time after Bernhard Riemann. 

Bernhard Riemann portrait
Fig. 8 Bernhard Riemann.

Bernhard Riemann was a gentle giant, a shy and unimposing figure with a Herculean mind.  He transformed how everyone thought about geometry, both real and complex.  His doctoral thesis was the most complete exposition to date on the power of complex analysis, and his Habilitation Lecture on the foundations of geometry shook those very foundations to their core.

In the hands of Riemann, the stereographic projection became a complex transform of the simplest type

where x, y and z are the spherical coordinates of a point on the sphere.

Riemann sphere projection as a conformal map
Fig. 9 Conformal mapping of the surface of the Riemann sphere onto the complex plane.

The projection in Fig. 9 is from the North Pole, which represents Antarctica faithfully but distorts the lands of the Northern Hemisphere. Any projection can be centered on a chosen point of the Earth by projecting from the opposite point, called the antipode. For instance, the stereographic projection centered on Chicago is shown in Fig. 10.

Stereographic projection centered on Chicago.
Fig. 10 Stereographic projection centered on Chicago, Illinois. Note the size of Greenland relative to its size in the Mercator projection of Fig. 5.

Building on the work of Euler and Cauchy, Riemann dove into conformal maps and emerged in 1851 with one of the most powerful theorems in complex analysis, known as the Riemann Mapping Theorem:

Any non-empty, simply connected open subset of the complex plane (which is not the entire plane itself) can be conformally mapped to the open unit disk. 

An immediate consequence of this is that all non-empty, simply connected open subsets of the complex plane are equivalent, because any domain can be mapped onto the unit disk, and then the unit disk can be mapped to any domain.

The consequences of this are astounding:  Solve a simple physics problem in a simple domain and then use the Riemann mapping theorem to transform it into the most complex, ugly, convoluted, twisted problem you can think of (as long as it is simply connected) and then you have the answer.

The reason that conformal maps (that are purely mathematical) allow the transformation of physics problems (that are “real”) is because physics is based on orthogonal sets of fields and potentials that govern how physical systems behave.  In other words, the solution to the Laplacian operator on one domain can be transformed to a solution of the Laplacian operator on a different domain.

Powerful! Great!  But how do you do it?  Riemann’s theorem was an existence proof—not a solution manual.  The mapping transformations still needed to be found.

Schwarz-Christoffel

On the heels of Bernard Riemann, who had altered the course of geometry, Hermann Schwarz at the University of Halle, Germany, and Elwin Bruno Christoffel at the Technical University in Zürich, Switzerland, took up Riemann’s mapping theorem to search for the actual mappings that would turn the theorem from “nice to know” to an actual formula.

Working independently, Christoffel in 1867 drew on his expertise in differential geometry while Schwarz in 1869 drew on his expertise in the calculus of variations, both with a solid background in geometry and complex analysis.  They focused on conformal maps of polygons because general domains on the complex plane can be described with polygonal boundaries.  The conformal map they sought would take simple portions of the complex plane and map them to the interior angle of a polygonal vertex.  With sufficient constraints, the goal was to map all the vertexes and hence the entire domain.

The surprisingly simple result is known as the Schwarz-Christoffel equation

where a, b, c … are the positions of the vertices, and α, β, γ … are the interior angles of the vertices.  The integral needs to be carried out on the complex plane, but it has closed-form solutions for many common cases.

This equation solves the problem of “how” that allows any physics solution on one domain to be mapped to another domain.

Conformal Maps

The list of possible conformal maps is literally limitless, yet there are a few that are so common that they deserve to be explored in some detail here.

One conformal map is so “famous” it has the name of the Joukowski Map that takes the upper half plane and transforms it (through an open strip) onto the full complex plane. The field lines and potentials are shown in Fig. 11 as a simple transform of straight lines. To calculate these fields and potentials directly would require the solution of a partial differential equation (PDE) through numerical methods.

Field and potential lines near an aperture in conducting plates by a conformal map.
Fig. 11 Field lines and potentials around a gap in a charged conductor by the Joukowski conformal map.

Other common conformal maps are power-law transformations, taking the upper half plane into the full plane. Fig. 12 shows three of these, the first an inner half corner, the second the outer half corner, and the third transforming the upper half plane onto the full plane. All three of these show the field lines and the potentials near charged conducting plates.

Conformal maps from the half-plane to the full plane with field and potential lines.
Fig. 12 Maps from the half-plane to the full plane: a) Inner corner, b) outer corner, c) charged thin plate.

Conformal maps can also be “daisy-chained”. For instance, in Fig. 13, the unit circle is transformed into the upper half plane, providing the field lines and equipotentials of a point charge near a conducting plate. The fields are those of a point charge and its image charge, creating a dipole potential. This charge and its image are transformed again into the fields and potentials of a point charge near a conducting corner.

Compound conformal maps of the unit circle to the half-plane to the outside of a corner.
Fig. 13 Point charge fields and potentials near a conducting corner by a compound conformal map: a) Unit circle to the half-plane, b) Half-plane to the outside corder.

But we are not quite done with conformal maps. They have reappeared in recent years in exciting new areas of physics in the form of conformal field theory.

Conformal Field Theory

The importance being conformal extends far beyond solutions to Laplace’s equation.  Physics is physics, regardless of how it comes about and how it is described, and transformations cannot change the physics.  As an example, when a many-body system is at a critical point, then the description of the system is scale independent.  In this case, changing scale is one type of transformation that keeps the physics the same.  Conformal maps also keep the physics the same by preserving angles.  Taking this idea into the quantum realm, a quantum field theory of a scale-invariant system can be conformally mapped onto other, more complex systems for which answers are not readily derived. 

This is why conformal field theory (CFT) has become an important new field of physics with applications ranging as widely as quantum phase transitions and quantum strings.

Books by David Nolte at Oxford University Press
Read more in Books by David D. Nolte at Oxford University Press.

by David D. Nolte

Anant K. Ramdas in the Golden Age of Physics

The physicist, as a gentleman and a scholar, who, in his leisure, pursues physics as both vocation and hobby, is an endangered species, though they once were endemic.  Classic examples come from the turn of the last century, as Rayleigh and de Broglie and Raman built their own laboratories to follow their own ideas.  These were giants in their fields. But there are also many quiet geniuses, enthralled with the life of ideas and the society of scientists, working into the late hours, following the paths that lead them forward through complex concepts and abstract mathematics as a labor of love.

One of these quiet geniuses, of late, was a colleague of mine and a friend, Anant K. Ramdas.  He was the last PhD student of the Nobel Prize Laureate, C. V. Raman, and he may have been the last of his kind as a gentleman and a scholar physicist.

Anant K. Ramdas

Anant Ramdas was born in May, 1930, in Pune, India, not far from the megalopolis of Mumbai when it had just over a million inhabitants (the number is over 22 million today, nearly a hundred years later).  His father, Lakshminarayanapuram A. Ramdas, was a scientist, a meteorologist who had studied under C. V. Raman at the University of Calcutta.  Raman won the Nobel Prize in Physics the same year that Anant Ramdas was born. 

Ramdas received his BS in Physics from the University of Pune in 1950, then followed in his father’s footsteps by studying for his MS (1953) and PhD (1956) degrees in Physics under Raman, who had established the Raman Institute in Bangalore, India. 

While facing the decision, after his graduation, on what to do and where to go, Ramdas read a review article published by Prof. H. Y. Fan of Purdue University on infrared spectroscopy of semiconductors.  After corresponding with Fan, and with the Purdue Physics department head, Prof. Karl Lark-Horowitz, Ramdas decided to accept the offer of a research associate (a post-doc position), and he prepared to leave India.

Within only a few months, he met and married his wife, Vasanti, and they hopped on a propeller plane to London that stopped along the way in Cairo, Beirut, Lebanon, and Paris before arriving in London.  From there, they caught a cargo ship making a two-week passage across the Atlantic, after stopping at ports in France and Portugal.  In New York City, they took a train to Chicago, getting off during a brief stop in the little corn-town of Lafayette, Indiana, home of Purdue University.  It was 1956, and Anant and Vasanti were, ironically, the first Indians that some people in the Indiana town had ever seen.

Semiconductor Physics at Purdue

Semiconductors became the ascendent electronic material during the Second World War when it was discovered that their electrical properties were ideal for military radar applications.  Many of the top physicists of the time worked at the “Rad Lab”, the Radiation Laboratory of MIT, and collaborations spread out across the US, including to the Physics Department at Purdue University.  Researchers at Purdue were especially good at growing the semiconductor Germanium, which was used in radar rectifiers.  The research was overseen by Lark-Horowitz.

After the war, semiconductor research continued to be a top priority in the Purdue Physics department as groups around the world competed to find ways to use semiconductors instead of vacuum tubes for information and control.  Friendly competition often meant the exchange of materials and samples, and sometime in early 1947, several Germanium samples were shipped to the group of Bardeen and Brattain at Bell Labs, where, several months later, they succeeded in making the first point contact transistor using Germanium (with some speculation today that it may have been with the samples sent from Purdue).  It was a close thing. Ralph Bray, a professor at Purdue, had seen nonlinear current dependences in the Purdue-grown Germanium samples that were precursers of transistor action, but Bell made the announcement before Bray had a chance to take the next step. Lark-Horowitz (and Bray) never forgot how close Purdue had come to making the invention themselves [1].

Bray_1997_Electrochem._Soc._Interface_6_24Download

In 1948, Lark-Horowitz hired H. Y. Fan, who had received his PhD at MIT in 1937 and had been teaching at Tsinghua University in China.  Fan was an experimental physicist specializing in the infrared properties of semiconductors, and when Ramdas arrived at Purdue in 1956, he worked directly under Fan.  They published their definitive work on the infrared absorption of irradiated silicon in 1959 [2].

Absorption spectrum of “effective-mass” shallow defect levels in irradiated silicon.

FanRamdasDownload

One day, while Ramdas was working in Fan’s lab, Lark-Horowitz stopped by, as he was accustomed to do, and he casually asked if Ramdas would be interested in becoming a professor at Purdue.  Ramdas of course said “Yes”, and Lark-Horowitz gave him the job on the spot.  Ramdas was appointed as an assistant professor in 1960.  These things were less formal in those days, and it was only later that Ramdas learned that Fan had already made a strong case for him.

The Golden Age of Physics

The period from 1960 to 2015, which spanned Ramdas’ career, start to finish, might be called “The Golden Age of Physics”. 

This time span saw the completion of the Standard Model of particle physics with the theory of quarks (1964), the muon neutrino (1962), electro-weak unification (1968), quantum chromodynamics (1970s), the tau lepton (1975), the bottom quark (1977), the top quark (1995), the W and Z bosons (1983), the tau neutrino (2000), neutrino mass oscillations (2004), and of course capping it off with the detection of the Higgs boson (2012). 

This was the period in solid state physics that saw the invention of the laser (1960), the quantum Hall effect (1980), the fractional quantum Hall effect (1982), scanning tunneling microscopy (1981), quasi-crystals (1982), high-temperature superconductors (1986), and graphene (2005).

This was also the period when astrophysics witnessed the discovery of the Cosmic Background Radiation (1964), the first black hole (1964), pulsars (1967), confirmation of dark matter (1970s), inflationary cosmology (1980s), Baryon Acoustic Oscillations (2005), and capping the era off with the detection of gravitational waves (2015).

The period from 1960 – 2015 stands out relative to the “first” Golden Age of Physics from 1900 – 1930 because this later phase is when the grand programs from early in the century were brought largely to completion.

But these are the macro-events of physics from 1960-2015.  This era was also a Golden Age in the micro-events of the everyday lives of the physicists.  It is this personal aspect where this later era surpassed the earlier era (when only a handful of physicists were making progress).  In the later part of the century, small armies of physicists were advancing rapidly along all the frontiers at the same time, and doing it with the greatest focus.

This was when a single NSF grant could support a single physicist with several grad students and an undergraduate or two.  The grants could be renewed with near certainty, as long as progress was made and papers were published.  Renewal applications, in those days, were three pages.  Contrast that to today when 25 pages need to be honed to perfection—and then the renewal rate is only about 10% (soon to be even lower with the recent budget cuts to science in the USA).  In those earlier days, the certainty of success, and the absence of the burden of writing multiple long grant proposals, bred confidence to dispose of the conventional, to try anything new.  In other words, the vast amount of time spent by physicists during this Golden Age was in the pursuit of physics, in the classroom and in the laboratory.

And this was the time when Anant Ramdas and his cohort—Sergio Rodriguez, Peter Fisher, Jacek Furdyna, Eugene Haller, the Chandrasekhar’s, Manuel Cardona, and the Dresselhaus’s—rode the wave of semiconductor physics when money was easy, good students were plentiful, and a vibrant intellectual community rallied around important problems.

Selected Topics of Research from Anant Ramdas

It is impossible to give justice to the breadth and depth of research performed by Anant over his career. So here is my selection of some of my favorite examples of his work:

Diamond

Anant had a life-long fascination for diamonds. As a rock and gem collector, he was fond of telling stories about the famous Cullinan diamond (weighed 1.3 pounds as a raw diamond at 3000 carats) and the blue Hope diamond (discovered in India). One of his earliest and most cited papers was on the Raman spectrum of Diamond [3], and he published several papers on his favorite color for diamonds—Blue [4]!

Raman Spectrum of Diamond.

DiamondPhysRevB.1.1687Download

His work on diamond helped endear Anant with the husband-wife team of Milly Dresselhaus and Gene Dresselhaus at MIT. Milly was the “Queen” of carbon, known for her work on graphite, carbon nanotubes and Fullerenes. Purdue had made an offer of an assistant professorship to Gene Dresselhaus when the two were looking for faculty positions after their post-docs at the University of Chicago, but Purdue would not give Milly a position (she was viewed as a “trailing” spouse). Anant was already at Purdue at that time and got to know both of them, maintaining a life-long friendship. Milly went on to become the president of the APS and was elected a member of the National Academy of Sciences, the National Academy of Engineering and the American Academy of Arts and Sciences.

Magneto-Optics

Purdue was a hot-bed of II-VI semiconductor research in the 1980’s, spearheaded by Jacek Furdyna. The substitution of the magnetic ion Mn for Zn, Cd or Hg created a unique class of highly magnetic semiconductors. Anant was the resident expert on the optical properties of the materials and collected one of the best examples of Giant Faraday Rotation [5].

Giant Faraday Effect in CdMnTe

FaradayPhysRevBDownload

Anant and the Purdue team were the world leaders in the physics and materials science of diluted magnetic semiconductors.

Shallow Defects in Semiconductors

My own introduction to Anant was through his work on shallow effective-mass defect states in semiconductors. I was working towards my PhD with Eugene ‘Gene” Haller at Lawrence Berkeley Lab (LBL) in the early 1980’s, and Gene was an expert on the spectroscopy of the shallow levels in Germanium. My co-physics graduate student colleague was Joe Kahn, and the two of us were tasked with studying the review article that Anant had written with his long-time theoretical collaborator Sergio Rodriguez on the physics of effective-mass shallow defects in semiconductors [6]. We called it “The Bible”, and spent months studying it. Gene Haller’s principal technique was photothermal ionization spectroscopy (PTIS), and Joe was building the world’s finest PTIS instrument. Joe met Anant for dinner one night at the March meeting of the APS in 1986, and when he got back to the room, he waxed poetic about Anant for an hour. It was like he had met his hero. I don’t remember how I missed that dinner, so my personal introduction to Anant Ramdas would have to wait.

PTIS spectra of donors in GaAs

Ramdas_1981_Rep._Prog._PhysDownload

My own research went into deep-level transient spectroscopy (DLTS) working with Gene and his group theorist, Wladek Walukiewicz, where we discovered a universal pressure derivative in III-V semiconductors. This research led me to a post-doc position at Bell Labs under Alastair Glass and later to a faculty position at Purdue, where I did finally meet Anant, who became my long-time champion and mentor. But Joe had stayed with the shallow defects, and in particular defects that showed interesting dynamical properties, known as tunneling defects.

Dynamic Defects in Semiconductors

Dynamic defects in semiconductors are multicomponent defects (often involving vacancies or interstitial defects) in which one of the components tunnels quantum mechanically, or hops, rapidly on a time scale short compared to the measurement interaction time (electric dipole transition), so that the measurement sees increased symmetry compared to the instantaneous low-symmetry configuration of the defect.

Eugene Haller and his physics theory collaborator, Leo Falicov, were pioneers in tunneling defects related to hydrogen, building on earlier work by George Watkins who studied dynamical defects using EPR measurements. In my early days doing research under Eugene, we thought we had discovered a dynamical effect in FeB defects in silicon, and I spent two very interesting weeks at Lehigh University, visiting Watkins, to test out our idea, but it turned out to be a static effect. Later, Joe Kahn found that some of the early hydrogen defects in Germanium that Gene and Leo had proposed as dynamical defects were also, in fact, static. So the class of dynamical defects in semiconductors was actually shrinking over time rather than expanding. Joe did go on to find clear proof of a hydrogen-related dynamical defect in Germanium, saving the Haller-Falicov theory from the dust bin of Physics History.

In 2006 and in 2008, Ramdas was working on Oxygen-related defect complexes in CdSe when his student, G. Chen [7-8], discovered a temperature-induced symmetry raising. It showed clear evidence for a lower symmetry defect that converged into a higher symmetry mode at high temperatures, very much in agreement with the Haller-Falicov theory of dynamical symmetry raising.

At that time, I was developing my course notes for my textbook Introduction to Modern Dynamics, where some of the textbook problems in synchronization looked just like Anant’s data. Using a temperature-dependent coupling in a model of nonlinear (anharmonic) oscillators, I obtained the following fits (solid curves) to the Ramdas data (data points):

Quantum synchronization in CdSe and CdTe.

DoubletPhysRevLettDownload
TripletPhysRevLettDownload

The fit looks too good to be a coincidence, and Anant and I debated on whether the Haller-Falicov theory, or a theory based on nonlinear synchronization, would be better descriptions of the obviously dynamical properties of these defects. Alas, Anant is now gone, and so are Gene and Leo, so I am the last one left thinking about these things.

Beyond the Golden Age?

Anant Ramdas was fortunate to have spent his career during the Golden Age of Physics, when the focus was on the science and on the physics, as healthy communities helped support one another in friendly competition. He was a gentleman scholar, an avid reader of books on history and philosophy, much of it (but not all) on the history and philosophy of physics. His “Coffee Club” at 9:30 AM every day in the Physics Department at Purdue was a must-not-miss event that was attended by all of the Old Guard as well as by myself, where the topics of conversation ran the gamut, presided over by Anant. He had his NSF grant, year after year (and a few others), and that was all he needed to delve into the mysteries of the physics of semiconductors.

Is that age over? Was Anant one of the last of that era? I can only imagine what he would say about the current war against science and against rationality raging across the USA right now, and the impending budget cuts to all the science institutes. He spent his career and life upholding the torch of enlightenment. Today, I fear he would be holding it in the dark. He passed away Thanksgiving, 2024.

Vasanti and Anant, 2022.

References

[1] Ralph Bray, “A Case Study in Serendipity”, The Electrochemical Society, Interface, Spring 1997.

[2] H. Y. Fan and A. K. Ramdas, “INFRARED ABSORPTION AND PHOTOCONDUCTIVITY IN IRRADIATED SILICON,” Journal of Applied Physics, Article vol. 30, no. 8, pp. 1127-1134, 1959, doi: 10.1063/1.1735282.

[3] S. A. Solin and A. K. Ramdas, “RAMAN SPECTRUM OF DIAMOND,” Physical Review B, Article vol. 1, no. 4, pp. 1687-&, 1970, doi: 10.1103/PhysRevB.1.1687

[4] H. J. Kim, Z. Barticevic, A. K. Ramdas, S. Rodriguez, M. Grimsditch, and T. R. Anthony, “Zeeman effect of electronic Raman lines of accepters in elemental semiconductors: Boron in blue diamond,” Physical Review B, Article vol. 62, no. 12, pp. 8038-8052, Sep 2000, doi: 10.1103/PhysRevB.62.8038.

[5] D. U. Bartholomew, J. K. Furdyna, and A. K. Ramdas, “INTERBAND FARADAY-ROTATION IN DILUTED MAGNETIC SEMICONDUCTORS – ZN1-XMNXTE AND CD1-XMNXTE,” Physical Review B, Article vol. 34, no. 10, pp. 6943-6950, Nov 1986, doi: 10.1103/PhysRevB.34.6943.

[6] A. K. Ramdas and S. Rodriguez, “SPECTROSCOPY OF THE SOLID-STATE ANALOGS OF THE HYDROGEN-ATOM – DONORS AND ACCEPTORS IN SEMICONDUCTORS,” Reports on Progress in Physics, Review vol. 44, no. 12, pp. 1297-1387, 1981, doi: 10.1088/0034-4885/44/12/002

[7] G. Chen, I. Miotkowski, S. Rodriguez, and A. K. Ramdas, “Stoichiometry driven impurity configurations in compound semiconductors,” Physical Review Letters, Article vol. 96, no. 3, Jan 2006, Art no. 035508, doi: 10.1103/PhysRevLett.96.035508.

[8] G. Chen, J. S. Bhosale, I. Miotkowski, and A. K. Ramdas, “Spectroscopic Signatures of Novel Oxygen-Defect Complexes in Stoichiometrically Controlled CdSe,” Physical Review Letters, Article vol. 101, no. 19, Nov 2008, Art no. 195502, doi: 10.1103/PhysRevLett.101.195502.

Other Notable Papers:

[9] E. S. Oh, R. G. Alonso, I. Miotkowski, and A. K. Ramdas, “RAMAN-SCATTERING FROM VIBRATIONAL AND ELECTRONIC EXCITATIONS IN A II-VI QUATERNARY COMPOUND – CD1-X-YZNXMNYTE,” Physical Review B, Article vol. 45, no. 19, pp. 10934-10941, May 1992, doi: 10.1103/PhysRevB.45.10934.

[10] R. Vogelgesang, A. K. Ramdas, S. Rodriguez, M. Grimsditch, and T. R. Anthony, “Brillouin and Raman scattering in natural and isotopically controlled diamond,” Physical Review B, Article vol. 54, no. 6, pp. 3989-3999, Aug 1996, doi: 10.1103/PhysRevB.54.3989.

[11] M. H. Grimsditch and A. K. Ramdas, “BRILLOUIN-SCATTERING IN DIAMOND,” Physical Review B, Article vol. 11, no. 8, pp. 3139-3148, 1975, doi: 10.1103/PhysRevB.11.3139.

[12] E. S. Zouboulis, M. Grimsditch, A. K. Ramdas, and S. Rodriguez, “Temperature dependence of the elastic moduli of diamond: A Brillouin-scattering study,” Physical Review B, Article vol. 57, no. 5, pp. 2889-2896, Feb 1998, doi: 10.1103/PhysRevB.57.2889.

[13] A. K. Ramdas, S. Rodriguez, M. Grimsditch, T. R. Anthony, and W. F. Banholzer, “EFFECT OF ISOTOPIC CONSTITUTION OF DIAMOND ON ITS ELASTIC-CONSTANTS – C-13 DIAMOND, THE HARDEST KNOWN MATERIAL,” Physical Review Letters, Article vol. 71, no. 1, pp. 189-192, Jul 1993, doi: 10.1103/PhysRevLett.71.189.

.