Tag / Klein-Gordon Equation

by David D. Nolte

The Ubiquitous George Uhlenbeck

There are sometimes individuals who seem always to find themselves at the focal points of their times.  The physicist George Uhlenbeck was one of these individuals, showing up at all the right times in all the right places at the dawn of modern physics in the 1920’s and 1930’s. He studied under Ehrenfest and Bohr and Born, and he was friends with Fermi and Oppenheimer and Oskar Klein.  He taught physics at the universities at Leiden, Michigan, Utrecht, Columbia, MIT and Rockefeller.  He was a wide-ranging theoretical physicist who worked on Brownian motion, early string theory, quantum tunneling, and the master equation.  Yet he is most famous for the very first thing he did as a graduate student—the discovery of the quantum spin of the electron.

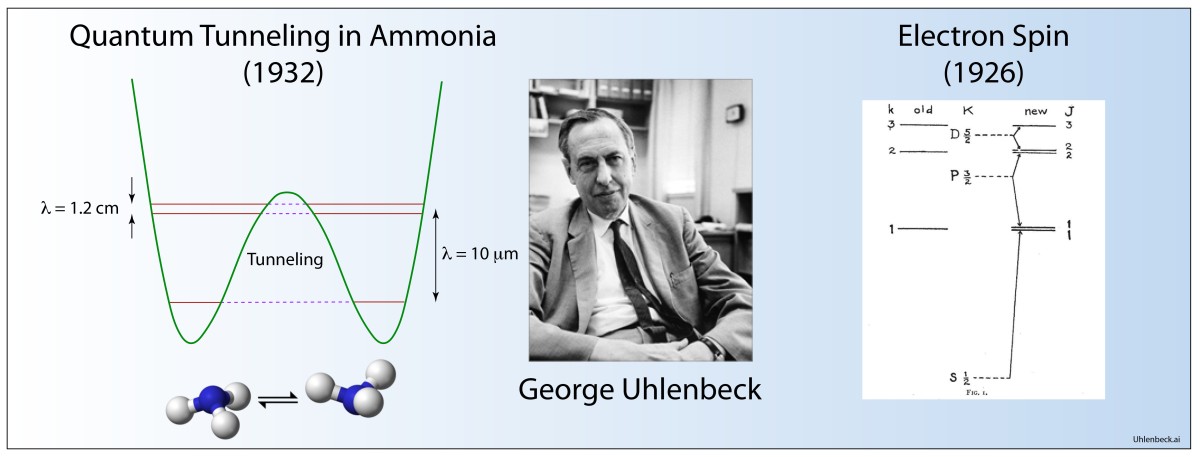
Electron Spin

G. E. Uhlenbeck, and S. Goudsmit, “Spinning electrons and the structure of spectra,” Nature 117, 264-265 (1926).

George Uhlenbeck (1900 – 1988) was born in the Dutch East Indies, the son of a family with a long history in the Dutch military [1].  After the father retired to The Hague, George was expected to follow the family tradition into the military, but he stumbled onto a copy of H. Lorentz’ introductory physics textbook and was hooked.  Unfortunately, to attend university in the Netherlands at that time required knowledge of Greek and Latin, which he lacked, so he entered the Institute of Technology in Delft to study chemical engineering.  He found the courses dreary. 

Fortunately, he was only a few months into his first semester when the language requirement was dropped, and he immediately transferred to the University of Leiden to study physics.  He tried to read Boltzmann, but found him opaque, but then read the famous encyclopedia article by the husband and wife team of Paul and Tatiana Ehrenfest on statistical mechanics (see my Physics Today article [2]), which became his lifelong focus.

After graduating, he continued into graduate school, taking classes from Ehrenfest, but lacking funds, he supported himself by teaching classes at a girls high school, until he heard of a job tutoring the son of the Dutch ambassador to Italy.  He was off to Rome for three years, where he met Enrico Fermi and took classes from Tullio Bevi-Cevita and Vito Volterra.

However, he nearly lost his way.  Surrounded by the rich cultural treasures of Rome, he became deeply interested in art and was seriously considering giving up physics and pursuing a degree in art history.  When Ehrenfest got wind of this change in heart, he recalled Uhlenbeck in 1925 to the Netherlands and shrewdly paired him up with another graduate student, Samuel Goudsmit, to work on a new idea proposed by Wolfgang Pauli a few months earlier on the exclusion principle.

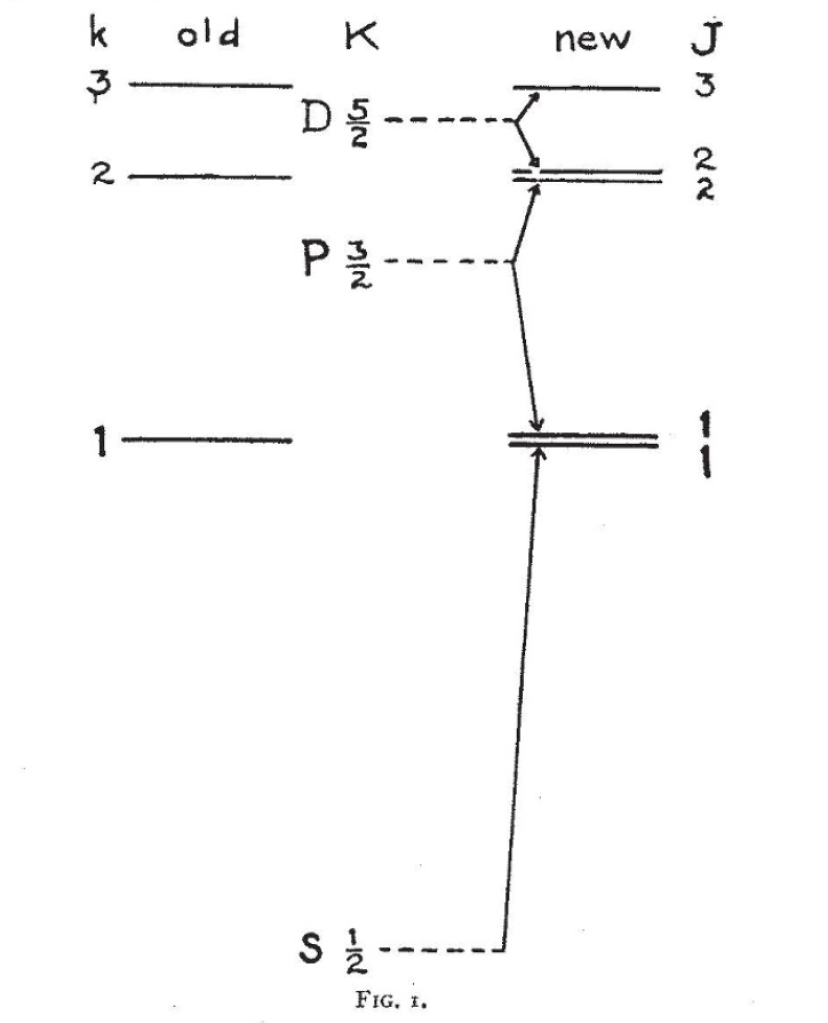
Pauli had explained the filling of the energy levels of atoms by introducing a new quantum number that had two values.  Once an energy level was filled by two electrons, each carrying one of the two quantum numbers, this energy level “excluded” any further filling by other electrons. 

To Uhlenbeck, these two quantum numbers seemed as if they must arise from some internal degree of freedom, and in a flash of insight he imagined that it might be caused if the electron were spinning.  Since spin was a form of angular momentum, the spin degree of freedom would combine with orbital angular momentum to produce a composite angular momentum for the quantum levels of atoms.

The idea of electron spin was not immediately embraced by the broader community, and Bohr and Heisenberg and Pauli had their reservations.  Fortunately, they all were traveling together to attend the 50th anniversary of Lorentz’ doctoral examination and were met at the train station in Leiden by Ehrenfest and Einstein.  As usual, Einstein had grasped the essence of the new physics and explained how the moving electron feels an induced magnetic field which would act on the magnetic moment of the electron to produce spin-orbit coupling.  With that, Bohr was convinced.

Uhlenbeck and Goudsmit wrote up their theory in a short article in Nature, followed by a short note by Bohr.  A few months later, L. H. Thomas, while visiting Bohr in Copenhagen, explained the factor of two that appears in (what later came to be called) Thomas precession of the electron, cementing the theory of electron spin in the new quantum mechanics.

5-Dimensional Quantum Mechanics

P. Ehrenfest, and G. E. Uhlenbeck, “Graphical illustration of De Broglie’s phase waves in the five-dimensional world of O Klein,” Zeitschrift Fur Physik 39, 495-498 (1926).

Around this time, the Swedish physicist Oskar Klein visited Leiden after returning from three years at the University of Michigan where he had taken advantage of the isolation to develop a quantum theory of 5-dimensional spacetime.  This was one of the first steps towards a grand unification of the forces of nature since there was initial hope that gravity and electromagnetism might both be expressed in terms of the five-dimensional space.

An unusual feature of Klein’s 5-dimensional relativity theory was the compactness of the fifth dimension, in which it was “rolled up” into a kind of high-dimensional string with a tiny radius.  If the 4-dimensional theory of spacetime was sometimes hard to visualize, here was an even tougher problem.

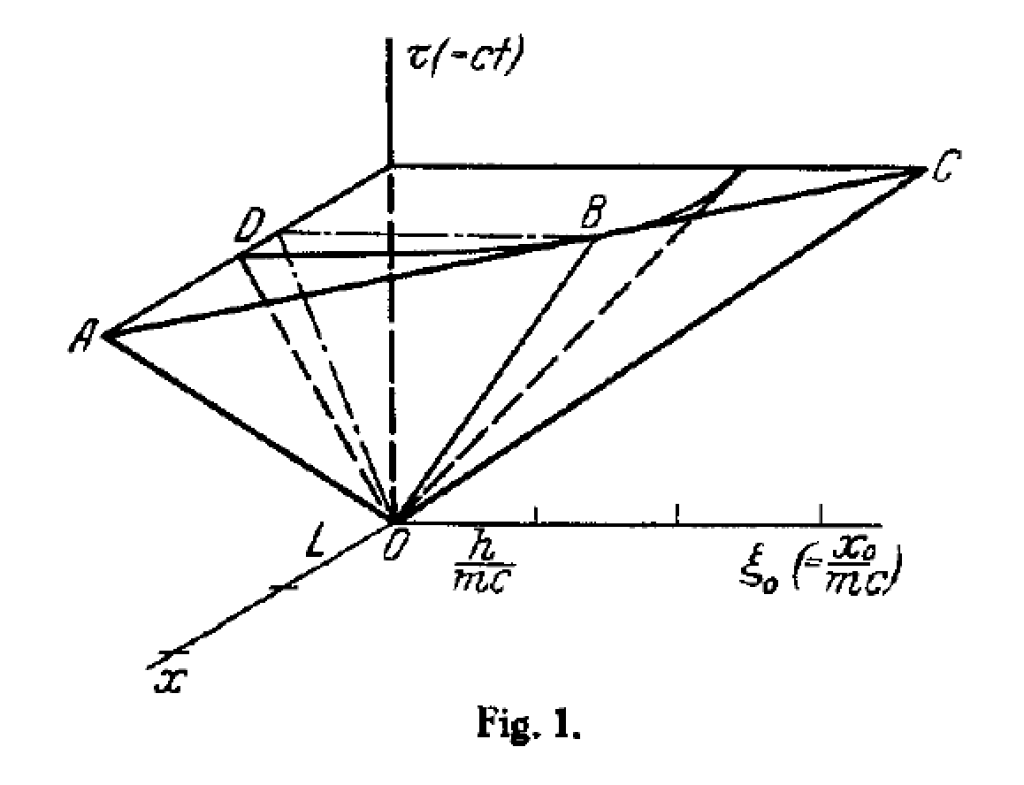
Uhlenbeck and Ehrenfest met often with Klein during his stay in Leiden, discussing the geometry and consequences of the 5-dimensional theory.  Ehrenfest was always trying to get at the essence of physical phenomena in the simplest terms.  His famous refrain was “Was ist der Witz?” (What is the point?) [1].  These discussions led to a simple paper in Zeitschrift für Physik published later that year in 1926 by Ehrenfest and Uhlenbeck with the compelling title “Graphical Illustration of De Broglie’s Phase Waves in the Five-Dimensional World of O Klein”.  The paper provided the first visualization of the 5-dimensional spacetime with the compact dimension.  The string-like character of the spacetime was one of the first forays into modern day “string theory” whose dimensions have now expanded to 11 from 5.

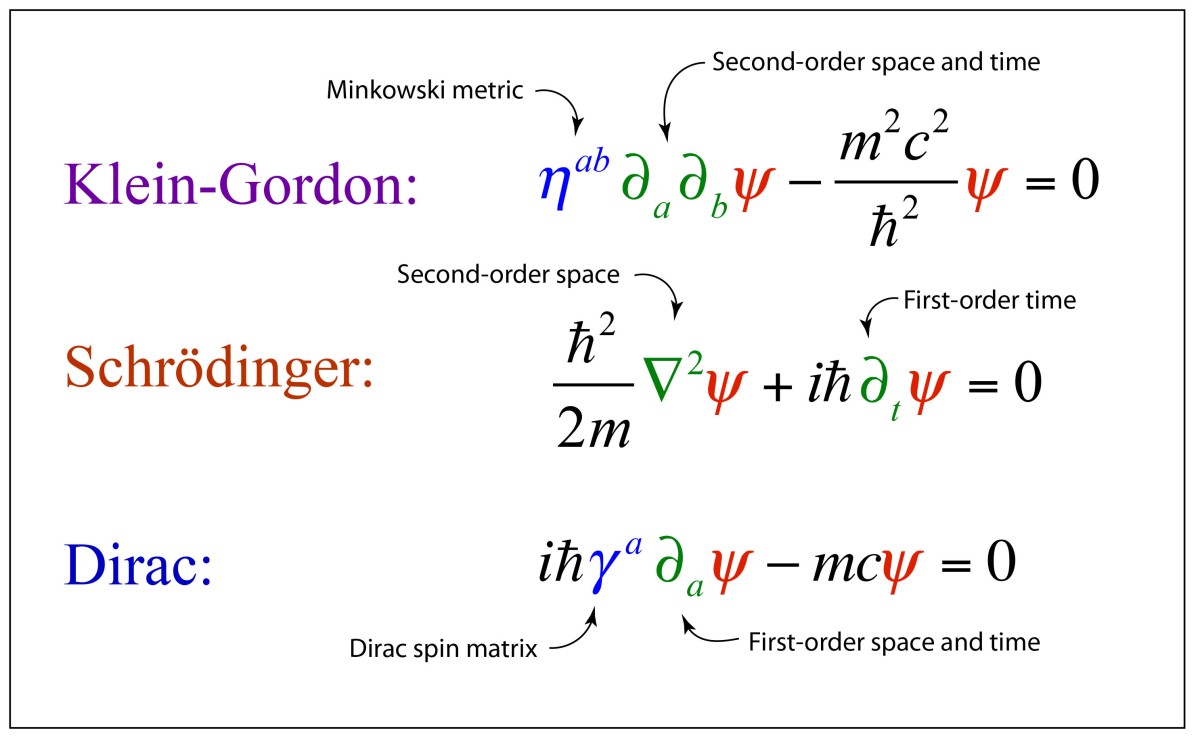
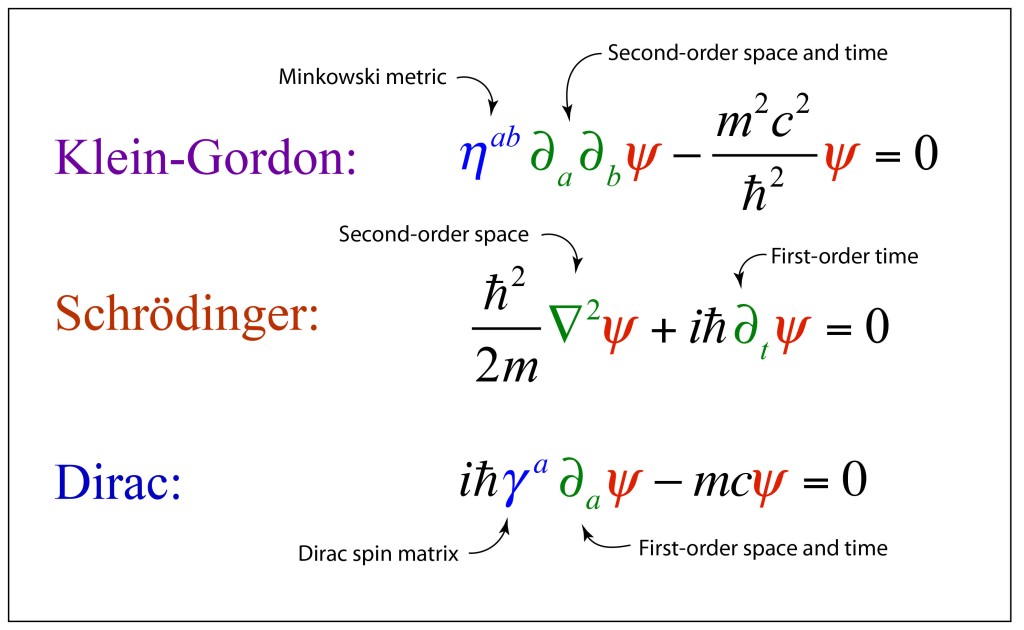
During his visit, Klein also told Uhlenbeck about the relativistic Schrödinger equation that he was working on, which would later become the Klein-Gordon equation.  This was a near miss, because what the Klein-Gordon equation was missing was electron spin—which Uhlenbeck himself had introduced into quantum theory—but it would take a few more years before Dirac showed how to incorporate spin into the theory.

Brownian Motion

G. E. Uhlenbeck and L. S. Ornstein, “On the theory of the Brownian motion,” Physical Review 36, 0823-0841 (1930).

After spending time with Bohr in Copenhagen while finishing his PhD, Uhlenbeck visited Max Born at Göttingen where he met J. Robert Oppenheimer who was also visiting Born at that time.  When Uhlenbeck traveled to the United States in late summer of 1927 to take a position at the University of Michigan, he was met at the dock in New York by Oppenheimer.

Uhlenbeck was a professor of physics at Michigan for eight years from 1927 to 1935, and he instituted a series of Summer Schools [3] in theoretical physics that attracted international participants and introduced a new generation of American physicists to the rigors of theory that they previously had to go to Europe to find. 

In this way, Uhlenbeck was part of a great shift that occurred in the teaching of graduate-level physics of the 1930’s that brought European expertise to the United States.  Just a decade earlier, Oppenheimer had to go to Göttingen to find the kind of education that he needed for graduate studies in physics.  Oppenheimer brought the new methods back with him to Berkeley, where he established a strong theory department to match the strong experimental activities of E. O. Lawrence.  Now, European physicists too were coming to America, an exodus accelerated by the increasing anti-Semitism in Europe under the rise of fascism. 

During this time, one of Uhlenbeck’s collaborators was L. S. Ornstein, the director of the Physical Laboratory at the University of Utrecht and a founding member of the Dutch Physical Society.  Uhlenbeck and Ornstein were both interested in the physics of Brownian motion, but wished to establish the phenomenon on a more sound physical basis.  Einstein’s famous paper of 1905 on Brownian motion had made several Einstein-style simplifications that stripped the complicated theory to its bare essentials, but had lost some of the details in the process, such as the role of inertia at the microscale.

Uhlenbeck and Ornstein published a paper in 1930 that developed the stochastic theory of Brownian motion, including the effects of particle inertia. The stochastic differential equation (SDE) for velocity is

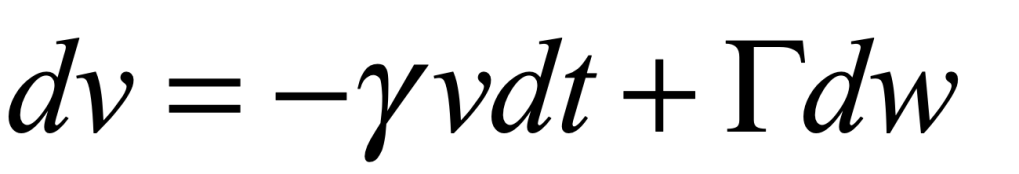
where γ is viscosity, Γ is a fluctuation coefficient, and dw is a “Wiener process”. The Wiener differential dw has unusual properties such that

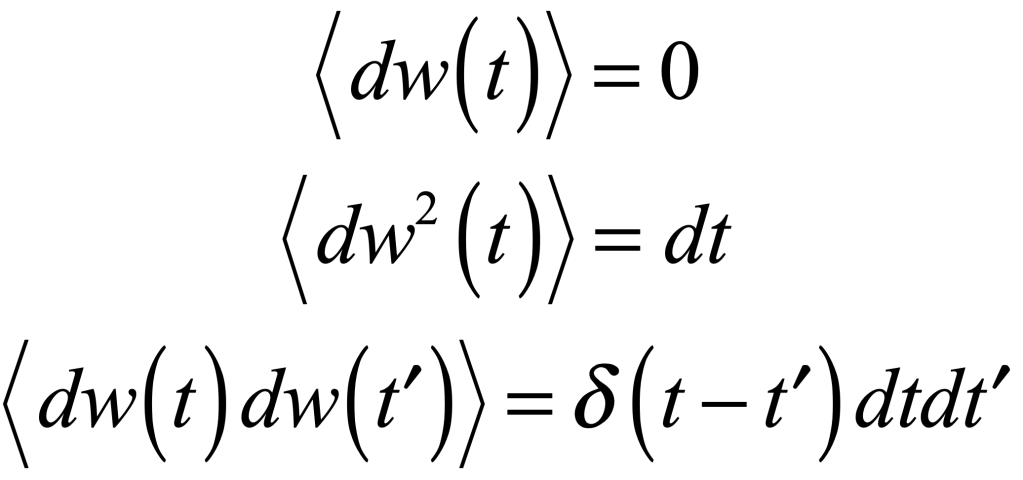
Uhlenbeck and Ornstein solived this SDE to yield an average velocity

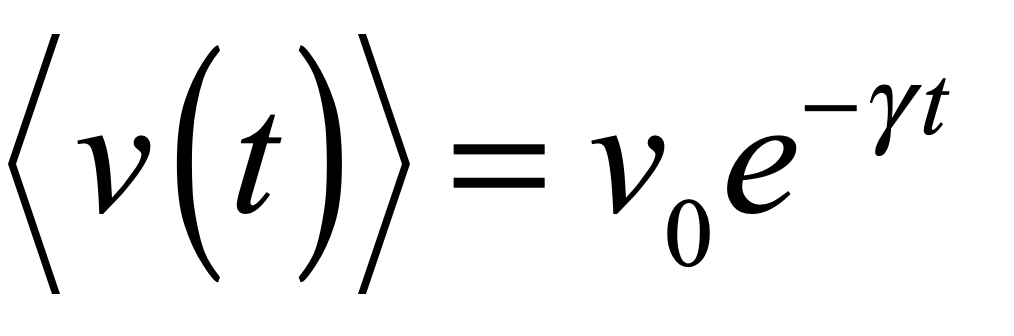
which decays to zero at long times, and a variance

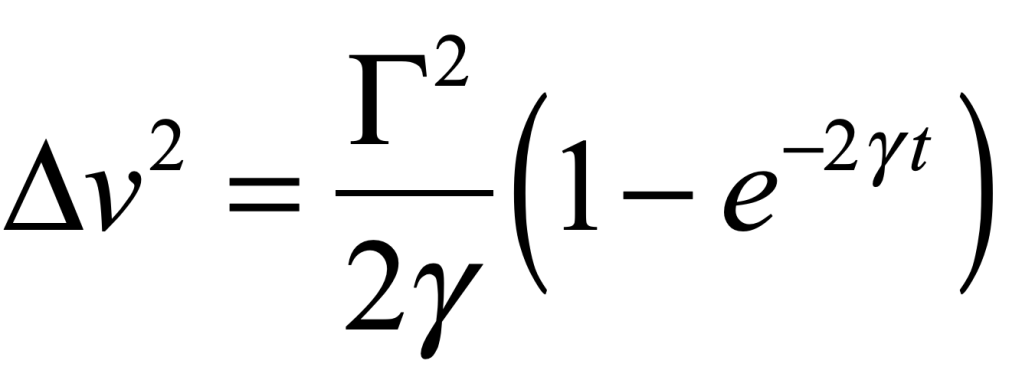
that asymptotes to a finite value at long times. The fluctuation coefficient is thus given by

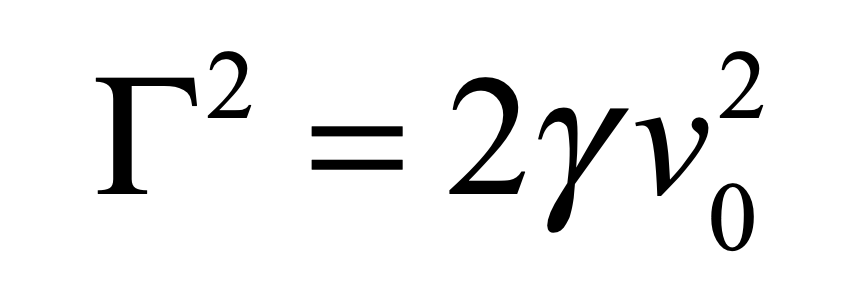
for a process with characteristic speed v0. An estimate for the fluctuation coefficient can be obtained by considering the force F on an object of size a

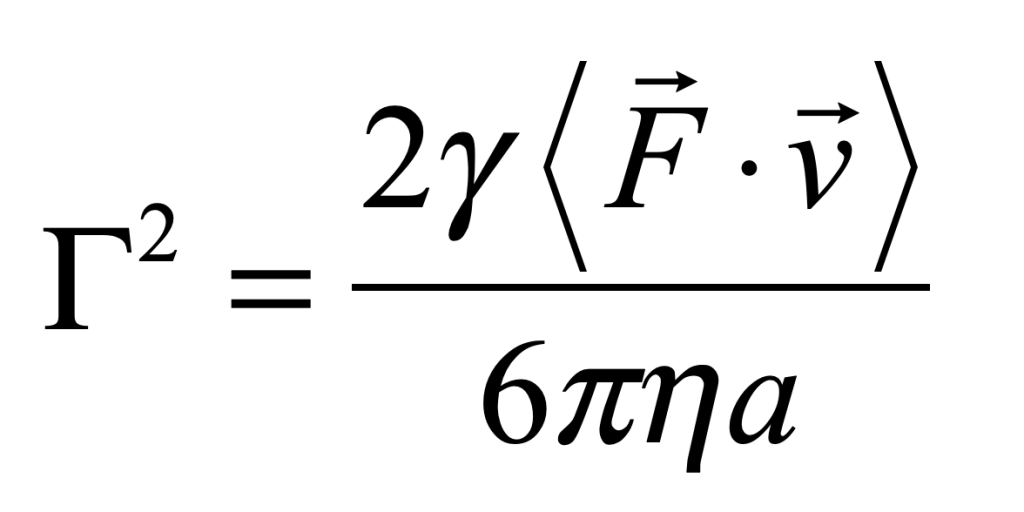
For instance, for intracellular transport [4], the fluctuation coefficient has a rough value of Γ = 2 Hz μm2/sec2.

Quantum Tunneling

D. M. Dennison and G. E. Uhlenbeck, “The two-minima problem and the ammonia molecule,” Physical Review 41, 313-321 (1932).

By the early 1930’s, quantum tunnelling of the electron through classically forbidden regions of potential energy was well established, but electrons did not have a monopoly on quantum effects.  Entire atoms—electrons plus nucleus—also have quantum wave functions and can experience regions of classically forbidden potential.

Uhlenbeck, with David Dennison, a fellow physicist at Ann Arbor, Michigan, developed the first quantum theory of molecular tunneling for the molecular configuration of ammonia NH3 that can tunnel between the two equivalent configurations. Their use of the WKB approximation in the paper set the standard for subsequent WKB approaches that would play an important role in the calculation of nuclear decay rates.

Master Equation

A. Nordsieck, W. E. Lamb, and G. E. Uhlenbeck, “On the theory of cosmic-ray showers I. The furry model and the fluctuation problem,” Physica 7, 344-360 (1940)

In 1935, Uhlenbeck left Michigan to take up the physics chair recently vacated by Kramers at Utrecht.  However, watching the rising Nazism in Europe, he decided to return to the United States, beginning as a visiting professor at Columbia University in New York in 1940.  During his visit, he worked with W. E. Lamb and A. Nordsieck on the problem of cosmic ray showers. 

Their publication on the topic included a rate equation that is encountered in a wide range of physical phenomena. They called it the “Master Equation” for ease of reference in later parts of the paper, but this phrase stuck, and the “Master Equation” is now a standard tool used by physicists when considering the balances among multiples transitions.

Uhlenbeck never returned to Europe, moving among Michigan, MIT, Princeton and finally settling at Rockefeller University in New York from where he retired in 1971.

Selected Works by George Uhlenbeck:

G. E. Uhlenbeck, and S. Goudsmit, “Spinning electrons and the structure of spectra,” Nature 117, 264-265 (1926).

P. Ehrenfest, and G. E. Uhlenbeck, “On the connection of different methods of solution of the wave equation in multi dimensional spaces,” Proceedings of the Koninklijke Akademie Van Wetenschappen Te Amsterdam 29, 1280-1285 (1926).

P. Ehrenfest, and G. E. Uhlenbeck, “Graphical illustration of De Broglie’s phase waves in the five-dimensional world of O Klein,” Zeitschrift Fur Physik 39, 495-498 (1926).

G. E. Uhlenbeck, and L. S. Ornstein, “On the theory of the Brownian motion,” Physical Review 36, 0823-0841 (1930).

D. M. Dennison, and G. E. Uhlenbeck, “The two-minima problem and the ammonia molecule,” Physical Review 41, 313-321 (1932).

E. Fermi, and G. E. Uhlenbeck, “On the recombination of electrons and positrons,” Physical Review 44, 0510-0511 (1933).

A. Nordsieck, W. E. Lamb, and G. E. Uhlenbeck, “On the theory of cosmic-ray showers I The furry model and the fluctuation problem,” Physica 7, 344-360 (1940).

M. C. Wang, and G. E. Uhlenbeck, “On the Theory of the Brownian Motion-II,” Reviews of Modern Physics 17, 323-342 (1945).

G. E. Uhlenbeck, “50 Years of Spin – Personal Reminiscences,” Physics Today 29, 43-48 (1976).

Notes:

[1] George Eugene Uhlenbeck: A Biographical Memoire by George Ford (National Academy of Sciences, 2009). https://www.nasonline.org/publications/biographical-memoirs/memoir-pdfs/uhlenbeck-george.pdf

[2] D. D. Nolte, “The tangled tale of phase space,” Physics Today 63, 33-38 (2010).

NoltePT10Download

[3] One of these was the famous 1948 Summer School session where Freeman Dyson met Julian Schwinger after spending days on a cross-country road trip with Richard Feynman. Schwinger and Feynman had developed two different approaches to quantum electrodynamics (QED), which Dyson subsequently reconciled when he took up his position later that year at Princeton’s Institute for Advanced Study, helping to launch the wave of QED that spread out over the theoretical physics community.

[4] D. D. Nolte, “Coherent light scattering from cellular dynamics in living tissues,” Reports on Progress in Physics 87 (2024).

by David D. Nolte

The Many Dimensions of Oskar Klein

The idea of parallel dimensions in physics has a long history dating back to Bernhard Riemann’s famous 1954 lecture on the foundations of geometry that he gave as a requirement to attain a teaching position at the University of Göttingen.  Riemann laid out a program of study that included physics problems solved in multiple dimensions, but it was Rudolph Lipschitz twenty years later who first composed a rigorous view of physics as trajectories in many dimensions.  Nonetheless, the three spatial dimensions we enjoy in our daily lives remained the only true physical space until Hermann Minkowski re-expressed Einstein’s theory of relativity in 4-dimensional space time.  Even so, Minkowski’s time dimension was not on an equal footing with the three spatial dimensions—the four dimensions were entwined, but time had a different characteristic, what is known as pseudo-Riemannian metric.  It is this pseudo-metric that allows space-time distances to be negative as easily as positive.

In 1919 Theodore Kaluza of the University of Königsberg in Prussia extended Einstein’s theory of gravitation to a fifth spatial dimension, and physics had its first true parallel dimension.  It was more than just an exercise in mathematics—adding a fifth dimension to relativistic dynamics adds new degrees of freedom that allow the dynamical 5-dimensional theory to include more than merely relativistic massive particles and the electric field they generate.  In addition to electro-magnetism, something akin to Einstein’s field equation of gravitation emerges.  Here was a five-dimensional theory that seemed to unify E&M with gravity—a first unified theory of physics.  Einstein, to whom Kaluza communicated his theory, was intrigued but hesitant to forward Kaluza’s paper for publication.  It seemed too good to be true.  But Einstein finally sent it to be published in the proceedings of the Prussian Academy of Sciences [Kaluza, 1921]. He later launched his own effort to explore such unified field theories more deeply.

Yet Kaluza’s theory was fully classical—if a fifth dimension can be called that—because it made no connection to the rapidly developing field of quantum mechanics. The person who took the step to make five-dimensional space-time into a quantum field theory was Oskar Klein.

Oskar Klein (1894 – 1977)

Oskar Klein was a Swedish physicist who was in the “second wave” of quantum physicists just a few years behind the titans Heisenberg and Schrödinger and Pauli.  He began as a student in physical chemistry working in Stockholm under the famous Arrhenius.  It was arranged for him to work in France and Germany in 1914, but he was caught in Paris at the onset of World War I.  Returning to Sweden, he enlisted in military service from 1915 to 1916 and then joined Arrhenius’ group at the Nobel Institute where he met Hendrick Kramers—Bohr’s direct assistant at Copenhagen at that time.  At Kramer’s invitation, Klein traveled to Copenhagen and worked for a year with Kramers and Bohr before returning to defend his doctoral thesis in 1921 in the field of physical chemistry.  Klein’s work with Bohr had opened his eyes to the possibilities of quantum theory, and he shifted his research interest away from physical chemistry.  Unfortunately, there were no positions at that time in such a new field, so Klein accepted a position as assistant professor at the University of Michigan in Ann Arbor where he stayed from 1923 to 1925. 

Oskar Klein in the late 1920’s

The Fifth Dimension

In an odd twist of fate, this isolation of Klein from the mainstream quantum theory being pursued in Europe freed him of the bandwagon effect and allowed him to range freely on topics of his own devising and certainly in directions all his own.  Unaware of Kaluza’s previous work, Klein expanded Minkowski’s space-time from four to five spatial dimensions, just as Kaluza had done, but now with a quantum interpretation.  This was not just an incremental step but had far-ranging consequences in the history of physics.

Klein found a way to keep the fifth dimension Euclidean in its metric properties while rolling itself up compactly into a cylinder with the radius of the Planck length—something inconceivably small.  This compact fifth dimension made the manifold into something akin to an infinitesimal string.  He published a short note in Nature magazine in 1926 on the possibility of identifying the electric charge within the 5-dimensional theory [Klein, 2916a]. He then returned to Sweden to take up a position at the University of Lund.  This odd string-like feature of 5-dimensional space-time was picked up by Einstein and others in their search for unified field theories of physics, but the topic soon drifted from the lime light where it lay dormant for nearly fifty years until the first forays were made into string theory. String theory resurrected the Kaluza-Klein theory which has bourgeoned into the vast topic of String Theory today, including Superstrings that occur in 10+1 dimensions at the frontiers of physics. 

Dirac Electrons without the Spin: Klein-Gordon Equation

Once back in Europe, Klein reengaged with the mainstream trends in the rapidly developing quantum theory and in 1926 developed a relativistic quantum theory of the electron [Klein, 1926b].  Around the same time Walter Gordon also proposed this equation, which is now called the “Klein-Gordon Equation”.  The equation was a classic wave equation that was second order in both space and time.  This was the most natural form for a wave equation for quantum particles and Schrödinger himself had started with this form.  But Schrödinger had quickly realized that the second-order time term in the equation did not capture the correct structure of the hydrogen atom, which led him to express the time-dependent term in first order and non-relativistically—which is today’s “Schrödinger Equation”.  The problem was in the spin of the electron.  The electron is a spin-1/2 particle, a Fermion, which has special transformation properties.  It was Dirac a few years later who discovered how to express the relativistic wave equation for the electron—not by promoting the time-dependent term to second order, but by demoting the space-dependent term to first order.  The first-order expression for both the space and time derivatives goes hand in hand with the Pauli spin matrices for the electron, and the Dirac Equation is the appropriate relativistically-correct wave equation for the electron.

Klein’s relativistic quantum wave equation does turn out to be the relevant form for a spin-less particle like the pion, but the pion decays by the strong nuclear force and the Klein-Gordon equation is not a practical description.  However, the Higgs boson also is a spin-zero particle, and the Klein-Gordon expression does have relevance for this fundamental exchange particle.

Klein Tunneling

In those early days of the late 1920’s, the nature of the nucleus was still a mystery, especially the problem of nuclear radioactivity where a neutron could convert to a proton with the emission of an electron.  Some suggested that the neutron was somehow a proton that had captured an electron in a potential barrier.  Klein showed that this was impossible, that the electrons would be highly relativistic—something known as a Dirac electron—and they would tunnel with perfect probability through any potential barrier [Klein, 1929].  Therefore, Klein concluded, no nucleon or nucleus could bind an electron. 

This phenomenon of unity transmission through a barrier became known as Klein tunneling. The relativistic electron transmits perfectly through an arbitrary potential barrier—independent of its width or height. This is unlike light that transmits through a dielectric slab in resonances that depend on the thickness of the slab—also known as a Fabry-Perot interferometer. The Dirac electron can have any energy, and the potential barrier can have any width, yet the electron will tunnel with 100% probability. How can this happen?

The answer has to do with the dispersion (velocity versus momentum) of the Dirac electron. As the momentum changes in a potential the speed of the Dirac electron stays constant. In the potential barrier, the moment flips sign, but the speed remains unchanged. This is equivalent to the effects of negative refractive index in optics. If a photon travels through a material with negative refractive index, its momentum is flipped, but its speed remains unchanged. From Fermat’s principle, it is speed which determines how a particle like a photon refracts, so if there is no speed change, then there is no reflection.

For the case of Dirac electrons in a potential with field F, speed v and transverse momentum py, the transmission coefficient is given by

If the transverse momentum is zero, then the transmission is perfect. A visual schematic of the role of dispersion and potentials for Dirac electrons undergoing Klein tunneling is shown in the next figure.

Dispersion of Dirac electrons at a potential step. Reprinted from https://www.arxiv-vanity.com/papers/0710.3848/

In this case, even if the transverse momentum is not strictly zero, there can still be perfect transmission. It is simply a matter of matching speeds.

Graphene became famous over the past decade because its electron dispersion relation is just like a relativistic Dirac electron with a Dirac point between conduction and valence bands. Evidence for Klein tunneling in graphene systems has been growing, but clean demonstrations have remained difficult to observe.

Now, published in the Dec. 2020 issue of Science magazine—almost a century after Klein first proposed it—an experimental group at the University of California at Berkeley reports a beautiful experimental demonstration of Klein tunneling—not from a nucleus, but in an acoustic honeycomb sounding board the size of a small table—making an experimental analogy between acoustics and Dirac electrons that bears out Klein’s theory.

The accoustic Klein tunneling sounding board at Berkeley. Reprinted from https://science.sciencemag.org/content/370/6523/1447

In this special sounding board, it is not electrons but phonons—acoustic vibrations—that have a Dirac point. Furthermore, by changing the honeycomb pattern, the bands can be shifted, just like in a p-n-p junction, to produce a potential barrier. The Berkeley group, led by Xiang Zhang (now president of Hong Kong University), fabricated the sounding board that is about a half-meter in length, and demonstrated dramatic Klein tunneling.

It is amazing how long it can take between the time a theory is first proposed and the time a clean experimental demonstration is first performed.  Nearly 90 years has elapsed since Klein first derived the phenomenon. Performing the experiment with actual relativistic electrons was prohibitive, but bringing the Dirac electron analog into the solid state has allowed the effect to be demonstrated easily.

References

[1921] Kaluza, Theodor (1921). “Zum Unitätsproblem in der Physik”. Sitzungsber. Preuss. Akad. Wiss. Berlin. (Math. Phys.): 966–972

[1926a] Klein, O. (1926). “The Atomicity of Electricity as a Quantum Theory Law”. Nature 118: 516-516.

[1926b] Klein, O. (1926). “Quantentheorie und fünfdimensionale Relativitätstheorie”. Zeitschrift für Physik. 37 (12): 895

[1929] Klein, O. (1929). “Die Reflexion von Elektronen an einem Potentialsprung nach der relativistischen Dynamik von Dirac”. Zeitschrift für Physik. 53 (3–4): 157