When Leibniz claimed in 1704, in a published article in Acta Eruditorum, to have invented the differential calculus in 1684 prior to anyone else, the British mathematicians rushed to Newton’s defense. They knew Newton had developed his fluxions as early as 1666 and certainly no later than 1676. Thus ensued one of the most bitter and partisan priority disputes in the history of math and science that pitted the continental Leibnizians against the insular Newtonians. Although a (partisan) committee of the Royal Society investigated the case and found in favor of Newton, the affair had the effect of insulating British mathematics from Continental mathematics, creating an intellectual desert as the forefront of mathematical analysis shifted to France. Only when George Green filled his empty hours with the latest advances in French analysis, as he tended his father’s grist mill, did British mathematics wake up. Green self-published his epic work in 1828 that introduced what is today called Green’s Theorem.
Yet the period from 1700 to 1828 was not a complete void for British mathematics. A few points of light shone out in the darkness, Thomas Simpson, Collin Maclaurin, Abraham de Moivre, and Brook Taylor (1685 – 1731) who came from an English family that had been elevated to minor nobility by an act of Cromwell during the English Civil War.
Growing up in Bifrons House

When Brook Taylor was ten years old, his father bought Bifrons House [1], one of the great English country houses, located in the county of Kent just a mile south of Canterbury. English country houses were major cultural centers and sources of employment for 300 years from the seventeenth century through the early 20th century. While usually being the country homes of nobility of all levels, from Barons to Dukes, sometimes they were owned by wealthy families or by representatives in Parliament, which was the case for the Taylors. Bifrons House had been built around 1610 in the Jacobean architectural style that was popular during the reign of James I. The house had a stately front façade, with cupola-topped square towers, gable ends to the roof, porches of a renaissance form, and extensive manicured gardens on the south side. Bifrons House remained the seat of the Taylor family until 1824 when they moved to a larger house nearby and let Bifrons first to a Marquess and then in 1828 to Lady Byron (ex-wife of Lord Byron) and her daughter Ada Lovelace (the mathematician famous for her contributions to early computer science). The Taylor’s sold the house in 1830 to the first Marquess Conyngham.
Taylor’s life growing up in the rarified environment of Bifrons House must have been like scenes out of the popular BBC TV drama Downton Abbey. The house had a large staff of servants and large grounds at the edge of a large park near the town of Patrixbourne. Life as the heir to the estate would have been filled with social events and fine arts that included music and painting. Taylor developed a life-long love of music during his childhood, later collaborating with Isaac Newton on a scientific investigation of music (it was never published). He was also an amateur artist, and one of the first books he published after being elected to the Royal Society was on the mathematics of linear perspective, which contained some of the early results of projective geometry.
There is a beautiful family portrait in the National Portrait Gallery in London painted by John Closterman around 1696. The portrait is of the children of John Taylor about a year after he purchased Bifrons House. The painting is notable because Brook, the heir to the family fortunes, is being crowned with a wreath by his two older sisters (who would not inherit). Brook was only about 11 years old at the time and was already famous within his family for his ability with music and numbers.

Taylor never had to go to school, being completely tutored at home until he entered St. John’s College, Cambridge, in 1701. He took mathematics classes from Machin and Keill and graduated in 1709. The allowance from his father was sufficient to allow him to lead the life of a gentleman scholar, and he was elected a member of the Royal Society in 1712 and elected secretary of the Society just two years later. During the following years he was active as a rising mathematician until 1721 when he married a woman of a good family but of no wealth. The support of a house like Bifrons always took money, and the new wife’s lack of it was enough for Taylor’s father to throw the new couple out. Unfortunately, his wife died in childbirth along with the child, so Taylor returned home in 1723. These family troubles ended his main years of productivity as a mathematician.

Methodus incrementorum directa et inversa
Under the eye of the Newtonian mathematician Keill at Cambridge, Taylor became a staunch supporter and user of Newton’s fluxions. Just after he was elected as a member of the Royal Society in 1712, he participated in an investigation of the priority for the invention of the calculus that pitted the British Newtonians against the Continental Leibnizians. The Royal Society found in favor of Newton (obviously) and raised the possibility that Leibniz learned of Newton’s ideas during a visit to England just a few years before Leibniz developed his own version of the differential calculus.
A re-evaluation of the priority dispute from today’s perspective attributes the calculus to both men. Newton clearly developed it first, but did not publish until much later. Leibniz published first and generated the excitement for the new method that dispersed its use widely. He also took an alternative route to the differential calculus that is demonstrably different than Newton’s. Did Leibniz benefit from possibly knowing Newton’s results (but not his methods)? Probably. But that is how science is supposed to work … building on the results of others while bringing new perspectives. Leibniz’ methods and his notations were superior to Newton’s, and the calculus we use today is closer to Leibniz’ version than to Newton’s.

Once Taylor was introduced to Newton’s fluxions, he latched on and helped push its development. The same year (1715) that he published a book on linear perspective for art, he also published a ground-breaking book on the use of the calculus to solve practical problems. This book, Methodus incrementorum directa et inversa, introduced several new ideas, including finite difference methods (which are used routinely today in numerical simulations of differential equations). It also considered possible solutions to the equation for a vibrating string for the first time.
The vibrating string is one of the simplest problem in “continuum mechanics”, but it posed a severe challenge to Newtonian physics of point particles. It was only much later that D’Alembert used Newton’s first law of action-reaction to eliminate internal forces to derive D’Alembert’s principle on the net force on an extended body. Yet Taylor used finite differences to treat the line mass of the string in a way that yielded a possible solution of a sine function. (To read about Taylor’s original contribution to the principle of superposition, see Chapter 2 of Interference.) Taylor was the first to propose that a sine function was the form of the string displacement during vibration. This idea would be taken up later by D’Alembert (who first derived the wave equation), and by Euler (who vehemently disagreed with D’Alembert’s solutions) and Daniel Bernoulli (who was the first to suggest that it is not just a single sine function, but a sum of sine functions, that described the string’s motion — the principle of superposition).
Of course, the most influential idea in Taylor’s 1715 book was his general use of an infinite series to describe a curve.
Taylor’s Series
Infinite series became a major new tool in the toolbox of analysis with the publication of John Wallis‘ Arithmetica Infinitorum published in 1656. Shortly afterwards many series were published such as Nikolaus Mercator‘s series (1668)

and James Gregory‘s series (1668)

And of course Isaac Newton’s generalized binomial theorem that he worked out famously during the plague years of 1665-1666

But these consisted mainly of special cases that had been worked out one by one. What was missing was a general method that could yield a series expression for any curve.
Taylor used concepts of finite differences as well as infinitesimals to derive his formula for expanding a function as a power series around any point. His derivation in Methodus incrementorum directa et inversa is not easily recognized today. Using difference tables, and ideas from Newton’s fluxions that viewed functions as curves traced out as a function of time, he arrived at the somewhat cryptic expression

where the “dots” are time derivatives, x stands for the ordinate (the function), v is a finite difference, and z is the abcissa moving with constant speed. If the abcissa moves with unit speed, then this becomes Taylor’s Series (in modern notation)

The term “Taylor’s series” was probably first used by L’Huillier in 1786, although Condorcet attributed the equation to both Taylor and d’Alembert in 1784. It was Lagrange in 1797 who immortalized Taylor by claiming that Taylor’s theorem was the foundation of analysis.

Example: sin(x)
Expand sin(x) around x = π

This is related to the expansion around x = 0 (also known as a Maclaurin series)

Example: arctan(x)
To get an feel for how to apply Taylor’s theorem to a function like arctan, begin with

and take the derivative of both sides

Rewrite this as

and substitute the expression for y

and integrate term by term to arrive at

This is James Gregory’s famous series. Although the math here is modern and only takes a few lines, it parallel’s Gregory’s approach. But Gregory had to invent aspects of calculus as he went along — his derivation covering many dense pages. In the priority dispute between Leibniz and Newton, Gregory is usually overlooked as an independent inventor of many aspects of the calculus. This is partly because Gregory acknowledged that Newton had invented it first, and he delayed publishing to give Newton priority.
Two-Dimensional Taylor’s Series
The ideas behind the Taylor’s series generalizes to any number of dimensions. For a scalar function of two variables it takes the form (out to second order)

where J is the Jacobian matrix (vector) and H is the Hessian matrix defined for the scalar function as

and

As a concrete example, consider the two-dimensional Gaussian function

The Jacobean and Hessian matrices are

which are the first- and second-order coefficients of the Taylor series.
References
[1] “A History of Bifrons House”, B. M. Thomas, Kent Archeological Society (2017)
[2] L. Feigenbaum, “TAYLOR,BROOK AND THE METHOD OF INCREMENTS,” Archive for History of Exact Sciences, vol. 34, no. 1-2, pp. 1-140, (1985)
[3] A. Malet, “GREGORIE, JAMES ON TANGENTS AND THE TAYLOR RULE FOR SERIES EXPANSIONS,” Archive for History of Exact Sciences, vol. 46, no. 2, pp. 97-137, (1993)
[4] E. Harier and G. Wanner, Analysis by its History (Springer, 1996)

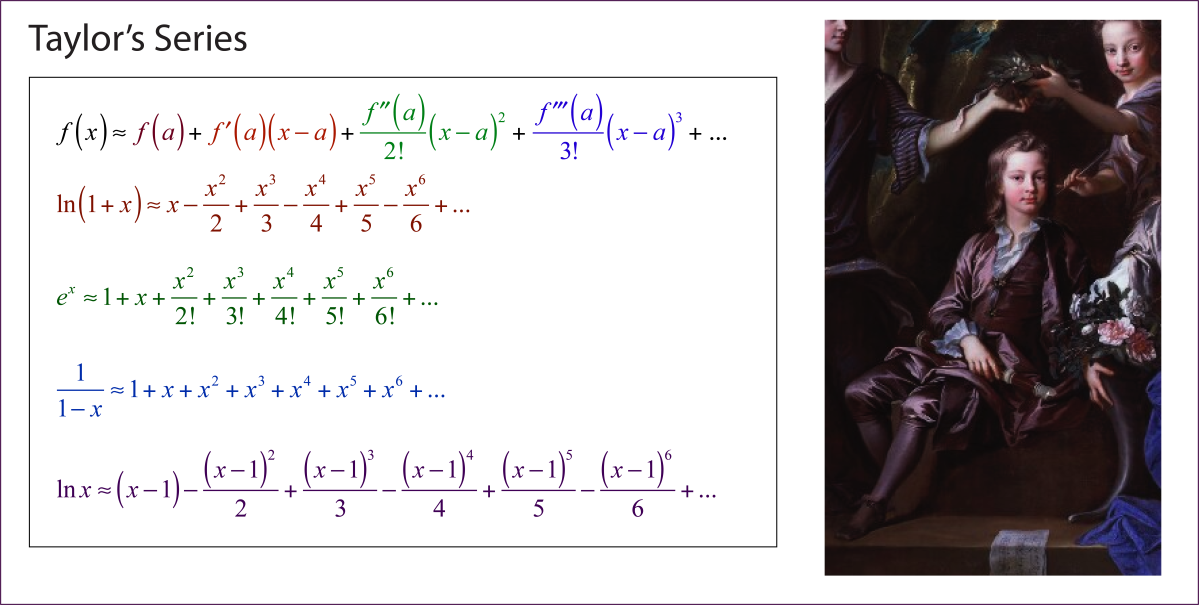
[…] Brook Taylor’s Infinite Series […]
LikeLike
[…] the Taylor’s Series (and who grew up on the opposite end of the economic spectrum from Green, see my Blog on Taylor). However, the French mathematicians in the early 1800’s were especially productive, including […]
LikeLike
[…] Brook Taylor’s Infinite Series […]
LikeLike
[…] Brook Taylor’s Infinite Series […]
LikeLike
[…] Brook Taylor’s Infinite Series […]
LikeLike
[…] https://galileo-unbound.blog/2020/08/03/brook-taylors-infinite-series/ […]
LikeLike
[…] Brook Taylor’s Infinite Series […]
LikeLike