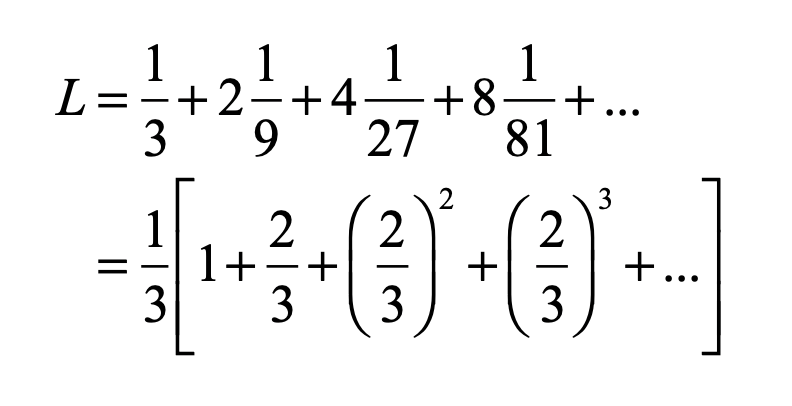Tag / Nonlinear Dynamics

Blogs on the physics of nonlinear and complex systems, including chaos theory and synchronization.

by David D. Nolte

A Short History of Chaos Theory

Chaos seems to rule our world.  Weather events, natural disasters, economic volatility, empire building—all these contribute to the complexities that buffet our lives.  It is no wonder that ancient man attributed the chaos to the gods or to the fates, infinitely far from anything we can comprehend as cause and effect.  Yet there is a balm to soothe our wounds from the slings of life—Chaos Theory—if not to solve our problems, then at least to understand them.

(Sections of this Blog have been excerpted

from the book Galileo Unbound, published by Oxford University Press)

Chaos Theory is the theory of complex systems governed by multiple factors that produce complicated outputs.  The power of the theory is its ability recognize when the complicated outputs are not “random”, no matter how complicated they are, but are in fact determined by the inputs.  Furthermore, chaos theory finds structures and patterns within the output—like the fractal structures known as “strange attractors”.  These patterns not only are not random, but they tell us about the internal mechanics of the system, and they tell us where to look “on average” for the system behavior. 

In other words, chaos theory tames the chaos, and we no longer need to blame gods or the fates.

Henri Poincare (1889)

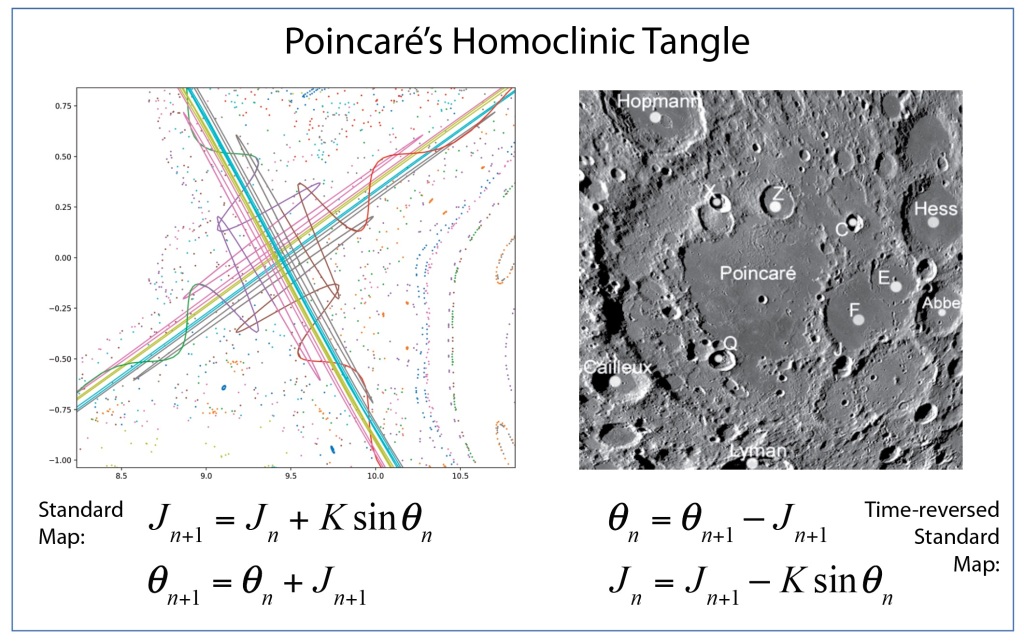
The first glimpse of the inner workings of chaos was made by accident when Henri Poincaré responded to a mathematics competition held in honor of the King of Sweden.  The challenge was to prove whether the solar system was absolutely stable, or whether there was a danger that one day the Earth would be flung from its orbit.  Poincaré had already been thinking about the stability of dynamical systems so he wrote up his solution to the challenge and sent it in, believing that he had indeed proven that the solar system was stable.

His entry to the competition was the most convincing, so he was awarded the prize and instructed to submit the manuscript for publication.  The paper was already at the printers and coming off the presses when Poincaré was asked by the competition organizer to check one last part of the proof which one of the reviewer’s had questioned relating to homoclinic orbits.

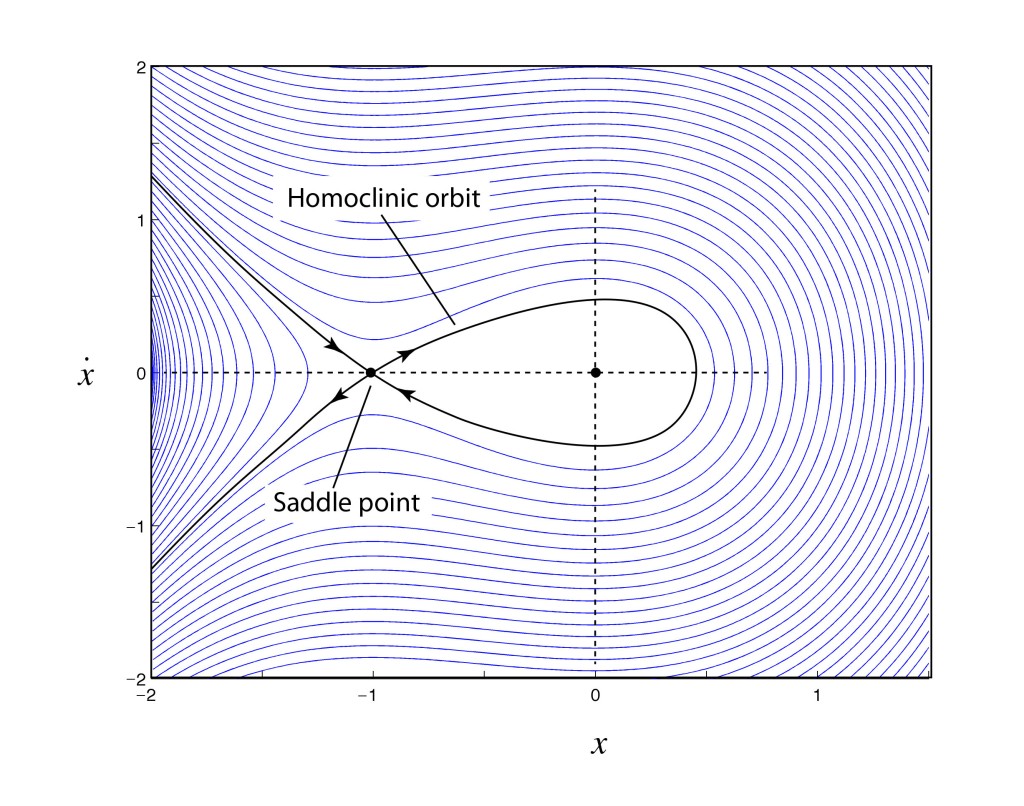
Fig. 1 A homoclinic orbit is an orbit in phase space that intersects itself.

To Poincaré’s horror, as he checked his results against the reviewer’s comments, he found that he had made a fundamental error, and in fact the solar system would never be stable.  The problem that he had overlooked had to do with the way that orbits can cross above or below each other on successive passes, leading to a tangle of orbital trajectories that crisscrossed each other in a fine mesh.  This is known as the “homoclinic tangle”: it was the first glimpse that deterministic systems could lead to unpredictable results. Most importantly, he had developed the first mathematical tools that would be needed to analyze chaotic systems—such as the Poincaré section—but nearly half a century would pass before these tools would be picked up again. 

Poincaré paid out of his own pocket for the first printing to be destroyed and for the corrected version of his manuscript to be printed in its place [1]. No-one but the competition organizers and reviewers ever saw his first version.  Yet it was when he was correcting his mistake that he stumbled on chaos for the first time, which is what posterity remembers him for. This little episode in the history of physics went undiscovered for a century before being brought to light by Barrow-Green in her 1997 book Poincaré and the Three Body Problem [2].

Fig. 2 Henri Poincaré’s homoclinic tangle from the Standard Map. (The picture on the right is the Poincaré crater on the moon). For more details, see my blog on Poincaré and his Homoclinic Tangle.

Cartwight and Littlewood (1945)

During World War II, self-oscillations and nonlinear dynamics became strategic topics for the war effort in England. High-power magnetrons were driving long-range radar, keeping Britain alert to Luftwaffe bombing raids, and the tricky dynamics of these oscillators could be represented as a driven van der Pol oscillator. These oscillators had been studied in the 1920’s by the Dutch physicist Balthasar van der Pol (1889–1959) when he was completing his PhD thesis at the University of Utrecht on the topic of radio transmission through ionized gases. van der Pol had built a short-wave triode oscillator to perform experiments on radio diffraction to compare with his theoretical calculations of radio transmission. Van der Pol’s triode oscillator was an engineering feat that produced the shortest wavelengths of the day, making van der Pol intimately familiar with the operation of the oscillator, and he proposed a general form of differential equation for the triode oscillator.

Fig. 3 Driven van der Pol oscillator equation.

Research on the radar magnetron led to theoretical work on driven nonlinear oscillators, including the discovery that a driven van der Pol oscillator could break up into wild and intermittent patterns. This “bad” behavior of the oscillator circuit (bad for radar applications) was the first discovery of chaotic behavior in man-made circuits.

These irregular properties of the driven van der Pol equation were studied by Mary- Lucy Cartwright (1990–1998) (the first woman to be elected a fellow of the Royal Society) and John Littlewood (1885–1977) at Cambridge who showed that the coexistence of two periodic solutions implied that discontinuously recurrent motion—in today’s parlance, chaos— could result, which was clearly undesirable for radar applications. The work of Cartwright and Littlewood [3] later inspired the work by Levinson and Smale as they introduced the field of nonlinear dynamics.

Fig. 4 Mary Cartwright

Andrey Kolmogorov (1954)

The passing of the Russian dictator Joseph Stalin provided a long-needed opening for Soviet scientists to travel again to international conferences where they could meet with their western colleagues to exchange ideas.  Four Russian mathematicians were allowed to attend the 1954 International Congress of Mathematics (ICM) held in Amsterdam, the Netherlands.  One of those was Andrey Nikolaevich Kolmogorov (1903 – 1987) who was asked to give the closing plenary speech.  Despite the isolation of Russia during the Soviet years before World War II and later during the Cold War, Kolmogorov was internationally renowned as one of the greatest mathematicians of his day.

By 1954, Kolmogorov’s interests had spread into topics in topology, turbulence and logic, but no one was prepared for the topic of his plenary lecture at the ICM in Amsterdam.  Kolmogorov spoke on the dusty old topic of Hamiltonian mechanics.  He even apologized at the start for speaking on such an old topic when everyone had expected him to speak on probability theory.  Yet, in the length of only half an hour he laid out a bold and brilliant outline to a proof that the three-body problem had an infinity of stable orbits.  Furthermore, these stable orbits provided impenetrable barriers to the diffusion of chaotic motion across the full phase space of the mechanical system. The crucial consequences of this short talk were lost on almost everyone who attended as they walked away after the lecture, but Kolmogorov had discovered a deep lattice structure that constrained the chaotic dynamics of the solar system.

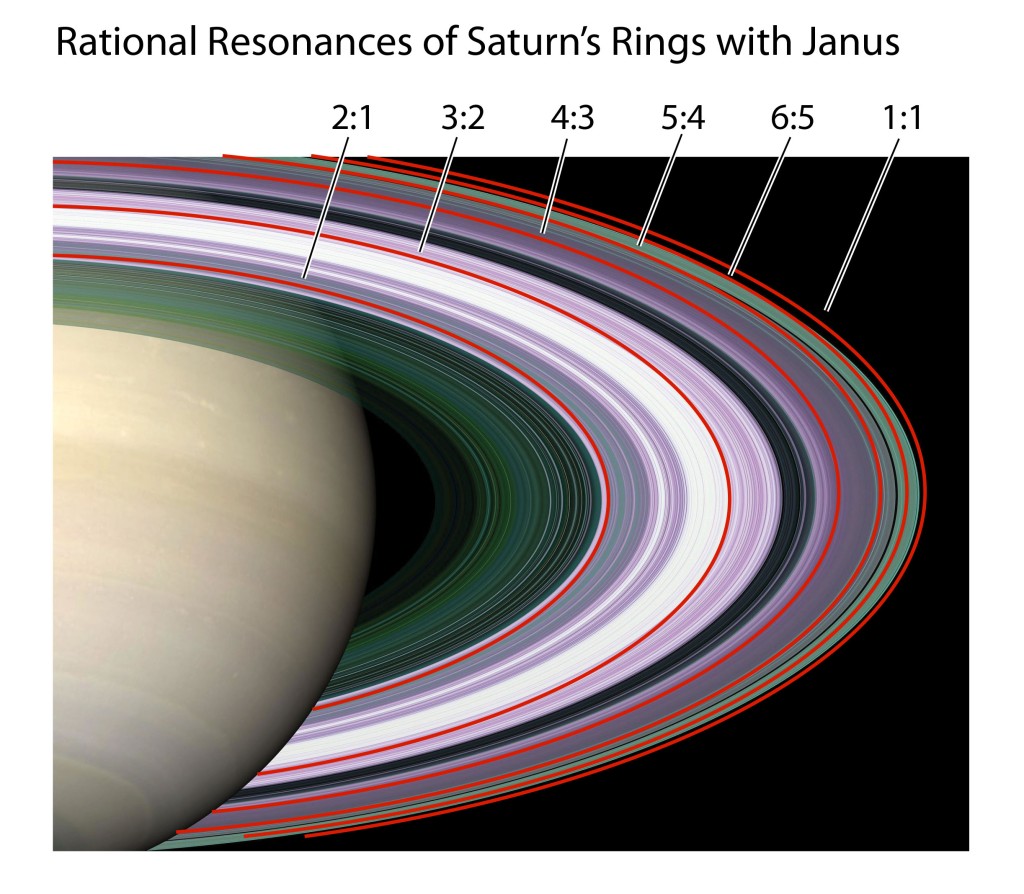
Kolmogorov’s approach used a result from number theory that provides a measure of how close an irrational number is to a rational one.  This is an important question for orbital dynamics, because whenever the ratio of two orbital periods is a ratio of integers, especially when the integers are small, then the two bodies will be in a state of resonance, which was the fundamental source of chaos in Poincaré’s stability analysis of the three-body problem.    After Komogorov had boldly presented his results at the ICM of 1954 [4], what remained was the necessary mathematical proof of Kolmogorov’s daring conjecture.  This would be provided by one of his students, V. I. Arnold, a decade later.  But before the mathematicians could settle the issue, an atmospheric scientist, using one of the first electronic computers, rediscovered Poincaré’s tangle, this time in a simplified model of the atmosphere.

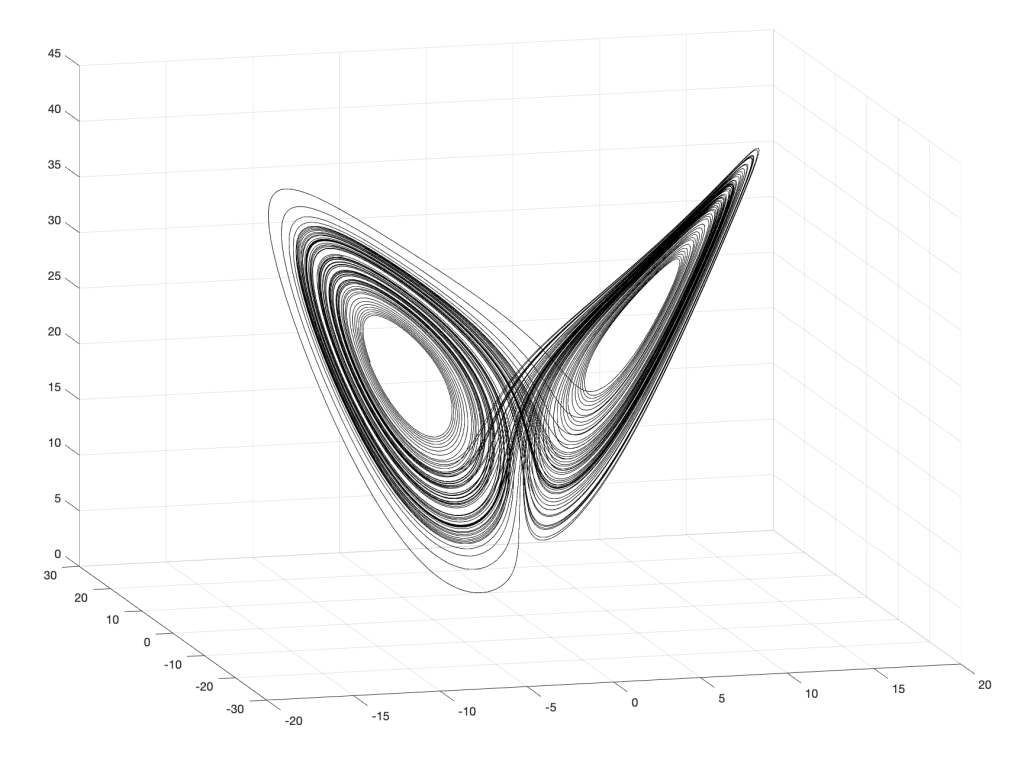
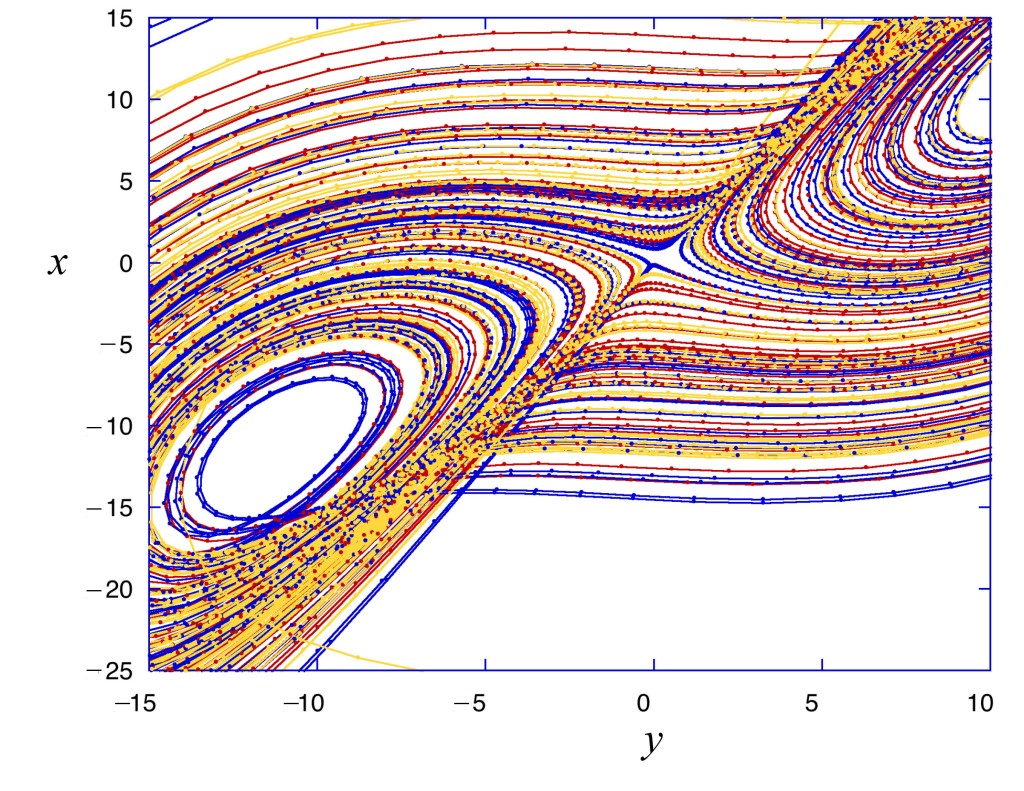
Edward Lorenz (1963)

In 1960, with the help of a friend at MIT, the atmospheric scientist Edward Lorenz purchased a Royal McBee LGP-30 tabletop computer to make calculation of a simplified model he had derived for the weather.  The McBee used 113 of the latest miniature vacuum tubes and also had 1450 of the new solid-state diodes made of semiconductors rather than tubes, which helped reduce the size further, as well as reducing heat generation.  The McBee had a clock rate of 120 kHz and operated on 31-bit numbers with a 15 kB memory.  Under full load it used 1500 Watts of power to run.  But even with a computer in hand, the atmospheric equations needed to be simplified to make the calculations tractable.  Lorenz simplified the number of atmospheric equations down to twelve, and he began programming his Royal McBee. 

Progress was good, and by 1961, he had completed a large initial numerical study.  One day, as he was testing his results, he decided to save time by starting the computations midway by using mid-point results from a previous run as initial conditions.  He typed in the three-digit numbers from a paper printout and went down the hall for a cup of coffee.  When he returned, he looked at the printout of the twelve variables and was disappointed to find that they were not related to the previous full-time run.  He immediately suspected a faulty vacuum tube, as often happened.  But as he looked closer at the numbers, he realized that, at first, they tracked very well with the original run, but then began to diverge more and more rapidly until they lost all connection with the first-run numbers.  The internal numbers of the McBee had a precision of 6 decimal points, but the printer only printed three to save time and paper.  His initial conditions were correct to a part in a thousand, but this small error was magnified exponentially as the solution progressed.  When he printed out the full six digits (the resolution limit for the machine), and used these as initial conditions, the original trajectory returned.  There was no mistake.  The McBee was working perfectly.

At this point, Lorenz recalled that he “became rather excited”.  He was looking at a complete breakdown of predictability in atmospheric science.  If radically different behavior arose from the smallest errors, then no measurements would ever be accurate enough to be useful for long-range forecasting.  At a more fundamental level, this was a break with a long-standing tradition in science and engineering that clung to the belief that small differences produced small effects.  What Lorenz had discovered, instead, was that the deterministic solution to his 12 equations was exponentially sensitive to initial conditions (known today as SIC). 

The more Lorenz became familiar with the behavior of his equations, the more he felt that the 12-dimensional trajectories had a repeatable shape.  He tried to visualize this shape, to get a sense of its character, but it is difficult to visualize things in twelve dimensions, and progress was slow, so he simplified his equations even further to three variables that could be represented in a three-dimensional graph [5]. 

Fig. 5 Two-dimensional projection of the three-dimensional Lorenz Butterfly.

V. I. Arnold (1964)

Meanwhile, back in Moscow, an energetic and creative young mathematics student knocked on Kolmogorov’s door looking for an advisor for his undergraduate thesis.  The youth was Vladimir Igorevich Arnold (1937 – 2010), who showed promise, so Kolmogorov took him on as his advisee.  They worked on the surprisingly complex properties of the mapping of a circle onto itself, which Arnold filed as his dissertation in 1959.  The circle map holds close similarities with the periodic orbits of the planets, and this problem led Arnold down a path that drew tantalizingly close to Kolmogorov’s conjecture on Hamiltonian stability.  Arnold continued in his PhD with Kolmogorov, solving Hilbert’s 13th problem by showing that every function of n variables can be represented by continuous functions of a single variable.  Arnold was appointed as an assistant in the Faculty of Mechanics and Mathematics at Moscow State University.

Arnold’s habilitation topic was Kolmogorov’s conjecture, and his approach used the same circle map that had played an important role in solving Hilbert’s 13th problem.  Kolmogorov neither encouraged nor discouraged Arnold to tackle his conjecture.  Arnold was led to it independently by the similarity of the stability problem with the problem of continuous functions.  In reference to his shift to this new topic for his habilitation, Arnold stated “The mysterious interrelations between different branches of mathematics with seemingly no connections are still an enigma for me.”  [6] 

Arnold began with the problem of attracting and repelling fixed points in the circle map and made a fundamental connection to the theory of invariant properties of action-angle variables .  These provided a key element in the proof of Kolmogorov’s conjecture.  In late 1961, Arnold submitted his results to the leading Soviet physics journal—which promptly rejected it because he used forbidden terms for the journal, such as “theorem” and “proof”, and he had used obscure terminology that would confuse their usual physicist readership, terminology such as “Lesbesgue measure”, “invariant tori” and “Diophantine conditions”.  Arnold withdrew the paper.

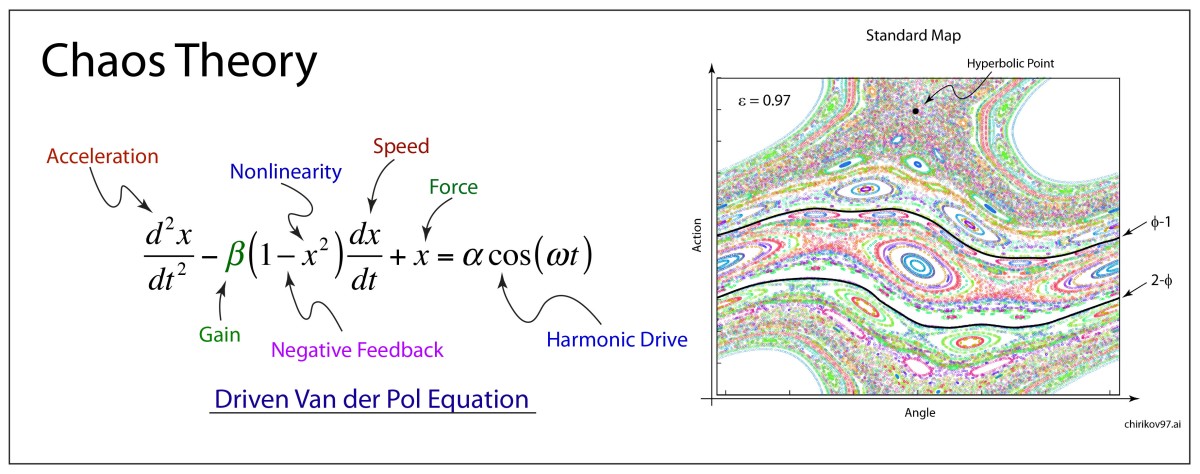
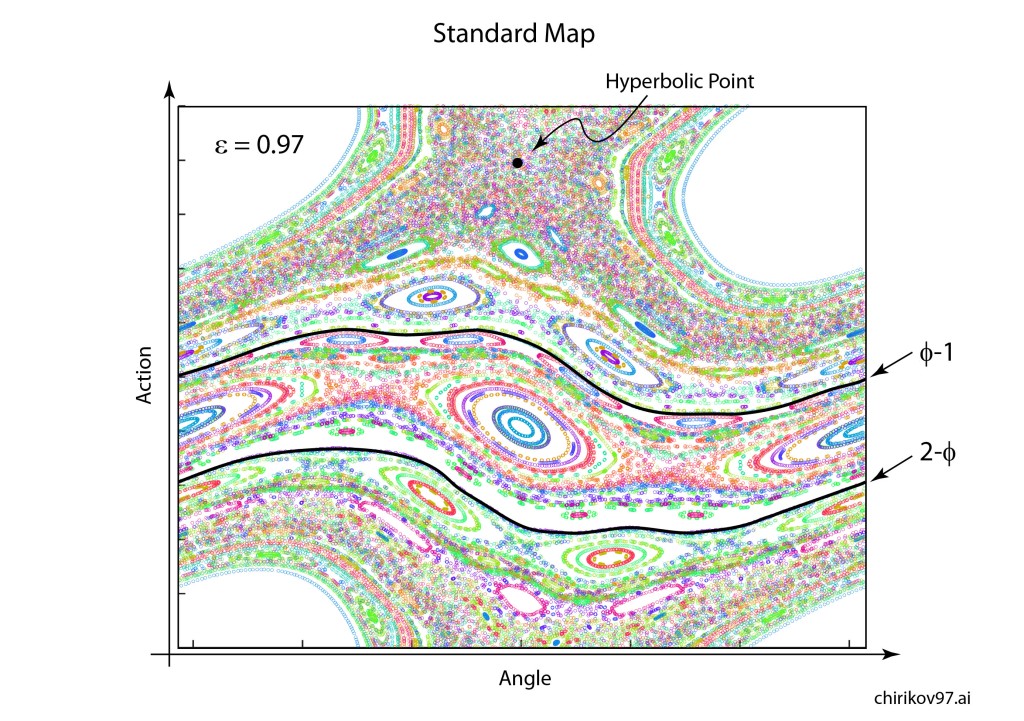
Arnold later incorporated an approach pioneered by Jurgen Moser [7] and published a definitive article on the problem of small divisors in 1963 [8].  The combined work of Kolmogorov, Arnold and Moser had finally established the stability of irrational orbits in the three-body problem, the most irrational and hence most stable orbit having the frequency of the golden mean.  The term “KAM theory”, using the first initials of the three theorists, was coined in 1968 by B. V. Chirikov, who also introduced in 1969 what has become known as the Chirikov map (also known as the Standard map ) that reduced the abstract circle maps of Arnold and Moser to simple iterated functions that any student can program easily on a computer to explore KAM invariant tori and the onset of Hamiltonian chaos, as in Fig. 1 [9]. 

Fig. 6 The Chirikov Standard Map when the last stable orbits are about to dissolve for ε = 0.97.

Sephen Smale (1967)

Stephen Smale was at the end of a post-graduate fellowship from the National Science Foundation when he went to Rio to work with Mauricio Peixoto.  Smale and Peixoto had met in Princeton in 1960 where Peixoto was working with Solomon Lefschetz  (1884 – 1972) who had an interest in oscillators that sustained their oscillations in the absence of a periodic force.  For instance, a pendulum clock driven by the steady force of a hanging weight is a self-sustained oscillator.  Lefschetz was building on work by the Russian Aleksandr A. Andronov (1901 – 1952) who worked in the secret science city of Gorky in the 1930’s on nonlinear self-oscillations using Poincaré’s first return map.  The map converted the continuous trajectories of dynamical systems into discrete numbers, simplifying problems of feedback and control. 

The central question of mechanical control systems, even self-oscillating systems, was how to attain stability.  By combining approaches of Poincaré and Lyapunov, as well as developing their own techniques, the Gorky school became world leaders in the theory and applications of nonlinear oscillations.  Andronov published a seminal textbook in 1937 The Theory of Oscillations with his colleagues Vitt and Khaykin, and Lefschetz had obtained and translated the book into English in 1947, introducing it to the West.  When Peixoto returned to Rio, his interest in nonlinear oscillations captured the imagination of Smale even though his main mathematical focus was on problems of topology.  On the beach in Rio, Smale had an idea that topology could help prove whether systems had a finite number of periodic points.  Peixoto had already proven this for two dimensions, but Smale wanted to find a more general proof for any number of dimensions.

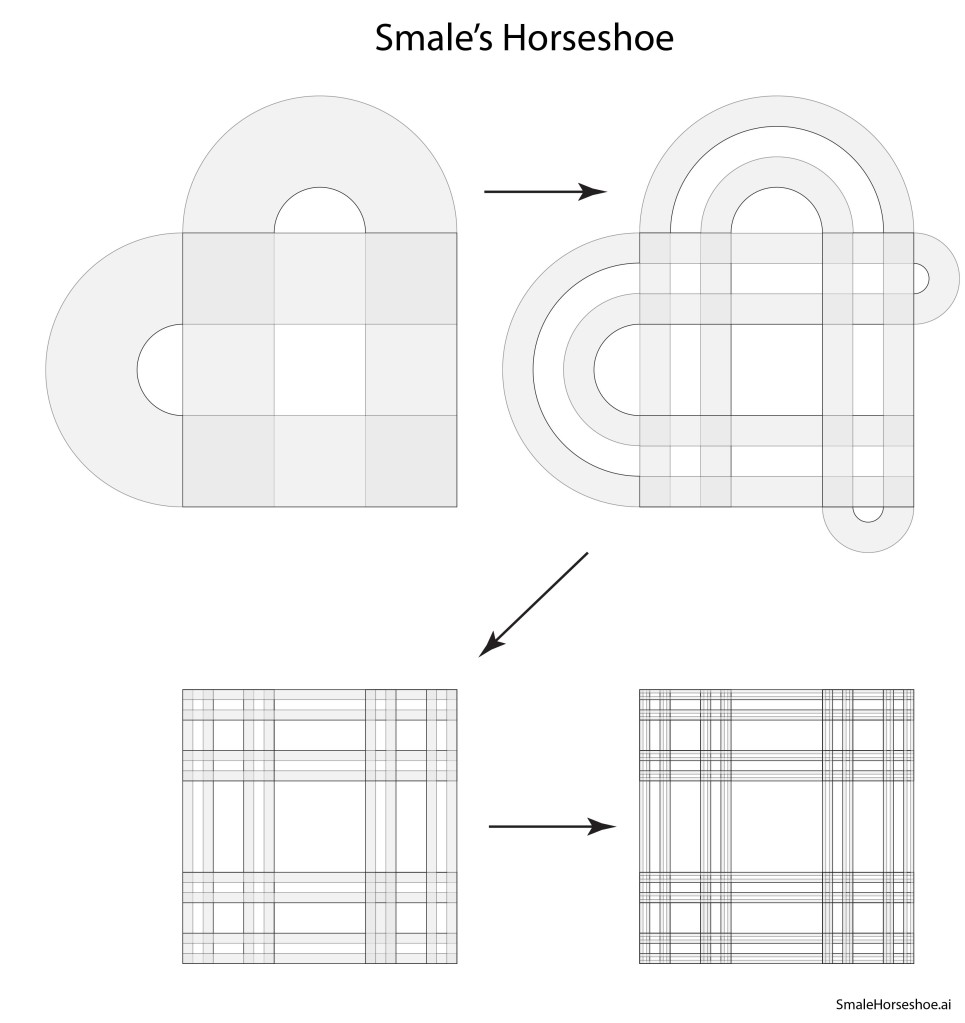
Norman Levinson (1912 – 1975) at MIT became aware of Smale’s interests and sent off a letter to Rio in which he suggested that Smale should look at Levinson’s work on the triode self-oscillator (a van der Pol oscillator), as well as the work of Cartwright and Littlewood who had discovered quasi-periodic behavior hidden within the equations.  Smale was puzzled but intrigued by Levinson’s paper that had no drawings or visualization aids, so he started scribbling curves on paper that bent back upon themselves in ways suggested by the van der Pol dynamics.  During a visit to Berkeley later that year, he presented his preliminary work, and a colleague suggested that the curves looked like strips that were being stretched and bent into a horseshoe. 

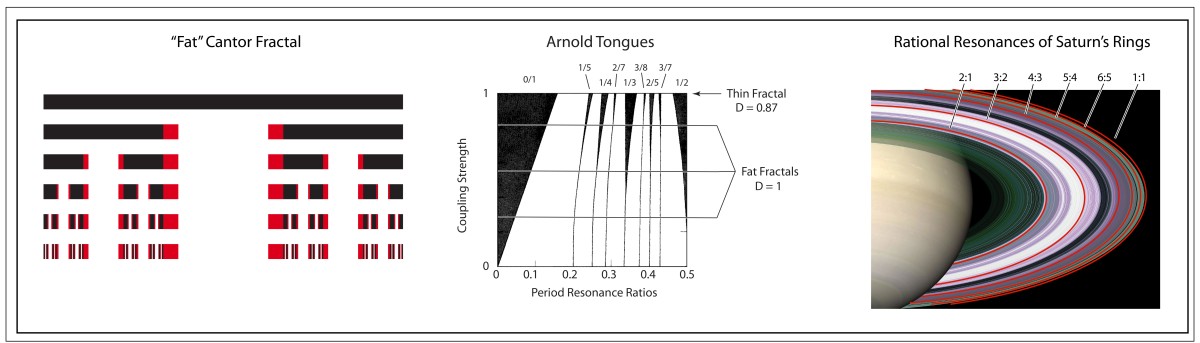
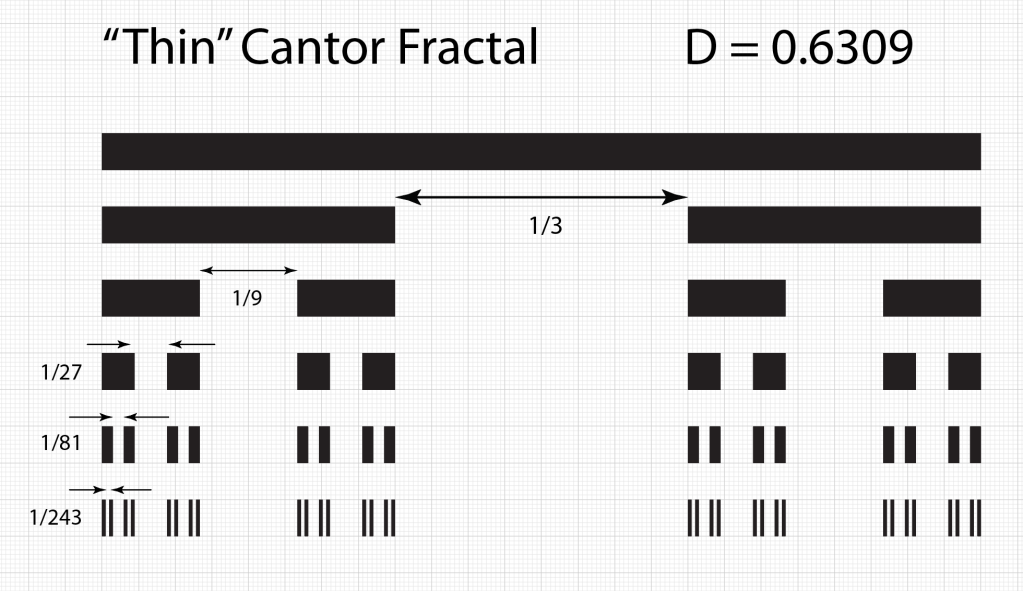
Smale latched onto this idea, realizing that the strips were being successively stretched and folded under the repeated transformation of the dynamical equations.  Furthermore, because dynamics can move forward in time as well as backwards, there was a sister set of horseshoes that were crossing the original set at right angles.  As the dynamics proceeded, these two sets of horseshoes were repeatedly stretched and folded across each other, creating an infinite latticework of intersections that had the properties of the Cantor set.  Here was solid proof that Smale’s original conjecture was wrong—the dynamics had an infinite number of periodicities, and they were nested in self-similar patterns in a latticework of points that map out a Cantor-like set of points.  In the two-dimensional case, shown in the figure, the fractal dimension of this lattice is D = ln4/ln3 = 1.26, somewhere in dimensionality between a line and a plane.  Smale’s infinitely nested set of periodic points was the same tangle of points that Poincaré had noticed while he was correcting his King Otto Prize manuscript.  Smale, using modern principles of topology, was finally able to put rigorous mathematical structure to Poincaré’s homoclinic tangle. Coincidentally, Poincaré had launched the modern field of topology, so in a sense he sowed the seeds to the solution to his own problem.

Fig. 7 The horseshoe takes regions of phase space and stretches and folds them over and over to create a lattice of overlapping trajectories.

Ruelle and Takens (1971)

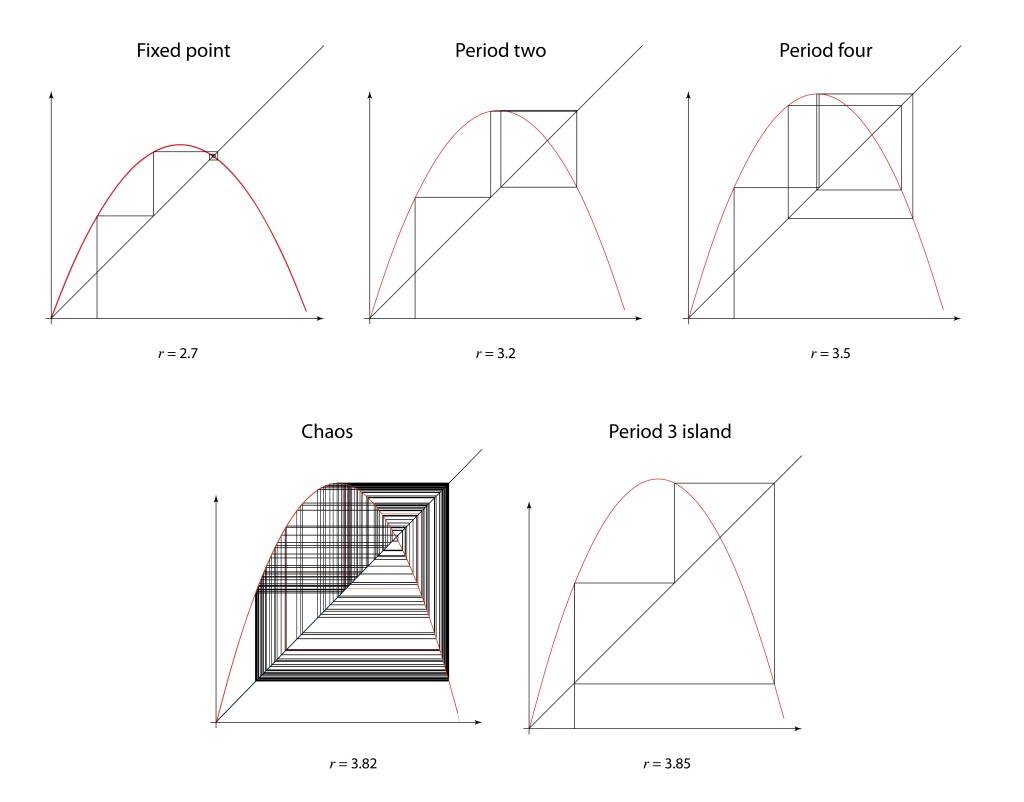
The onset of turbulence was an iconic problem in nonlinear physics with a long history and a long list of famous researchers studying it.  As far back as the Renaissance, Leonardo da Vinci had made detailed studies of water cascades, sketching whorls upon whorls in charcoal in his famous notebooks.  Heisenberg, oddly, wrote his PhD dissertation on the topic of turbulence even while he was inventing quantum mechanics on the side.  Kolmogorov in the 1940’s applied his probabilistic theories to turbulence, and this statistical approach dominated most studies up to the time when David Ruelle and Floris Takens published a paper in 1971 that took a nonlinear dynamics approach to the problem rather than statistical, identifying strange attractors in the nonlinear dynamical Navier-Stokes equations [10].  This paper coined the phrase “strange attractor”.  One of the distinct characteristics of their approach was the identification of a bifurcation cascade.  A single bifurcation means a sudden splitting of an orbit when a parameter is changed slightly.  In contrast, a bifurcation cascade was not just a single Hopf bifurcation, as seen in earlier nonlinear models, but was a succession of Hopf bifurcations that doubled the period each time, so that period-two attractors became period-four attractors, then period-eight and so on, coming fast and faster, until full chaos emerged.  A few years later Gollub and Swinney experimentally verified the cascade route to turbulence , publishing their results in 1975 [11]. 

Fig. 8 Bifurcation cascade of the logistic map.

Feigenbaum (1978)

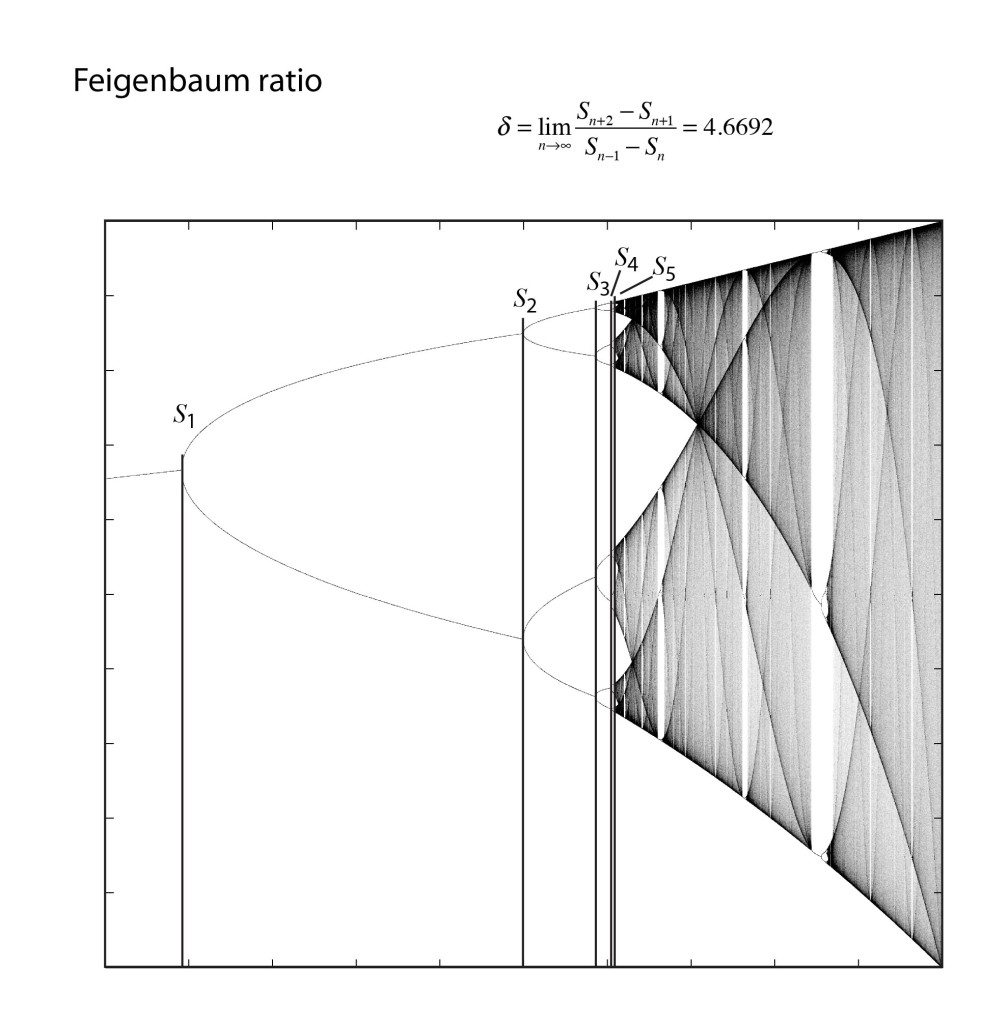
In 1976, computers were not common research tools, although hand-held calculators now were.  One of the most famous of this era was the Hewlett-Packard HP-65, and Feigenbaum pushed it to its limits.  He was particularly interested in the bifurcation cascade of the logistic map [12]—the way that bifurcations piled on top of bifurcations in a forking structure that showed increasing detail at increasingly fine scales.  Feigenbaum was, after all, a high-energy theorist and had overlapped at Cornell with Kenneth Wilson when he was completing his seminal work on the renormalization group approach to scaling phenomena.  Feigenbaum recognized a strong similarity between the bifurcation cascade and the ideas of real-space renormalization where smaller and smaller boxes were used to divide up space. 

One of the key steps in the renormalization procedure was the need to identify a ratio of the sizes of smaller structures to larger structures.  Feigenbaum began by studying how the bifurcations depended on the increasing growth rate.  He calculated the threshold values rm for each of the bifurcations, and then took the ratios of the intervals, comparing the previous interval (rm-1 – rm-2) to the next interval (rm – rm-1).  This procedure is like the well-known method to calculate the golden ratio = 1.61803 from the Fibonacci series, and Feigenbaum might have expected the golden ratio to emerge from his analysis of the logistic map.  After all, the golden ratio has a scary habit of showing up in physics, just like in the KAM theory.  However, as the bifurcation index m increased in Feigenbaum’s study, this ratio settled down to a limiting value of 4.66920.  Then he did what anyone would do with an unfamiliar number that emerges from a physical calculation—he tried to see if it was a combination of other fundamental numbers, like pi and Euler’s constant e, and even the golden ratio.  But none of these worked.  He had found a new number that had universal application to chaos theory [13]. 

Fig. 9 The ratio of the limits of successive cascades leads to a new universal number (the Feigenbaum number).

Gleick (1987)

By the mid-1980’s, chaos theory was seeping in to a broadening range of research topics that seemed to span the full breadth of science, from biology to astrophysics, from mechanics to chemistry. A particularly active group of chaos practitioners were J. Doyn Farmer, James Crutchfield, Norman Packard and Robert Shaw who founded the Dynamical Systems Collective at the University of California, Santa Cruz. One of the important outcomes of their work was a method to reconstruct the state space of a complex system using only its representative time series [14]. Their work helped proliferate the techniques of chaos theory into the mainstream. Many who started using these techniques were only vaguely aware of its long history until the science writer James Gleick wrote a best-selling history of the subject that brought chaos theory to the forefront of popular science [15]. And the rest, as they say, is history.

References

[1] Poincaré, H. and D. L. Goroff (1993). New methods of celestial mechanics. Edited and introduced by Daniel L. Goroff. New York, American Institute of Physics.

[2] J. Barrow-Green, Poincaré and the three body problem (London Mathematical Society, 1997).

[3] Cartwright,M.L.andJ.E.Littlewood(1945).“Onthenon-lineardifferential equation of the second order. I. The equation y′′ − k(1 – yˆ2)y′ + y = bλk cos(λt + a), k large.” Journal of the London Mathematical Society 20: 180–9. Discussed in Aubin, D. and A. D. Dalmedico (2002). “Writing the History of Dynamical Systems and Chaos: Longue DurÈe and Revolution, Disciplines and Cultures.” Historia Mathematica, 29: 273.

[4] Kolmogorov, A. N., (1954). “On conservation of conditionally periodic motions for a small change in Hamilton’s function.,” Dokl. Akad. Nauk SSSR (N.S.), 98: 527–30.

[5] Lorenz, E. N. (1963). “Deterministic Nonperiodic Flow.” Journal of the Atmo- spheric Sciences 20(2): 130–41.

[6] Arnold,V.I.(1997).“From superpositions to KAM theory,”VladimirIgorevich Arnold. Selected, 60: 727–40.

[7] Moser, J. (1962). “On Invariant Curves of Area-Preserving Mappings of an Annulus.,” Nachr. Akad. Wiss. Göttingen Math.-Phys, Kl. II, 1–20.

[8] Arnold, V. I. (1963). “Small denominators and problems of the stability of motion in classical and celestial mechanics (in Russian),” Usp. Mat. Nauk., 18: 91–192,; Arnold, V. I. (1964). “Instability of Dynamical Systems with Many Degrees of Freedom.” Doklady Akademii Nauk Sssr 156(1): 9.

[9] Chirikov, B. V. (1969). Research concerning the theory of nonlinear resonance and stochasticity. Institute of Nuclear Physics, Novosibirsk. 4. Note: The Standard Map Jn+1 =Jn +εsinθn θn+1 =θn +Jn+1
is plotted in Fig. 3.31 in Nolte, Introduction to Modern Dynamics (2015) on p. 139. For small perturbation ε, two fixed points appear along the line J = 0 corresponding to p/q = 1: one is an elliptical point (with surrounding small orbits) and the other is a hyperbolic point where chaotic behavior is first observed. With increasing perturbation, q elliptical points and q hyperbolic points emerge for orbits with winding numbers p/q with small denominators (1/2, 1/3, 2/3 etc.). Other orbits with larger q are warped by the increasing perturbation but are not chaotic. These orbits reside on invariant tori, known as the KAM tori, that do not disintegrate into chaos at small perturbation. The set of KAM tori is a Cantor-like set with non- zero measure, ensuring that stable behavior can survive in the presence of perturbations, such as perturbation of the Earth’s orbit around the Sun by Jupiter. However, with increasing perturbation, orbits with successively larger values of q disintegrate into chaos. The last orbits to survive in the Standard Map are the golden mean orbits with p/q = φ–1 and p/q = 2–φ. The critical value of the perturbation required for the golden mean orbits to disintegrate into chaos is surprisingly large at εc = 0.97.

[10] Ruelle,D. and F.Takens (1971).“OntheNatureofTurbulence.”Communications in Mathematical Physics 20(3): 167–92.

[11] Gollub, J. P. and H. L. Swinney (1975). “Onset of Turbulence in a Rotating Fluid.” Physical Review Letters, 35(14): 927–30.

[12] May, R. M. (1976). “Simple Mathematical-Models with very complicated Dynamics.” Nature, 261(5560): 459–67.

[13] M. J. Feigenbaum, “Quantitative Universality for a Class of Nnon-linear Transformations,” Journal of Statistical Physics 19, 25-52 (1978).

[14] Packard, N.; Crutchfield, J. P.; Farmer, J. Doyne; Shaw, R. S. (1980). “Geometry from a Time Series”. Physical Review Letters. 45 (9): 712–716.

[15] Gleick,J.(1987).Chaos:MakingaNewScience,NewYork:Viking.p.180.

by David D. Nolte

Fat Fractals, Arnold Tongues, and the Rings of Saturn

Fractals, those telescoping self-similar filigree meshes that marry mathematics and art, have become so mainstream, that they are even mentioned in the theme song of Disney’s 2013 mega-hit, Frozen. 

My power flurries through the air into the ground
My soul is spiraling in frozen fractals all around
And one thought crystallizes like an icy blast
I’m never going back, the past is in the past

Let it Go, by Idina Menzel (Frozen, Disney 2013)

But not all fractals are cut from the same cloth.  Some are thin and some are fat.  The thin ones are the ones we know best, adorning the cover of books and magazines.  But the fat ones may be more common and may play important roles, such as in the stability of celestial orbits in a many-planet neighborhood, or in the stability and structure of Saturn’s rings.

To get a handle on fat fractals, we will start with a familiar thin one, the zero-measure Cantor set.

The Zero-Measure Cantor Set

The famous one-third Cantor set is often the first fractal that you encounter in any introduction to fractals. (See my blog on a short history of fractals.)  It lives on a one-dimensional line, and its iterative construction is intuitive and simple.

Start with a long thin bar of unit length.  Then remove the middle third, leaving the endpoints.  This leaves two identical bars of one-third length each.  Next, remove the open middle third of each of these, again leaving the endpoints, leaving behind section pairs of one-nineth length.  Then repeat ad infinitum.  The points of the line that remain–all those segment endpoints–are the Cantor set.

Fig. 1 Construction of the 1/3 Cantor set by removing 1/3 segments at each level, and leaving the endpoints of each segment. The resulting set is a dust of points with a fractal dimension D = ln(2)/ln(3) = 0.6309.

The Cantor set has a fractal dimension that is easily calculated by noting that at each stage there are two elements (N = 2) that divided by three in size (b = 3).  The fractal dimension is then

It is easy to prove that the collection of points of the Cantor set have no length because all of the length was removed. 

For instance, at the first level, one third of the length was removed.  At the second level, two segments of one-nineth length were removed.  At the third level, four segments of one-twenty-sevength length were removed, and so on.  Mathematically, this is

The infinite series in the brackets is a binomial series with the simple solution

Therefore, all the length has been removed, and none is left to the Cantor set, which is simply a collection of all the endpoints of all the segments that were removed.

The Cantor set is said to have a Lebesgue measure of zero.  It behaves as a dust of isolated points.

A close relative of the Cantor set is the Sierpinski Carpet which is the two-dimensional analog.  It begins with a square of unit side, then the middle third is removed (one nineth of the three-by-three array of square of one-third side), and so on.

Fig. 2 A regular Sierpinski Carpet with fractal dimension D = ln(8)/ln(3) = 1.8928.

The resulting Sierpinski Carpet has zero Lebesgue measure, just like the Cantor dust, because all the area has been removed.

There are also random Sierpinski Carpets as the sub-squares are removed from random locations. 

Fig. 3 A random Sierpinski Carpet with fractal dimension D = ln(8)/ln(3) = 1.8928.

These fractals are “thin”, so-called because they are dusts with zero measure.

But the construction was constructed just so, such that the sum over all the removed sub-lengths summed to unity.  What if less material had been taken at each step?  What happens?

Fat Fractals

Instead of taking one-third of the original length, take instead one-fourth.  But keep the one-third scaling level-to-level, as for the original Cantor Set.

Fig. 4 A “fat” Cantor fractal constructed by removing 1/4 of a segment at each level instead of 1/3.

The total length removed is

Therefore, three fourths of the length was removed, leaving behind one fourth of the material.  Not only that, but the material left behind is contiguous—solid lengths.  At each level, a little bit of the original bar remains, and still remains at the next level and the next. Therefore, it is said to have a Lebesgue measure of unity.  This construction leads to a “fat” fractal.

Fig. 5 Fat Cantor fractal showing the original Cantor 1/3 set (in black) and the extra contiguous segments (in red) that give the set a Lebesgue measure equal to one.

Looking at Fig. 5, it is clear that the original Cantor dust is still present as the black segments interspersed among the red parts of the bar that are contiguous.  But when two sets are added that have different “dimensions”, then the combined set has the larger dimension of the two, which is one-dimensional in this case.  The fat Cantor set is one dimensional.  One can still study its scaling properties, leading to another type of dimension known as an exterior measure [1], but where do such fat fractals occur? Why do they matter?

One answer is that they lie within the oddly named “Arnold Tongues” that arise in the study of synchronization and resonance connected to the stability of the solar system and the safety of its inhabitants.

Arnold Tongues

The study of synchronization explores and explains how two or more non-identical oscillators can lock themselves onto a common shared oscillation. For two systems to synchronize requires autonomous oscillators (like planetary orbits) with a period-dependent interaction (like gravity). Such interactions are “resonant” when the periods of the two orbits are integer ratios of each other, like 1:2 or 2:3. Such resonances ensure that there is a periodic forcing caused by the interaction that is some multiple of the orbital period. Think of tapping a rotating bicycle wheel twice per cycle or three times per cycle. Even if you are a little off in your timing, you can lock the tire rotation rate to a multiple of your tapping frequency. But if you are too far off on your timing, then the wheel will turn independently of your tapping.

Because rational ratios of integers are plentiful, there can be an intricate interplay between locked frequencies and unlocked frequencies. When the rotation rate is close to a resonance, then the wheel can frequency-lock to the tapping. Plotting the regions where the wheel synchronizes or not as a function of the frequency ratio and also as a function of the strength of the tapping leads to one of the iconic images of nonlinear dynamics: the Arnold tongue diagram.

Fig. 6 Arnold tongue diagram, showing the regions of frequency locking (black) at rational resonances as a function of coupling strength. At unity coupling strength, the set outside frequency-locked regions is fractal with D = 0.87. For all smaller coupling, a set along a horizontal is a fat fractal with topological dimension D = 1. The white regions are “ergodic”, as the phase of the oscillator runs through all possible values.

The Arnold tongues in Fig. 6 are the frequency locked regions (black) as a function of frequency ratio and coupling strength g. The black regions correspond to rational ratios of frequencies. For g = 1, the set outside frequency-locked regions (the white regions are “ergodic”, as the phase of the oscillator runs through all possible values) is a thin fractal with D = 0.87. For g < 1, the sets outside the frequency locked regions along a horizontal (at constant g) are fat fractals with topological dimension D = 1. For fat fractals, the fractal dimension is irrelevant, and another scaling exponent takes on central importance.

The Lebesgue measure μ of the ergodic regions (the regions that are not frequency locked) is a function of the coupling strength varying from μ = 1 at g = 0 to μ = 0 at g = 1. When the pattern is coarse-grained at a scale ε, then the scaling of a fat fractal is

where β is the scaling exponent that characterizes the fat fractal.

From numerical studies [2] there is strong evidence that β = 2/3 for the fat fractals of Arnold Tongues.

The Rings of Saturn

Arnold Tongues arise in KAM theory on the stability of the solar system (See my blog on KAM and how number theory protects us from the chaos of the cosmos). Fortunately, Jupiter is the largest perturbation to Earth’s orbit, but its influence, while non-zero, is not enough to seriously affect our stability. However, there is a part of the solar system where rational resonances are not only large but dominant: Saturn’s rings.

Saturn’s rings are composed of dust and ice particles that orbit Saturn with a range of orbital periods. When one of these periods is a rational fraction of the orbital period of a moon, then a resonance condition is satisfied. Saturn has many moons, producing highly corrugated patterns in Saturn’s rings at rational resonances of the periods.

Fig. 7 A close up of Saturn’s rings shows a highly detailed set of bands. Particles at a given radius have a given period (set by Kepler’s third law). When the period of dust particles in the ring are an integer ratio of the period of a “shepherd moon”, then a resonance can drive density rings. [See image reference.]

The moons Janus and Epithemeus share an orbit around Saturn in a rare 1:1 resonance in which they swap positions every four years. Their combined gravity excites density ripples in Saturn’s rings, photographed by the Cassini spacecraft and shown in Fig. 8.

Fig. 8 Cassini spacecraft photograph of density ripples in Saturns rings caused by orbital resonance with the pair of moons Janus and Epithemeus.

One Canadian astronomy group converted the resonances of the moon Janus into a musical score to commenorate Cassini’s final dive into the planet Saturn in 2017. The Janus resonances are shown in Fig. 9 against the pattern of Saturn’s rings.

Fig. 7 Rational resonances for subrings of Saturn relative to its moon Janus.

Saturn’s rings, orbital resonances, Arnold tongues and fat fractals provide a beautiful example of the power of dynamics to create structure, and the primary role that structure plays in deciphering the physics of complex systems.

References:

[1] C. Grebogi, S. W. McDonald, E. Ott, and J. A. Yorke, “EXTERIOR DIMENSION OF FAT FRACTALS,” Physics Letters A 110, 1-4 (1985).

[2] R. E. Ecke, J. D. Farmer, and D. K. Umberger, “Scaling of the Arnold tongues,” Nonlinearity 2, 175-196 (1989).

by David D. Nolte

Climate Change Physics 101

When our son was ten years old, he came home from a town fair in Battleground, Indiana, with an unwanted pet—a goldfish in a plastic bag.  The family rushed out to buy a fish bowl and food and plopped the golden-red animal into it.  In three days, it was dead!

It turns out that you can’t just put a gold fish in a fish bowl.  When it metabolizes its food and expels its waste, it builds up toxic levels of ammonia unless you add filters or plants or treat the water with chemicals.  In the end, the goldfish died because it was asphyxiated by its own pee.

It’s a basic rule—don’t pee in your own fish bowl.

The same can be said for humans living on the surface of our planet.  Polluting the atmosphere with our wastes cannot be a good idea.  In the end it will kill us.  The atmosphere may look vast—the fish bowl was a big one—but it is shocking how thin it is.

Turn on your Apple TV, click on the screen saver, and you are skimming over our planet on the dark side of the Earth. Then you see a thin blue line extending over the limb of the dark disc.  Hold!  That thin blue line!  That is our atmosphere! Is it really so thin?

When you look upwards on a clear sunny day, the atmosphere seems like it goes on forever.  It doesn’t.  It is a thin veneer on the surface of the Earth barely one percent of the Earth’s radius.  The Earth’s atmosphere is frighteningly thin. 

Fig. 1  A thin veneer of atmosphere paints the surface of the Earth.  The radius of the Earth is 6360 km, and the thickness of the atmosphere is 100 km, which is a bit above 1 percent of the radius.

Consider Mars.  It’s half the size of Earth, yet it cannot hold on to an atmosphere even 1/100th the thickness of ours.  When Mars first formed, it had an atmosphere not unlike our own, but through the eons its atmosphere has wafted away irretrievably into space.

An atmosphere is a precious fragile thing for a planet.  It gives life and it gives protection.  It separates us from the deathly cold of space, holding heat like a blanket.  That heat has served us well over the eons, allowing water to stay liquid and allowing life to arise on Earth.  But too much of a good thing is not a good thing.

Common Sense

If the fluid you are bathed in gives you life, then don’t mess with it.  Don’t run your car in the garage while you are working in it.  Don’t use a charcoal stove in an enclosed space.  Don’t dump carbon dioxide into the atmosphere because it also is an enclosed space.

At the end of winter, as the warm spring days get warmer, you take the winter blanket off your bed because blankets hold in heat.  The thicker the blanket, the more heat it holds in.  Common sense tells you to reduce the thickness of the blanket if you don’t want to get too warm.  Carbon dioxide in the atmosphere acts like a blanket.  If we don’t want the Earth to get too warm, then we need to limit the thickness of the blanket.

Without getting into the details of any climate change model, common sense already tells us what we should do.  Keep the atmosphere clean and stable (Don’t’ pee in our fishbowl) and limit the amount of carbon dioxide we put into it (Don’t let the blanket get too thick).

Some Atmospheric Facts

Here are some facts about the atmosphere, about the effect humans have on it, and about the climate:

Fact 1.  Humans have increased the amount of carbon dioxide in the atmosphere by 45% since 1850 (the beginning of the industrial age) and by 30% since just 1960.

Fact 2.  Carbon dioxide in the atmosphere prevents some of the heat absorbed from the Sun to re-radiate out to space.  More carbon dioxide stores more heat.

Fact 3.  Heat added to the Earth’s atmosphere increases its temperature.  This is a law of physics.

Fact 4.  The Earth’s average temperature has risen by 1.2 degrees Celsius since 1850 and 0.8 degrees of that has been just since 1960, so the effect is accelerating.

These facts are indisputable.  They hold true regardless of whether there is a Republican or a Democrat in the White House or in control of Congress.

There is another interesting observation which is not so direct, but may hold a harbinger for the distant future: The last time the Earth was 3 degrees Celsius warmer than it is today was during the Pliocene when the sea level was tens of meters higher.  If that sea level were to occur today, all of Delaware, most of Florida, half of Louisiana and the entire east coast of the US would be under water, including Houston, Miami, New Orleans, Philadelphia and New York City.  There are many reasons why this may not be an immediate worry. The distribution of water and ice now is different than in the Pliocene, and the effect of warming on the ice sheets and water levels could take centuries. Within this century, the amount of sea level rise is likely to be only about 1 meter, but accelerating after that.

Fig. 2  The east coast of the USA for a sea level 30 meters higher than today.  All of Delaware, half of Louisiana, and most of Florida are under water. Reasonable projections show only a 1 meter sea level rise by 2100, but accelerating after that. From https://www.youtube.com/watch?v=G2x1bonLJFA

Balance and Feedback

It is relatively easy to create a “rule-of-thumb” model for the Earth’s climate (see Ref. [2]).  This model is not accurate, but it qualitatively captures the basic effects of climate change and is a good way to get an intuitive feeling for how the Earth responds to changes, like changes in CO2 or to the amount of ice cover.  It can also provide semi-quantitative results, so that relative importance of various processes or perturbations can be understood.

The model is a simple energy balance statement:  In equilibrium, as much energy flows into the Earth system as out.

This statement is both simple and immediately understandable.  But then the work starts as we need to pin down how much energy is flowing in and how much is flowing out.  The energy flowing in comes from the sun, and the energy flowing out comes from thermal radiation into space. 

We also need to separate the Earth system into two components: the surface and the atmosphere.  These are two very different things that have two different average temperatures.  In addition, the atmosphere transmits sunlight to the surface, unless clouds reflect it back into space.  And the Earth radiates thermally into space, unless clouds or carbon dioxide layers reflect it back to the surface.

The energy fluxes are shown in the diagram in Fig. 3 for the 4-component system: Sun, Surface, Atmosphere, and Space. The light from the sun, mostly in the visible range of the spectrum, is partially absorbed by the atmosphere and partially transmitted and reflected. The transmitted portion is partially absorbed and partially reflected by the surface. The heat of the Earth is radiated at long wavelengths to the atmosphere, where it is partially transmitted out into space, but also partially reflected by the fraction a’a which is the blanket effect. In addition, the atmosphere itself radiates in equal parts to the surface and into outer space. On top of all of these radiative processes, there is also non-radiative convective interaction between the atmosphere and the surface.

Fig. 3 Energy flux model for a simple climate model with four interacting systems: the Sun, the Atmosphere, the Earth and Outer Space.

These processes are captured by two energy flux equations, one for the atmosphere and one for the surface, in Fig. 4. The individual contributions from Fig. 3 are annotated in each case. In equilibrium, each flux equals zero, which can then be used to solve for the two unknowns: Ts0 and Ta0: the surface and atmosphere temperatures.

Fig. 4 Energy-balance model of the Earth’s atmosphere for a simple climate approximation.

After the equilibrium temperatures Ts0 and Ta0 are found, they go into a set of dynamic response equations that governs how deviations in the temperatures relax back to the equilibrium values. These relaxation equations are

where ks and ka are the relaxation rates for the surface and atmosphere. These can be quite slow, in the range of a century. For illustration, we can take ks = 1/75 years and ka = 1/25 years. The equilibrium temperatures for the surface and atmosphere differ by about 50 degrees Celsius, with Ts = 289 K and Ta = 248 K. These are rough averages over the entire planet. The solar constant is S = 1.36×103 W/m2, the Stefan-Boltzman constant is σ = 5.67×10-8 W/m2/K4, and the convective interaction constant is c = 2.5 W m-2 K-1. Other parameters are given in Table I.

Short WavelengthLong Wavelength
as = 0.11
ts = 0.53t’a = 0.06
aa = 0.30a’a = 0.31

The relaxation equations are in the standard form of a mathematical “flow” (see Ref. [1]) and the solutions are plotted as a phase-space portrait in Fig. 5 as a video of the flow as the parameters in Table I shift because of the addition of greenhouse gases to the atmosphere. The video runs from the year 1850 (the dawn of the industrial age) through to the year 2060 about 40 years from now.

Fig. 5 Video of the phase space flow of the Surface-Atmosphere system for increasing year. The flow vectors and flow lines are the relaxation to equilibrium for temperature deviations. The change in equilibrium over the years is from increasing blanket effects in the atmosphere caused by greenhouse gases.

The scariest part of the video is how fast it accelerates. From 1850 to 1950 there is almost no change, but then it accelerates, faster and faster, reflecting the time-lag in temperature rise in response to increased greenhouse gases.

What if the Models are Wrong?  Russian Roulette

Now come the caveats.

This model is just for teaching purposes, not for any realistic modeling of climate change. It captures the basic physics, and it provides a semi-quantitative set of parameters that leads to roughly accurate current temperatures. But of course, the biggest elephant in the room is that it averages over the entire planet, which is a very crude approximation.

It does get the basic facts correct, though, showing an alarming trend in the rise in average temperatures with the temperature rising by 3 degrees by 2060.

The professionals in this business have computer models that are orders of magnitude more more accurate than this one. To understand the details of the real climate models, one needs to go to appropriate resources, like this NOAA link, this NASA link, this national climate assessment link, and this government portal link, among many others.

One of the frequent questions that is asked is: What if these models are wrong? What if global warming isn’t as bad as these models say? The answer is simple: If they are wrong, then the worst case is that life goes on. If they are right, then in the worst case life on this planet may end.

It’s like playing Russian Roulette. If just one of the cylinders on the revolver has a live bullet, do you want to pull the trigger?

Matlab Code

function flowatmos.m

mov_flag = 1;
if mov_flag == 1
    moviename = 'atmostmp';
    aviobj = VideoWriter(moviename,'MPEG-4');
    aviobj.FrameRate = 12;
    open(aviobj);
end

Solar = 1.36e3;		% Solar constant outside atmosphere [J/sec/m2]
sig = 5.67e-8;		% Stefan-Boltzman constant [W/m2/K4]

% 1st-order model of Earth + Atmosphere

ta = 0.53;			% (0.53)transmissivity of air
tpa0 = 0.06;			% (0.06)primes are for thermal radiation
as0 = 0.11;			% (0.11)
aa0 = 0.30;			% (0.30)
apa0 = 0.31;        % (0.31)
c = 2.5;               % W/m2/K

xrange = [287 293];
yrange = [247 251];

rngx = xrange(2) - xrange(1);
rngy = yrange(2) - yrange(1);

[X,Y] = meshgrid(xrange(1):0.05:xrange(2), yrange(1):0.05:yrange(2));

smallarrow = 1;
Delta0 = 0.0000009;
for tloop =1:80
    
    Delta = Delta0*(exp((tloop-1)/8)-1);   % This Delta is exponential, but should become more linear over time
    date = floor(1850 + (tloop-1)*(2060-1850)/79);
    
    [x,y] = f5(X,Y);
    
    clf
    hold off
    eps = 0.002;
    for xloop = 1:11
        xs = xrange(1) +(xloop-1)*rngx/10 + eps;
        for yloop = 1:11
            ys = yrange(1) +(yloop-1)*rngy/10 + eps;
            
            streamline(X,Y,x,y,xs,ys)
            
        end
    end
    hold on
    [XQ,YQ] = meshgrid(xrange(1):1:xrange(2),yrange(1):1:yrange(2));
    smallarrow = 1;
    [xq,yq] = f5(XQ,YQ);
    quiver(XQ,YQ,xq,yq,.2,'r','filled')
    hold off
    
    axis([xrange(1) xrange(2) yrange(1) yrange(2)])
    set(gcf,'Color','White')
    
    fun = @root2d;
    x0 = [0 -40];
    x = fsolve(fun,x0);
    
    Ts = x(1) + 288
    Ta = x(2) + 288
    
    hold on
    rectangle('Position',[Ts-0.05 Ta-0.05 0.1 0.1],'Curvature',[1 1],'FaceColor',[1 0 0],'EdgeColor','k','LineWidth',2)
    
    posTs(tloop) = Ts;
    posTa(tloop) = Ta;
    
    plot(posTs,posTa,'k','LineWidth',2);
    hold off
    
    text(287.5,250.5,strcat('Date = ',num2str(date)),'FontSize',24)
    box on
    xlabel('Surface Temperature (oC)','FontSize',24)
    ylabel('Atmosphere Temperature (oC)','FontSize',24)
    
    hh = figure(1);
    pause(0.01)
    if mov_flag == 1
        frame = getframe(hh);
        writeVideo(aviobj,frame);
    end
    
end     % end tloop

if mov_flag == 1
    close(aviobj);
end

    function F = root2d(xp)   % Energy fluxes 
        
        x = xp + 288;
        feedfac = 0.001;      % feedback parameter 
        
        apa = apa0 + feedfac*(x(2)-248) + Delta;  % Changes in the atmospheric blanket
        tpa = tpa0 - feedfac*(x(2)-248) - Delta;
        as = as0 - feedfac*(x(1)-289);
        
        F(1) = c*(x(1)-x(2)) + sig*(1-apa)*x(1).^4 - sig*x(2).^4 - ta*(1-as)*Solar/4;
        F(2) = c*(x(1)-x(2)) + sig*(1-tpa - apa)*x(1).^4 - 2*sig*x(2).^4 + (1-aa0-ta+as*ta)*Solar/4;
        
    end

    function [x,y] = f5(X,Y)   % Dynamical flow equations
        
        k1 = 1/75;   % 75 year time constant for the Earth
        k2 = 1/25;   % 25 year time constant for the Atmosphere
        
        fun = @root2d;
        x0 = [0 0];
        x = fsolve(fun,x0);   % Solve for the temperatures that set the energy fluxes to zero
        
        Ts0 = x(1) + 288;   % Surface temperature in Kelvin
        Ta0 = x(2) + 288;   % Atmosphere temperature in Kelvin
        
        xtmp = -k1*(X - Ts0);   % Dynamical equations
        ytmp = -k2*(Y - Ta0);
        
        nrm = sqrt(xtmp.^2 + ytmp.^2);
        
        if smallarrow == 1
            x = xtmp./nrm;
            y = ytmp./nrm;
        else
            x = xtmp;
            y = ytmp;
        end
        
    end     % end f5

end       % end flowatmos

This model has a lot of parameters that can be tweaked. In addition to the parameters in the Table, the time dependence on the blanket properties of the atmosphere are governed by Delta0 and by feedfac for feedback of temperature on the atmosphere, such as increasing cloud cover and decrease ice cover. As an exercise, and using only small changes in the given parameters, find the following cases: 1) An increasing surface temperature is moderated by a falling atmosphere temperature; 2) The Earth goes into thermal run-away and ends like Venus; 3) The Earth initially warms then plummets into an ice age.

By David D. Nolte Oct. 16, 2022

References

[1] D. D. Nolte, Introduction to Modern Dynamics: Chaos, Networks, Space and Time, 2nd Ed. (Oxford University Press, 2019)

[2] E. Boeker and R. van Grondelle, Environmental Physics (Wiley, 1995)

[3] Recent lecture at the National Academy of Engineering by John Holdren.

by David D. Nolte

Is There a Quantum Trajectory?

Heisenberg’s uncertainty principle is a law of physics – it cannot be violated under any circumstances, no matter how much we may want it to yield or how hard we try to bend it.  Heisenberg, as he developed his ideas after his lone epiphany like a monk on the isolated island of Helgoland off the north coast of Germany in 1925, became a bit of a zealot, like a religious convert, convinced that all we can say about reality is a measurement outcome.  In his view, there was no independent existence of an electron other than what emerged from a measuring apparatus.  Reality, to Heisenberg, was just a list of numbers in a spread sheet—matrix elements.  He took this line of reasoning so far that he stated without exception that there could be no such thing as a trajectory in a quantum system.  When the great battle commenced between Heisenberg’s matrix mechanics against Schrödinger’s wave mechanics, Heisenberg was relentless, denying any reality to Schrödinger’s wavefunction other than as a calculation tool.  He was so strident that even Bohr, who was on Heisenberg’s side in the argument, advised Heisenberg to relent [1].  Eventually a compromise was struck, as Heisenberg’s uncertainty principle allowed Schrödinger’s wave functions to exist within limits—his uncertainty limits.

Disaster in the Poconos

Yet the idea of an actual trajectory of a quantum particle remained a type of heresy within the close quantum circles.  Years later in 1948, when a young Richard Feynman took the stage at a conference in the Poconos, he almost sabotaged his career in front of Bohr and Dirac—two of the giants who had invented quantum mechanics—by having the audacity to talk about particle trajectories in spacetime diagrams.

Feynman was making his first presentation of a new approach to quantum mechanics that he had developed based on path integrals. The challenge was that his method relied on space-time graphs in which “unphysical” things were allowed to occur.  In fact, unphysical things were required to occur, as part of the sum over many histories of his path integrals.  For instance, a key element in the approach was allowing electrons to travel backwards in time as positrons, or a process in which the electron and positron annihilate into a single photon, and then the photon decays back into an electron-positron pair—a process that is not allowed by mass and energy conservation.  But this is a possible history that must be added to Feynman’s sum.

It all looked like nonsense to the audience, and the talk quickly derailed.  Dirac pestered him with questions that he tried to deflect, but Dirac persisted like a raven.  A question was raised about the Pauli exclusion principle, about whether an orbital could have three electrons instead of the required two, and Feynman said that it could—all histories were possible and had to be summed over—an answer that dismayed the audience.  Finally, as Feynman was drawing another of his space-time graphs showing electrons as lines, Bohr rose to his feet and asked derisively whether Feynman had forgotten Heisenberg’s uncertainty principle that made it impossible to even talk about an electron trajectory.

It was hopeless.  The audience gave up and so did Feynman as the talk just fizzled out.  It was a disaster.  What had been meant to be Feynman’s crowning achievement and his entry to the highest levels of theoretical physics, had been a terrible embarrassment.  He slunk home to Cornell where he sank into one of his depressions.  At the close of the Pocono conference, Oppenheimer, the reigning king of physics, former head of the successful Manhattan Project and newly selected to head the prestigious Institute for Advanced Study at Princeton, had been thoroughly disappointed by Feynman.

But what Bohr and Dirac and Oppenheimer had failed to understand was that as long as the duration of unphysical processes was shorter than the energy differences involved, then it was literally obeying Heisenberg’s uncertainty principle.  Furthermore, Feynman’s trajectories—what became his famous “Feynman Diagrams”—were meant to be merely cartoons—a shorthand way to keep track of lots of different contributions to a scattering process.  The quantum processes certainly took place in space and time, conceptually like a trajectory, but only so far as time durations, and energy differences and locations and momentum changes were all within the bounds of the uncertainty principle.  Feynman had invented a bold new tool for quantum field theory, able to supply deep results quickly.  But no one at the Poconos could see it.

Fig. 1 The first Feynman diagram.

Coherent States

When Feynman had failed so miserably at the Pocono conference, he had taken the stage after Julian Schwinger, who had dazzled everyone with his perfectly scripted presentation of quantum field theory—the competing theory to Feynman’s.  Schwinger emerged the clear winner of the contest.  At that time, Roy Glauber (1925 – 2018) was a young physicist just taking his PhD from Schwinger at Harvard, and he later received a post-doc position at Princeton’s Institute for Advanced Study where he became part of a miniature revolution in quantum field theory that revolved around—not Schwinger’s difficult mathematics—but Feynman’s diagrammatic method.  So Feynman won in the end.  Glauber then went on to Caltech, where he filled in for Feynman’s lectures when Feynman was off in Brazil playing the bongos.  Glauber eventually returned to Harvard where he was already thinking about the quantum aspects of photons in 1956 when news of the photon correlations in the Hanbury-Brown Twiss (HBT) experiment were published.  Three years later, when the laser was invented, he began developing a theory of photon correlations in laser light that he suspected would be fundamentally different than in natural chaotic light. 

Because of his background in quantum field theory, and especially quantum electrodynamics, it was fairly easy to couch the quantum optical properties of coherent light in terms of Dirac’s creation and annihilation operators of the electromagnetic field. Glauber developed a “coherent state” operator that was a minimum uncertainty state of the quantized electromagnetic field, related to the minimum-uncertainty wave functions derived initially by Schrödinger in the late 1920’s. The coherent state represents a laser operating well above the lasing threshold and behaved as “the most classical” wavepacket that can be constructed.  Glauber was awarded the Nobel Prize in Physics in 2005 for his work on such “Glauber states” in quantum optics.

Fig. 2 Roy Glauber

Quantum Trajectories

Glauber’s coherent states are built up from the natural modes of a harmonic oscillator.  Therefore, it should come as no surprise that these coherent-state wavefunctions in a harmonic potential behave just like classical particles with well-defined trajectories. The quadratic potential matches the quadratic argument of the the Gaussian wavepacket, and the pulses propagate within the potential without broadening, as in Fig. 3, showing a snapshot of two wavepackets propagating in a two-dimensional harmonic potential. This is a somewhat radical situation, because most wavepackets in most potentials (or even in free space) broaden as they propagate. The quadratic potential is a special case that is generally not representative of how quantum systems behave.

Fig. 3 Harmonic potential in 2D and two examples of pairs of pulses propagating without broadening. The wavepackets in the center are oscillating in line, and the wavepackets on the right are orbiting the center of the potential in opposite directions. (Movies of the quantum trajectories can be viewed at Physics Unbound.)

To illustrate this special status for the quadratic potential, the wavepackets can be launched in a potential with a quartic perturbation. The quartic potential is anharmonic—the frequency of oscillation depends on the amplitude of oscillation unlike for the harmonic oscillator, where amplitude and frequency are independent. The quartic potential is integrable, like the harmonic oscillator, and there is no avenue for chaos in the classical analog. Nonetheless, wavepackets broaden as they propagate in the quartic potential, eventually spread out into a ring in the configuration space, as in Fig. 4.

Fig. 4 Potential with a quartic corrections. The initial gaussian pulses spread into a “ring” orbiting the center of the potential.

A potential with integrability has as many conserved quantities to the motion as there are degrees of freedom. Because the quartic potential is integrable, the quantum wavefunction may spread, but it remains highly regular, as in the “ring” that eventually forms over time. However, integrable potentials are the exception rather than the rule. Most potentials lead to nonintegrable motion that opens the door to chaos.

A classic (and classical) potential that exhibits chaos in a two-dimensional configuration space is the famous Henon-Heiles potential. This has a four-dimensional phase space which admits classical chaos. The potential has a three-fold symmetry which is one reason it is non-integral, since a particle must “decide” which way to go when it approaches a saddle point. In the quantum regime, wavepackets face the same decision, leading to a breakup of the wavepacket on top of a general broadening. This allows the wavefunction eventually to distribute across the entire configuration space, as in Fig. 5.

Fig. 5 The Henon-Heiles two-dimensional potential supports Hamiltonian chaos in the classical regime. In the quantum regime, the wavefunction spreads to eventually fill the accessible configuration space (for constant energy).

Youtube Video

Movies of quantum trajectories can be viewed at my Youtube Channel, Physics Unbound. The answer to the question “Is there a quantum trajectory?” can be seen visually as the movies run—they do exist in a very clear sense under special conditions, especially coherent states in a harmonic oscillator. And the concept of a quantum trajectory also carries over from a classical trajectory in cases when the classical motion is integrable, even in cases when the wavefunction spreads over time. However, for classical systems that display chaotic motion, wavefunctions that begin as coherent states break up into chaotic wavefunctions that fill the accessible configuration space for a given energy. The character of quantum evolution of coherent states—the most classical of quantum wavefunctions—in these cases reflects the underlying character of chaotic motion in the classical analogs. This process can be seen directly watching the movies as a wavepacket approaches a saddle point in the potential and is split. Successive splits of the multiple wavepackets as they interact with the saddle points is what eventually distributes the full wavefunction into its chaotic form.

Therefore, the idea of a “quantum trajectory”, so thoroughly dismissed by Heisenberg, remains a phenomenological guide that can help give insight into the behavior of quantum systems—both integrable and chaotic.

As a side note, the laws of quantum physics obey time-reversal symmetry just as the classical equations do. In the third movie of “A Quantum Ballet“, wavefunctions in a double-well potential are tracked in time as they start from coherent states that break up into chaotic wavefunctions. It is like watching entropy in action as an ordered state devolves into a disordered state. But at the half-way point of the movie, the imaginary part of the wavefunction has its sign flipped, and the dynamics continue. But now the wavefunctions move from disorder into an ordered state, seemingly going against the second law of thermodynamics. Flipping the sign of the imaginary part of the wavefunction at just one instant in time plays the role of a time-reversal operation, and there is no violation of the second law.

By David D. Nolte, Sept. 4, 2022

YouTube Video

YouTube Video of Quantum Trajectories

For more on the history of quantum trajectories, see Galileo Unbound from Oxford Press:

Order from Amazon

References

[1] See Chapter 8 , On the Quantum Footpath, in Galileo Unbound, D. D. Nolte (Oxford University Press, 2018)

[2] J. R. Nagel, A Review and Application of the Finite-Difference Time-Domain Algorithm Applied to the Schrödinger Equation, ACES Journal, Vol. 24, NO. 1, pp. 1-8 (2009)

by David D. Nolte

The Physics of Authoritarianism: The New World Order

An old joke goes that Democracy is a terrible form of government … except it’s better than all the others!

Our world today is faced with conflict between democracy and dictatorship. On the one side is the free world, where leaders are chosen by some form of representation of large numbers of citizens and sometimes even a majority. On the other side is authoritarianism where a select few are selected by a select few to govern everyone else.

[I]t has been said that democracy is the worst form of Government except all those other forms that have been tried from time to time; but there is the broad feeling in our country that the people should rule, and that public opinion expressed by all constitutional means, should shape, guide, and control the actions of Ministers who are their servants and not their masters.

Winston Churchill (1947)

An argument in favor of democracy is freedom of choice for the largest segment of the population, plus the ability to remove leaders who fail to provide for the perceived welfare of the most citizens. This makes democracy adaptive, shifting with the times. It also makes leaders accountable for their actions and crimes. An argument in favor of authoritarianism is the myth of the benevolent dictator–someone who knows what’s best for the people even if the people don’t know it themselves.

But dictators are rarely benevolent, and as they become saturated with power, they are corrupted. The criminal massacres, perpetrated by Putin, of Ukrainian civilians is one of the strongest recent arguments against authoritarianism. A single man decides, on a whim, the life and death of thousands or maybe more. The invasion of Ukraine is so egregious and unwarranted, that we wonder how the Russian people can put up with their isolated and manic leader. Yet by some measure more than 60% of the people in Russia approve of the war.

How can the free world see the invasion as the atrocity it is, while Russia’s majority sees it as a just war? The answer is a surprising result of population dynamics known as the replicator-mutator equation. The challenge for us here in the free world is to learn how to game the replicator-mutator equation to break up the monopoly of popular opinion and make Putin pay for his arrogance. This blog explains how “mass hysteria” can arise from forces within a complex environment, and how to construct a possible antidote.

Replicator-Mutator Equation

There are several simple models of population dynamics that try to explain the rise and fall of the number of individuals that belong to varying cohorts within the population. These models incorporate aspects of relative benefit of one group over another, plus the chance to change sides–defection. The dynamics under these conditions can be highly nonlinear and highly non-intuitive. One of the simplest of these models is known as the replicator-mutator model where replication follows the fitness of the cohort, and where individuals can defect to a “more fit” cohort.

The basic dynamics of the model are

where xa is the fraction of the population that is in cohort a, Wab is a transition probability, and φ is the average fitness of the full population. The transition matrix is given by

where fb is the fitness of cohort b and Qba is a stochastic matrix that allows for defection of an individual from one cohort to another. The fitness of a cohort is given by

where pbc is the pay-off matrix for the relative benefit of one cohort at the expense of another. Finally the average fitness is

The Einstein implicit summation convention is assumed in all of these equations, and the metric space in which the dynamics are embedded is “flat” so that there is no essential difference between superscripts and subscripts. There is also a conservation law that the sum over all population fractions equals unity.

In the language of population dynamics, this model has frequency-dependent fitness, with defection and pay-off, in a zero-sum game.

One of the simplest questions to answer with this model is how so many people can come to believe one thing. This is known as “opinion uniformity”.

Uniformity versus Diversity

This replicator-mutator model explains the property of opinion uniformity, as well as the opposite extreme of opinion diversity. The starting point for both is the pay-off matrix pbc which is assumed to be unity on the diagonal for b = c and to a constant factor a for b ~= c. This pay-off is symmetric so that all opinions are equally “believable”. The stochastic defection matrix is close to unity on the diagonal, and has random terms on the off-diagonal that are proportional to a constant ε. The defection matrix allows a person from one cohort to defect to the belief system of another cohort if they believe that the new cohort has more merit. Cohorts with greater merit (fitness) gain more members over time, while cohorts with lower merit have fewer members over time.

Note that the fitness increases with the number of members in the cohort. This is the bandwagon effect. A belief system is perceived to have more merit if there are more people who believe it. This clearly creates a positive feedback that would cause this cohort to grow. Even though all the cohorts have this same positive feedback, the zero-sum rule only allows one of the cohorts to grow to its maximum extent, taking members away from all the other cohorts. This is illustrated in Fig. 1. One belief system wins, taking almost the full population with it.

Fig. 1 Population fractions evolving as a function of time for a = 0.5 and a small defection rate ε = 0.02. One winner takes almost all the population. These are two views of the same data on semilog and log-log.

What allows the winner to take all is the positive feedback where the fitness of the cohort increases with the number of members, combined with the ability for that cohort to take members from other cohorts through the defection matrix.

However, all of the cohorts are trying the same thing, and the pay-off matrix is fully symmetric and equal for all cohorts, so no cohort is intrinsically “better” than another. This property opens the door to a strong alternative to opinion uniformity. In fact, as more members are allowed to defect, it creates a trend counter to winner-take-all, helping to equalize the cohorts. Suddenly, a bifurcation is passed when the winner-take-all converts discontinuously to a super-symmetric situation when all opinions are held by equal numbers of people. This is illustrated in Fig. 2 for a slightly higher defection rate ε = 0.03. The parameters are identical to those in Fig. 1, but the higher defection rate stabilizes the super-symmetric state of maximum diversity.

Fig. 2 Population fractions for higher defection rate of 0.03. In super-symmetric state, all opinions are held at the same rate with maximum diversity.

These two extreme results of the replicator-mutator equation, that switch suddenly from one to the other dependent on the defection rate, may seem to produce solutions neither of which are ideal for a healthy democracy. One the one hand, in the uniform case where the wining opinion is monolithic, everyone is a carbon-copy of everyone else, which is a form of cultural death (lack of diversity). But, on the other hand, one might argue that maximum opinion diversity is just as concerning, because no-one can agree on anything. If all opinions are equivalent, then everyone in the society believes something different and there is no common ground. But in the diversity case, at least there is no state-level control of the population. In the case of opinion uniformity, the wining opinion can be manipulated by propaganda.

The Propaganda Machine

A government can “seed” the belief networks with propaganda that favors the fitness of what they want their citizens to hear. Because of the positive feedback, any slight advantage of one opinion over others can allow that opinion to gain large numbers through the bandwagon effect. Of course, even stronger control that stifles dissent, for instance by shutting down the free press, makes it that much more likely that the state-controlled story is believed. This may be one reason for the 60% (as of the writing of this blog) support Putin’s war, despite the obvious lies that are being told. This is illustrated in Fig. 3 by boosting the payoff between two similar lies that the government wants its people to believe. These rise to take about 60% of the population. Members of the cohort are brain-washed, not by the government alone, but by all their neighbors who are parroting the same thing.

Fig. 3 Government propaganda acts as a “seed” that makes the propaganda grow faster than other beliefs, even for a defection rate of 0.03 which is above the threshold of Fig. 2.

Breaking the Monopoly of Thought

How do we fight back? Not just against the Kremlin’s propaganda, but also against QANON and Trump’s Big Lie and the pernicious fallacy of nationalism? The answer is simple: diversity of thought! The sliver bullet in the replicator-mutator model is the defection matrix. The existence of a bifurcation means that a relatively small increase in the amount of diverse opinion, and the freedom to swap opinions, can lead to a major qualitative collapse of the monolithic thought, even when supported by government propaganda, as shown in Fig. 4. More people may still believe in the state-supported propaganda than the others, but it is no longer a majority.

Fig. 4 Increasing the defection rate can help equalize free opinions against the state-supported propaganda

The above models were all very homogeneous. It is more realistic that people are connected through small-world networks. In this case, there is much more diversity, as shown in Fig. 5, although the defection rate needs to be much higher to prevent a monolithic opinion from dominating. The state-supported propaganda is buried in the resulting mix of diverse ideas. Therefore, to counteract state control, people must feel free to hop about in their choice of beliefs and have access to other beliefs.

Fig. 5 The defection matrix is multiplied by the adjacency matrix of a small-world network. There is significant diversity of thought, but a relatively high defection rate is needed. The state-supported propaganda is buried in this mix.

This is a bit paradoxical. On the one hand, the connectivity of the internet has fostered the rise of conspiracy theories and other odd-ball ideas. But sustained access to multiple sources of information is the best defense against all that crazy stuff winning out. In other words, not only do we have to put up with the lunatic fringe if we are to have full diversity of thought, but we need to encourage everyone to feel free to “shop around” for different ideas, even if some of them are crazy. Our free society shouldn’t be cancelling people who have divergent opinions, because that sets us down the path to authoritarianism. As a recent add said in the New York Times, “Cancel culture cancels culture.” Unfortunately, authoritarianism is on the rise around the world, and the US almost suffered that fate on Jan. 6, 2021. Furthermore, with Xi aligning with Putin and giving him the green light on Ukraine–cynically on the eve of the Olympic Games (of peace)–the new world order will revolve around that axis for decades to come, if the world survives that long. Diversity and freedom may be the only antidote.

By David D. Nolte, March 24, 2022

Matlab Program: Repmut.m

function repmut
% https://github.itap.purdue.edu/nolte/Matlab-Programs-for-Nonlinear-Dynamics

clear
format compact

N = 63;     
p = 0.5;

mutype = 1;     % 0 = Hamming   1 = rand
pay = 1;        % 0 = Hamming   1 = 1/sqrt(N) 
ep = 0.5;      % average mutation rate: 0.1 to 0.01 typical  (0.4835)

%%%%% Set original population
x0temp = rand(1,N);    % Initial population
sx = sum(x0temp);
y0 = x0temp/sx;
Pop0 = sum(y0);


%%%%% Set Adjacency

%node = makeglobal(N);
%node = makeER(N,0.25);       % 0.5     0.25 
%node = makeSF(N,6);       % 12         6
node = makeSW(N,7,0.125);   % 15,0.5    7,0.5
[Adj,degree,Lap] = adjacency(node);

%%%%%% Set Hamming distance
for yloop = 1:N
    for xloop = 1:N
        H(yloop,xloop) = hamming(yloop-1,xloop-1);
    end
end

%%%%%%% Set Mutation matrix
if mutype == 0
    Qtemp = 1./(1+H/ep);    %Mutation matrix on Hamming
    Qsum = sum(Qtemp,2);
    mnQsum = mean(Qsum);
    
    % Normalize mutation among species
    for yloop = 1:N
        for xloop = 1:N
            Q(yloop,xloop) = Qtemp(yloop,xloop)/Qsum(xloop);
        end
    end
    
elseif mutype == 1  
    S = stochasticmatrix(N);
    Stemp = S - diag(diag(S));
    Qtemp = ep*Stemp;
    sm = sum(Qtemp,2)';
    Q = Qtemp + diag(ones(1,N) - sm);
end

figure(1)
imagesc(Q)
title('Mutation Matrix')
colormap(jet)

%%%%%%% Set payoff matrix
if pay == 1
    payoff = zeros(N,N);
    for yloop = 1:N
        payoff(yloop,yloop) = 1;
        for xloop = yloop + 1:N
            payoff(yloop,xloop) = p;
            payoff(xloop,yloop) = p;
            payoff(1,N) = 1;    % Propaganda
            payoff(N,1) = 1;
        end
    end
elseif pay == 0
    payoff = zerodiag(exp(-1*H));
end

figure(2)
imagesc(payoff)
title('Payoff Matrix')
colormap(jet)

% Run time evolution
tspan = [0 4000];
[t,x] = ode45(@quasispec,tspan,y0);

Pop0
[sz,dum] = size(t);
Popend = sum(x(sz,:))

for loop = 1:N
    fit(loop) = sum(payoff(:,loop)'.*x(sz,:));
end

phistar = sum(fit.*x(sz,:))       % final average fitness

xend = x(sz,:)
sortxend = sort(xend,'descend');
coher = sum(sortxend(1:2))

figure(3)
clf
h = colormap(lines);
for loop = 1:N
    plot(t,x(:,loop),'Color',h(round(loop*64/N),:),'LineWidth',1.25)
    hold on
end
hold off

figure(4)
clf
for loop = 1:N
    semilogx(t,x(:,loop),'Color',h(round(loop*64/N),:),'LineWidth',1.25)
    hold on
end
hold off

figure(5)
clf
for loop = 1:N
    semilogy(t,x(:,loop),'Color',h(round(loop*64/N),:),'LineWidth',1.25)
    hold on
end
hold off

figure(6)
clf
for loop = 1:N
    loglog(t,x(:,loop),'Color',h(round(loop*64/N),:),'LineWidth',1.25)
    hold on
end
hold off

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%
%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
    function yd = quasispec(~,y)
        
        for floop = 1:N
            f(floop) = sum(payoff(:,floop).*y);
        end
        
        Connect = Adj + eye(N);
        
        % Transition matrix
        for yyloop = 1:N
            for xxloop = 1:N
                W(yyloop,xxloop) = f(yyloop)*(Connect(yyloop,xxloop)*Q(yyloop,xxloop));
            end
        end
        
        phi = sum(f'.*y);   % Average fitness of population
        
        yd = W*y - phi*y;
        
    end     % end quasispec
end

Further Reading

M. A. Nowak, Evolutionary Dynamics: Exploring the Equations of Life. Cambridge, Mass.: Harvard University Press, 2006.

by David D. Nolte

Spontaneous Symmetry Breaking: A Mechanical Model

Symmetry is the canvas upon which the laws of physics are written. Symmetry defines the invariants of dynamical systems. But when symmetry breaks, the laws of physics break with it, sometimes in dramatic fashion. Take the Big Bang, for example, when a highly-symmetric form of the vacuum, known as the “false vacuum”, suddenly relaxed to a lower symmetry, creating an inflationary cascade of energy that burst forth as our Universe.

The early universe was extremely hot and energetic, so much so that all the forces of nature acted as one–described by a unified Lagrangian (as yet resisting discovery by theoretical physicists) of the highest symmetry. Yet as the universe expanded and cooled, the symmetry of the Lagrangian broke, and the unified forces split into two (gravity and electro-nuclear). As the universe cooled further, the Lagrangian (of the Standard Model) lost more symmetry as the electro-nuclear split into the strong nuclear force and the electro-weak force. Finally, at a tiny fraction of a second after the Big Bang, the universe cooled enough that the unified electro-week force broke into the electromagnetic force and the weak nuclear force. At each stage, spontaneous symmetry breaking occurred, and invariants of physics were broken, splitting into new behavior. In 2008, Yoichiro Nambu received the Nobel Prize in physics for his model of spontaneous symmetry breaking in subatomic physics.

Fig. 1 The spontanous symmetry breaking cascade after the Big Bang. From Ref.

Bifurcation Physics

Physics is filled with examples of spontaneous symmetry breaking. Crystallization and phase transitions are common examples. When the temperature is lowered on a fluid of molecules with high average local symmetry, the molecular interactions can suddenly impose lower-symmetry constraints on relative positions, and the liquid crystallizes into an ordered crystal. Even solid crystals can undergo a phase transition as one symmetry becomes energetically advantageous over another, and the crystal can change to a new symmetry.

In mechanics, any time a potential function evolves slowly with some parameter, it can start with one symmetry and evolve to another lower symmetry. The mechanical system governed by such a potential may undergo a discontinuous change in behavior.

In complex systems and chaos theory, sudden changes in behavior can be quite common as some parameter is changed continuously. These discontinuous changes in behavior, in response to a continuous change in a control parameter, is known as a bifurcation. There are many types of bifurcation, carrying descriptive names like the pitchfork bifurcation, period-doubling bifurcation, Hopf bifurcation, and fold bifurcation, among others. The pitchfork bifurcation is a typical example, shown in Fig. 2. As a parameter is changed continuously (horizontal axis), a stable fixed point suddenly becomes unstable and two new stable fixed points emerge at the same time. This type of bifurcation is called pitchfork because the diagram looks like a three-tined pitchfork. (This is technically called a supercritical pitchfork bifurcation. In a subcritical pitchfork bifurcation the solid and dashed lines are swapped.) This is exactly the bifurcation displayed by a simple mechanical model that illustrates spontaneous symmetry breaking.

Fig. 2 Bifurcation plot of a pitchfork bifurcation. As a parameter is changed smoothly and continuously (horizontal axis), a stable fixed point suddenly splits into three fixed points: one unstable and the other two stable.

Sliding Mass on a Rotating Hoop

One of the simplest mechanical models that displays spontaneous symmetry breaking and the pitchfork bifurcation is a bead sliding without friction on a circular hoop that is spinning on the vertical axis, as in Fig. 3. When it spins very slowly, this is just a simple pendulum with a stable equilibrium at the bottom, and it oscillates with a natural oscillation frequency ω0 = sqrt(g/b), where b is the radius of the hoop and g is the acceleration due to gravity. On the other hand, when it spins very fast, then the bead is flung to to one side or the other by centrifugal force. The bead then oscillates around one of the two new stable fixed points, but the fixed point at the bottom of the hoop is very unstable, because any deviation to one side or the other will cause the centrifugal force to kick in. (Note that in the body frame, centrifugal force is a non-inertial force that arises in the non-inertial coordinate frame. )

Fig. 3 A bead sliding without friction on a circular hoop rotating about a vertical axis. At high speed, the bead has a stable equilibrium to either side of the vertical.

The solution uses the Euler equations for the body frame along principal axes. In order to use the standard definitions of ω1, ω2, and ω3, the angle θ MUST be rotated around the x-axis.  This means the x-axis points out of the page in the diagram.  The y-axis is tilted up from horizontal by θ, and the z-axis is tilted from vertical by θ.  This establishes the body frame.

The components of the angular velocity are

And the moments of inertia are (assuming the bead is small)

There is only one Euler equation that is non-trivial. This is for the x-axis and the angle θ. The x-axis Euler equation is

and solving for the angular acceleration gives.

This is a harmonic oscillator with a “phase transition” that occurs as ω increases from zero.  At first the stable equilibrium is at the bottom.  But when ω passes a critical threshold, the equilibrium angle begins to increase to a finite angle set by the rotation speed.

This can only be real if  the magnitude of the argument is equal to or less than unity, which sets the critical threshold spin rate to make the system move to the new stable points to one side or the other for

which interestingly is the natural frequency of the non-rotating pendulum. Note that there are two equivalent angles (positive and negative), so this problem has a degeneracy. 

This is an example of a dynamical phase transition that leads to spontaneous symmetry breaking and a pitchfork bifurcation. By integrating the angular acceleration we can get the effective potential for the problem. One contribution to the potential is due to gravity. The other is centrifugal force. When combined and plotted in Fig. 4 for a family of values of the spin rate ω, a pitchfork emerges naturally by tracing the minima in the effective potential. The values of the new equilibrium angles are given in Fig. 2.

Fig. 4 Effective potential as a function of angle for a family of spin rates. At the transition spin rate, the effective potential is essentially flat with zero natural frequency. The pitchfork is the dashed green line.

Below the transition threshold for ω, the bottom of the hoop is the equilibrium position. To find the natural frequency of oscillation, expand the acceleration expression

For small oscillations the natural frequency is given by

As the effective potential gets flatter, the natural oscillation frequency decreases until it vanishes at the transition spin frequency. As the hoop spins even faster, the new equilibrium positions emerge. To find the natural frequency of the new equilibria, expand θ around the new equilibrium θ’ = θ – θ0

Which is a harmonic oscillator with oscillation angular frequency

Note that this is zero frequency at the transition threshold, then rises to match the spin rate of the hoop at high frequency. The natural oscillation frequency as a function of the spin looks like Fig. 5.

Fig. 5 Angular oscillation frequency for the bead. The bifurcation occurs at the critical spin rate ω = sqrt(g/b).

This mechanical analog is highly relevant for the spontaneous symmetry breaking that occurs in ferroelectric crystals when they go through a ferroelectric transition. At high temperature, these crystals have no internal polarization. But as the crystal cools towards the ferroelectric transition temperature, the optical-mode phonon modes “soften” as the phonon frequency decreases and vanishes at the transition temperature when the crystal spontaneously polarizes in one of several equivalent directions. The observation of mode softening in a polar crystal is one signature of an impending ferroelectric phase transition. Our mass on the hoop captures this qualitative physics nicely.

Golden Behavior

For fun, let’s find at what spin frequency the harmonic oscillation frequency at the dynamic equilibria equal the original natural frequency of the pendulum. Then

which is the golden ratio.  It’s spooky how often the golden ratio appears in random physics problems!

This Blog Post is a Companion to the textbook Introduction to Modern Dynamics: Chaos, Networks, Space and Time, 2nd ed. (Oxford, 2019) that introduces topics of classical dynamics, Lagrangians and Hamiltonians, chaos theory, complex systems, synchronization, neural networks, econophysics and Special and General Relativity.

by David D. Nolte

A Random Walk in 10 Dimensions

Physics in high dimensions is becoming the norm in modern dynamics.  It is not only that string theory operates in ten dimensions (plus one for time), but virtually every complex dynamical system is described and analyzed within state spaces of high dimensionality.  Population dynamics, for instance, may describe hundreds or thousands of different species, each of whose time-varying populations define a separate axis in a high-dimensional space.  Coupled mechanical systems likewise may have hundreds or thousands (or more) of degrees of freedom that are described in high-dimensional phase space. 

In high-dimensional landscapes, mountain ridges are much more common than mountain peaks. This has profound consequences for the evolution of life, the dynamics of complex systems, and the power of machine learning.

For these reasons, as physics students today are being increasingly exposed to the challenges and problems of high-dimensional dynamics, it is important to build tools they can use to give them an intuitive feeling for the highly unintuitive behavior of systems in high-D.

Within the rapidly-developing field of machine learning, which often deals with landscapes (loss functions or objective functions) in high dimensions that need to be minimized, high dimensions are usually referred to in the negative as “The Curse of Dimensionality”.

Dimensionality might be viewed as a curse for several reasons.  First, it is almost impossible to visualize data in dimensions higher than d = 4 (the fourth dimension can sometimes be visualized using colors or time series).  Second, too many degrees of freedom create too many variables to fit or model, leading to the classic problem of overfitting.  Put simply, there is an absurdly large amount of room in high dimensions.  Third, our intuition about relationships among areas and volumes are highly biased by our low-dimensional 3D experiences, causing us to have serious misconceptions about geometric objects in high-dimensional spaces.  Physical processes occurring in 3D can be over-generalized to give preconceived notions that just don’t hold true in higher dimensions.

Take, for example, the random walk.  It is usually taught starting from a 1-dimensional random walk (flipping a coin) that is then extended to 2D and then to 3D…most textbooks stopping there.  But random walks in high dimensions are the rule rather than the exception in complex systems.  One example that is especially important in this context is the problem of molecular evolution.  Each site on a genome represents an independent degree of freedom, and molecular evolution can be described as a random walk through that space, but the space of all possible genetic mutations is enormous.  Faced with such an astronomically large set of permutations, it is difficult to conceive of how random mutations could possibly create something as complex as, say, ATP synthase which is the basis of all higher bioenergetics.  Fortunately, the answer to this puzzle lies in the physics of random walks in high dimensions. 

Why Ten Dimensions?

This blog presents the physics of random walks in 10 dimensions.  Actually, there is nothing special about 10 dimensions versus 9 or 11 or 20, but it gives a convenient demonstration of high-dimensional physics for several reasons.  First, it is high enough above our 3 dimensions that there is no hope to visualize it effectively, even by using projections, so it forces us to contend with the intrinsic “unvisualizability” of high dimensions.  Second, ten dimensions is just big enough that it behaves roughly like any higher dimension, at least when it comes to random walks.  Third, it is about as big as can be handled with typical memory sizes of computers.  For instance, a ten-dimensional hypercubic lattice with 10 discrete sites along each dimension has 10^10 lattice points (10 Billion or 10 Gigs) which is about the limit of what a typical computer can handle with internal memory.

As a starting point for visualization, let’s begin with the well-known 4D hypercube but extend it to a 4D hyperlattice with three values along each dimension instead of two. The resulting 4D lattice can be displayed in 2D as a network with 3^4 = 81 nodes and 216 links or edges. The result is shown in Fig. 1, represented in two dimensions as a network graph with nodes and edges. Each node has four links with neighbors. Despite the apparent 3D look that this graph has about it, if you look closely you will see the frustration that occurs when trying to link to 4 neighbors, causing many long-distance links.

[See YouTube video for movies showing evolving hyperlattices and random walks in 10D.]

Fig. 1 A 4D hyperlattice with three sites along each of the 4 dimensions. This high dimensional discrete lattice is represented as a network graph in 2D with nodes and edges.

We can also look at a 10D hypercube that has 2^10 = 1024 nodes and 5120 edges, shown in Fig. 2. It is a bit difficult to see the hypercubic symmetry when presented in 2D, but each node has exactly 10 links.

Fig. 2 A 10D hypercube of 1024 nodes and 5120 edges. Each node has exactly 10 links to neighbors

Extending this 10D lattice to 10 positions instead of 2 and trying to visualize it is prohibitive, since the resulting graph in 2D just looks like a mass of overlapping circles. However, our interest extends not just to ten locations per dimension, but to an unlimited number of locations. This is the 10D infinite lattice on which we want to explore the physics of the random walk.

Diffusion in Ten Dimensions

An unconstrained random walk in 10D is just a minimal extension beyond a simple random walk in 1D. Because each dimension is independent, a single random walker takes a random step along any of the 10 dimensions at each iteration so that motion in any one of the 10 dimensions is just a 1D random walk. Therefore, a simple way to visualize this random walk in 10D is simply to plot the walk against each dimension, as in Fig. 3. There is one chance in ten that the walker will take a positive or negative step along any given dimension at each time point.

Fig. 3 A single walker taking random unit steps in 10 dimensions. The position of the walker as a function of time is shown for all ten dimensions.

An alternate visualization of the 10D random walker is shown in Fig. 4 for the same data as Fig. 3. In this case the displacement is color coded, and each column is a different dimension. Time is on the vertical axis (starting at the top and increasing downward). This type of color map can easily be extended to hundreds of dimensions. Each row is a position vector of the single walker in the 10D space

Fig. 4 Same data as in Fig. 3 for a single 10D random walker on a hyperlattice. Distance is color coded. Time is on the vertical axis (increasing downward). Each row is a 10D position vector, and this representation is of a single 10D trajectory.

In the 10D hyperlattice in this section, all lattice sites are accessible at each time point, so there is no constraint preventing the walk from visiting a previously-visited node. There is a possible adjustment that can be made to the walk that prevents it from ever crossing its own path. This is known as a self-avoiding-walk (SAW). In two dimensions, there is a major difference in the geometric and dynamical properties of an ordinary walk and an SAW. However, in dimensions larger than 4, it turns out that there are so many possibilities of where to go (high-dimensional spaces have so much free room) that it is highly unlikely that a random walk will ever cross itself. Therefore, in our 10D hyperlattice we do not need to make the distinction between an ordinary walk and a self-avoiding-walk. However, there are other constraints that can be imposed that mimic how complex systems evolve in time, and these constraints can have important consequences, as we see next.

Random Walk in a Maximally Rough Landscape

In the infinite hyperlattice of the previous section, all lattice sites are the same and are all equally accessible. However, in the study of complex systems, it is common to assign a value to each node in a high-dimensional lattice. This value can be assigned by a potential function, producing a high-dimensional potential landscape over the lattice geometry. Or the value might be the survival fitness of a species, producing a high-dimensional fitness landscape that governs how species compete and evolve. Or the value might be a loss function (an objective function) in a minimization problem from multivariate analysis or machine learning. In all of these cases, the scalar value on the nodes defines a landscape over which a state point executes a walk. The question then becomes, what are the properties of a landscape in high dimensions, and how does it affect a random walker?

As an example, let’s consider a landscape that is completely random point-to-point. There are no correlations in this landscape, making it maximally rough. Then we require that a random walker takes a walk along iso-potentials in this landscape, never increasing and never decreasing its potential. Beginning with our spatial intuition living in 3D space, we might be concerned that such a walker would quickly get confined in some area of the lanscape. Think of a 2D topo map with countour lines drawn on it — If we start at a certain elevation on a mountain side, then if we must walk along directions that maintain our elevation, we stay on a given contour and eventually come back to our starting point after circling the mountain peak — we are trapped! But this intuition informed by our 3D lives is misleading. What happens in our 10D hyperlattice?

To make the example easy to analyze, let’s assume that our potential function is restricted to N discrete values. This means that of the 10 neighbors to a given walker site, on average only 10/N are likely to have the same potential value as the given walker site. This constrains the available sites for the walker, and it converts the uniform hyperlattice into a hyperlattice site percolation problem.

Percolation theory is a fascinating topic in statistical physics. There are many deep concepts that come from asking simple questions about how nodes are connected across a network. The most important aspect of percolation theory is the concept of a percolation threshold. Starting with a complete network that is connected end-to-end, start removing nodes at random. For some critical fraction of nodes removed (on average) there will no longer be a single connected cluster that spans the network. This critical fraction is known as the percolation threshold. Above the percolation threshold, a random walker can get from one part of the network to another. Below the percolation threshold, the random walker is confined to a local cluster.

If a hyperlattice has N discrete values for the landscape potential (or height, or contour) and if a random walker can only move to site that has the same value as the walker’s current value (remains on the level set), then only a fraction of the hyperlattice sites are available to the walker, and the question of whether the walker can find a path the spans the hyperlattice becomes simply a question of how the fraction of available sites relates to the percolation threshold.

The percolation threshold for hyperlattices is well known. For reasonably high dimensions, it is given to good accuracy by

where d is the dimension of the hyperlattice. For a 10D hyperlattice the percolation threshold is pc(10) = 0.0568, or about 6%. Therefore, if more than 6% of the sites of the hyperlattice have the same value as the walker’s current site, then the walker is free to roam about the hyperlattice.

If there are N = 5 discrete values for the potential, then 20% of the sites are available, which is above the percolation threshold, and walkers can go as far as they want. This statement holds true no matter what the starting value is. It might be 5, which means the walker is as high on the landscape as they can get. Or it might be 1, which means the walker is as low on the landscape as they can get. Yet even if they are at the top, if the available site fraction is above the percolation threshold, then the walker can stay on the high mountain ridge, spanning the landscape. The same is true if they start at the bottom of a valley. Therefore, mountain ridges are very common, as are deep valleys, yet they allow full mobility about the geography. On the other hand, a so-called mountain peak would be a 5 surrounded by 4’s or lower. The odds for having this happen in 10D are 0.2*(1-0.8^10) = 0.18. Then the total density of mountain peaks, in a 10D hyperlattice with 5 potential values, is only 18%. Therefore, mountain peaks are rare in 10D, while mountain ridges are common. In even higher dimensions, the percolation threshold decreases roughly inversely with the dimensionality, and mountain peaks become extremely rare and play virtually no part in walks about the landscape.

To illustrate this point, Fig. 5 is the same 10D network that is in Fig. 2, but only the nodes sharing the same value are shown for N = 5, which means that only 20% of the nodes are accessible to a walker who stays only on nodes with the same values. There is a “giant cluster” that remains connected, spanning the original network. If the original network is infinite, then the giant cluster is also infinite but contains a finite fraction of the nodes.

Fig. 5 A 10D cluster that spans the network in Fig. 2 for 1/5 of the nodes sharing the same landscape value. This cluster represents a mountain ridge that spans the space. There are four additional co-existing clusters, each of which separately spans the same 10D space.

The quantitative details of the random walk can change depending on the proximity of the sub-networks (the clusters, the ridges or the level sets) to the percolation threshold. For instance, a random walker in D =10 with N = 5 is shown in Fig. 6. The diffusion is a bit slower than in the unconstrained walk of Figs. 3 and 4. But the ability to wander about the 10D space is retained.

Fig. 6 A random walker on the level-set cluster of Fig. 5

This is then the general important result: In high-dimensional landscapes, mountain ridges are much more common than mountain peaks. This has profound consequences for the evolution of life, the dynamics of complex systems, and the power of machine learning.

Consequences for Evolution and Machine Learning

When the high-dimensional space is the space of possible mutations on a genome, and when the landscape is a fitness landscape that assigns a survival advantage for one mutation relative to others, then the random walk describes the evolution of a species across generations. The prevalence of ridges, or more generally level sets, in high dimensions has a major consequence for the evolutionary process, because a species can walk along a level set acquiring many possible mutations that have only neutral effects on the survivability of the species. At the same time, the genetic make-up is constantly drifting around in this “neutral network”, allowing the species’ genome to access distant parts of the space. Then, at some point, natural selection may tip the species up a nearby (but rare) peak, and a new equilibrium is attained for the species.

One of the early criticisms of fitness landscapes was the (erroneous) criticism that for a species to move from one fitness peak to another, it would have to go down and cross wide valleys of low fitness to get to another peak. But this was a left-over from thinking in 3D. In high-D, neutral networks are ubiquitous, and a mutation can take a step away from one fitness peak onto one of the neutral networks, which can be sampled by a random walk until the state is near some distant peak. It is no longer necessary to think in terms of high peaks and low valleys of fitness — just random walks. The evolution of extremely complex structures, like ATP synthase, can then be understood as a random walk along networks of nearly-neutral fitness — once our 3D biases are eliminated.

The same arguments hold for many situations in machine learning and especially deep learning. When training a deep neural network, there can be thousands of neural weights that need to be trained through the minimization of a loss function, also known as an objective function. The loss function is the equivalent to a potential, and minimizing the loss function over the thousands of dimensions is the same problem as maximizing the fitness of an evolving species.

At first look, one might think that deep learning is doomed to failure. We have all learned, from the earliest days in calculus, that enough adjustable parameter can fit anything, but the fit is meaningless because it predicts nothing. Deep learning seems to be the worst example of this. How can fitting thousands of adjustable parameters be useful when the dimensionality of the optimization space is orders of magnitude larger than the degrees of freedom of the system being modeled?

The answer comes from the geometry of high dimensions. The prevalence of neutral networks in high dimensions gives lots of chances to escape local minima. In fact, local minima are actually rare in high dimensions, and when they do occur, there is a neutral network nearby onto which they can escape (if the effective temperature of the learning process is set sufficiently high). Therefore, despite the insanely large number of adjustable parameters, general solutions, that are meaningful and predictive, can be found by adding random walks around the objective landscape as a partial strategy in combination with gradient descent.

Given the superficial analogy of deep learning to the human mind, the geometry of random walks in ultra-high dimensions may partially explain our own intelligence and consciousness.

Biblography

S. Gravilet, Fitness Landscapes and the Origins of Species. Princeton University Press, 2004.

M. Kimura, The Neutral Theory of Molecular Evolution. Cambridge University Press, 1968.

YouTube Vlog on A Random Walk in 10 Dimensions

by David D. Nolte

Edward Lorenz’ Chaotic Butterfly

The butterfly effect is one of the most widely known principles of chaos theory. It has become a meme, propagating through popular culture in movies, books, TV shows and even casual conversation.

Can a butterfly flapping its wings in Florida send a hurricane to New York?

The origin of the butterfly effect is — not surprisingly — the image of a butterfly-like set of trajectories that was generated, in one of the first computer simulations of chaos theory, by Edward Lorenz.

Lorenz’ Butterfly

Excerpted from Galileo Unbound (Oxford, 2018) pg. 215

When Edward Lorenz (1917 – 2008) was a child, he memorized all perfect squares up to ten thousand.  This obvious interest in mathematics led him to a master’s degree in the subject at Harvard in 1940 under the supervision of Georg Birkhoff.  Lorenz’s master’s thesis was on an aspect of Riemannian geometry, but his foray into nonlinear dynamics was triggered by the intervention of World War II.  Only a few months before receiving his doctorate in mathematics from Harvard, the Japanese bombed Pearl Harbor. 

Lorenz left the PhD program at Harvard to join the United States Army Air Force to train as a weather forecaster in early 1942, and he took courses on forecasting and meteorology at MIT.  After receiving a second master’s degree, this time in meteorology, Lorenz was posted to Hawaii, then to Saipan and finally to Guam.  His area of expertise was in high-level winds, which were important for high-altitude bombing missions during the final months of the war in the Pacific.  After the Japanese surrender, Lorenz returned to MIT, where he continued his studies in meteorology, receiving his doctorate degree in 1948 with a thesis on the application of fluid dynamical equations to predict the motion of storms. 

One of Lorenz’ colleagues at MIT was Norbert Wiener (1894 – 1964), with whom he sometimes played chess during lunch at the faculty club.  Wiener had published his landmark book Cybernetics: Control and Communication in the Animal and Machine in 1949 which arose out of the apparently mundane problem of gunnery control during the Second World War.  As an abstract mathematician, Wiener attempted to apply his cybernetic theory to the complexities of weather, but he developed a theorem concerning nonlinear fluid dynamics which appeared to show that linear interpolation, of sufficient resolution, would suffice for weather forecasting, possibly even long-range forecasting.  Many on the meteorology faculty embraced this theorem because it fell in line with common practices of the day in which tomorrow’s weather was predicted using linear regression on measurements taken today.  However, Lorenz was skeptical, having acquired a detailed understanding of atmospheric energy cascades as larger vortices induced smaller vortices all the way down to the molecular level, dissipating as heat, and then all the way back up again as heat drove large-scale convection.  This was clearly not a system that would yield to linearization.  Therefore, Lorenz determined to solve nonlinear fluid dynamics models to test this conjecture.

Even with a computer in hand, the atmospheric equations needed to be simplified to make the calculations tractable.  Lorenz was more a scientist than an engineer, and more of a meteorologist than a forecaster.  He did not hesitate to make simplifying assumptions if they retained the correct phenomenological behavior, even if they no longer allowed for accurate weather predictions. 

He had simplified the number of atmospheric equations down to twelve.  Progress was good, and by 1961, he had completed a large initial numerical study.  He focused on nonperiodic solutions, which he suspected would deviate significantly from the predictions made by linear regression, and this hunch was vindicated by his numerical output.  One day, as he was testing his results, he decided to save time by starting the computations midway by using mid-point results from a previous run as initial conditions.  He typed in the three-digit numbers from a paper printout and went down the hall for a cup of coffee.  When he returned, he looked at the printout of the twelve variables and was disappointed to find that they were not related to the previous full-time run.  He immediately suspected a faulty vacuum tube, as often happened.  But as he looked closer at the numbers, he realized that, at first, they tracked very well with the original run, but then began to diverge more and more rapidly until they lost all connection with the first-run numbers.  His initial conditions were correct to a part in a thousand, but this small error was magnified exponentially as the solution progressed.

At this point, Lorenz recalled that he “became rather excited”.  He was looking at a complete breakdown of predictability in atmospheric science.  If radically different behavior arose from the smallest errors, then no measurements would ever be accurate enough to be useful for long-range forecasting.  At a more fundamental level, this was a break with a long-standing tradition in science and engineering that clung to the belief that small differences produced small effects.  What Lorenz had discovered, instead, was that the deterministic solution to his 12 equations was exponentially sensitive to initial conditions (known today as SIC). 

The Lorenz Equations

Over the following months, he was able to show that SIC was a result of the nonperiodic solutions.  The more Lorenz became familiar with the behavior of his equations, the more he felt that the 12-dimensional trajectories had a repeatable shape.  He tried to visualize this shape, to get a sense of its character, but it is difficult to visualize things in twelve dimensions, and progress was slow.  Then Lorenz found that when the solution was nonperiodic (the necessary condition for SIC), four of the variables settled down to zero, leaving all the dynamics to the remaining three variables. 

Lorenz narrowed the equations of atmospheric instability down to three variables: the stream function, the change in temperature and the deviation in linear temperature. The only parameter in the stream function is something known as the Prandtl Number. This is a dimensionless number which is the ratio of the kinetic viscosity of the fluid to its thermal diffusion coefficient and is a physical property of the fluid. The only parameter in the change in temperature is the Rayleigh Number which is a dimensionless parameter proportional to the difference in temperature between the top and the bottom of the fluid layer. The final parameter, in the equation for the deviation in linear temperature, is the ratio of the height of the fluid layer to the width of the convection rolls. The final simplified model is given by the flow equations

The Butterfly

Lorenz finally had a 3-variable dynamical system that displayed chaos.  Moreover, it had a three-dimensional state space that could be visualized directly.  He ran his simulations, exploring the shape of the trajectories in three-dimensional state space for a wide range of initial conditions, and the trajectories did indeed always settle down to restricted regions of state space.  They relaxed in all cases to a sort of surface that was elegantly warped, with wing-like patterns like a butterfly, as the state point of the system followed its dynamics through time.  The attractor of the Lorenz equations was strange.  Later, in 1971, David Ruelle (1935 – ), a Belgian-French mathematical physicist named this a “strange attractor”, and this name has become a standard part of the language of the theory of chaos.

The first graphical representation of the butterfly attractor is shown in Fig. 1 drawn by Lorenz for his 1963 publication.

Fig. 1 Excerpts of the title, abstract and sections of Lorenz’ 1963 paper. His three-dimensional flow equations produce trajectories that relax onto a three-dimensional “strange attractor“.

Using our modern plotting ability, the 3D character of the butterfly is shown in Fig. 2

Fig. 2 Edward Lorenz’ chaotic butterfly

A projection onto the x-y plane is shown in Fig. 3. In the full 3D state space the trajectories never overlap, but in the projection onto a 2D plane the trajectories are moving above and below each other.

Fig. 3 Projection of the butterfly onto the x-y plane centered on the origin.

The reason it is called a strange attractor is because all initial conditions relax onto the strange attractor, yet every trajectory on the strange attractor separates exponentially from neighboring trajectories, displaying the classic SIC property of chaos. So here is an elegant collection of trajectories that are certainly not just random noise, yet detailed prediction is still impossible. Deterministic chaos has significant structure, and generates beautiful patterns, without actual “randomness”.

Python Program

#!/usr/bin/env python3
# -*- coding: utf-8 -*-
"""
Created on Mon Apr 16 07:38:57 2018

@author: nolte
Introduction to Modern Dynamics, 2nd edition (Oxford University Press, 2019)

Lorenz model of atmospheric turbulence
"""
import numpy as np
import matplotlib as mpl

import matplotlib.colors as colors
import matplotlib.cm as cmx

from scipy import integrate
from matplotlib import cm
from matplotlib import pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from matplotlib.colors import cnames
from matplotlib import animation

plt.close('all')

jet = cm = plt.get_cmap('jet') 
values = range(10)
cNorm  = colors.Normalize(vmin=0, vmax=values[-1])
scalarMap = cmx.ScalarMappable(norm=cNorm, cmap=jet)

def solve_lorenz(N=12, angle=0.0, max_time=8.0, sigma=10.0, beta=8./3, rho=28.0):

    fig = plt.figure()
    ax = fig.add_axes([0, 0, 1, 1], projection='3d')
    ax.axis('off')

    # prepare the axes limits
    ax.set_xlim((-25, 25))
    ax.set_ylim((-35, 35))
    ax.set_zlim((5, 55))

    def lorenz_deriv(x_y_z, t0, sigma=sigma, beta=beta, rho=rho):
        """Compute the time-derivative of a Lorenz system."""
        x, y, z = x_y_z
        return [sigma * (y - x), x * (rho - z) - y, x * y - beta * z]

    # Choose random starting points, uniformly distributed from -15 to 15
    np.random.seed(1)
    x0 = -10 + 20 * np.random.random((N, 3))

    # Solve for the trajectories
    t = np.linspace(0, max_time, int(500*max_time))
    x_t = np.asarray([integrate.odeint(lorenz_deriv, x0i, t)
                      for x0i in x0])

    # choose a different color for each trajectory
    # colors = plt.cm.viridis(np.linspace(0, 1, N))
    # colors = plt.cm.rainbow(np.linspace(0, 1, N))
    # colors = plt.cm.spectral(np.linspace(0, 1, N))
    colors = plt.cm.prism(np.linspace(0, 1, N))

    for i in range(N):
        x, y, z = x_t[i,:,:].T
        lines = ax.plot(x, y, z, '-', c=colors[i])
        plt.setp(lines, linewidth=1)

    ax.view_init(30, angle)
    plt.show()

    return t, x_t


t, x_t = solve_lorenz(angle=0, N=12)

plt.figure(2)
lines = plt.plot(t,x_t[1,:,0],t,x_t[1,:,1],t,x_t[1,:,2])
plt.setp(lines, linewidth=1)
lines = plt.plot(t,x_t[2,:,0],t,x_t[2,:,1],t,x_t[2,:,2])
plt.setp(lines, linewidth=1)
lines = plt.plot(t,x_t[10,:,0],t,x_t[10,:,1],t,x_t[10,:,2])
plt.setp(lines, linewidth=1)

To explore the parameter space of the Lorenz attractor, the key parameters to change are sigma (the Prandtl number), r (the Rayleigh number) and b on line 31 of the Python code.

References

[1] E. N. Lorenz, The essence of chaos (The Jessie and John Danz lectures; Jessie and John Danz lectures.). Seattle :: University of Washington Press (in English), 1993.

[2] E. N. Lorenz, “Deterministic Nonperiodic Flow,” Journal of the Atmospheric Sciences, vol. 20, no. 2, pp. 130-141, 1963 (1963)

The Physics of Life, the Universe and Everything:

Read more about the history of chaos theory in Galileo Unbound from Oxford University Press

Read Today.

by David D. Nolte

The Physics of U. S. Presidential Elections (why are so many elections so close?)

Well here is another squeaker! The 2020 U. S. presidential election was a dead heat. What is most striking is that half of the past six US presidential elections have been won by less than 1% of the votes cast in certain key battleground states. For instance, in 2000 the election was won in Florida by less than 1/100th of a percent of the total votes cast.

How can so many elections be so close? This question is especially intriguing when one considers the 2020 election, which should have been strongly asymmetric, because one of the two candidates had such serious character flaws. It is also surprising because the country is NOT split 50/50 between urban and rural populations (it’s more like 60/40). And the split of Democrat/Republican is about 33/29 — close, but not as close as the election. So how can the vote be so close so often? Is this a coincidence? Or something fundamental about our political system? The answer lies (partially) in nonlinear dynamics coupled with the libertarian tendencies of American voters.

Rabbits and Sheep

Elections are complex dynamical systems consisting of approximately 140 million degrees of freedom (the voters). Yet US elections are also surprisingly simple. They are dynamical systems with only 2 large political parties, and typically a very small third party.

Voters in a political party are not too different from species in an ecosystem. There are many population dynamics models of things like rabbit and sheep that seek to understand the steady-state solutions when two species vie for the same feedstock (or two parties vie for the same votes). Depending on reproduction rates and competition payoff, one species can often drive the other species to extinction. Yet with fairly small modifications of the model parameters, it is often possible to find a steady-state solution in which both species live in harmony. This is a symbiotic solution to the population dynamics, perhaps because the rabbits help fertilize the grass for the sheep to eat, and the sheep keep away predators for the rabbits.

There are two interesting features to such a symbiotic population-dynamics model. First, because there is a stable steady-state solution, if there is a perturbation of the populations, for instance if the rabbits are culled by the farmer, then the two populations will slowly relax back to the original steady-state solution. For this reason, this solution is called a “stable fixed point”. Deviations away from the steady-state values experience an effective “restoring force” that moves the population values back to the fixed point. The second feature of these models is that the steady state values depend on the parameters of the model. Small changes in the model parameters then cause small changes in the steady-state values. In this sense, this stable fixed point is not fundamental–it depends on the parameters of the model.

Fig. 1 Dynamics of rabbits and sheep competing for the same resource (grass). For these parameters, one species dies off while the other thrives. A slight shift in parameters can turn the central saddle point into a stable fixed point where sheep and rabbits coexist in stead state. ([1] Reprinted from Introduction to Modern Dynamics (Oxford University Press, 2019) pg. 119)

But there are dynamical models which do have a stability that maintains steady values even as the model parameters shift. These models have negative feedback, like many dynamical systems, but if the negative feedback is connected to winner-take-all outcomes of game theory, then a robustly stable fixed point can emerge at precisely the threshold where such a winner would take all.

The Replicator Equation

The replicator equation provides a simple model for competing populations [2]. Despite its simplicity, it can model surprisingly complex behavior. The central equation is a simple growth model

where the growth rate depends on the fitness fa of the a-th species relative to the average fitness φ of all the species. The fitness is given by

where pab is the payoff matrix among the different species (implicit Einstein summation applies). The fitness is frequency dependent through the dependence on xb. The average fitness is

This model has a zero-sum rule that keeps the total population constant. Therefore, a three-species dynamics can be represented on a two-dimensional “simplex” where the three vertices are the pure populations for each of the species. The replicator equation can be applied easily to a three-party system, one simply defines a payoff matrix that is used to define the fitness of a party relative to the others.

The Nonlinear Dynamics of Presidential Elections

Here we will consider the replicator equation with three political parties (Democratic, Republican and Libertarian). Even though the third party is never a serious contender, the extra degree of freedom provided by the third party helps to stabilize the dynamics between the Democrats and the Republicans.

It is already clear that an essentially symbiotic relationship is at play between Democrats and Republicans, because the elections are roughly 50/50. If this were not the case, then a winner-take-all dynamic would drive virtually everyone to one party or the other. Therefore, having 100% Democrats is actually unstable, as is 100% Republicans. When the populations get too far out of balance, they get too monolithic and too inflexible, then defections of members will occur to the other parties to rebalance the system. But this is just a general trend, not something that can explain the nearly perfect 50/50 vote of the 2020 election.

To create the ultra-stable fixed point at 50/50 requires an additional contribution to the replicator equation. This contribution must create a type of toggle switch that depends on the winner-take-all outcome of the election. If a Democrat wins 51% of the vote, they get 100% of the Oval Office. This extreme outcome then causes a back action on the electorate who is always afraid when one party gets too much power.

Therefore, there must be a shift in the payoff matrix when too many votes are going one way or the other. Because the winner-take-all threshold is at exactly 50% of the vote, this becomes an equilibrium point imposed by the payoff matrix. Deviations in the numbers of voters away from 50% causes a negative feedback that drives the steady-state populations back to 50/50. This means that the payoff matrix becomes a function of the number of voters of one party or the other. In the parlance of nonlinear dynamics, the payoff matrix becomes frequency dependent. This goes one step beyond the original replicator equation where it was the population fitness that was frequency dependent, but not the payoff matrix. Now the payoff matrix also becomes frequency dependent.

The frequency-dependent payoff matrix (in an extremely simple model of the election dynamics) takes on negative feedback between two of the species (here the Democrats and the Republicans). If these are the first and third species, then the payoff matrix becomes

where the feedback coefficient is

and where the population dependences on the off-diagonal terms guarantee that, as soon as one party gains an advantage, there is defection of voters to the other party. This establishes a 50/50 balance that is maintained even when the underlying parameters would predict a strongly asymmetric election.

For instance, look at the dynamics in Fig. 2. For this choice of parameters, the replicator model predicts a 75/25 win for the democrats. However, when the feedback is active, it forces the 50/50 outcome, despite the underlying advantage for the original parameters.

Fig. 2 Comparison of the stabilized election with 50/50 outcome compared to the replicator dynamics without the feedback. For the parameters chosen here, there would be a 75/25 victory of the Democrats over the Republications. However, when the feedback is in play, the votes balance out at 50/50.

There are several interesting features in this model. It may seem that the Libertarians are irrelevant because they never have many voters. But their presence plays a surprisingly important role. The Libertarians tend to stabilize the dynamics so that neither the democrats nor the republicans would get all the votes. Also, there is a saddle point not too far from the pure Libertarian vertex. That Libertarian vertex is an attractor in this model, so under some extreme conditions, this could become a one-party system…maybe not Libertarian in that case, but possibly something more nefarious, of which history can provide many sad examples. It’s a word of caution.

Disclaimers and Caveats

No attempt has been made to actually mode the US electorate. The parameters in the modified replicator equations are chosen purely for illustration purposes. This model illustrates a concept — that feedback in the payoff matrix can create an ultra-stable fixed point that is insensitive to changes in the underlying parameters of the model. This can possibly explain why so many of the US presidential elections are so tight.

Someone interested in doing actual modeling of US elections would need to modify the parameters to match known behavior of the voting registrations and voting records. The model presented here assumes a balanced negative feedback that ensures a 50/50 fixed point. This model is based on the aversion of voters to too much power in one party–an echo of the libertarian tradition in the country. A more sophisticated model would yield the fixed point as a consequence of the dynamics, rather than being a feature assumed in the model. In addition, nonlinearity could be added that would drive the vote off of the 50/50 point when the underlying parameters shift strongly enough. For instance, the 2008 election was not a close one, in part because the strong positive character of one of the candidates galvanized a large fraction of the electorate, driving the dynamics away from the 50/50 balance.

References

[1] D. D. Nolte, Introduction to Modern Dynamics: Chaos, Networks, Space and Time (Oxford University Press, 2019) 2nd Edition.

[2] Nowak, M. A. (2006). Evolutionary Dynamics: Exploring the Equations of Life. Cambridge, Mass., Harvard University Press.

by David D. Nolte

Physics in the Age of Contagion: Part 4. Fifty Shades of Immunity to COVID-19

This is the fourth installment in a series of blogs on the population dynamics of COVID-19. In my first blog I looked at a bifurcation physics model that held the possibility (and hope) that with sufficient preventive action the pandemic could have died out and spared millions. That hope was in vain.

What will it be like to live with COVID-19 as a constant factor of modern life for years to come?

In my second blog I looked at a two-component population dynamics model that showed the importance of locking down and not emerging too soon. It predicted that waiting only a few extra weeks before opening could have saved tens of thousands of lives. Unfortunately, because states like Texas and Florida opened too soon and refused to mandate the wearing of masks, thousands of lives were lost.

In my third blog I looked at a network physics model that showed the importance of rapid testing and contact tracing to remove infected individuals to push the infection rate low — not only to flatten the curve, but to drive it down. While most of the developed world is succeeding in achieving this, the United States is not.

In this fourth blog, I am looking at a simple mean-field model that shows what it will be like to live with COVID-19 as a constant factor of modern life for years to come. This is what will happen if the period of immunity to the disease is short and people who recover from the disease can get it again. Then the disease will never go away and the world will need to learn to deal with it. How different that world will look from the one we had just a year ago will depend on the degree of immunity that is acquired after infection, how long a vaccine will provide protection before booster shots are needed, and how many people will get the vaccine or will refus.

SIRS for SARS

COVID-19 is a SARS corona virus known as SARS-CoV-2. SARS stands for Severe Acute Respiratory Syndrome. There is a simple and well-established mean-field model for an infectious disease like SARS that infects individuals, from which they recover, but after some lag period they become susceptible again. This is called the SIRS model, standing for Susceptible-Infected-Recovered-Susceptible. This model is similar to the SIS model of my first blog, but it now includes a mean lifetime for the acquired immunity, after an individual recovers from the infection and then becomes susceptible again. The bifurcation threshold is the same for the SIRS model as the SIS model, but with SIRS there is a constant susceptible population. The mathematical flow equations for this model are

where i is the infected fraction, r is the recovered fraction, and 1 – i – r = s is the susceptible fraction. The infection rate for an individual who has k contacts is βk. The recovery rate is μ and the mean lifetime of acquired immunity after recovery is τlife = 1/ν. This model assumes that all individuals are equivalent (no predispositions) and there is no vaccine–only natural immunity that fades in time after recovery.

The population trajectories for this model are shown in Fig. 1. The figure on the left is a 3-simplex where every point in the triangle stands for a 3-tuple (i, r, s). Our own trajectory starts at the right bottom vertex and generates the green trajectory that spirals into the fixed point. The parameters are chosen to be roughly equivalent to what is known about the virus (but with big uncertainties in the model parameters). One of the key results is that the infection will oscillate over several years, settling into a steady state after about 4 years. Thereafter, there is a steady 3% infected population with 67% of the population susceptible and 30% recovered. The decay time for the immunity is assumed to be one year in this model. Note that the first peak in the infected numbers will be about 1 year, or around March 2021. There is a second smaller peak (the graph on the right is on a vertical log scale) at about 4 years, or sometime in 2024.

Fig. 1 SIRS model for COVID-19 in which immunity acquired after recovery fades in time so an individual can be infected again. If immunity fades and there is never a vaccine, a person will have an 80% chance of getting the virus at least twice in their lifetime, and COVID will become the third highest cause of death in the US after heart disease and cancer.

Although the recovered fraction is around 30% for these parameters, it is important to understand that this is a dynamic equilibrium. If there is no vaccine, then any individual who was once infected can be infected again after about a year. So if they don’t get the disease in the first year, they still have about a 4% chance to get it every following year. In 50 years, a 20-year-old today would have almost a 90% chance of having been infected at least once and an 80% chance of having gotten it at least twice. In other words, if there is never a vaccine, and if immunity fades after each recovery, then almost everyone will eventually get the disease several times in their lifetime. Furthermore, COVID will become the third most likely cause of death in the US after heart disease (first) and cancer (second). The sad part of this story is that it all could have been avoided if the government leaders of several key nations, along with their populations, had behaved responsibly.

The Asymmetry of Personal Cost under COVID

The nightly news in the US during the summer of 2020 shows endless videos of large parties, dense with people, mostly young, wearing no masks. This is actually understandable even though regrettable. It is because of the asymmetry of personal cost. Here is what that means …

On any given day, an individual who goes out and about in the US has only about a 0.01 percent chance of contracting the virus. In the entire year, there is only about a 3% chance that that individual will get the disease. And even if they get the virus, they only have a 2% chance of dying. So the actual danger per day per person is so minuscule that it is hard to understand why it is so necessary to wear a mask and socially distance. Therefore, if you go out and don’t wear a mask, almost nothing bad will happen to YOU. So why not? Why not screw the masks and just go out!

And this is why that’s such a bad idea: because if no-one wears a mask, then tens or hundreds of thousands of OTHERS will die.

This is the asymmetry of personal cost. By ignoring distancing, nothing is likely to happen to YOU, but thousands of OTHERS will die. How much of your own comfort are you willing to give up to save others? That is the existential question.

This year is the 75th anniversary of the end of WW II. During the war everyone rationed and recycled, not because they needed it for themselves, but because it was needed for the war effort. Almost no one hesitated back then. It was the right thing to do even though it cost personal comfort. There was a sense of community spirit and doing what was good for the country. Where is that spirit today? The COVID-19 pandemic is a war just as deadly as any war since WW II. There is a community need to battle it. All anyone has to do is wear a mask and behave responsibly. Is this such a high personal cost?

The Vaccine

All of this can change if a reliable vaccine can be developed. There is no guarantee that this can be done. For instance, there has never been a reliable vaccine for the common cold. A more sobering thought is to realize is that there has never been a vaccine for the closely related virus SARS-CoV-1 that broke out in 2003 in China but was less infectious. But the need is greater now, so there is reason for optimism that a vaccine can be developed that elicits the production of antibodies with a mean lifetime at least as long as for naturally-acquired immunity.

The SIRS model has the same bifurcation threshold as the SIS model that was discussed in a previous blog. If the infection rate can be made slower than the recovery rate, then the pandemic can be eliminated entirely. The threshold is

The parameter μ, the recovery rate, is intrinsic and cannot be changed. The parameter β, the infection rate per contact, can be reduced by personal hygiene and wearing masks. The parameter <k>, the average number of contacts to a susceptible person, can be significantly reduced by vaccinating a large fraction of the population.

To simulate the effect of vaccination, the average <k> per person can be reduced at the time of vaccination. This lowers the average infection rate. The results are shown in Fig. 2 for the original dynamics, a vaccination of 20% of the populace, and a vaccination of 40% of the populace. For 20% vaccination, the epidemic is still above threshold, although the long-time infection is lower. For 40% of the population vaccinated, the disease falls below threshold and would decay away and vanish.

Fig. 2 Vaccination at 52 weeks can lower the infection cases (20% vaccinated) or eliminate them entirely (40% vaccinated). The vaccinations would need booster shots every year (if the decay time of immunity is one year).

In this model, the vaccination is assumed to decay at the same rate as naturally acquired immunity (one year), so booster shots would be needed every year. Getting 40% of the population to get vaccinated may be achieved. Roughly that fraction get yearly flu shots in the US, so the COVID vaccine could be added to the list. But at 40% it would still be necessary for everyone to wear face masks and socially distance until the pandemic fades away. Interestingly, if the 40% got vaccinated all on the same date (across the world), then the pandemic would be gone in a few months. Unfortunately, that’s unrealistic, so with a world-wide push to get 40% of the World’s population vaccinated within five years, it would take that long to eliminate the disease, taking us to 2025 before we could go back to the way things were in November of 2019. But that would take a world-wide vaccination blitz the likes of which the world has never seen.

Python Code: SIRS.py

#!/usr/bin/env python3
# -*- coding: utf-8 -*-
"""
SIRS.py
Created on Fri July 17 2020
D. D. Nolte, "Introduction to Modern Dynamics: 
    Chaos, Networks, Space and Time, 2nd Edition (Oxford University Press, 2019)
@author: nolte
"""

import numpy as np
from scipy import integrate
from matplotlib import pyplot as plt

plt.close('all')

def tripartite(x,y,z):

    sm = x + y + z
    xp = x/sm
    yp = y/sm
    
    f = np.sqrt(3)/2
    
    y0 = f*xp
    x0 = -0.5*xp - yp + 1;
    
    lines = plt.plot(x0,y0)
    plt.setp(lines, linewidth=0.5)
    plt.plot([0, 1],[0, 0],'k',linewidth=1)
    plt.plot([0, 0.5],[0, f],'k',linewidth=1)
    plt.plot([1, 0.5],[0, f],'k',linewidth=1)
    plt.show()
    
print(' ')
print('SIRS.py')

def solve_flow(param,max_time=1000.0):

    def flow_deriv(x_y,tspan,mu,betap,nu):
        x, y = x_y
        
        return [-mu*x + betap*x*(1-x-y),mu*x-nu*y]
    
    x0 = [del1, del2]
    
    # Solve for the trajectories
    t = np.linspace(0, int(tlim), int(250*tlim))
    x_t = integrate.odeint(flow_deriv, x0, t, param)

    return t, x_t

 # rates per week
betap = 0.3;   # infection rate
mu = 0.2;      # recovery rate
nu = 0.02      # immunity decay rate

print('beta = ',betap)
print('mu = ',mu)
print('nu =',nu)
print('betap/mu = ',betap/mu)
          
del1 = 0.005         # initial infected
del2 = 0.005         # recovered

tlim = 600          # weeks (about 12 years)

param = (mu, betap, nu)    # flow parameters

t, y = solve_flow(param)
I = y[:,0]
R = y[:,1]
S = 1 - I - R

plt.figure(1)
lines = plt.semilogy(t,I,t,S,t,R)
plt.ylim([0.001,1])
plt.xlim([0,tlim])
plt.legend(('Infected','Susceptible','Recovered'))
plt.setp(lines, linewidth=0.5)
plt.xlabel('Days')
plt.ylabel('Fraction of Population')
plt.title('Population Dynamics for COVID-19')
plt.show()

plt.figure(2)
plt.hold(True)
for xloop in range(0,10):
    del1 = xloop/10.1 + 0.001
    del2 = 0.01

    tlim = 300
    param = (mu, betap, nu)    # flow parameters
    t, y = solve_flow(param)       
    I = y[:,0]
    R = y[:,1]
    S = 1 - I - R
    
    tripartite(I,R,S);

for yloop in range(1,6):
    del1 = 0.001;
    del2 = yloop/10.1
    t, y = solve_flow(param)
    I = y[:,0]
    R = y[:,1]
    S = 1 - I - R
    
    tripartite(I,R,S);
    
for loop in range(2,10):
    del1 = loop/10.1
    del2 = 1 - del1 - 0.01
    t, y = solve_flow(param)
    I = y[:,0]
    R = y[:,1]
    S = 1 - I - R
        
    tripartite(I,R,S);
    
plt.hold(False)
plt.title('Simplex Plot of COVID-19 Pop Dynamics')
 
vac = [1, 0.8, 0.6]
for loop in vac:
               
    # Run the epidemic to the first peak
    del1 = 0.005
    del2 = 0.005
    tlim = 52
    param = (mu, betap, nu)
    t1, y1 = solve_flow(param)
    
    # Now vaccinate a fraction of the population
    st = np.size(t1)
    del1 = y1[st-1,0]
    del2 = y1[st-1,1]
    tlim = 400
    
    param = (mu, loop*betap, nu)
    t2, y2 = solve_flow(param)
    
    t2 = t2 + t1[st-1]
    
    tc = np.concatenate((t1,t2))
    yc = np.concatenate((y1,y2))
    
    I = yc[:,0]
    R = yc[:,1]
    S = 1 - I - R
    
    plt.figure(3)
    plt.hold(True)
    lines = plt.semilogy(tc,I,tc,S,tc,R)
    plt.ylim([0.001,1])
    plt.xlim([0,tlim])
    plt.legend(('Infected','Susceptible','Recovered'))
    plt.setp(lines, linewidth=0.5)
    plt.xlabel('Weeks')
    plt.ylabel('Fraction of Population')
    plt.title('Vaccination at 1 Year')
    plt.show()
    
plt.hold(False)

Caveats and Disclaimers

No effort was made to match parameters to the actual properties of the COVID-19 pandemic. The SIRS model is extremely simplistic and can only show general trends because it homogenizes away all the important spatial heterogeneity of the disease across the cities and states of the country. If you live in a hot spot, this model says little about what you will experience locally. The decay of immunity is also a completely open question and the decay rate is completely unknown. It is easy to modify the Python program to explore the effects of differing decay rates and vaccination fractions. The model also can be viewed as a “compartment” to model local variations in parameters.