Tag / Henri Poincaré

by David D. Nolte

A Short History of Chaos Theory

Chaos seems to rule our world.  Weather events, natural disasters, economic volatility, empire building—all these contribute to the complexities that buffet our lives.  It is no wonder that ancient man attributed the chaos to the gods or to the fates, infinitely far from anything we can comprehend as cause and effect.  Yet there is a balm to soothe our wounds from the slings of life—Chaos Theory—if not to solve our problems, then at least to understand them.

(Sections of this Blog have been excerpted

from the book Galileo Unbound, published by Oxford University Press)

Chaos Theory is the theory of complex systems governed by multiple factors that produce complicated outputs.  The power of the theory is its ability recognize when the complicated outputs are not “random”, no matter how complicated they are, but are in fact determined by the inputs.  Furthermore, chaos theory finds structures and patterns within the output—like the fractal structures known as “strange attractors”.  These patterns not only are not random, but they tell us about the internal mechanics of the system, and they tell us where to look “on average” for the system behavior. 

In other words, chaos theory tames the chaos, and we no longer need to blame gods or the fates.

Henri Poincare (1889)

The first glimpse of the inner workings of chaos was made by accident when Henri Poincaré responded to a mathematics competition held in honor of the King of Sweden.  The challenge was to prove whether the solar system was absolutely stable, or whether there was a danger that one day the Earth would be flung from its orbit.  Poincaré had already been thinking about the stability of dynamical systems so he wrote up his solution to the challenge and sent it in, believing that he had indeed proven that the solar system was stable.

His entry to the competition was the most convincing, so he was awarded the prize and instructed to submit the manuscript for publication.  The paper was already at the printers and coming off the presses when Poincaré was asked by the competition organizer to check one last part of the proof which one of the reviewer’s had questioned relating to homoclinic orbits.

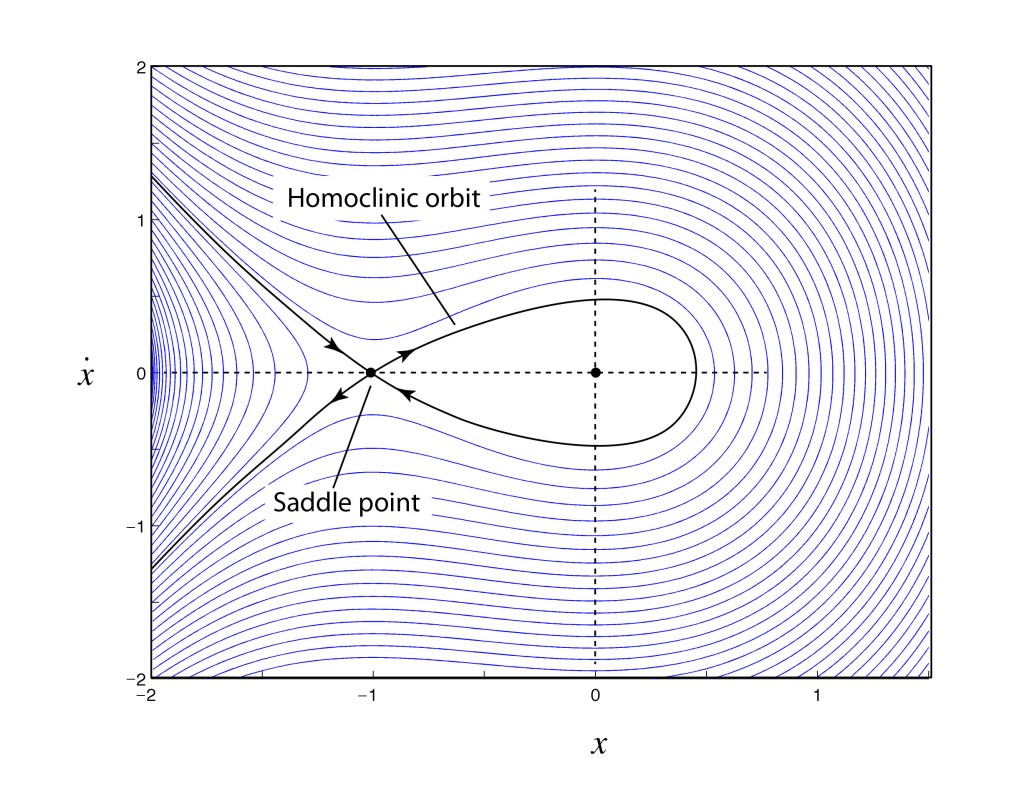
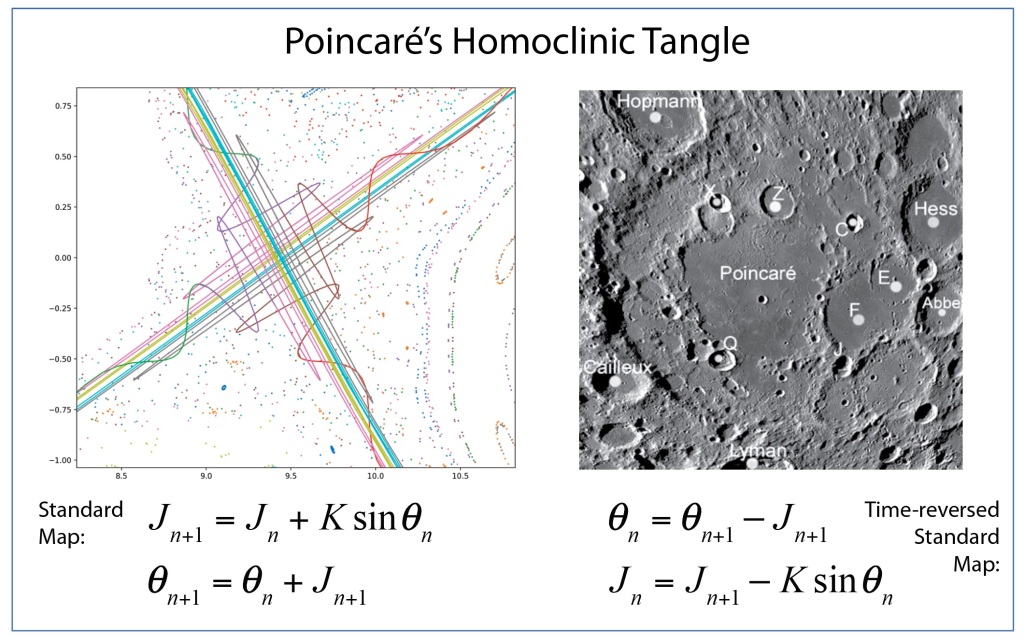
Fig. 1 A homoclinic orbit is an orbit in phase space that intersects itself.

To Poincaré’s horror, as he checked his results against the reviewer’s comments, he found that he had made a fundamental error, and in fact the solar system would never be stable.  The problem that he had overlooked had to do with the way that orbits can cross above or below each other on successive passes, leading to a tangle of orbital trajectories that crisscrossed each other in a fine mesh.  This is known as the “homoclinic tangle”: it was the first glimpse that deterministic systems could lead to unpredictable results. Most importantly, he had developed the first mathematical tools that would be needed to analyze chaotic systems—such as the Poincaré section—but nearly half a century would pass before these tools would be picked up again. 

Poincaré paid out of his own pocket for the first printing to be destroyed and for the corrected version of his manuscript to be printed in its place [1]. No-one but the competition organizers and reviewers ever saw his first version.  Yet it was when he was correcting his mistake that he stumbled on chaos for the first time, which is what posterity remembers him for. This little episode in the history of physics went undiscovered for a century before being brought to light by Barrow-Green in her 1997 book Poincaré and the Three Body Problem [2].

Fig. 2 Henri Poincaré’s homoclinic tangle from the Standard Map. (The picture on the right is the Poincaré crater on the moon). For more details, see my blog on Poincaré and his Homoclinic Tangle.

Cartwight and Littlewood (1945)

During World War II, self-oscillations and nonlinear dynamics became strategic topics for the war effort in England. High-power magnetrons were driving long-range radar, keeping Britain alert to Luftwaffe bombing raids, and the tricky dynamics of these oscillators could be represented as a driven van der Pol oscillator. These oscillators had been studied in the 1920’s by the Dutch physicist Balthasar van der Pol (1889–1959) when he was completing his PhD thesis at the University of Utrecht on the topic of radio transmission through ionized gases. van der Pol had built a short-wave triode oscillator to perform experiments on radio diffraction to compare with his theoretical calculations of radio transmission. Van der Pol’s triode oscillator was an engineering feat that produced the shortest wavelengths of the day, making van der Pol intimately familiar with the operation of the oscillator, and he proposed a general form of differential equation for the triode oscillator.

Fig. 3 Driven van der Pol oscillator equation.

Research on the radar magnetron led to theoretical work on driven nonlinear oscillators, including the discovery that a driven van der Pol oscillator could break up into wild and intermittent patterns. This “bad” behavior of the oscillator circuit (bad for radar applications) was the first discovery of chaotic behavior in man-made circuits.

These irregular properties of the driven van der Pol equation were studied by Mary- Lucy Cartwright (1990–1998) (the first woman to be elected a fellow of the Royal Society) and John Littlewood (1885–1977) at Cambridge who showed that the coexistence of two periodic solutions implied that discontinuously recurrent motion—in today’s parlance, chaos— could result, which was clearly undesirable for radar applications. The work of Cartwright and Littlewood [3] later inspired the work by Levinson and Smale as they introduced the field of nonlinear dynamics.

Fig. 4 Mary Cartwright

Andrey Kolmogorov (1954)

The passing of the Russian dictator Joseph Stalin provided a long-needed opening for Soviet scientists to travel again to international conferences where they could meet with their western colleagues to exchange ideas.  Four Russian mathematicians were allowed to attend the 1954 International Congress of Mathematics (ICM) held in Amsterdam, the Netherlands.  One of those was Andrey Nikolaevich Kolmogorov (1903 – 1987) who was asked to give the closing plenary speech.  Despite the isolation of Russia during the Soviet years before World War II and later during the Cold War, Kolmogorov was internationally renowned as one of the greatest mathematicians of his day.

By 1954, Kolmogorov’s interests had spread into topics in topology, turbulence and logic, but no one was prepared for the topic of his plenary lecture at the ICM in Amsterdam.  Kolmogorov spoke on the dusty old topic of Hamiltonian mechanics.  He even apologized at the start for speaking on such an old topic when everyone had expected him to speak on probability theory.  Yet, in the length of only half an hour he laid out a bold and brilliant outline to a proof that the three-body problem had an infinity of stable orbits.  Furthermore, these stable orbits provided impenetrable barriers to the diffusion of chaotic motion across the full phase space of the mechanical system. The crucial consequences of this short talk were lost on almost everyone who attended as they walked away after the lecture, but Kolmogorov had discovered a deep lattice structure that constrained the chaotic dynamics of the solar system.

Kolmogorov’s approach used a result from number theory that provides a measure of how close an irrational number is to a rational one.  This is an important question for orbital dynamics, because whenever the ratio of two orbital periods is a ratio of integers, especially when the integers are small, then the two bodies will be in a state of resonance, which was the fundamental source of chaos in Poincaré’s stability analysis of the three-body problem.    After Komogorov had boldly presented his results at the ICM of 1954 [4], what remained was the necessary mathematical proof of Kolmogorov’s daring conjecture.  This would be provided by one of his students, V. I. Arnold, a decade later.  But before the mathematicians could settle the issue, an atmospheric scientist, using one of the first electronic computers, rediscovered Poincaré’s tangle, this time in a simplified model of the atmosphere.

Edward Lorenz (1963)

In 1960, with the help of a friend at MIT, the atmospheric scientist Edward Lorenz purchased a Royal McBee LGP-30 tabletop computer to make calculation of a simplified model he had derived for the weather.  The McBee used 113 of the latest miniature vacuum tubes and also had 1450 of the new solid-state diodes made of semiconductors rather than tubes, which helped reduce the size further, as well as reducing heat generation.  The McBee had a clock rate of 120 kHz and operated on 31-bit numbers with a 15 kB memory.  Under full load it used 1500 Watts of power to run.  But even with a computer in hand, the atmospheric equations needed to be simplified to make the calculations tractable.  Lorenz simplified the number of atmospheric equations down to twelve, and he began programming his Royal McBee. 

Progress was good, and by 1961, he had completed a large initial numerical study.  One day, as he was testing his results, he decided to save time by starting the computations midway by using mid-point results from a previous run as initial conditions.  He typed in the three-digit numbers from a paper printout and went down the hall for a cup of coffee.  When he returned, he looked at the printout of the twelve variables and was disappointed to find that they were not related to the previous full-time run.  He immediately suspected a faulty vacuum tube, as often happened.  But as he looked closer at the numbers, he realized that, at first, they tracked very well with the original run, but then began to diverge more and more rapidly until they lost all connection with the first-run numbers.  The internal numbers of the McBee had a precision of 6 decimal points, but the printer only printed three to save time and paper.  His initial conditions were correct to a part in a thousand, but this small error was magnified exponentially as the solution progressed.  When he printed out the full six digits (the resolution limit for the machine), and used these as initial conditions, the original trajectory returned.  There was no mistake.  The McBee was working perfectly.

At this point, Lorenz recalled that he “became rather excited”.  He was looking at a complete breakdown of predictability in atmospheric science.  If radically different behavior arose from the smallest errors, then no measurements would ever be accurate enough to be useful for long-range forecasting.  At a more fundamental level, this was a break with a long-standing tradition in science and engineering that clung to the belief that small differences produced small effects.  What Lorenz had discovered, instead, was that the deterministic solution to his 12 equations was exponentially sensitive to initial conditions (known today as SIC). 

The more Lorenz became familiar with the behavior of his equations, the more he felt that the 12-dimensional trajectories had a repeatable shape.  He tried to visualize this shape, to get a sense of its character, but it is difficult to visualize things in twelve dimensions, and progress was slow, so he simplified his equations even further to three variables that could be represented in a three-dimensional graph [5]. 

Fig. 5 Two-dimensional projection of the three-dimensional Lorenz Butterfly.

V. I. Arnold (1964)

Meanwhile, back in Moscow, an energetic and creative young mathematics student knocked on Kolmogorov’s door looking for an advisor for his undergraduate thesis.  The youth was Vladimir Igorevich Arnold (1937 – 2010), who showed promise, so Kolmogorov took him on as his advisee.  They worked on the surprisingly complex properties of the mapping of a circle onto itself, which Arnold filed as his dissertation in 1959.  The circle map holds close similarities with the periodic orbits of the planets, and this problem led Arnold down a path that drew tantalizingly close to Kolmogorov’s conjecture on Hamiltonian stability.  Arnold continued in his PhD with Kolmogorov, solving Hilbert’s 13th problem by showing that every function of n variables can be represented by continuous functions of a single variable.  Arnold was appointed as an assistant in the Faculty of Mechanics and Mathematics at Moscow State University.

Arnold’s habilitation topic was Kolmogorov’s conjecture, and his approach used the same circle map that had played an important role in solving Hilbert’s 13th problem.  Kolmogorov neither encouraged nor discouraged Arnold to tackle his conjecture.  Arnold was led to it independently by the similarity of the stability problem with the problem of continuous functions.  In reference to his shift to this new topic for his habilitation, Arnold stated “The mysterious interrelations between different branches of mathematics with seemingly no connections are still an enigma for me.”  [6] 

Arnold began with the problem of attracting and repelling fixed points in the circle map and made a fundamental connection to the theory of invariant properties of action-angle variables .  These provided a key element in the proof of Kolmogorov’s conjecture.  In late 1961, Arnold submitted his results to the leading Soviet physics journal—which promptly rejected it because he used forbidden terms for the journal, such as “theorem” and “proof”, and he had used obscure terminology that would confuse their usual physicist readership, terminology such as “Lesbesgue measure”, “invariant tori” and “Diophantine conditions”.  Arnold withdrew the paper.

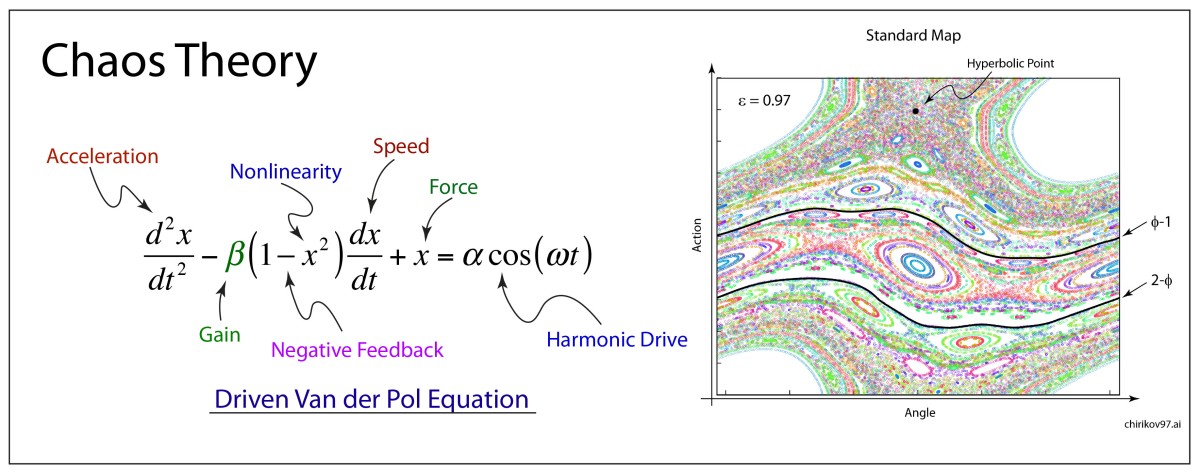
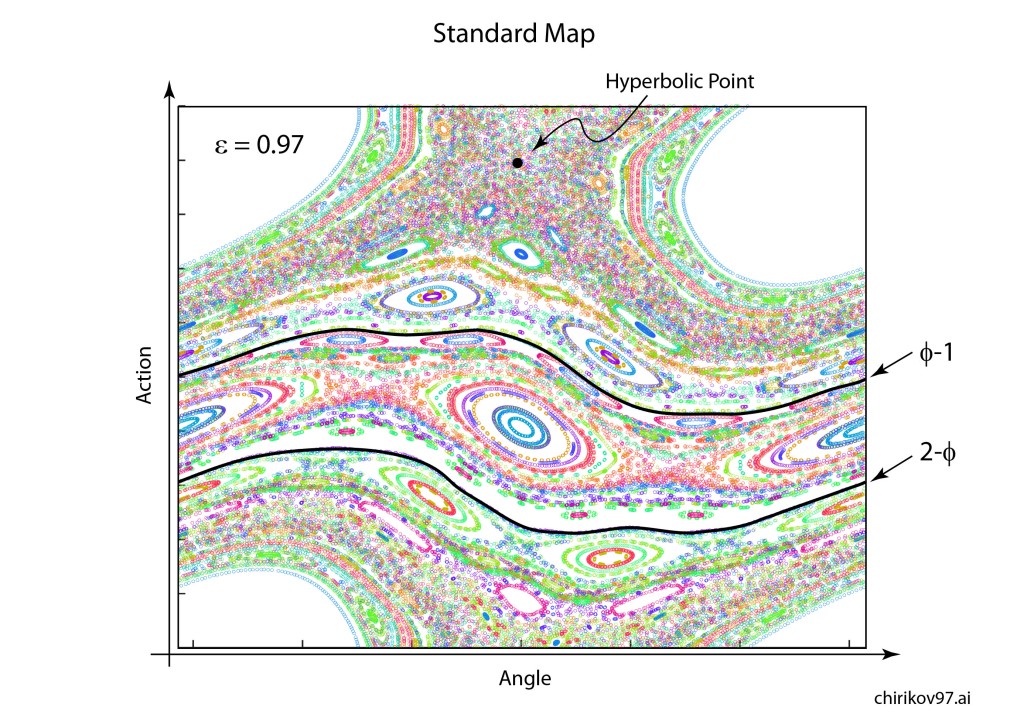
Arnold later incorporated an approach pioneered by Jurgen Moser [7] and published a definitive article on the problem of small divisors in 1963 [8].  The combined work of Kolmogorov, Arnold and Moser had finally established the stability of irrational orbits in the three-body problem, the most irrational and hence most stable orbit having the frequency of the golden mean.  The term “KAM theory”, using the first initials of the three theorists, was coined in 1968 by B. V. Chirikov, who also introduced in 1969 what has become known as the Chirikov map (also known as the Standard map ) that reduced the abstract circle maps of Arnold and Moser to simple iterated functions that any student can program easily on a computer to explore KAM invariant tori and the onset of Hamiltonian chaos, as in Fig. 1 [9]. 

Fig. 6 The Chirikov Standard Map when the last stable orbits are about to dissolve for ε = 0.97.

Sephen Smale (1967)

Stephen Smale was at the end of a post-graduate fellowship from the National Science Foundation when he went to Rio to work with Mauricio Peixoto.  Smale and Peixoto had met in Princeton in 1960 where Peixoto was working with Solomon Lefschetz  (1884 – 1972) who had an interest in oscillators that sustained their oscillations in the absence of a periodic force.  For instance, a pendulum clock driven by the steady force of a hanging weight is a self-sustained oscillator.  Lefschetz was building on work by the Russian Aleksandr A. Andronov (1901 – 1952) who worked in the secret science city of Gorky in the 1930’s on nonlinear self-oscillations using Poincaré’s first return map.  The map converted the continuous trajectories of dynamical systems into discrete numbers, simplifying problems of feedback and control. 

The central question of mechanical control systems, even self-oscillating systems, was how to attain stability.  By combining approaches of Poincaré and Lyapunov, as well as developing their own techniques, the Gorky school became world leaders in the theory and applications of nonlinear oscillations.  Andronov published a seminal textbook in 1937 The Theory of Oscillations with his colleagues Vitt and Khaykin, and Lefschetz had obtained and translated the book into English in 1947, introducing it to the West.  When Peixoto returned to Rio, his interest in nonlinear oscillations captured the imagination of Smale even though his main mathematical focus was on problems of topology.  On the beach in Rio, Smale had an idea that topology could help prove whether systems had a finite number of periodic points.  Peixoto had already proven this for two dimensions, but Smale wanted to find a more general proof for any number of dimensions.

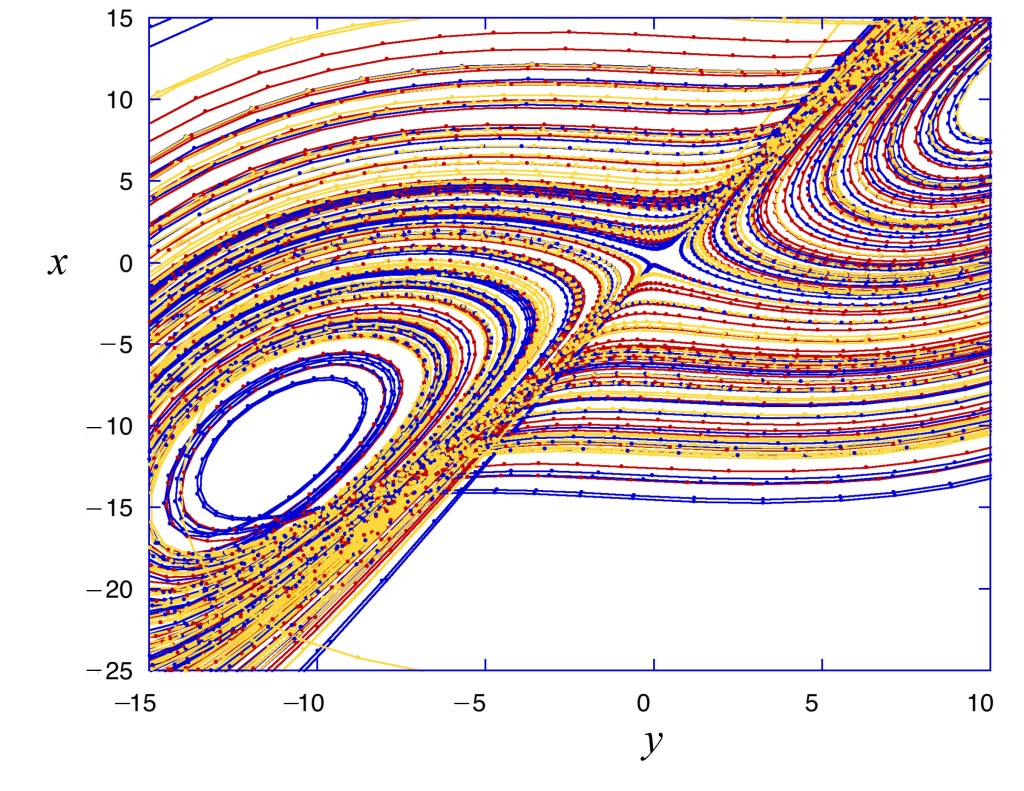
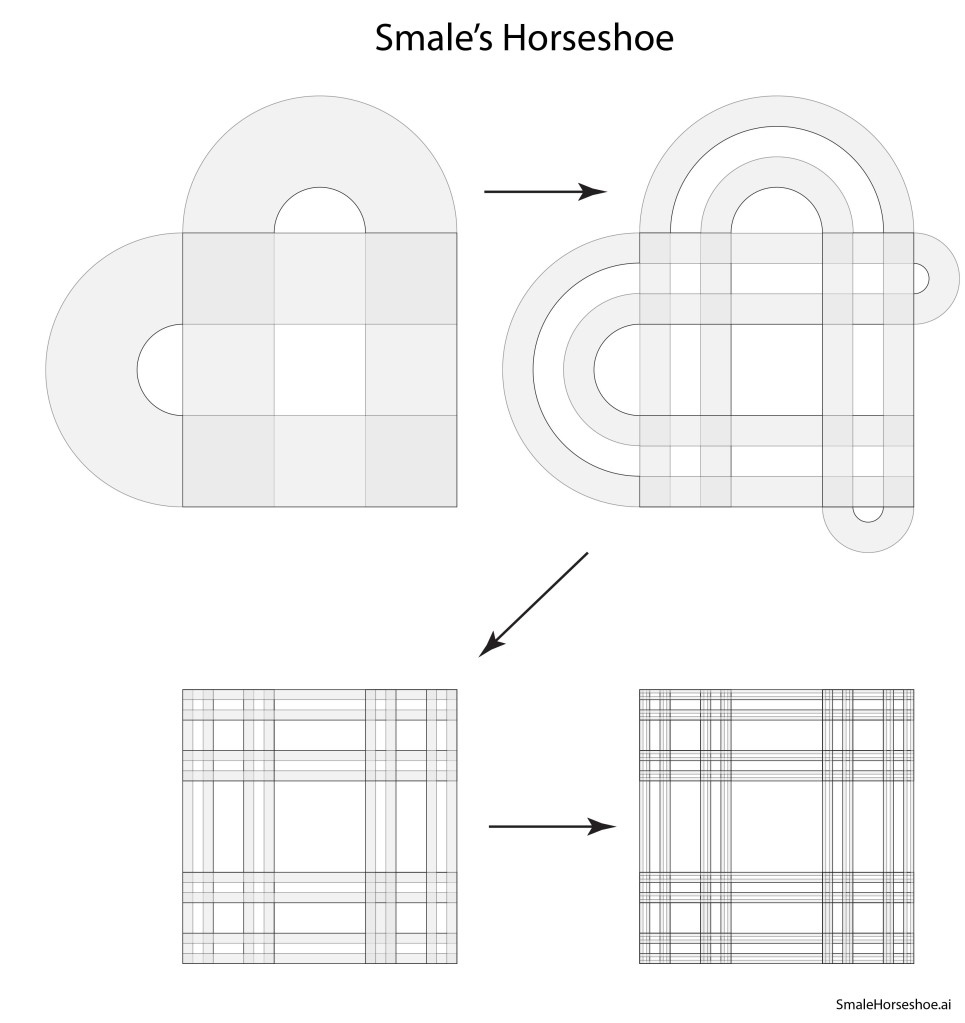
Norman Levinson (1912 – 1975) at MIT became aware of Smale’s interests and sent off a letter to Rio in which he suggested that Smale should look at Levinson’s work on the triode self-oscillator (a van der Pol oscillator), as well as the work of Cartwright and Littlewood who had discovered quasi-periodic behavior hidden within the equations.  Smale was puzzled but intrigued by Levinson’s paper that had no drawings or visualization aids, so he started scribbling curves on paper that bent back upon themselves in ways suggested by the van der Pol dynamics.  During a visit to Berkeley later that year, he presented his preliminary work, and a colleague suggested that the curves looked like strips that were being stretched and bent into a horseshoe. 

Smale latched onto this idea, realizing that the strips were being successively stretched and folded under the repeated transformation of the dynamical equations.  Furthermore, because dynamics can move forward in time as well as backwards, there was a sister set of horseshoes that were crossing the original set at right angles.  As the dynamics proceeded, these two sets of horseshoes were repeatedly stretched and folded across each other, creating an infinite latticework of intersections that had the properties of the Cantor set.  Here was solid proof that Smale’s original conjecture was wrong—the dynamics had an infinite number of periodicities, and they were nested in self-similar patterns in a latticework of points that map out a Cantor-like set of points.  In the two-dimensional case, shown in the figure, the fractal dimension of this lattice is D = ln4/ln3 = 1.26, somewhere in dimensionality between a line and a plane.  Smale’s infinitely nested set of periodic points was the same tangle of points that Poincaré had noticed while he was correcting his King Otto Prize manuscript.  Smale, using modern principles of topology, was finally able to put rigorous mathematical structure to Poincaré’s homoclinic tangle. Coincidentally, Poincaré had launched the modern field of topology, so in a sense he sowed the seeds to the solution to his own problem.

Fig. 7 The horseshoe takes regions of phase space and stretches and folds them over and over to create a lattice of overlapping trajectories.

Ruelle and Takens (1971)

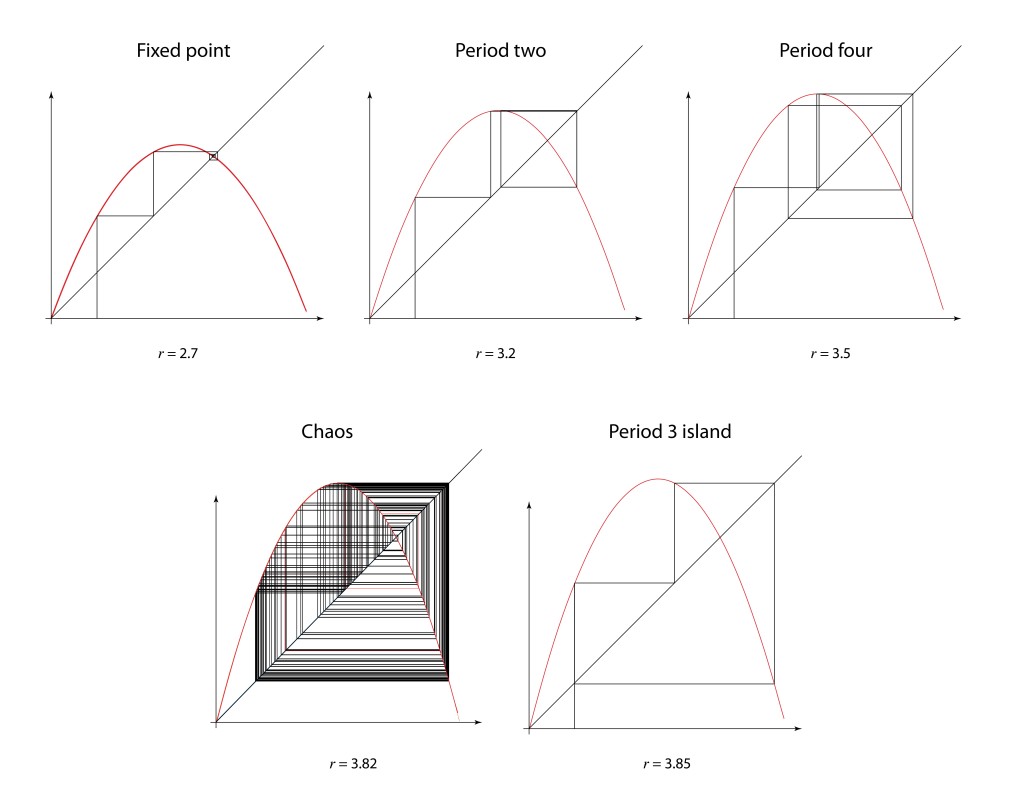
The onset of turbulence was an iconic problem in nonlinear physics with a long history and a long list of famous researchers studying it.  As far back as the Renaissance, Leonardo da Vinci had made detailed studies of water cascades, sketching whorls upon whorls in charcoal in his famous notebooks.  Heisenberg, oddly, wrote his PhD dissertation on the topic of turbulence even while he was inventing quantum mechanics on the side.  Kolmogorov in the 1940’s applied his probabilistic theories to turbulence, and this statistical approach dominated most studies up to the time when David Ruelle and Floris Takens published a paper in 1971 that took a nonlinear dynamics approach to the problem rather than statistical, identifying strange attractors in the nonlinear dynamical Navier-Stokes equations [10].  This paper coined the phrase “strange attractor”.  One of the distinct characteristics of their approach was the identification of a bifurcation cascade.  A single bifurcation means a sudden splitting of an orbit when a parameter is changed slightly.  In contrast, a bifurcation cascade was not just a single Hopf bifurcation, as seen in earlier nonlinear models, but was a succession of Hopf bifurcations that doubled the period each time, so that period-two attractors became period-four attractors, then period-eight and so on, coming fast and faster, until full chaos emerged.  A few years later Gollub and Swinney experimentally verified the cascade route to turbulence , publishing their results in 1975 [11]. 

Fig. 8 Bifurcation cascade of the logistic map.

Feigenbaum (1978)

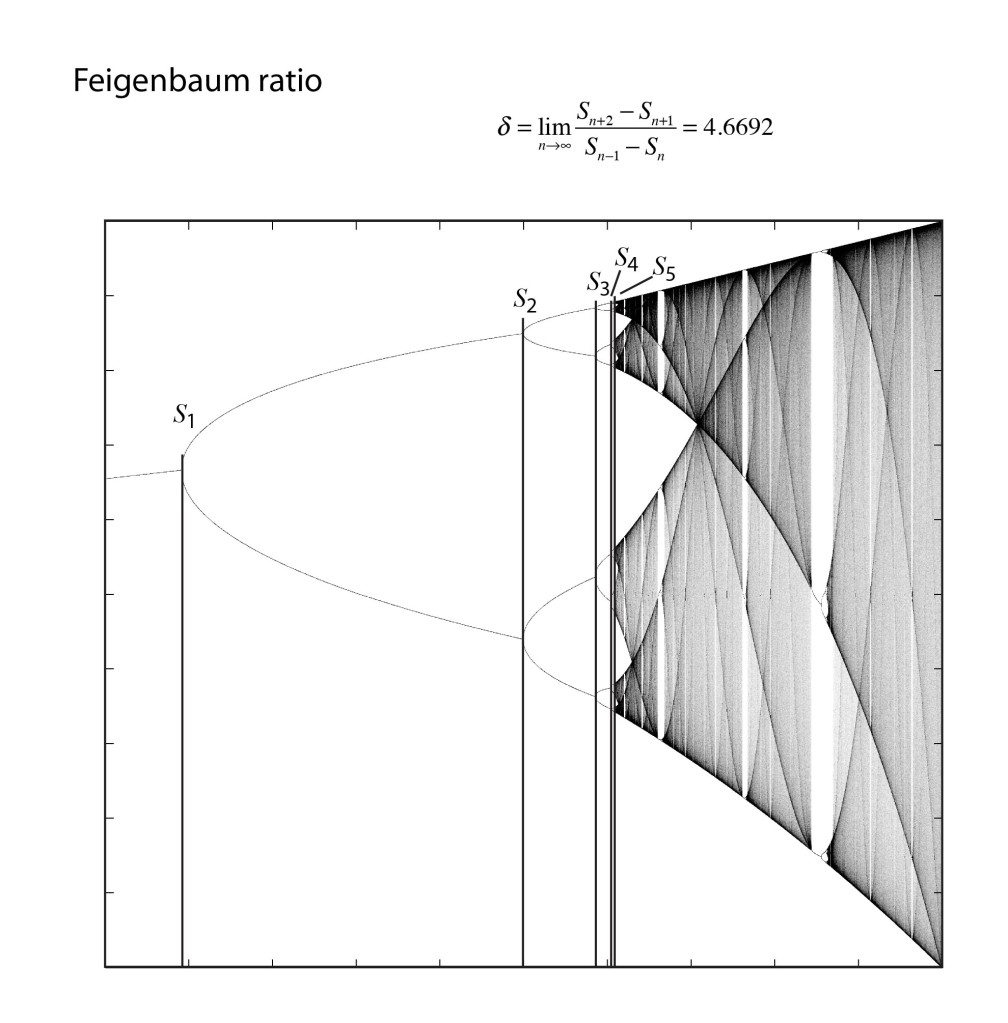
In 1976, computers were not common research tools, although hand-held calculators now were.  One of the most famous of this era was the Hewlett-Packard HP-65, and Feigenbaum pushed it to its limits.  He was particularly interested in the bifurcation cascade of the logistic map [12]—the way that bifurcations piled on top of bifurcations in a forking structure that showed increasing detail at increasingly fine scales.  Feigenbaum was, after all, a high-energy theorist and had overlapped at Cornell with Kenneth Wilson when he was completing his seminal work on the renormalization group approach to scaling phenomena.  Feigenbaum recognized a strong similarity between the bifurcation cascade and the ideas of real-space renormalization where smaller and smaller boxes were used to divide up space. 

One of the key steps in the renormalization procedure was the need to identify a ratio of the sizes of smaller structures to larger structures.  Feigenbaum began by studying how the bifurcations depended on the increasing growth rate.  He calculated the threshold values rm for each of the bifurcations, and then took the ratios of the intervals, comparing the previous interval (rm-1 – rm-2) to the next interval (rm – rm-1).  This procedure is like the well-known method to calculate the golden ratio = 1.61803 from the Fibonacci series, and Feigenbaum might have expected the golden ratio to emerge from his analysis of the logistic map.  After all, the golden ratio has a scary habit of showing up in physics, just like in the KAM theory.  However, as the bifurcation index m increased in Feigenbaum’s study, this ratio settled down to a limiting value of 4.66920.  Then he did what anyone would do with an unfamiliar number that emerges from a physical calculation—he tried to see if it was a combination of other fundamental numbers, like pi and Euler’s constant e, and even the golden ratio.  But none of these worked.  He had found a new number that had universal application to chaos theory [13]. 

Fig. 9 The ratio of the limits of successive cascades leads to a new universal number (the Feigenbaum number).

Gleick (1987)

By the mid-1980’s, chaos theory was seeping in to a broadening range of research topics that seemed to span the full breadth of science, from biology to astrophysics, from mechanics to chemistry. A particularly active group of chaos practitioners were J. Doyn Farmer, James Crutchfield, Norman Packard and Robert Shaw who founded the Dynamical Systems Collective at the University of California, Santa Cruz. One of the important outcomes of their work was a method to reconstruct the state space of a complex system using only its representative time series [14]. Their work helped proliferate the techniques of chaos theory into the mainstream. Many who started using these techniques were only vaguely aware of its long history until the science writer James Gleick wrote a best-selling history of the subject that brought chaos theory to the forefront of popular science [15]. And the rest, as they say, is history.

References

[1] Poincaré, H. and D. L. Goroff (1993). New methods of celestial mechanics. Edited and introduced by Daniel L. Goroff. New York, American Institute of Physics.

[2] J. Barrow-Green, Poincaré and the three body problem (London Mathematical Society, 1997).

[3] Cartwright,M.L.andJ.E.Littlewood(1945).“Onthenon-lineardifferential equation of the second order. I. The equation y′′ − k(1 – yˆ2)y′ + y = bλk cos(λt + a), k large.” Journal of the London Mathematical Society 20: 180–9. Discussed in Aubin, D. and A. D. Dalmedico (2002). “Writing the History of Dynamical Systems and Chaos: Longue DurÈe and Revolution, Disciplines and Cultures.” Historia Mathematica, 29: 273.

[4] Kolmogorov, A. N., (1954). “On conservation of conditionally periodic motions for a small change in Hamilton’s function.,” Dokl. Akad. Nauk SSSR (N.S.), 98: 527–30.

[5] Lorenz, E. N. (1963). “Deterministic Nonperiodic Flow.” Journal of the Atmo- spheric Sciences 20(2): 130–41.

[6] Arnold,V.I.(1997).“From superpositions to KAM theory,”VladimirIgorevich Arnold. Selected, 60: 727–40.

[7] Moser, J. (1962). “On Invariant Curves of Area-Preserving Mappings of an Annulus.,” Nachr. Akad. Wiss. Göttingen Math.-Phys, Kl. II, 1–20.

[8] Arnold, V. I. (1963). “Small denominators and problems of the stability of motion in classical and celestial mechanics (in Russian),” Usp. Mat. Nauk., 18: 91–192,; Arnold, V. I. (1964). “Instability of Dynamical Systems with Many Degrees of Freedom.” Doklady Akademii Nauk Sssr 156(1): 9.

[9] Chirikov, B. V. (1969). Research concerning the theory of nonlinear resonance and stochasticity. Institute of Nuclear Physics, Novosibirsk. 4. Note: The Standard Map Jn+1 =Jn +εsinθn θn+1 =θn +Jn+1
is plotted in Fig. 3.31 in Nolte, Introduction to Modern Dynamics (2015) on p. 139. For small perturbation ε, two fixed points appear along the line J = 0 corresponding to p/q = 1: one is an elliptical point (with surrounding small orbits) and the other is a hyperbolic point where chaotic behavior is first observed. With increasing perturbation, q elliptical points and q hyperbolic points emerge for orbits with winding numbers p/q with small denominators (1/2, 1/3, 2/3 etc.). Other orbits with larger q are warped by the increasing perturbation but are not chaotic. These orbits reside on invariant tori, known as the KAM tori, that do not disintegrate into chaos at small perturbation. The set of KAM tori is a Cantor-like set with non- zero measure, ensuring that stable behavior can survive in the presence of perturbations, such as perturbation of the Earth’s orbit around the Sun by Jupiter. However, with increasing perturbation, orbits with successively larger values of q disintegrate into chaos. The last orbits to survive in the Standard Map are the golden mean orbits with p/q = φ–1 and p/q = 2–φ. The critical value of the perturbation required for the golden mean orbits to disintegrate into chaos is surprisingly large at εc = 0.97.

[10] Ruelle,D. and F.Takens (1971).“OntheNatureofTurbulence.”Communications in Mathematical Physics 20(3): 167–92.

[11] Gollub, J. P. and H. L. Swinney (1975). “Onset of Turbulence in a Rotating Fluid.” Physical Review Letters, 35(14): 927–30.

[12] May, R. M. (1976). “Simple Mathematical-Models with very complicated Dynamics.” Nature, 261(5560): 459–67.

[13] M. J. Feigenbaum, “Quantitative Universality for a Class of Nnon-linear Transformations,” Journal of Statistical Physics 19, 25-52 (1978).

[14] Packard, N.; Crutchfield, J. P.; Farmer, J. Doyne; Shaw, R. S. (1980). “Geometry from a Time Series”. Physical Review Letters. 45 (9): 712–716.

[15] Gleick,J.(1987).Chaos:MakingaNewScience,NewYork:Viking.p.180.

by David D. Nolte

Life in a Solar System with a Super-sized Jupiter

There are many known super-Jupiters that orbit their stars—they are detected through a slight Doppler wobble they induce on their stars [1].  But what would become of a rocky planet also orbiting those stars as they feel the tug of both the star and the super planet?

This is not of immediate concern for us, because our solar system has had its current configuration of planets for over 4 billion years.  But there can be wandering interstellar planets or brown dwarfs that could visit our solar system, like Oumuamua did in 2017, but much bigger and able to scramble the planetary orbits. Such hypothesized astronomical objects have been given the name “Nemesis“, and it warrants thought on what living in an altered solar system might be like.

What would happen to Earth if Jupiter were 50 times bigger? Could we survive?

The Three-Body Problem

The Sun-Earth-Jupiter configuration is a three-body problem that has a long and interesting history, playing a key role in several aspects of modern dynamics [2].  There is no general analytical solution to the three-body problem.  To find the behavior of three mutually interacting bodies requires numerical solution.  However, there are subsets of the three-body problem that do yield to partial analytical approaches.  One of these is called the restricted three-body problem [3].  It consists of two massive bodies plus a third (nearly) massless body that all move in a plane.  This restricted problem was first tackled by Euler and later by Poincaré, who discovered the existence of chaos in its solutions.

The geometry of the restricted three-body problem is shown in Fig. 1. In this problem, take mass m1 = mS to be the Sun’s mass, m2 = mJ to be Jupiter’s mass, and the third (small) mass is the Earth. 

Fig. 1  The restricted 3-body problem in the plane.  The third mass is negligible relative to the first two masses that obey 2-body dynamics.

The equation of motion for the Earth is

where

and the parameter ξ characterizes the strength of the perturbation of the Earth’s orbit around the Sun.  The parameters for the Jupiter-Sun system are

with

for the 11.86 year journey of Jupiter around the Sun.  Eq. (1) is a four-dimensional non-autonomous flow

The solutions of an Earth orbit are shown in Fig.2.  The natural Earth-Sun-Jupiter system has a mass ratio mJ/mS = 0.001 for Jupiter relative to the Sun mass.  Even in this case, Jupiter causes perturbations of the Earth’s orbit by about one percent.  If the mass of Jupiter increases, the perturbations would grow larger until around ξ= 0.06 when the perturbations become severe and the orbit grows unstable.  The Earth gains energy from the momentum of the Sun-Jupiter system and can reach escape velocity.  The simulation for a mass ratio of 0.07 shows the Earth ejected from the Solar System.

Fig.2  Orbit of Earth as a function of the size of a Jupiter-like planet.  The natural system has a Jupiter-Earth mass ratio of 0.03.  As the size of Jupiter increases, the Earth orbit becomes unstable and can acquire escape velocity to escape from the Solar System. From body3.m. (Reprinted from Ref. [4])

The chances for ejection depends on initial conditions for these simulations, but generally the danger becomes severe when Jupiter is about 50 times larger than it currently is. Otherwise the Earth remains safe from ejection. However, if the Earth is to keep its climate intact, then Jupiter should not be any larger than about 5 times its current size. At the other extreme, for a planet 70 times larger than Jupiter, the Earth may not get ejected at once, but it can take a wild ride through the solar system. A simulation for a 70x Jupiter is shown in Fig. 3. In this case, the Earth is captured for a while as a “moon” of Jupiter in a very tight orbit around the super planet as it orbits the sun before it is set free again to orbit the sun in highly elliptical orbits. Because of the premise of the restricted three-body problem, the Earth has no effect on the orbit of Jupiter.

Fig. 3 Orbit of Earth for TJ = 11.86 years and ξ = 0.069. The radius of Jupiter is RJ = 5.2. Earth is “captured” for a while by Jupiter into a very tight orbit.

Resonance

If Nemesis were to swing by and scramble the solar system, then Jupiter might move closer to the Earth. More ominously, the period of Jupiter’s orbit could come into resonance with the Earth’s period. This occurs when the ratio of orbital periods is a ratio of small integers. Resonance can amplify small perturbations, so perhaps Jupiter would become a danger to Earth. However, the forces exerted by Jupiter on the Earth changes the Earth’s orbit and hence its period, preventing strict resonance to occur, and the Earth is not ejected from the solar system even for initial rational periods or larger planet mass. This is related to the famous KAM theory of resonances by Kolmogorov, Arnold and Moser that tends to protect the Earth from the chaos of the solar system. More often than not in these scenarios, the Earth is either captured by the super Jupiter, or it is thrown into a large orbit that is still bound to the sun. Some examples are given in the following figures.

Fig. 4 Orbit of Earth for an initial 8:1 resonance of TJ = 8 years and ξ = 0.073. The Radius of Jupiter is R = 4. Jupiter perturbs the Earth’s orbit so strongly that the 8:1 resonance is quickly removed.
Fig. 5 Earth orbit for TJ = 12 years and ξ = 0.071. The Earth is thrown into a nearly circular orbit beyond the orbit of Saturn.

Fig. 6 Earth Orbit for TJ = 4 years and ξ = 0.0615. Earth is thrown into an orbit of high ellipticity out to the orbit of Neptune.

Life on a planet in a solar system with two large bodies has been envisioned in dramatic detail in the science fiction novel “Three-Body Problem” by Liu Cixin about the Trisolarians of the closest known exoplanet to Earth–Proxima Centauri b.

By David D. Nolte, Feb. 28, 2022

Matlab Code: body3.m

function body3

clear

chsi0 = 1/1000;     % Earth-moon ratio = 1/317
wj0 = 2*pi/11.86;

wj = 2*pi/8;
chsi = 73*chsi0;    % (11.86,60) (11.86,67.5) (11.86,69) (11.86,70) (4,60) (4,61.5) (8,73) (12,71) 

rj = 5.203*(wj0/wj)^0.6666

rsun = chsi*rj/(1+chsi);
rjup = (1/chsi)*rj/(1+1/chsi);

r0 = 1-rsun;
y0 = [r0 0 0 2*pi/sqrt(r0)];

tspan = [0 300];
options = odeset('RelTol',1e-5,'AbsTol',1e-6);
[t,y] = ode45(@f5,tspan,y0,options);

figure(1)
plot(t,y(:,1),t,y(:,3))

figure(2)
plot(y(:,1),y(:,3),'k')
axis equal
axis([-6 6 -6 6])

RE = sqrt(y(:,1).^2 + y(:,3).^2);
stdRE = std(RE)

%print -dtiff -r800 threebody

    function yd = f5(t,y)
        
        xj = rjup*cos(wj*t);
        yj = rjup*sin(wj*t);
        xs = -rsun*cos(wj*t);
        ys = -rsun*sin(wj*t);
        rj32 = ((y(1) - xj).^2 + (y(3) - yj).^2).^1.5;
        r32 = ((y(1) - xs).^2 + (y(3) - ys).^2).^1.5;

        yp(1) = y(2);
        yp(2) = -4*pi^2*((y(1)-xs)/r32 + chsi*(y(1)-xj)/rj32);
        yp(3) = y(4);
        yp(4) = -4*pi^2*((y(3)-ys)/r32 + chsi*(y(3)-yj)/rj32);
 
        yd = [yp(1);yp(2);yp(3);yp(4)];

    end     % end f5

end

References:

[1] D. D. Nolte, “The Fall and Rise of the Doppler Effect,” Physics Today, vol. 73, no. 3, pp. 31-35, Mar (2020)

[2] J. Barrow-Green, Poincaré and the three body problem. London Mathematical Society, 1997.

[3] M. C. Gutzwiller, “Moon-Earth-Sun: The oldest three-body problem,” Reviews of Modern Physics, vol. 70, no. 2, pp. 589-639, Apr (1998)

[4] D. D. Nolte, Introduction to Modern Dynamics : Chaos, Networks, Space and Time, 1st ed. (Oxford University Press, 2015).

This Blog Post is a Companion to the undergraduate physics textbook Modern Dynamics: Chaos, Networks, Space and Time, 2nd ed. (Oxford, 2019) introducing Lagrangians and Hamiltonians, chaos theory, complex systems, synchronization, neural networks, econophysics and Special and General Relativity.

by David D. Nolte

Henri Poincaré and his Homoclinic Tangle

Will the next extinction-scale asteroid strike the Earth in our lifetime? 

This existential question—the question of our continued existence on this planet—is rhetorical, because there are far too many bodies in our solar system to accurately calculate all trajectories of all asteroids. 

The solar system is what is known as an N-body problem.  And even the N is not well determined.  The asteroid belt alone has over a million extinction-sized asteroids, and there are tens of millions of smaller ones that could still do major damage to life on Earth if they hit.  To have a hope of calculating even one asteroid trajectory do we ignore planetary masses that are too small?  What is too small?  What if we only consider the Sun, the Earth and Jupiter?  This is what Euler did in 1760, and he still had to make more assumptions.

Stability of the Solar System

Once Newton published his Principia, there was a pressing need to calculate the orbit of the Moon (see my blog post on the three-body problem).  This was important for navigation, because if the daily position of the moon could be known with sufficient accuracy, then ships would have a means to determine their longitude at sea.  However, the Moon, Earth and Sun are already a three-body problem, which still ignores the effects of Mars and Jupiter on the Moon’s orbit, not to mention the problem that the Earth is not a perfect sphere.  Therefore, to have any hope of success, toy systems that were stripped of all their obfuscating detail were needed.

Euler investigated simplified versions of the three-body problem around 1760, treating a body attracted to two fixed centers of gravity moving in the plane, and he solved it using elliptic integrals. When the two fixed centers are viewed in a coordinate frame that is rotating with the Sun-Earth system, it can come close to capturing many of the important details of the system. In 1762 Euler tried another approach, called the restricted three-body problem, where he considered a massless Moon attracted to a massive Earth orbiting a massive Sun, again all in the plane. Euler could not find general solutions to this problem, but he did stumble on an interesting special case when the three bodies remain collinear throughout their motions in a rotating reference frame.

It was not the danger of asteroids that was the main topic of interest in those days, but the question whether the Earth itself is in a stable orbit and is safe from being ejected from the Solar system.  Despite steadily improving methods for calculating astronomical trajectories through the nineteenth century, this question of stability remained open.

Poincaré and the King Oscar Prize of 1889

Some years ago I wrote an article for Physics Today called “The Tangled Tale of Phase Space” that tracks the historical development of phase space. One of the chief players in that story was Henri Poincaré (1854 – 1912). Henri Poincare was the Einstein before Einstein. He was a minor celebrity and was considered to be the greatest genius of his era. The event in his early career that helped launch him to stardom was a mathematics prize announced in 1887 to honor the birthday of King Oscar II of Sweden. The challenge problem was as simple as it was profound: Prove rigorously whether the solar system is stable.

This was the old N-body problem that had so far resisted solution, but there was a sense at that time that recent mathematical advances might make the proof possible. There was even a rumor that Dirichlet had outlined such a proof, but no trace of the outline could be found in his papers after his death in 1859.

The prize competition was announced in Acta Mathematica, written by the Swedish mathematician Gösta Mittag-Leffler. It stated:

Given a system of arbitrarily many mass points that attract each according to Newton’s law, under the assumption that no two points ever collide, try to find a representation of the coordinates of each point as a series in a variable that is some known function of time and for all of whose values the series converges uniformly.

The timing of the prize was perfect for Poincaré who was in his early thirties and just beginning to make his mark on mathematics. He was working on the theory of dynamical systems and was developing a new viewpoint that went beyond integrating single trajectories by focusing more broadly on whole classes of solutions. The question of the stability of the solar system seemed like a good problem to use to sharpen his mathematical tools. The general problem was still too difficult, so he began with Euler’s restricted three-body problem. He made steady progress, and along the way he invented an array of new techniques for studying the general properties of dynamical systems. One of these was the Poincaré section. Another was his set of integral invariants, one of which is recognized as the conservation of volume in phase space, also known as Liouville’s theorem, although it was Ludwig Boltzmann who first derived this result (see my Physics Today article). Eventually, he believed he had proven that the restricted three-body problem was stable.

By the time Poincaré had finished is prize submission, he had invented a new field of mathematical analysis, and the judges of the prize submission recognized it. Poincaré was named the winner, and his submission was prepared for publication in the Acta. However, Mittag-Leffler was a little concerned by a technical objection that had been raised, so he forwarded the comment to Poincaré for him to look at. At first, Poincaré thought the objection could easily be overcome, but as he worked on it and delved deeper, he had a sudden attack of panic. Trajectories near a saddle point did not converge. His proof of stability was wrong!

He alerted Mittag-Leffler to stop the presses, but it was too late. The first printing had been completed and review copies had already been sent to the judges. Mittag-Leffler immediately wrote to them asking for their return while Poincaré worked nonstop to produce a corrected copy. When he had completed his reanalysis, he had discovered a divergent feature of the solution to the dynamical problem near saddle points that is recognized today as the discovery of chaos. Poincaré paid for the reprinting of his paper out of his own pocket and (almost) all of the original printing was destroyed. This embarrassing moment in the life of a great mathematician was virtually forgotten until it was brought to light by the historian Barrow-Green in 1994 [1].

Poincaré is still a popular icon in France. Here is the Poincaré cafe in Paris.
A crater on the Moon is named after Poincaré.

Chaos in the Poincaré Return Map

Despite the fact that his conclusions on the stability of the 3-body problem flipped, Poincaré’s new tools for analyzing dynamical systems earned him the prize. He did not stop at his modified prize submission but continued working on systematizing his methods, publishing New Methods in Celestial Mechanics in several volumes through the 1890’s. It was here that he fully explored what happens when a trajectory approaches a saddle point of dynamical equilibrium.

The third volume of a three-book series that grew from Poincaré’s award-winning paper

To visualize a periodic trajectory, Poincaré invented a mathematical tool called a “first-return map”, also known as a Poincaré section. It was a way of taking a higher dimensional continuous trajectory and turning it into a simple iterated discrete map. Therefore, one did not need to solve continuous differential equations, it was enough to just iterate the map. In this way, complicated periodic, or nearly periodic, behavior could be explored numerically. However, even armed with this weapon, Poincaré found that iterated maps became unstable as a trajectory that originated from a saddle point approached another equivalent saddle point. Because the dynamics are periodic, the outgoing and incoming trajectories are opposite ends of the same trajectory, repeated with 2-pi periodicity. Therefore, the saddle point is also called a homoclinic point, meaning that trajectories in the discrete map intersect with themselves. (If two different trajectories in the map intersect, that is called a heteroclinic point.) When Poincaré calculated the iterations around the homoclinic point, he discovered a wild and complicated pattern in which a trajectory intersected itself many times. Poincaré wrote:

[I]f one seeks to visualize the pattern formed by these two curves and their infinite number of intersections … these intersections form a kind of lattice work, a weave, a chain-link network of infinitely fine mesh; each of the two curves can never cross itself, but it must fold back on itself in a very complicated way so as to recross all the chain-links an infinite number of times .… One will be struck by the complexity of this figure, which I am not even attempting to draw. Nothing can give us a better idea of the intricacy of the three-body problem, and of all the problems of dynamics in general…

Poincaré’s first view of chaos.

This was the discovery of chaos! Today we call this “lattice work” the “homoclinic tangle”. He could not draw it with the tools of his day … but we can!

Chirikov’s Standard Map

The restricted 3-body problem is a bit more complicated than is needed to illustrate Poincaré’s homoclinic tangle. A much simpler model is a discrete map called Chirikov’s Map or the Standard Map. It describes the Poincaré section of a periodically kicked oscillator that rotates or oscillates in the angular direction with an angular momentm J. The map has the simple form

in which the angular momentum in updated first, and then the angle variable is updated with the new angular momentum. When plotted on the (θ,J) plane, the standard map produces a beautiful kaleidograph of intertwined trajectories piercing the Poincaré plane, as shown in the figure below. The small points or dots are successive intersections of the higher-dimensional trajectory intersecting a plane. It is possible to trace successive points by starting very close to a saddle point (on the left) and connecting successive iterates with lines. These lines merge into the black trace in the figure that emerges along the unstable manifold of the saddle point on the left and approaches the saddle point on the right generally along the stable manifold.

Fig. Standard map for K = 0.97 at the transition to full chaos. The dark line is the trajectory of the unstable manifold emerging from the saddle point at (p,0). Note the wild oscillations as it approaches the saddle point at (3pi,0).

However, as the successive iterates approach the new saddle (which is really just the old saddle point because of periodicity) it crosses the stable manifold again and again, in ever wilder swings that diverge as it approaches the saddle point. This is just one trace. By calculating traces along all four stable and unstable manifolds and carrying them through to the saddle, a lattice work, or homoclinic tangle emerges.

Two of those traces originate from the stable manifolds, so to calculate their contributions to the homoclinic tangle, one must run these traces backwards in time using the inverse Chirikov map. This is

The four traces all intertwine at the saddle point in the figure below with a zoom in on the tangle in the next figure. This is the lattice work that Poincaré glimpsed in 1889 as he worked feverishly to correct the manuscript that won him the prize that established him as one of the preeminent mathematicians of Europe.

Fig. The homoclinic tangle caused by the folding of phase space trajectories as stable and unstable manifolds criss-cross in the Poincare map at the saddle point. This was the figure that Poincaré could not attempt to draw because of its complexity.
Fig. A zoom-in of the homoclinic tangle at the saddle point as the stable and unstable manifolds create a lattice of intersections. This is the fundamental origin of chaos and the sensitivity to initial conditions (SIC) that make forecasting almost impossible in chaotic systems.

The Physics of Life, the Universe and Everything:

Read more about the history of chaos theory in Galileo Unbound from Oxford University Press

Read Today.

Python Code: StandmapHom.py

(Python code on GitHub.)

#!/usr/bin/env python3
# -*- coding: utf-8 -*-
"""
StandmapHom.py
Created on Sun Aug  2  2020
"Introduction to Modern Dynamics" 2nd Edition (Oxford, 2019)
@author: nolte
"""

import numpy as np
from matplotlib import pyplot as plt
from numpy import linalg as LA

plt.close('all')

eps = 0.97

np.random.seed(2)

plt.figure(1)

for eloop in range(0,100):

    rlast = 2*np.pi*(0.5-np.random.random())
    thlast = 4*np.pi*np.random.random()
    
    rplot = np.zeros(shape=(200,))
    thetaplot = np.zeros(shape=(200,))
    for loop in range(0,200):
        rnew = rlast + eps*np.sin(thlast)
        thnew = np.mod(thlast+rnew,4*np.pi)
        
        thetaplot[loop] = np.mod(thnew-np.pi,4*np.pi)     
        rtemp = np.mod(rnew + np.pi,2*np.pi)
        rplot[loop] = rtemp - np.pi
  
        rlast = rnew
        thlast = thnew
        
    plt.plot(np.real(thetaplot),np.real(rplot),'o',ms=0.2)
    plt.xlim(xmin=np.pi,xmax=4*np.pi)
    plt.ylim(ymin=-2.5,ymax=2.5)
        
plt.savefig('StandMap')

K = eps
eps0 = 5e-7

J = [[1,1+K],[1,1]]
w, v = LA.eig(J)

My = w[0]
Vu = v[:,0]     # unstable manifold
Vs = v[:,1]     # stable manifold

# Plot the unstable manifold
Hr = np.zeros(shape=(100,150))
Ht = np.zeros(shape=(100,150))
for eloop in range(0,100):
    
    eps = eps0*eloop

    roldu1 = eps*Vu[0]
    thetoldu1 = eps*Vu[1]
    
    Nloop = np.ceil(-6*np.log(eps0)/np.log(eloop+2))
    flag = 1
    cnt = 0
    
    while flag==1 and cnt < Nloop:
        
        ru1 = roldu1 + K*np.sin(thetoldu1)
        thetau1 = thetoldu1 + ru1
        
        roldu1 = ru1
        thetoldu1 = thetau1
        
        if thetau1 > 4*np.pi:
            flag = 0
            
        Hr[eloop,cnt] = roldu1
        Ht[eloop,cnt] = thetoldu1 + 3*np.pi
        cnt = cnt+1
    
x = Ht[0:99,12] - 2*np.pi
x2 = 6*np.pi - x
y = Hr[0:99,12]
y2 = -y
plt.plot(x,y,linewidth =0.75)
plt.plot(x2,y2,linewidth =0.75)

del x,y
x = Ht[5:39,15] - 2*np.pi
x2 = 6*np.pi - x
y = Hr[5:39,15]
y2 = -y
plt.plot(x,y,linewidth =0.75)
plt.plot(x2,y2,linewidth =0.75)

del x,y
x = Ht[12:69,16] - 2*np.pi
x2 = 6*np.pi - x
y = Hr[12:69,16]
y2 = -y
plt.plot(x,y,linewidth =0.75)
plt.plot(x2,y2,linewidth =0.75)

del x,y
x = Ht[15:89,17] - 2*np.pi
x2 = 6*np.pi - x
y = Hr[15:89,17]
y2 = -y
plt.plot(x,y,linewidth =0.75)
plt.plot(x2,y2,linewidth =0.75)

del x,y
x = Ht[30:99,18] - 2*np.pi
x2 = 6*np.pi - x
y = Hr[30:99,18]
y2 = -y
plt.plot(x,y,linewidth =0.75)
plt.plot(x2,y2,linewidth =0.75)

# Plot the stable manifold
del Hr, Ht
Hr = np.zeros(shape=(100,150))
Ht = np.zeros(shape=(100,150))
#eps0 = 0.03
for eloop in range(0,100):
    
    eps = eps0*eloop

    roldu1 = eps*Vs[0]
    thetoldu1 = eps*Vs[1]
    
    Nloop = np.ceil(-6*np.log(eps0)/np.log(eloop+2))
    flag = 1
    cnt = 0
    
    while flag==1 and cnt < Nloop:
        
        thetau1 = thetoldu1 - roldu1
        ru1 = roldu1 - K*np.sin(thetau1)

        roldu1 = ru1
        thetoldu1 = thetau1
        
        if thetau1 > 4*np.pi:
            flag = 0
            
        Hr[eloop,cnt] = roldu1
        Ht[eloop,cnt] = thetoldu1
        cnt = cnt+1
    
x = Ht[0:79,12] + np.pi
x2 = 6*np.pi - x
y = Hr[0:79,12]
y2 = -y
plt.plot(x,y,linewidth =0.75)
plt.plot(x2,y2,linewidth =0.75)

del x,y
x = Ht[4:39,15] + np.pi
x2 = 6*np.pi - x
y = Hr[4:39,15]
y2 = -y
plt.plot(x,y,linewidth =0.75)
plt.plot(x2,y2,linewidth =0.75)

del x,y
x = Ht[12:69,16] + np.pi
x2 =  6*np.pi - x
y = Hr[12:69,16]
y2 = -y
plt.plot(x,y,linewidth =0.75)
plt.plot(x2,y2,linewidth =0.75)

del x,y
x = Ht[15:89,17] + np.pi
x2 =  6*np.pi - x
y = Hr[15:89,17]
y2 = -y
plt.plot(x,y,linewidth =0.75)
plt.plot(x2,y2,linewidth =0.75)

del x,y
x = Ht[30:99,18] + np.pi
x2 =  6*np.pi - x
y = Hr[30:99,18]
y2 = -y
plt.plot(x,y,linewidth =0.75)
plt.plot(x2,y2,linewidth =0.75)

References

[1] D. D. Nolte, “The tangled tale of phase space,” Physics Today, vol. 63, no. 4, pp. 33-38, Apr (2010)

[2] M. C. Gutzwiller, “Moon-Earth-Sun: The oldest three-body problem,” Reviews of Modern Physics, vol. 70, no. 2, pp. 589-639, Apr (1998)

[3] Barrow-Green J. Oscar II’s Prize Competition and the Error in Poindare’s Memoir on the Three Body Problem. Arch Hist Exact Sci 48: 107-131, 1994.

[4] Barrow-Green J. Poincaré and the three body problem. London Mathematical Society, 1997.

[5] https://the-moon.us/wiki/Poincar%C3%A9

[6] Poincaré H and Goroff DL. New methods of celestial mechanics … Edited and introduced by Daniel L. Goroff. New York: American Institute of Physics, 1993.