October 18, 2023December 4, 2023 by David D. Nolte

Relativistic Velocity Addition: Einstein’s Crucial Insight

The first step on the road to Einstein’s relativity was taken a hundred years earlier by an ironic rebel of physics—Augustin Fresnel. His radical (at the time) wave theory of light was so successful, especially the proof that it must be composed of transverse waves, that he was single-handedly responsible for creating the irksome luminiferous aether that would haunt physicists for the next century. It was only when Einstein combined the work of Fresnel with that of Hippolyte Fizeau that the aether was ultimately banished.

Augustin Fresnel: Ironic Rebel of Physics

Augustin Fresnel was an odd genius who struggled to find his place in the technical hierarchies of France. After graduating from the Ecole Polytechnique, Fresnel was assigned a mindless job overseeing the building of roads and bridges in the boondocks of France—work he hated. To keep himself from going mad, he toyed with physics in his spare time, and he stumbled on inconsistencies in Newton’s particulate theory of light that Laplace, a leader of the French scientific community, embraced as if it were revealed truth .

The final irony is that Einstein used Fresnel’s theoretical coefficient and Fizeau’s measurements—that had introduced aether drag in the first place—to show that there was no aether.

Fresnel rebelled, realizing that effects of diffraction could be explained if light were made of waves. He wrote up an initial outline of his new wave theory of light, but he could get no one to listen, until Francois Arago heard of it. Arago was having his own doubts about the particle theory of light based on his experiments on stellar aberration.

*Augustin Fresnel and Francois Arago (circa 1818*)

Stellar Aberration and the Fresnel Drag Coefficient

Stellar aberration had been explained by James Bradley in 1729 as the effect of the motion of the Earth relative to the motion of light “particles” coming from a star. The Earth’s motion made it look like the star was tilted at a very small angle (see my previous blog). That explanation had worked fine for nearly a hundred years, but then around 1810 Francois Arago at the Paris Observatory made extremely precise measurements of stellar aberration while placing finely ground glass prisms in front of his telescope. According to Snell’s law of refraction, which depended on the velocity of the light particles, the refraction angle should have been different at different times of the year when the Earth was moving one way or another relative to the speed of the light particles. But to high precision the effect was absent. Arago began to question the particle theory of light. When he heard about Fresnel’s work on the wave theory, he arranged a meeting, encouraging Fresnel to continue his work.

But at just this moment, in March of 1815, Napoleon returned from exile in Elba and began his march on Paris with a swelling army of soldiers who flocked to him. Fresnel rebelled again, joining a royalist militia to oppose Napoleon’s return. Napoleon won, but so did Fresnel, who was ironically placed under house arrest, which was like heaven to him. It freed him from building roads and bridges, giving him free time to do optics experiments in his mother’s house to support his growing theoretical work on the wave nature of light.

Arago convinced the authorities to allow Fresnel to come to Paris, where the two began experiments on diffraction and interference. By using polarizers to control the polarization of the interfering light paths, they concluded that light must be composed of transverse waves.

This brilliant insight was then followed by one of the great tragedies of science—waves needed a medium within which to propagate, so Fresnel conceived of the luminiferous aether to support it. Worse, the transverse properties of light required the aether to have a form of crystalline stiffness.

How could moving objects, like the Earth orbiting the sun, travel through such an aether without resistance? This was a serious problem for physics. One solution was that the aether was entrained by matter, so that as matter moved, the aether was dragged along with it. That solved the resistance problem, but it raised others, because it couldn’t explain Arago’s refraction measurements of aberration.

Fresnel realized that Arago’s null results could be explained if aether was only partially dragged along by matter. For instance, in the glass prisms used by Arago, the fraction of the aether being dragged along by the moving glass versus at rest would depend on the refractive index n of the glass. The speed of light in moving glass would then be

where c is the speed of light through stationary aether, v_g is the speed of the glass prism through the stationary aether, and V is the speed of light in the moving glass. The first term in the expression is the ordinary definition of the speed of light in stationary matter with the refractive index. The second term is called the Fresnel drag coefficient which he communicated to Arago in a letter in 1818. Even at the high speed of the Earth moving around the sun, this second term is a correction of only about one part in ten thousand. It explained Arago’s null results for stellar aberration, but it was not possible to measure it directly in the laboratory at that time.

Fizeau’s Moving Water Experiment

Hippolyte Fizeau has the distinction of being the first to measure the speed of light directly in an Earth-bound experiment. All previous measurements had been astronomical. The story of his ingenious use of a chopper wheel and long-distance reflecting mirrors placed across the city of Paris in 1849 can be found in Chapter 3 of Interference. However, two years later he completed an experiment that few at the time noticed but which had a much more profound impact on the history of physics.

In 1851, Fizeau modified an Arago interferometer to pass two interfering light beams along pipes of moving water. The goal of the experiment was to measure the aether drag coefficient directly and to test Fresnel’s theory of partial aether drag. The interferometer allowed Fizeau to measure the speed of light in moving water relative to the speed of light in stationary water. The results of the experiment confirmed Fresnel’s drag coefficient to high accuracy, which seemed to confirm the partial drag of aether by moving matter.

*Fizeau’s 1851 measurement of the speed of light in water using a modified Arago interferometer.* (Reprinted from Chapter 2: Interference.)

This result stood for thirty years, presenting its own challenges for physicist exploring theories of the aether. The sophistication of interferometry improved over that time, and in 1881 Albert Michelson used his newly-invented interferometer to measure the speed of the Earth through the aether. He performed the experiment in the Potsdam Observatory outside Berlin, Germany, and found the opposite result of complete aether drag, contradicting Fizeau’s experiment. Later, after he began collaborating with Edwin Morley at Case and Western Reserve Colleges in Cleveland, Ohio, the two repeated Fizeau’s experiment to even better precision, finding once again Fresnel’s drag coefficient, followed by their own experiment, known now as “the Michelson-Morley Experiment” in 1887, that found no effect of the Earth’s movement through the aether.

The two experiments—Fizeau’s measurement of the Fresnel drag coefficient, and Michelson’s null measurement of the Earth’s motion—were in direct contradiction with each other. Based on the theory of the aether, they could not both be true.

But where to go from there? For the next 15 years, there were numerous attempts to put bandages on the aether theory, from Fitzgerald’s contraction to Lorenz’ transformations, but it all seemed like kludges built on top of kludges. None of it was elegant—until Einstein had his crucial insight.

Einstein’s Insight

While all the other top physicists at the time were trying to save the aether, taking its real existence as a fact of Nature to be reconciled with experiment, Einstein took the opposite approach—he assumed that the aether did not exist and began looking for what the experimental consequences would be.

From the days of Galileo, it was known that measured speeds depended on the frame of reference. This is why a knife dropped by a sailor climbing the mast of a moving ship strikes at the base of the mast, falling in a straight line in the sailor’s frame of reference, but an observer on the shore sees the knife making an arc—velocities of relative motion must add. But physicists had over-generalized this result and tried to apply it to light—Arago, Fresnel, Fizeau, Michelson, Lorenz—they were all locked in a mindset.

Einstein stepped outside that mindset and asked what would happen if all relatively moving observers measured the same value for the speed of light, regardless of their relative motion. It was just a little algebra to find that the way to add the speed of light c to the speed of a moving reference frame v_ref was

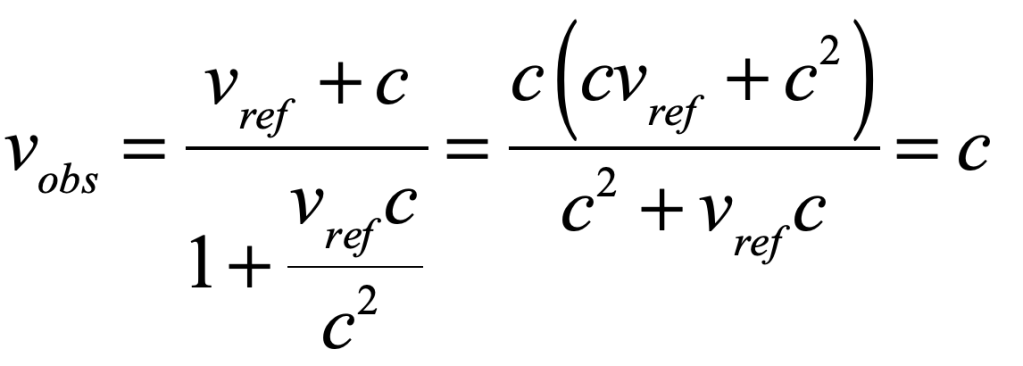
where the numerator was the usual Galilean relativity velocity addition, and the denominator was required to enforce the constancy of observed light speeds. Therefore, adding the speed of light to the speed of a moving reference frame gives back simply the speed of light.

Generalizing this equation for general velocity addition between moving frames gives

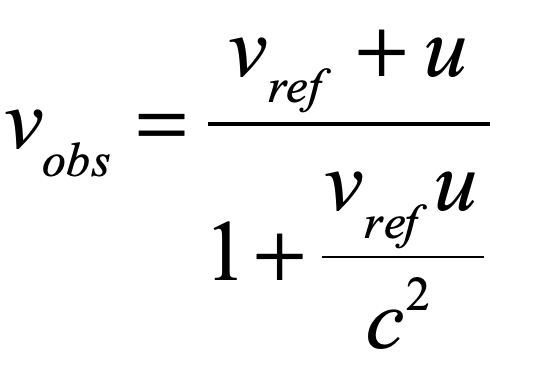
where u is now the speed of some moving object being added the the speed of a reference frame, and v_obs is the “net” speed observed by some “external” observer . This is Einstein’s famous equation for relativistic velocity addition (see pg. 12 of the English translation). It ensures that all observers with differently moving frames all measure the same speed of light, while also predicting that no velocities for objects can ever exceed the speed of light.

This last fact is a consequence, not an assumption, as can be seen by letting the reference speed v_ref increase towards the speed of light so that v_ref ≈ c, then

so that the speed of an object launched in the forward direction from a reference frame moving near the speed of light is still observed to be no faster than the speed of light

All of this, so far, is theoretical. Einstein then looked to find some experimental verification of his new theory of relativistic velocity addition, and he thought of the Fizeau experimental measurement of the speed of light in moving water. Applying his new velocity addition formula to the Fizeau experiment, he set v_ref = v_water and u = c/n and found

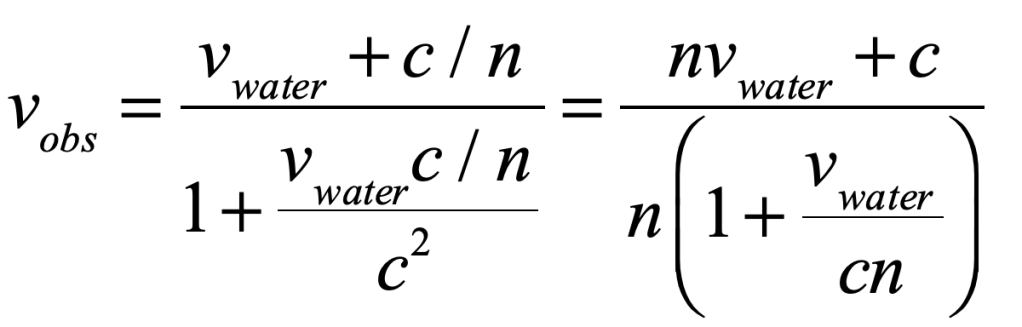
The second term in the denominator is much smaller that unity and is expanded in a Taylor’s expansion

The last line is exactly the Fresnel drag coefficient!

Therefore, Fizeau, half a century before, in 1851, had already provided experimental verification of Einstein’s new theory for relativistic velocity addition! It wasn’t aether drag at all—it was relativistic velocity addition.

From this point onward, Einstein followed consequence after inexorable consequence, constructing what is now called his theory of Special Relativity, complete with relativistic transformations of time and space and energy and matter—all following from a simple postulate of the constancy of the speed of light and the prescription for the addition of velocities.

The final irony is that Einstein used Fresnel’s theoretical coefficient and Fizeau’s measurements, that had established aether drag in the first place, as the proof he needed to show that there was no aether. It was all just how you looked at it.

The Anharmonic Harmonic Oscillator

Harmonic oscillators are one of the fundamental elements of physical theory. They arise so often in so many different contexts that they can be viewed as a central paradigm that spans all aspects of physics. Some famous physicists have been quoted to say that the entire universe is composed of simple harmonic oscillators (SHO).

Despite the physicist’s love affair with it, the SHO is pathological! First, it has infinite frequency degeneracy which makes it prone to the slightest perturbation that can tip it into chaos, in contrast to non-harmonic cyclic dynamics that actually protects us from the chaos of the cosmos (see my Blog on Chaos in the Solar System). Second, the SHO is nowhere to be found in the classical world. Linear oscillators are purely harmonic, with a frequency that is independent of amplitude—but no such thing exists! All oscillators must be limited, or they could take on infinite amplitude and infinite speed, which is nonsense. Even the simplest of simple harmonic oscillators would be limited by nothing other than the speed of light. Relativistic effects would modify the linearity, especially through time dilation effects, rendering the harmonic oscillator anharmonic.

Despite the physicist’s love affair with it, the SHO is pathological!

Therefore, for students of physics as well as practitioners, it is important to break the shackles imposed by the SHO and embrace the anharmonic harmonic oscillator as the foundation of physics. Here is a brief survey of several famous anharmonic oscillators in the history of physics, followed by the mathematical analysis of the relativistic anharmonic linear-spring oscillator.

Anharmonic Oscillators

Anharmonic oscillators have a long venerable history with many varieties. Many of these have become central models in systems as varied as neural networks, synchronization, grandfather clocks, mechanical vibrations, business cycles, ecosystem populations and more.

Christiaan Huygens

Already by the mid 1600’s Christiaan Huygens (1629 – 1695) knew that the pendulum becomes slower when it has larger amplitudes. The pendulum was one of the best candidates for constructing an accurate clock needed for astronomical observations and for the determination of longitude at sea. Galileo (1564 – 1642) had devised the plans for a rudimentary pendulum clock that his son attempted to construct, but the first practical pendulum clock was invented and patented by Huygens in 1657. However, Huygens’ modified verge escapement required his pendulum to swing with large amplitudes, which brought it into the regime of anharmonicity. The equations of the simple pendulum are truly simple, but the presence of the sinθ makes it the simplest anharmonic oscillator.

Therefore, Huygens searched for the mathematical form of a tautochrone curve for the pendulum (a curve that is traversed with equal times independently of amplitude) and in the process he invented the involutes and evolutes of a curve—precursors of the calculus. The answer to the tautochrone question is a cycloid (see my Blog on Huygen’s Tautochrone Curve).

Hermann von Helmholtz

Hermann von Helmholtz (1821 – 1894) was possibly the greatest German physicist of his generation—an Einstein before Einstein—although he began as a medical doctor. His study of muscle metabolism, drawing on the early thermodynamic work of Carnot, Clapeyron and Joule, led him to explore and to express the conservation of energy in its clearest form. Because he postulated that all forms of physical processes—electricity, magnetism, heat, light and mechanics—contributed to the interconversion of energy, he sought to explore them all, bringing his research into the mainstream of physics. His laboratory in Berlin became world famous, attracting to his laboratory the early American physicists Henry Rowland (founder and first president of the American Physical Society) and Albert Michelson (first American Nobel prize winner).

Even the simplest of simple harmonic oscillators would be limited by nothing other than the speed of light.

Helmholtz also pursued a deep interest in the physics of sensory perception such as sound. This research led to his invention of the Helmholtz oscillator which is a highly anharmonic relaxation oscillator in which a tuning fork was placed near an electromagnet that was powered by a mercury switch attached to the fork. As the tuning fork vibrated, the mercury came in and out of contact with it, turning on and off the magnet, which fed back on the tuning fork, and so on, enabling the device, once started, to continue oscillating without interruption. This device is called a tuning-fork resonator, and it became the first door-bell buzzers. (These are not to be confused with Helmholtz resonances that are formed when blowing across the open neck of a beer bottle.)

Lord Rayleigh

Baron John Strutt, the Lord Rayleigh (1842 – 1919) like Helmholtz also was a generalist and had a strong interest in the physics of sound. He was inspired by Helmholtz’ oscillator to consider general nonlinear anharmonic oscillators mathematically. He was led to consider the effects of anharmonic terms added to the harmonic oscillator equation. in a paper published in the Philosophical Magazine issue of 1883 with the title On Maintained Vibrations, he introduced an equation to describe the self-oscillation by adding an extra term to a simple harmonic oscillator. The extra term depended on the cube of the velocity, representing a balance between the gain of energy from a steady force and natural dissipation by friction. Rayleigh suggested that this equation applied to a wide range of self-oscillating systems, such as violin strings, clarinet reeds, finger glasses, flutes, organ pipes, among others (see my Blog on Rayleigh’s Harp.)

Georg Duffing

The first systematic study of quadratic and cubic deviations from the harmonic potential was performed by the German engineer George Duffing (1861 – 1944) under the conditions of a harmonic drive. The Duffing equation incorporates inertia, damping, the linear spring and nonlinear deviations.

Fig. 1 The Duffing equation adds a nonlinear term to the spring force when alpha is positive, stiffening or weakening it for larger excursions when beta is positive or negative, respectively. And by making alpha negative and beta positive, it describes a damped driven double-well potential.

Duffing confirmed his theoretical predictions with careful experiments and established the lowest-order corrections to ideal masses on springs. His work was rediscovered in the 1960’s after Lorenz helped launch numerical chaos studies. Duffing’s driven potential becomes especially interesting when α is negative and β is positive, creating a double-well potential. The driven double-well is a classic chaotic system (see my blog on Duffing’s Oscillator).

Balthasar van der Pol

Autonomous oscillators are one of the building blocks of complex systems, providing the fundamental elements for biological oscillators, neural networks, business cycles, population dynamics, viral epidemics, and even the rings of Saturn. The most famous autonomous oscillator (after the pendulum clock) is named for a Dutch physicist, Balthasar van der Pol (1889 – 1959), who discovered the laws that govern how electrons oscillate in vacuum tubes, but the dynamical system that he developed has expanded to become the new paradigm of cyclic dynamical systems to replace the SHO (see my Blog on GrandFather Clocks.)

Fig. 2 The van der Pol equation is the standard simple harmonic oscillator with a gain term that saturates for large excursions leading to a limit cycle oscillator.

Turning from this general survey, let’s find out what happens when special relativity is added to the simplest SHO [1].

Relativistic Linear-Spring Oscillator

The theory of the relativistic one-dimensional linear-spring oscillator starts from a relativistic Lagrangian of a free particle (with no potential) yielding the generalized relativistic momentum

The Lagrangian that accomplishes this is [2]

where the invariant 4-velocity is

When the particle is in a potential, the Lagrangian becomes

The action integral that is minimized is

and the Lagrangian for integration of the action integral over proper time is

The relativistic modification in the potential energy term of the Lagrangian is not in the spring constant, but rather is purely a time dilation effect. This is captured by the relativistic Lagrangian

where the dot is with respect to proper time τ. The classical potential energy term in the Lagrangian is multiplied by the relativistic factor γ, which is position dependent because of the non-constant speed of the oscillator mass. The Euler-Lagrange equations are

where the subscripts in the variables are a = 0, 1 for the time and space dimensions, respectively. The derivative of the time component of the 4-vector is

From the derivative of the Lagrangian with respect to speed, the following result is derived

where E is the constant total relativistic energy. Therefore,

which provides an expression for the derivative of the coordinate time with respect to the proper time where

The position-dependent γ(x) factor is then

The Euler-Lagrange equation with a = 1 is

which gives

providing the flow equations for the (an)harmonic oscillator with respect to proper time

This flow represents a harmonic oscillator modified by the γ(x) factor, due to time dilation, multiplying the spring force term. Therefore, at relativistic speeds, the oscillator is no longer harmonic even though the spring constant remains truly a constant. The term in parentheses effectively softens the spring for larger displacement, and hence the frequency of oscillation becomes smaller.

The state-space diagram of the anharmonic oscillator is shown in Fig. 3 with respect to proper time (the time read on a clock co-moving with the oscillator mass). At low energy, the oscillator is harmonic with a natural period of the SHO. As the maximum speed exceeds β = 0.8, the period becomes longer and the trajectory less sinusoidal. The position and speed for β = 0.9999 is shown in Fig. 4. The mass travels near the speed of light as it passes the origin, producing significant time dilation at that instant. The average time dilation through a single cycle is about a factor of three, despite the large instantaneous γ = 70 when the mass passes the origin.

Fig. 3 State-space diagram in relativistic units relative to proper time of a relativistic (an)harmonic oscillator with a constant spring constant for several relative speeds β. The anharmonicity becomes pronounced above β = 0.8.

Fig. 4 Position and speed in relativistic units relative to proper time of a relativistic (an)harmonic oscillator with a constant spring constant for β = 0.9999. The period of oscillation in this simulation is nearly three times longer than the natural frequency at small amplitudes.

By David D. Nolte, May 29, 2022

[1] W. Moreau, R. Easther, and R. Neutze, “RELATIVISTIC (AN)HARMONIC OSCILLATOR,” American Journal of Physics, Article vol. 62, no. 6, pp. 531-535, Jun (1994)

[2] D. D. Nolte, Introduction to Modern Dynamics: Chaos, Networks, Space and Time, 2nd. ed. (Oxford University Press, 2019)

This Blog Post is a Companion to the undergraduate physics textbook Modern Dynamics: Chaos, Networks, Space and Time, 2nd ed. (Oxford, 2019) introducing Lagrangians and Hamiltonians, chaos theory, complex systems, synchronization, neural networks, econophysics and Special and General Relativity.

March 23, 2022June 1, 2023 by David D. Nolte

The Physics of Starflight: Proxima Centauri b or Bust!

The ability to travel to the stars has been one of mankind’s deepest desires. Ever since we learned that we are just one world in a vast universe of limitless worlds, we have yearned to visit some of those others. Yet nature has thrown up an almost insurmountable barrier to that desire–the speed of light. Only by traveling at or near the speed of light may we venture to far-off worlds, and even then, decades or centuries will pass during the voyage. The vast distances of space keep all the worlds isolated–possibly for the better.

Yet the closest worlds are not so far away that they will always remain out of reach. The very limit of the speed of light provides ways of getting there within human lifetimes. The non-intuitive effects of special relativity come to our rescue, and we may yet travel to the closest exoplanet we know of.

Proxima Centauri b

The closest habitable Earth-like exoplanet is Proxima Centauri b, orbiting the red dwarf star Proxima Centauri that is about 4.2 lightyears away from Earth. The planet has a short orbital period of only about 11 Earth days, but the dimness of the red dwarf puts the planet in what may be a habitable zone where water is in liquid form. Its official discovery date was August 24, 2016 by the European Southern Observatory in the Atacama Desert of Chile using the Doppler method. The Alpha Centauri system is a three-star system, and even before the discovery of the planet, this nearest star system to Earth was the inspiration for the Hugo-Award winning sci-fi trilogy The Three Body Problem by Chinese author Liu Cixin, originally published in 2008.

It may seem like a coincidence that the closest Earth-like planet to Earth is in the closest star system to Earth, but it says something about how common such exoplanets may be in our galaxy.

Artist’s rendition of Proxima Centauri b. From WikiCommons.

Breakthrough Starshot

There are already plans to send centimeter-sized spacecraft to Alpha Centauri. One such project that has received a lot of press is Breakthrough Starshot, a project of the Breakthrough Initiatives. Breakthrough Starshot would send around 1000 centimeter-sized camera-carrying laser-fitted spacecraft with 5-meter-diameter solar sails propelled by a large array of high-power lasers. The reason there are so many of these tine spacecraft is because of the collisions that are expected to take place with interstellar dust during the voyage. It is possible that only a few dozen of the craft will finally make it to Alpha Centauri intact.

Relative locations of the stars of the Alpha Centauri system. From ScienceNews.

As these spacecraft fly by the Alpha Centauri system, possibly within one hundred million miles of Proxima Centauri b, their tiny HR digital cameras will take pictures of the planet’s surface with enough resolution to see surface features. The on-board lasers will then transmit the pictures back to Earth. The travel time to the planet is expected to be 20 or 30 years, plus the four years for the laser information to make it back to Earth. Therefore, it would take a quarter century after launch to find out if Proxima Centauri b is habitable or not. The biggest question is whether it has an atmosphere. The red dwarf it orbits sends out catastrophic electromagnetic bursts that could strip the planet of its atmosphere thus preventing any chance for life to evolve or even to be sustained there if introduced.

There are multiple projects under consideration for travel to the Alpha Centauri systems. Even NASA has a tentative mission plan called the 2069 Mission (100 year anniversary of the Moon landing). This would entail a single spacecraft with a much larger solar sail than the small starshot units. Some of the mission plans proposed star-drive technology, such as nuclear propulsion systems, rather than light sails. Some of these designs could sustain a 1-g acceleration throughout the entire mission. It is intriguing to do the math on what such a mission could look like, in terms of travel time. Could we get an unmanned probe to Alpha Centauri in a matter of years? Let’s find out.

Special Relativity of Acceleration

The most surprising aspect of deriving the properties of relativistic acceleration using special relativity is that it works at all. We were all taught as young physicists that special relativity deals with inertial frames in constant motion. So the idea of frames that are accelerating might first seem to be outside the scope of special relativity. But one of Einstein’s key insights, as he sought to extend special relativity towards a more general theory, was that one can define a series of instantaneously inertial co-moving frames relative to an accelerating body. In other words, at any instant in time, the accelerating frame has an inertial co-moving frame. Once this is defined, one can construct invariants, just as in usual special relativity. And these invariants unlock the full mathematical structure of accelerating objects within the scope of special relativity.

For instance, the four-velocity and the four-acceleration in a co-moving frame for an object accelerating at g are given by

The object is momentarily stationary in the co-moving frame, which is why the four-velocity has only the zeroth component, and the four-acceleration has simply g for its first component.

Armed with these four-vectors, one constructs the invariants

and

This last equation is solved for the specific co-moving frame as

But the invariant is more general, allowing the expression

which yields

From these, putting them all together, one obtains the general differential equations for the change in velocity as a set of coupled equations

The solution to these equations is

where the unprimed frame is the lab frame (or Earth frame), and the primed frame is the frame of the accelerating object, for instance a starship heading towards Alpha Centauri. These equations allow one to calculate distances, times and speeds as seen in the Earth frame as well as the distances, times and speeds as seen in the starship frame. If the starship is accelerating at some acceleration g’ other than g, then the results are obtained simply by replacing g by g’ in the equations.

Relativistic Flight

It turns out that the acceleration due to gravity on our home planet provides a very convenient (but purely coincidental) correspondence

With a similarly convenient expression

These considerably simplify the math for a starship accelerating at g.

Let’s now consider a starship accelerating by g for the first half of the flight to Alpha Centauri, turning around and decelerating at g for the second half of the flight, so that the starship comes to a stop at its destination. The equations for the times to the half-way point are

This means at the midpoint that 1.83 years have elapsed on the starship, and about 3 years have elapsed on Earth. The total time to get to Alpha Centauri (and come to a stop) is then simply

It is interesting to look at the speed at the midpoint. This is obtained by

which is solved to give

This amazing result shows that the starship is traveling at 95% of the speed of light at the midpoint when accelerating at the modest value of g for about 3 years. Of course, the engineering challenges for providing such an acceleration for such a long time are currently prohibitive … but who knows? There is a lot of time ahead of us for technology to advance to such a point in the next century or so.

Figure. Time lapsed inside the spacecraft and on Earth for the probe to reach Alpha Centauri as a function of the acceleration of the craft. At 10 g’s, the time elapsed on Earth is a little less than 5 years. However, the signal sent back will take an additional 4.37 years to arrive for a total time of about 9 years.

Matlab alphacentaur.m

% alphacentaur.m
clear
format compact

g0 = 1;
L = 4.37;

for loop = 1:100
    
    g = 0.1*loop*g0;
    
    taup = (1/g)*acosh(g*L/2 + 1);
    tearth = (1/g)*sinh(g*taup);
    
    tauspacecraft(loop) = 2*taup;
    tlab(loop) = 2*tearth;
    
    acc(loop) = g;
    
end

figure(1)
loglog(acc,tauspacecraft,acc,tlab,'LineWidth',2)
legend('Space Craft','Earth Frame','FontSize',18)
xlabel('Acceleration (g)','FontSize',18)
ylabel('Time (years)','FontSize',18)
dum = set(gcf,'Color','White');
H = gca;
H.LineWidth = 2;
H.FontSize = 18;

To Centauri and Beyond

Once we get unmanned probes to Alpha Centauri, it opens the door to star systems beyond. The next closest are Barnards star at 6 Ly away, Luhman 16 at 6.5 Ly, Wise at 7.4 Ly, and Wolf 359 at 7.9 Ly. Several of these are known to have orbiting exoplanets. Ross 128 at 11 Ly and Lyuten at 12.2 Ly have known earth-like planets. There are about 40 known earth-like planets within 40 lightyears from Earth, and likely there are more we haven’t found yet. It is almost inconceivable that none of these would have some kind of life. Finding life beyond our solar system would be a monumental milestone in the history of science. Perhaps that day will come within this century.

By David D. Nolte, March 23, 2022

The Transverse Doppler Effect and Relativistic Time Dilation

One of the hardest aspects to grasp about relativity theory is the question of whether an event “looks as if” it is doing something, or whether it “actually is” doing something.

Take, for instance, the classic twin paradox of relativity theory in which there are twins who wear identical high-precision wrist watches. One of them rockets off to Alpha Centauri at relativistic speeds and returns while the other twin stays on Earth. Each twin sees the other twin’s clock running slowly because of relativistic time dilation. Yet when they get back together and, standing side-by-side, they compare their watches—the twin who went to Alpha Centauri is actually younger than the other, despite the paradox. The relativistic effect of time dilation is “real”, not just apparent, regardless of whether they come back together to do the comparison.

Yet this understanding of relativistic effects took many years, even decades, to gain acceptance after Einstein proposed them. He was aware himself that key experiments were required to prove that relativistic effects are real and not just apparent.

Einstein and the Transverse Doppler Effect

In 1905 Einstein used his new theory of special relativity to predict observable consequences that included relativistic velocity addition and a general treatment of the relativistic Doppler effect [1]. This included the effects of time dilation in addition to the longitudinal effect of the source chasing the wave. Time dilation produced a correction to Doppler’s original expression for the longitudinal effect that became significant at speeds approaching the speed of light. More significantly, it predicted a transverse Doppler effect for a source moving along a line perpendicular to the line of sight to an observer. This effect had not been predicted either by Christian Doppler (1803 – 1853) or by Woldemar Voigt (1850 – 1919).

( Read article in Physics Today on the history of the Doppler effect [2] )

Despite the generally positive reception of Einstein’s theory of special relativity, some of its consequences were anathema to many physicists at the time. A key stumbling block was the question whether relativistic effects, like moving clocks running slowly, were only apparent, or were actually real, and Einstein had to fight to convince others of its reality. When Johannes Stark (1874 – 1957) observed Doppler line shifts in ion beams called “canal rays” in 1906 (Stark received the 1919 Nobel prize in part for this discovery) [3], Einstein promptly published a paper suggesting how the canal rays could be used in a transverse geometry to directly detect time dilation through the transverse Doppler effect [4]. Thirty years passed before the experiment was performed with sufficient accuracy by Herbert Ives and G. R. Stilwell in 1938 to measure the transverse Doppler effect [5]. Ironically, even at this late date, Ives and Stilwell were convinced that their experiment had disproved Einstein’s time dilation by supporting Lorentz’ contraction theory of the electron. The Ives-Stilwell experiment was the first direct test of time dilation, followed in 1940 by muon lifetime measurements [6].

A) Transverse Doppler Shift Relative to Emission Angle

The Doppler effect varies between blue shifts in the forward direction to red shifts in the backward direction, with a smooth variation in Doppler shift as a function of the emission angle. Consider the configuration shown in Fig. 1 for light emitted from a source moving at speed v and emitting at an angle θ₀ in the receiver frame. The source moves a distance vT in the time of a single emission cycle (assume a harmonic wave). In that time T (which is the period of oscillation of the light source — or the period of a clock if we think of it putting out light pulses) the light travels a distance cT before another cycle begins (or another pulse is emitted).

Fig. 1 Configuration for detection of Doppler shifts for emission angle θ₀. The light source travels a distance vT during the time of a single cycle, while the wavefront travels a distance cT towards the detector.

[ See YouTube video on the derivation of the transverse Doppler Effect.]

The observed wavelength in the receiver frame is thus given by

where T is the emission period of the moving source. Importantly, the emission period is time dilated relative to the proper emission time of the source

Therefore,

This expression can be evaluated for several special cases:

a) θ₀ = 0 for forward emission

which is the relativistic blue shift for longitudinal motion in the direction of the receiver.

b) θ₀ = π for backward emission

which is the relativistic red shift for longitudinal motion away from the receiver

c) θ₀ = π/2 for transverse emission

This transverse Doppler effect for emission at right angles is a red shift, caused only by the time dilation of the moving light source. This is the effect proposed by Einstein and observed by Stark that proved moving clocks tick slowly. But it is not the only way to view the transverse Doppler effect.

B) Transverse Doppler Shift Relative to Angle at Reception

A different option for viewing the transverse Doppler effect is the angle to the moving source at the moment that the light is detected. The geometry of this configuration relative to the previous is illustrated in Fig. 2.

Fig. 2 The detection point is drawn at a finite distance. However, the relationship between θ₀ and θ₁ is independent of the distance to the detector

The transverse distance to the detection point is

The length of the line connecting the detection point P with the location of the light source at the moment of detection is (using the law of cosines)

Combining with the first equation gives

An equivalent expression is obtained as

Note that this result, relating θ₁ to θ₀, is independent of the distance to the observation point.

When θ₁ = π/2, then

yielding

for which the Doppler effect is

which is a blue shift. This creates the unexpected result that sin θ₀ = π/2 produces a red shift, while sin θ₁ = π/2 produces a blue shift. The question could be asked: which one represents time dilation? In fact, it is sin θ₀ = π/2 that produces time dilation exclusively, because in that configuration there is no foreshortening effect on the wavelength–only the emission time.

C) Compromise: The Null Transverse Doppler Shift

The previous two configurations each could be used as a definition for the transverse Doppler effect. But one gives a red shift and one gives a blue shift, which seems contradictory. Therefore, one might try to strike a compromise between these two cases so that sin θ₁ = sin θ₀, and the configuration is shown in Fig. 3.

This is the case when θ₁ + θ₂ = π. The sines of the two angles are equal, yielding

and

which is solved for

Inserting this into the Doppler equation gives

where the Taylor’s expansion of the denominator (at low speed) cancels the numerator to give zero net Doppler shift. This compromise configuration represents the condition of null Doppler frequency shift. However, for speeds approaching the speed of light, the net effect is a lengthening of the wavelength, dominated by time dilation, causing a red shift.

D) Source in Circular Motion Around Receiver

An interesting twist can be added to the problem of the transverse Doppler effect: put the source or receiver into circular motion, one about the other. In the case of a source in circular motion around the receiver, it is easy to see that this looks just like case A) above for θ₀ = π/2, which is the red shift caused by the time dilation of the moving source

However, there is the possible complication that the source is no longer in an inertial frame (it experiences angular acceleration) and therefore it is in the realm of general relativity instead of special relativity. In fact, it was Einstein’s solution to this problem that led him to propose the Equivalence Principle and make his first calculations on the deflection of light by gravity. His solution was to think of an infinite number of inertial frames, each of which was instantaneously co-moving with the same linear velocity as the source. These co-moving frames are inertial and can be analyzed using the principles of special relativity. The general relativistic effects come from slipping from one inertial co-moving frame to the next. But in the case of the circular transverse Doppler effect, each instantaneously co-moving frame has the exact configuration as case A) above, and so the wavelength is red shifted exactly by the time dilation.

Fig. Left: Moving source around a stationary receiver has red-shifted light (pure time dilation effect). Right. Moving receiver around a stationary source has blue-shifted light.

E) Receiver in Circular Motion Around Source

Now flip the situation and consider a moving receiver orbiting a stationary source.

With the notion of co-moving inertial frames now in hand, this configuration is exactly the same as case B) above, and the wavelength is blue shifted according to the equation

caused by foreshortening.

By David D. Nolte, June 3, 2021

New from Oxford Press: The History of Light and Interference (2023)

Read about the physics and history of light and optics.

Available at Amazon

Available at Oxford

Available at Barnes&Noble

References

[1] A. Einstein, “On the electrodynamics of moving bodies,” Annalen Der Physik, vol. 17, no. 10, pp. 891-921, Sep (1905)

[2] D. D. Nolte, “The Fall and Rise of the Doppler Effect,” Physics Today, vol. 73, no. 3, pp. 31-35, Mar (2020)

[3] J. Stark, W. Hermann, and S. Kinoshita, “The Doppler effect in the spectrum of mercury,” Annalen Der Physik, vol. 21, pp. 462-469, Nov 1906.

[4] A. Einstein, “Possibility of a new examination of the relativity principle,” Annalen Der Physik, vol. 23, no. 6, pp. 197-198, May (1907)

[5] H. E. Ives and G. R. Stilwell, “An experimental study of the rate of a moving atomic clock,” Journal of the Optical Society of America, vol. 28, p. 215, 1938.

[6] B. Rossi and D. B. Hall, “Variation of the Rate of Decay of Mesotrons with Momentum,” Physical Review, vol. 59, pp. 223–228, 1941.

April 24, 2021October 23, 2023 by David D. Nolte

Hermann Minkowski’s Spacetime: The Theory that Einstein Overlooked

“Society is founded on hero worship”, wrote Thomas Carlyle (1795 – 1881) in his 1840 lecture on “Hero as Divinity”—and the society of physicists is no different. Among physicists, the hero is the genius—the monomyth who journeys into the supernatural realm of high mathematics, engages in single combat against chaos and confusion, gains enlightenment in the mysteries of the universe, and returns home to share the new understanding. If the hero is endowed with unusual talent and achieves greatness, then mythologies are woven, creating shadows that can grow and eclipse the truth and the work of others, bestowing upon the hero recognitions that are not entirely deserved.

“Gentlemen! The views of space and time which I wish to lay before you … They are radical. Henceforth space by itself, and time by itself, are doomed to fade away into mere shadows, and only a kind of union of the two will preserve an independent reality.”
Herman Minkowski (1908)

The greatest hero of physics of the twentieth century, without question, is Albert Einstein. He is the person most responsible for the development of “Modern Physics” that encompasses:

Relativity theory (both special and general),
Quantum theory (he invented the quantum in 1905—see my blog),
Astrophysics (his field equations of general relativity were solved by Schwarzschild in 1916 to predict event horizons of black holes, and he solved his own equations to predict gravitational waves that were discovered in 2015),
Cosmology (his cosmological constant is now recognized as the mysterious dark energy that was discovered in 2000), and
Solid state physics (his explanation of the specific heat of crystals inaugurated the field of quantum matter).

Einstein made so many seminal contributions to so many sub-fields of physics that it defies comprehension—hence he is mythologized as genius, able to see into the depths of reality with unique insight. He deserves his reputation as the greatest physicist of the twentieth century—he has my vote, and he was chosen by Time magazine in 2000 as the Man of the Century. But as his shadow has grown, it has eclipsed and even assimilated the work of others—work that he initially criticized and dismissed, yet later embraced so whole-heartedly that he is mistakenly given credit for its discovery.

For instance, when we think of Einstein, the first thing that pops into our minds is probably “spacetime”. He himself wrote several popular accounts of relativity that incorporated the view that spacetime is the natural geometry within which so many of the non-intuitive properties of relativity can be understood. When we think of time being mixed with space, making it seem that position coordinates and time coordinates share an equal place in the description of relativistic physics, it is common to attribute this understanding to Einstein. Yet Einstein initially resisted this viewpoint and even disparaged it when he first heard it!

Spacetime was the brain-child of Hermann Minkowski.

Minkowski in Königsberg

Hermann Minkowski was born in 1864 in Russia to German parents who moved to the city of Königsberg (King’s Mountain) in East Prussia when he was eight years old. He entered the university in Königsberg in 1880 when he was sixteen. Within a year, when he was only seventeen years old, and while he was still a student at the University, Minkowski responded to an announcement of the Mathematics Prize of the French Academy of Sciences in 1881. When he submitted is prize-winning memoire, he could have had no idea that it was starting him down a path that would lead him years later to revolutionary views.

A view of Königsberg in 1581. Six of the seven bridges of Königsberg—which Euler famously described in the first essay on topology—are seen in this picture. The University is in the center distance behind the castle. The city was destroyed by the Russians in WWII followed by a forced evacuation of the local population.

The specific Prize challenge of 1881 was to find the number of representations of an integer as a sum of five squares of integers. For instance, every integer n > 33 can be expressed as the sum of five nonzero squares. As an example, 42 = 2² + 2² + 3² + 3² + 4², which is the only representation for that number. However, there are five representation for n = 53

The task of enumerating these representations draws from the theory of quadratic forms. A quadratic form is a function of products of numbers with integer coefficients, such as ax² + bxy + cy² and ax² + by² + cz² + dxy + exz + fyz. In number theory, one seeks to find integer solutions for which the quadratic form equals an integer. For instance, the Pythagorean theorem x² + y² = n² for integers is a quadratic form for which there are many integer solutions (x,y,n), known as Pythagorean triplets, such as

The topic of quadratic forms gained special significance after the work of Bernhard Riemann who established the properties of metric spaces based on the metric expression

for infinitesimal distance in a D-dimensional metric space. This is a generalization of Euclidean distance to more general non-Euclidean spaces that may have curvature. Minkowski would later use this expression to great advantage, developing a “Geometry of Numbers” [1] as he delved ever deeper into quadratic forms and their uses in number theory.

Minkowski in Göttingen

After graduating with a doctoral degree in 1885 from Königsberg, Minkowski did his habilitation at the university of Bonn and began teaching, moving back to Königsberg in 1892 and then to Zurich in 1894 (where one of his students was a somewhat lazy and unimpressive Albert Einstein). A few years later he was given an offer that he could not refuse.

At the turn of the 20^th century, the place to be in mathematics was at the University of Göttingen. It had a long tradition of mathematical giants that included Carl Friedrich Gauss, Bernhard Riemann, Peter Dirichlet, and Felix Klein. Under the guidance of Felix Klein, Göttingen mathematics had undergone a renaissance. For instance, Klein had attracted Hilbert from the University of Königsberg in 1895. David Hilbert had known Minkowski when they were both students in Königsberg, and Hilbert extended an invitation to Minkowski to join him in Göttingen, which Minkowski accepted in 1902.

A few years after Minkowski arrived at Göttingen, the relativity revolution broke, and both Minkowski and Hilbert began working on mathematical aspects of the new physics. They organized a colloquium dedicated to relativity and related topics, and on Nov. 5, 1907 Minkowski gave his first tentative address on the geometry of relativity.

Because Minkowski’s specialty was quadratic forms, and given his understanding of Riemann’s work, he was perfectly situated to apply his theory of quadratic forms and invariants to the Lorentz transformations derived by Poincaré and Einstein. Although Poincaré had published a paper in 1906 that showed that the Lorentz transformation was a generalized rotation in four-dimensional space [2], Poincaré continued to discuss space and time as separate phenomena, as did Einstein. For them, simultaneity was no longer an invariant, but events in time were still events in time and not somehow mixed with space-like properties. Minkowski recognized that Poincaré had missed an opportunity to define a four-dimensional vector space filled by four-vectors that captured all possible events in a single coordinate description without the need to separate out time and space.

Minkowski’s first attempt, presented in his 1907 colloquium, at constructing velocity four-vectors was flawed because (like so many of my mechanics students when they first take a time derivative of the four-position) he had not yet understood the correct use of proper time. But the research program he outlined paved the way for the great work that was to follow.

On Feb. 21, 1908, only 3 months after his first halting steps, Minkowski delivered a thick manuscript to the printers for an article to appear in the Göttinger Nachrichten. The title “Die Grundgleichungen für die elektromagnetischen Vorgänge in bewegten Körpern” (The Basic Equations for Electromagnetic Processes of Moving Bodies) belies the impact and importance of this very dense article [3]. In its 60 pages (with no figures), Minkowski presents the correct form for four-velocity by taking derivatives relative to proper time, and he formalizes his four-dimensional approach to relativity that became the standard afterwards. He introduces the terms spacelike vector, timelike vector, light cone and world line. He also presents the complete four-tensor form for the electromagnetic fields. The foundational work of Levi Cevita and Ricci-Curbastro on tensors was not yet well known, so Minkowski invents his own terminology of Traktor to describe it. Most importantly, he invents the terms spacetime (Raum-Zeit) and events (Erignisse) [4].

Minkowski’s four-dimensional formalism of relativistic electromagnetics was more than a mathematical trick—it uncovered the presence of a multitude of invariants that were obscured by the conventional mathematics of Einstein and Lorentz and Poincaré. In Minkowski’s approach, whenever a proper four-vector is contracted with itself (its inner product), an invariant emerges. Because there are many fundamental four-vectors, there are many invariants. These invariants provide the anchors from which to understand the complex relative properties amongst relatively moving frames.

Minkowski’s master work appeared in the Nachrichten on April 5, 1908. If he had thought that physicists would embrace his visionary perspective, he was about to be woefully disabused of that notion.

Einstein’s Reaction

Despite his impressive ability to see into the foundational depths of the physical world, Einstein did not view mathematics as the root of reality. Mathematics for him was a tool to reduce physical intuition into quantitative form. In 1908 his fame was rising as the acknowledged leader in relativistic physics, and he was not impressed or pleased with the abstract mathematical form that Minkowski was trying to stuff the physics into. Einstein called it “superfluous erudition” [5], and complained “since the mathematics pounced on the relativity theory, I no longer understand it myself! [6]”

With his collaborator Jakob Laub (also a former student of Minkowski’s), Einstein objected to more than the hard-to-follow mathematics—they believed that Minkowski’s form of the pondermotive force was incorrect. They then proceeded to re-translate Minkowski’s elegant four-vector derivations back into ordinary vector analysis, publishing two papers in Annalen der Physik in the summer of 1908 that were politely critical of Minkowski’s approach [7-8]. Yet another of Minkowski’s students from Zurich, Gunnar Nordström, showed how to derive Minkowski’s field equations without any of the four-vector formalism.

One can only wonder why so many of his former students so easily dismissed Minkowski’s revolutionary work. Einstein had actually avoided Minkowski’s mathematics classes as a student at ETH [5], which may say something about Minkowski’s reputation among the students, although Einstein did appreciate the class on mechanics that he took from Minkowski. Nonetheless, Einstein missed the point! Rather than realizing the power and universality of the four-dimensional spacetime formulation, he dismissed it as obscure and irrelevant—perhaps prejudiced by his earlier dim view of his former teacher.

Raum und Zeit

It is clear that Minkowski was stung by the poor reception of his spacetime theory. It is also clear that he truly believed that he had uncovered an essential new approach to physical reality. While mathematicians were generally receptive of his work, he knew that if physicists were to adopt his new viewpoint, he needed to win them over with the elegant results.

In 1908, Minkowski presented a now-famous paper Raum und Zeit at the 80^th Assembly of German Natural Scientists and Physicians (21 September 1908). In his opening address, he stated [9]:

“Gentlemen! The views of space and time which I wish to lay before you have sprung from the soil of experimental physics, and therein lies their strength. They are radical. Henceforth space by itself, and time by itself, are doomed to fade away into mere shadows, and only a kind of union of the two will preserve an independent reality.”

To illustrate his arguments Minkowski constructed the most recognizable visual icon of relativity theory—the space-time diagram in which the trajectories of particles appear as “world lines”, as in Fig. 1. On this diagram, one spatial dimension is plotted along the horizontal-axis, and the value ct (speed of light times time) is plotted along the vertical-axis. In these units, a photon travels along a line oriented at 45 degrees, and the world-line (the name Minkowski gave to trajectories) of all massive particles must have slopes steeper than this. For instance, a stationary particle, that appears to have no trajectory at all, executes a vertical trajectory on the space-time diagram as it travels forward through time. Within this new formulation by Minkowski, space and time were mixed together in a single manifold—spacetime—and were no longer separate entities.

Fig. 1 The First “Minkowski diagram” of spacetime.

In addition to the spacetime construct, Minkowski’s great discovery was the plethora of invariants that followed from his geometry. For instance, the spacetime hyperbola

is invariant to Lorentz transformation in coordinates. This is just a simple statement that a vector is an entity of reality that is independent of how it is described. The length of a vector in our normal three-space does not change if we flip the coordinates around or rotate them, and the same is true for four-vectors in Minkowski space subject to Lorentz transformations.

In relativity theory, this property of invariance becomes especially useful because part of the mental challenge of relativity is that everything looks different when viewed from different frames. How do you get a good grip on a phenomenon if it is always changing, always relative to one frame or another? The invariants become the anchors that we can hold on to as reference frames shift and morph about us.

Fig. 2 Any event on an invariant hyperbola is transformed by the Lorentz transformation onto another point on the same hyperbola. Events that are simultaneous in one frame are each on a separate hyperbola. After transformation, simultaneity is lost, but each event stays on its own invariant hyperbola (Figure reprinted from [10]).

As an example of a fundamental invariant, the mass of a particle in its rest frame becomes an invariant mass, always with the same value. In earlier relativity theory, even in Einstein’s papers, the mass of an object was a function of its speed. How is the mass of an electron a fundamental property of physics if it is a function of how fast it is traveling? The construction of invariant mass removes this problem, and the mass of the electron becomes an immutable property of physics, independent of the frame. Invariant mass is just one of many invariants that emerge from Minkowski’s space-time description. The study of relativity, where all things seem relative, became a study of invariants, where many things never change. In this sense, the theory of relativity is a misnomer. Ironically, relativity theory became the motivation of post-modern relativism that denies the existence of absolutes, even as relativity theory, as practiced by physicists, is all about absolutes.

Despite his audacious gambit to win over the physicists, Minkowski would not live to see the fruits of his effort. He died suddenly of a burst gall bladder on Jan. 12, 1909 at the age of 44.

Arnold Sommerfeld (who went on to play a central role in the development of quantum theory) took up Minkowski’s four vectors, and he systematized it in a way that was palatable to physicists. Then Max von Laue extended it while he was working with Sommerfeld in Munich, publishing the first physics textbook on relativity theory in 1911, establishing the space-time formalism for future generations of German physicists. Further support for Minkowski’s work came from his distinguished colleagues at Göttingen (Hilbert, Klein, Wiechert, Schwarzschild) as well as his former students (Born, Laue, Kaluza, Frank, Noether). With such champions, Minkowski’s work was immortalized in the methodology (and mythology) of physics, representing one of the crowning achievements of the Göttingen mathematical community.

Einstein Relents

Already in 1907 Einstein was beginning to grapple with the role of gravity in the context of relativity theory, and he knew that the special theory was just a beginning. Yet between 1908 and 1910 Einstein’s focus was on the quantum of light as he defended and extended his unique view of the photon and prepared for the first Solvay Congress of 1911. As he returned his attention to the problem of gravitation after 1910, he began to realize that Minkowski’s formalism provided a framework from which to understand the role of accelerating frames. In 1912 Einstein wrote to Sommerfeld to say [5]

I occupy myself now exclusively with the problem of gravitation . One thing is certain that I have never before had to toil anywhere near as much, and that I have been infused with great respect for mathematics, which I had up until now in my naivety looked upon as a pure luxury in its more subtle parts. Compared to this problem. the original theory of relativity is child’s play.

By the time Einstein had finished his general theory of relativity and gravitation in 1915, he fully acknowledge his indebtedness to Minkowski’s spacetime formalism without which his general theory may never have appeared.

By David D. Nolte, April 24, 2021

[1] H. Minkowski, Geometrie der Zahlen. Leipzig and Berlin: R. G. Teubner, 1910.

[2] Poincaré, H. (1906). “Sur la dynamique de l’´electron.” Rendiconti del circolo matematico di Palermo 21: 129–176.

[3] H. Minkowski, “Die Grundgleichungen für die electromagnetischen Vorgänge in bewegten Körpern,” Nachrichten von der Königlichen Gesellschaft der Wissenschaften zu Göttingen, pp. 53–111, (1908)

[4] S. Walter, “Minkowski’s Modern World,” in Minkowski Spacetime: A Hundred Years Later, Petkov Ed.: Springer, 2010, ch. 2, pp. 43-61.

[5] L. Corry, “The influence of David Hilbert and Hermann Minkowski on Einstein’s views over the interrelation between physics and mathematics,” Endeavour, vol. 22, no. 3, pp. 95-97, (1998)

[6] A. Pais, Subtle is the Lord: The Science and the Life of Albert Einstein. Oxford, 2005.

[7] A. Einstein and J. Laub, “Electromagnetic basic equations for moving bodies,” Annalen Der Physik, vol. 26, no. 8, pp. 532-540, Jul (1908)

[8] A. Einstein and J. Laub, “Electromagnetic fields on quiet bodies with pondermotive energy,” Annalen Der Physik, vol. 26, no. 8, pp. 541-550, Jul (1908)

[9] Minkowski, H. (1909). “Raum und Zeit.” Jahresbericht der Deutschen Mathematikier-Vereinigung: 75-88.

[10] D. D. Nolte, Introduction to Modern Dynamics : Chaos, Networks, Space and Time, 2nd ed. Oxford: Oxford University Press, 2019.

Interference (New from Oxford University Press, 2023)

Read the stories of the scientists and engineers who tamed light and used it to probe the universe.

Available from Amazon.

Available from Oxford U Press

Available from Barnes & Nobles