The first time I ran across the Bohr-Sommerfeld quantization conditions I admit that I laughed! I was a TA for the Modern Physics course as a graduate student at Berkeley in 1982 and I read about Bohr-Sommerfeld in our Tipler textbook. I was familiar with Bohr orbits, which are already the wrong way of thinking about quantized systems. So the Bohr-Sommerfeld conditions, especially for so-called “elliptical” orbits, seemed like nonsense.
But it’s funny how a a little distance gives you perspective. Forty years later I know a little more physics than I did then, and I have gained a deep respect for an obscure property of dynamical systems known as “adiabatic invariants”. It turns out that adiabatic invariants lie at the core of quantum systems, and in the case of hydrogen adiabatic invariants can be visualized as … elliptical orbits!
Quantum Physics in Copenhagen
Niels Bohr (1885 – 1962) was born in Copenhagen, Denmark, the middle child of a physiology professor at the University in Copenhagen. Bohr grew up with his siblings as a faculty child, which meant an unconventional upbringing full of ideas, books and deep discussions. Bohr was a late bloomer in secondary school but began to show talent in Math and Physics in his last two years. When he entered the University in Copenhagen in 1903 to major in physics, the university had only one physics professor, Christian Christiansen, and had no physics laboratories. So Bohr tinkered in his father’s physiology laboratory, performing a detailed experimental study of the hydrodynamics of water jets, writing and submitting a paper that was to be his only experimental work. Bohr went on to receive a Master’s degree in 1909 and his PhD in 1911, writing his thesis on the theory of electrons in metals. Although the thesis did not break much new ground, it uncovered striking disparities between observed properties and theoretical predictions based on the classical theory of the electron. For his postdoc studies he applied for and was accepted to a position working with the discoverer of the electron, Sir J. J. Thompson, in Cambridge. Perhaps fortunately for the future history of physics, he did not get along well with Thompson, and he shifted his postdoc position in early 1912 to work with Ernest Rutherford at the much less prestigious University of Manchester.

Ernest Rutherford had just completed a series of detailed experiments on the scattering of alpha particles on gold film and had demonstrated that the mass of the atom was concentrated in a very small volume that Rutherford called the nucleus, which also carried the positive charge compensating the negative electron charges. The discovery of the nucleus created a radical new model of the atom in which electrons executed planetary-like orbits around the nucleus. Bohr immediately went to work on a theory for the new model of the atom. He worked closely with Rutherford and the other members of Rutherford’s laboratory, involved in daily discussions on the nature of atomic structure. The open intellectual atmosphere of Rutherford’s group and the ready flow of ideas in group discussions became the model for Bohr, who would some years later set up his own research center that would attract the top young physicists of the time. Already by mid 1912, Bohr was beginning to see a path forward, hinting in letters to his younger brother Harald (who would become a famous mathematician) that he had uncovered a new approach that might explain some of the observed properties of simple atoms.
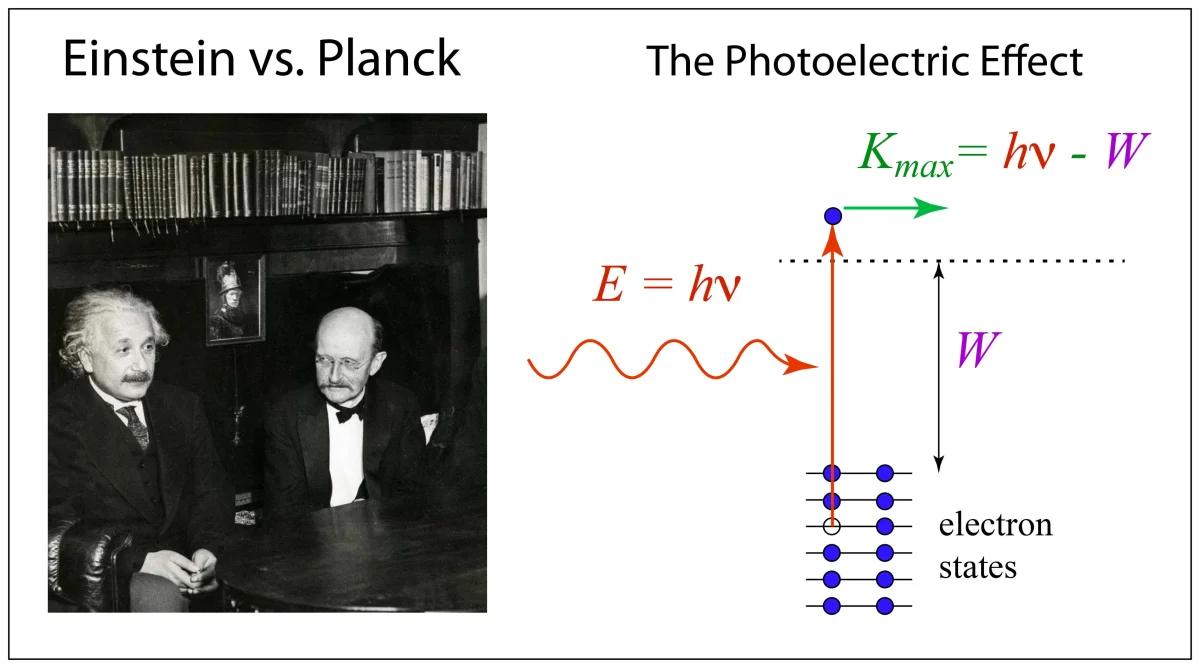
By the end of 1912 his postdoc travel stipend was over, and he returned to Copenhagen, where he completed his work on the hydrogen atom. One of the key discrepancies in the classical theory of the electron in atoms was the requirement, by Maxwell’s Laws, for orbiting electrons to continually radiate because of their angular acceleration. Furthermore, from energy conservation, if they radiated continuously, the electron orbits must also eventually decay into the nuclear core with ever-decreasing orbital periods and hence ever higher emitted light frequencies. Experimentally, on the other hand, it was known that light emitted from atoms had only distinct quantized frequencies. To circumvent the problem of classical radiation, Bohr simply assumed what was observed, formulating the idea of stationary quantum states. Light emission (or absorption) could take place only when the energy of an electron changed discontinuously as it jumped from one stationary state to another, and there was a lowest stationary state below which the electron could never fall. He then took a critical and important step, combining this new idea of stationary states with Planck’s constant h. He was able to show that the emission spectrum of hydrogen, and hence the energies of the stationary states, could be derived if the angular momentum of the electron in a Hydrogen atom was quantized by integer amounts of Planck’s constant h.
Bohr published his quantum theory of the hydrogen atom in 1913, which immediately focused the attention of a growing group of physicists (including Einstein, Rutherford, Hilbert, Born, and Sommerfeld) on the new possibilities opened up by Bohr’s quantum theory [1]. Emboldened by his growing reputation, Bohr petitioned the university in Copenhagen to create a new faculty position in theoretical physics, and to appoint him to it. The University was not unreceptive, but university bureaucracies make decisions slowly, so Bohr returned to Rutherford’s group in Manchester while he awaited Copenhagen’s decision. He waited over two years, but he enjoyed his time in the stimulating environment of Rutherford’s group in Manchester, growing steadily into the role as master of the new quantum theory. In June of 1916, Bohr returned to Copenhagen and a year later was elected to the Royal Danish Academy of Sciences.
Although Bohr’s theory had succeeded in describing some of the properties of the electron in atoms, two central features of his theory continued to cause difficulty. The first was the limitation of the theory to single electrons in circular orbits, and the second was the cause of the discontinuous jumps. In response to this challenge, Arnold Sommerfeld provided a deeper mechanical perspective on the origins of the discrete energy levels of the atom.
Quantum Physics in Munich
Arnold Johannes Wilhem Sommerfeld (1868—1951) was born in Königsberg, Prussia, and spent all the years of his education there to his doctorate that he received in 1891. In Königsberg he was acquainted with Minkowski, Wien and Hilbert, and he was the doctoral student of Lindemann. He also was associated with a social group at the University that spent too much time drinking and dueling, a distraction that lead to his receiving a deep sabre cut on his forehead that became one of his distinguishing features along with his finely waxed moustache. In outward appearance, he looked the part of a Prussian hussar, but he finally escaped this life of dissipation and landed in Göttingen where he became Felix Klein’s assistant in 1894. He taught at local secondary schools, rising in reputation, until he secured a faculty position of theoretical physics at the University in Münich in 1906. One of his first students was Peter Debye who received his doctorate under Sommerfeld in 1908. Later famous students would include Peter Ewald (doctorate in 1912), Wolfgang Pauli (doctorate in 1921), Werner Heisenberg (doctorate in 1923), and Hans Bethe (doctorate in 1928). These students had the rare treat, during their time studying under Sommerfeld, of spending weekends in the winter skiing and staying at a ski hut that he owned only two hours by train outside of Münich. At the end of the day skiing, discussion would turn invariably to theoretical physics and the leading problems of the day. It was in his early days at Münich that Sommerfeld played a key role aiding the general acceptance of Minkowski’s theory of four-dimensional space-time by publishing a review article in Annalen der Physik that translated Minkowski’s ideas into language that was more familiar to physicists.
Around 1911, Sommerfeld shifted his research interest to the new quantum theory, and his interest only intensified after the publication of Bohr’s model of hydrogen in 1913. In 1915 Sommerfeld significantly extended the Bohr model by building on an idea put forward by Planck. While further justifying the black body spectrum, Planck turned to descriptions of the trajectory of a quantized one-dimensional harmonic oscillator in phase space. Planck had noted that the phase-space areas enclosed by the quantized trajectories were integral multiples of his constant. Sommerfeld expanded on this idea, showing that it was not the area enclosed by the trajectories that was fundamental, but the integral of the momentum over the spatial coordinate [2]. This integral is none other than the original action integral of Maupertuis and Euler, used so famously in their Principle of Least Action almost 200 years earlier. Where Planck, in his original paper of 1901, had recognized the units of his constant to be those of action, and hence called it the quantum of action, Sommerfeld made the explicit connection to the dynamical trajectories of the oscillators. He then showed that the same action principle applied to Bohr’s circular orbits for the electron on the hydrogen atom, and that the orbits need not even be circular, but could be elliptical Keplerian orbits.
The quantum condition for this otherwise classical trajectory was the requirement for the action integral over the motion to be equal to integer units of the quantum of action. Furthermore, Sommerfeld showed that there must be as many action integrals as degrees of freedom for the dynamical system. In the case of Keplerian orbits, there are radial coordinates as well as angular coordinates, and each action integral was quantized for the discrete electron orbits. Although Sommerfeld’s action integrals extended Bohr’s theory of quantized electron orbits, the new quantum conditions also created a problem because there were now many possible elliptical orbits that all had the same energy. How was one to find the “correct” orbit for a given orbital energy?
Quantum Physics in Leiden
In 1906, the Austrian Physicist Paul Ehrenfest (1880 – 1933), freshly out of his PhD under the supervision of Boltzmann, arrived at Göttingen only weeks before Boltzmann took his own life. Felix Klein at Göttingen had been relying on Boltzmann to provide a comprehensive review of statistical mechanics for the Mathematical Encyclopedia, so he now entrusted this project to the young Ehrenfest. It was a monumental task, which was to take him and his physicist wife Tatyana nearly five years to complete. Part of the delay was the desire by Ehrenfest to close some open problems that remained in Boltzmann’s work. One of these was a mechanical theorem of Boltzmann’s that identified properties of statistical mechanical systems that remained unaltered through a very slow change in system parameters. These properties would later be called adiabatic invariants by Einstein. Ehrenfest recognized that Wien’s displacement law, which had been a guiding light for Planck and his theory of black body radiation, had originally been derived by Wien using classical principles related to slow changes in the volume of a cavity. Ehrenfest was struck by the fact that such slow changes would not induce changes in the quantum numbers of the quantized states, and hence that the quantum numbers must be adiabatic invariants of the black body system. This not only explained why Wien’s displacement law continued to hold under quantum as well as classical considerations, but it also explained why Planck’s quantization of the energy of his simple oscillators was the only possible choice. For a classical harmonic oscillator, the ratio of the energy of oscillation to the frequency of oscillation is an adiabatic invariant, which is immediately recognized as Planck’s quantum condition .

Ehrenfest published his observations in 1913 [3], the same year that Bohr published his theory of the hydrogen atom, so Ehrenfest immediately applied the theory of adiabatic invariants to Bohr’s model and discovered that the quantum condition for the quantized energy levels was again the adiabatic invariants of the electron orbits, and not merely a consequence of integer multiples of angular momentum, which had seemed somewhat ad hoc. Later, when Sommerfeld published his quantized elliptical orbits in 1916, the multiplicity of quantum conditions and orbits had caused concern, but Ehrenfest came to the rescue with his theory of adiabatic invariants, showing that each of Sommerfeld’s quantum conditions were precisely the adabatic invariants of the classical electron dynamics [4]. The remaining question was which coordinates were the correct ones, because different choices led to different answers. This was quickly solved by Johannes Burgers (one of Ehrenfest’s students) who showed that action integrals were adiabatic invariants, and then by Karl Schwarzschild and Paul Epstein who showed that action-angle coordinates were the only allowed choice of coordinates, because they enabled the separation of the Hamilton-Jacobi equations and hence provided the correct quantization conditions for the electron orbits. Schwarzshild’s paper was published the same day that he died on the Eastern Front. The work by Schwarzschild and Epstein was the first to show the power of the Hamiltonian formulation of dynamics for quantum systems, which foreshadowed the future importance of Hamiltonians for quantum theory.

Bohr-Sommerfeld
Emboldened by Ehrenfest’s adiabatic principle, which demonstrated a close connection between classical dynamics and quantization conditions, Bohr formalized a technique that he had used implicitly in his 1913 model of hydrogen, and now elevated it to the status of a fundamental principle of quantum theory. He called it the Correspondence Principle, and published the details in 1920. The Correspondence Principle states that as the quantum number of an electron orbit increases to large values, the quantum behavior converges to classical behavior. Specifically, if an electron in a state of high quantum number emits a photon while jumping to a neighboring orbit, then the wavelength of the emitted photon approaches the classical radiation wavelength of the electron subject to Maxwell’s equations.
Bohr’s Correspondence Principle cemented the bridge between classical physics and quantum physics. One of the biggest former questions about the physics of electron orbits in atoms was why they did not radiate continuously because of the angular acceleration they experienced in their orbits. Bohr had now reconnected to Maxwell’s equations and classical physics in the limit. Like the theory of adiabatic invariants, the Correspondence Principle became a new tool for distinguishing among different quantum theories. It could be used as a filter to distinguish “correct” quantum models, that transitioned smoothly from quantum to classical behavior, from those that did not. Bohr’s Correspondence Principle was to be a powerful tool in the hands of Werner Heisenberg as he reinvented quantum theory only a few years later.

By the end of 1920, all the elements of the quantum theory of electron orbits were apparently falling into place. Bohr’s originally ad hoc quantization condition was now on firm footing. The quantization conditions were related to action integrals that were, in turn, adiabatic invariants of the classical dynamics. This meant that slight variations in the parameters of the dynamics systems would not induce quantum transitions among the various quantum states. This conclusion would have felt right to the early quantum practitioners. Bohr’s quantum model of electron orbits was fundamentally a means of explaining quantum transitions between stationary states. Now it appeared that the condition for the stationary states of the electron orbits was an insensitivity, or invariance, to variations in the dynamical properties. This was analogous to the principle of stationary action where the action along a dynamical trajectory is invariant to slight variations in the trajectory. Therefore, the theory of quantum orbits now rested on firm foundations that seemed as solid as the foundations of classical mechanics.
From the perspective of modern quantum theory, the concept of elliptical Keplerian orbits for the electron is grossly inaccurate. Most physicists shudder when they see the symbol for atomic energy—the classic but mistaken icon of electron orbits around a nucleus. Nonetheless, Bohr and Ehrenfest and Sommerfeld had hit on a deep thread that runs through all of physics—the concept of action—the same concept that Leibniz introduced, that Maupertuis minimized and that Euler canonized. This concept of action is at work in the macroscopic domain of classical dynamics as well as the microscopic world of quantum phenomena. Planck was acutely aware of this connection with action, which is why he so readily recognized his elementary constant as the quantum of action.
However, the old quantum theory was running out of steam. For instance, the action integrals and adiabatic invariants only worked for single electron orbits, leaving the vast bulk of many-electron atomic matter beyond the reach of quantum theory and prediction. The literal electron orbits were a crutch or bias that prevented physicists from moving past them and seeing new possibilities for quantum theory. Orbits were an anachronism, exerting a damping force on progress. This limitation became painfully clear when Bohr and his assistants at Copenhagen–Kramers and Slater–attempted to use their electron orbits to explain the refractive index of gases. The theory was cumbersome and exhausted. It was time for a new quantum revolution by a new generation of quantum wizards–Heisenberg, Born, Schrödinger, Pauli, Jordan and Dirac.
References
[1] N. Bohr, “On the Constitution of Atoms and Molecules, Part II Systems Containing Only a Single Nucleus,” Philosophical Magazine, vol. 26, pp. 476–502, 1913.
[2] A. Sommerfeld, “The quantum theory of spectral lines,” Annalen Der Physik, vol. 51, pp. 1-94, Sep 1916.
[3] P. Ehrenfest, “Een mechanische theorema van Boltzmann en zijne betrekking tot de quanta theorie (A mechanical theorem of Boltzmann and its relation to the theory of energy quanta),” Verslag van de Gewoge Vergaderingen der Wis-en Natuurkungige Afdeeling, vol. 22, pp. 586-593, 1913.
[4] P. Ehrenfest, “Adiabatic invariables and quantum theory,” Annalen Der Physik, vol. 51, pp. 327-352, Oct 1916.