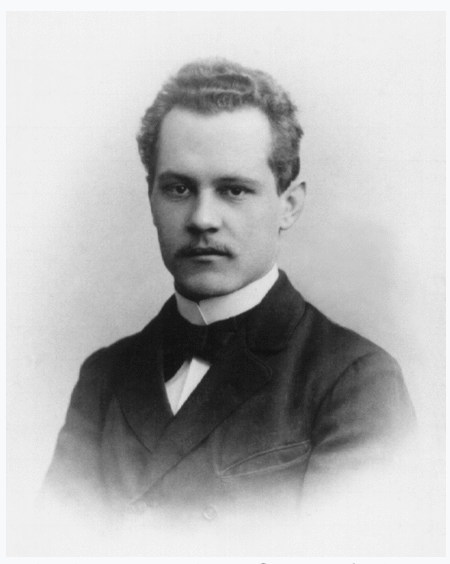Despite the many apparent paradoxes posed in physics—the twin and ladder paradoxes of relativity theory, Olber’s paradox of the bright night sky, Loschmitt’s paradox of irreversible statistical fluctuations—these are resolved by a deeper look at the underlying assumptions—the twin paradox is resolved by considering shifts in reference frames, the ladder paradox is resolved by the loss of simultaneity, Olber’s paradox is resolved by a finite age to the universe, and Loschmitt’s paradox is resolved by fluctuation theorems. In each case, no physical principle is violated, and each paradox is fully explained.
However, there is at least one “true” paradox in physics that defies consistent explanation—quantum entanglement. Quantum entanglement was first described by Einstein with colleagues Podolsky and Rosen in the famous EPR paper of 1935 as an argument against the completeness of quantum mechanics, and it was given its name by Schrödinger the same year in the paper where he introduced his “cat” as a burlesque consequence of entanglement.
Here is a short history of quantum entanglement [1], from its beginnings in 1935 to the recent 2022 Nobel prize in Physics awarded to John Clauser, Alain Aspect and Anton Zeilinger.
The EPR Papers of 1935
Einstein can be considered as the father of quantum mechanics, even over Planck, because of his 1905 derivation of the existence of the photon as a discrete carrier of a quantum of energy (see Einstein versus Planck). Even so, as Heisenberg and Bohr advanced quantum mechanics in the mid 1920’s, emphasizing the underlying non-deterministic outcomes of measurements, and in particular the notion of instantaneous wavefunction collapse, they pushed the theory in directions that Einstein found increasingly disturbing and unacceptable.
This feature is an excerpt from an upcoming book, Interference: The History of Optical Interferometry and the Scientists Who Tamed Light (Oxford University Press, July 2023), by David D. Nolte.
At the invitation-only Solvay Congresses of 1927 and 1930, where all the top physicists met to debate the latest advances, Einstein and Bohr began a running debate that was epic in the history of physics as the two top minds went head-to-head as the onlookers looked on in awe. Ultimately, Einstein was on the losing end. Although he was convinced that something was missing in quantum theory, he could not counter all of Bohr’s rejoinders, even as Einstein’s assaults became ever more sophisticated, and he left the field of battle beaten but not convinced. Several years later he launched his last and ultimate salvo.

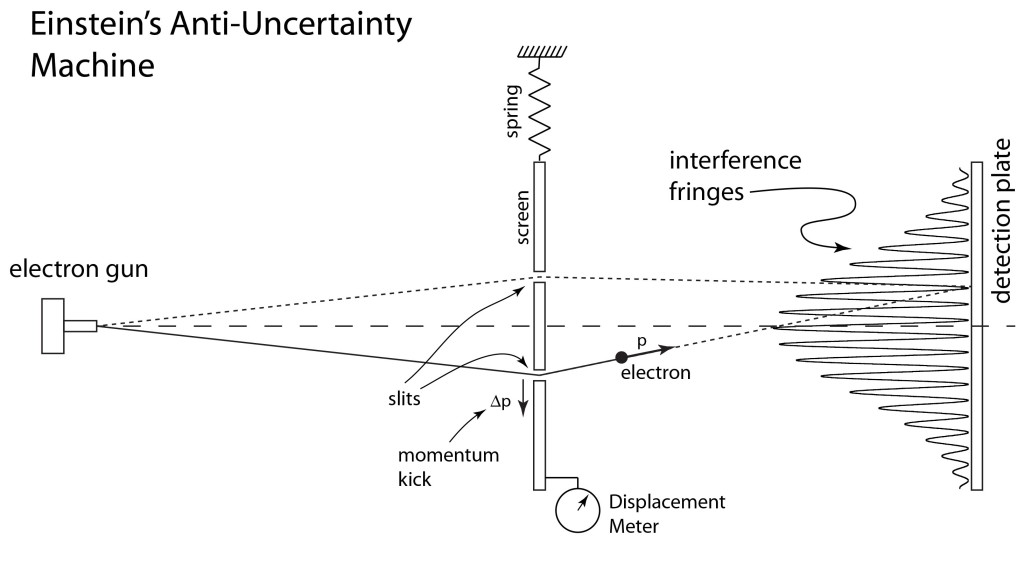
At the Institute for Advanced Study in Princeton, New Jersey, in the 1930’s Einstein was working with Nathan Rosen and Boris Podolsky when he envisioned a fundamental paradox in quantum theory that occurred when two widely-separated quantum particles were required to share specific physical properties because of simple conservation theorems like energy and momentum. Even Bohr and Heisenberg could not deny the principle of conservation of energy and momentum, and Einstein devised a two-particle system for which these conservation principles led to an apparent violation of Heisenberg’s own uncertainty principle. He left the details to his colleagues, with Podolsky writing up the main arguments. They published the paper in the Physical Review in March of 1935 with the title “Can Quantum-Mechanical Description of Physical Reality be Considered Complete” [2]. Because of the three names on the paper (Einstein, Podolsky, Rosen), it became known as the EPR paper, and the paradox they presented became known as the EPR paradox.
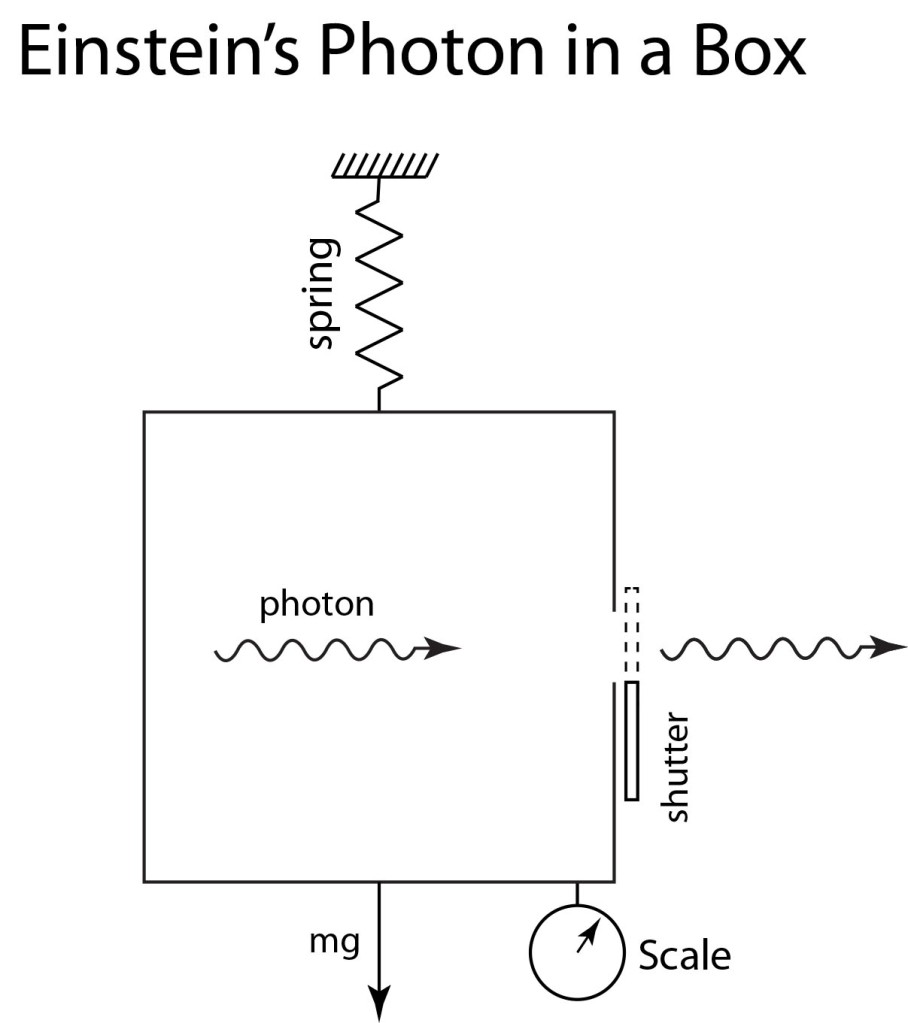
When Bohr read the paper, he was initially stumped and aghast. He felt that EPR had shaken the very foundations of the quantum theory that he and his institute had fought so hard to establish. He also suspected that EPR had made a mistake in their arguments, and he halted all work at his institute in Copenhagen until they could construct a definitive answer. A few months later, Bohr published a paper in the Physical Review in July of 1935, using the identical title that EPR had used, in which he refuted the EPR paradox [3]. There is not a single equation or figure in the paper, but he used his “awful incantation terminology” to maximum effect, showing that one of the EPR assumptions on the assessment of uncertainties to position and momentum was in error, and he was right.
Einstein was disgusted. He had hoped that this ultimate argument against the completeness of quantum mechanics would stand the test of time, but Bohr had shot it down within mere months. Einstein was particularly disappointed with Podolsky, because Podolsky had tried too hard to make the argument specific to position and momentum, leaving a loophole for Bohr to wiggle through, where Einstein had wanted the argument to rest on deeper and more general principles.
Despite Bohr’s victory, Einstein had been correct in his initial formulation of the EPR paradox that showed quantum mechanics did not jibe with common notions of reality. He and Schrödinger exchanged letters commiserating with each other and encouraging each other in their counter beliefs against Bohr and Heisenberg. In November of 1935, Schrödinger published a broad, mostly philosophical, paper in Naturwissenschaften [4] in which he amplified the EPR paradox with the use of an absurd—what he called burlesque—consequence of wavefunction collapse that became known as Schrödinger’s Cat. He also gave the central property of the EPR paradox its name: entanglement.
Ironically, both Einstein’s entanglement paradox and Schrödinger’s Cat, which were formulated originally to be arguments against the validity of quantum theory, have become established quantum tools. Today, entangled particles are the core workhorses of quantum information systems, and physicists are building larger and larger versions of Schrödinger’s Cat that may eventually merge with the physics of the macroscopic world.
Bohm and Ahronov Tackle EPR
The physicist David Bohm was a rare political exile from the United States. He was born in the heart of Pennsylvania in the town of Wilkes-Barre, attended Penn State and then the University of California at Berkeley, where he joined Robert Oppenheimer’s research group. While there, he became deeply involved in the fight for unions and socialism, activities for which he was called before McCarthy’s Committee on Un-American Activities. He invoked his right to the fifth amendment for which he was arrested. Although he was later acquitted, Princeton University fired him from his faculty position, and fearing another arrest, he fled to Brazil where his US passport was confiscated by American authorities. He had become a physicist without a country.

Despite his personal trials, Bohm remained scientifically productive. He published his influential textbook on quantum mechanics in the midst of his Senate hearings, and after a particularly stimulating discussion with Einstein shortly before he fled the US, he developed and published an alternative version of quantum theory in 1952 that was fully deterministic—removing Einstein’s “God playing dice”—by creating a hidden-variable theory [5].
Hidden-variable theories of quantum mechanics seek to remove the randomness of quantum measurement by assuming that some deeper element of quantum phenomena—a hidden variable—explains each outcome. But it is also assumed that these hidden variables are not directly accessible to experiment. In this sense, the quantum theory of Bohr and Heisenberg was “correct” but not “complete”, because there were things that the theory could not predict or explain.
Bohm’s hidden variable theory, based on a quantum potential, was able to reproduce all the known results of standard quantum theory without invoking the random experimental outcomes that Einstein abhorred. However, it still contained one crucial element that could not sweep away the EPR paradox—it was nonlocal.
Nonlocality lies at the heart of quantum theory. In its simplest form, the nonlocal nature of quantum phenomenon says that quantum states span spacetime with space-like separations, meaning that parts of the wavefunction are non-causally connected to other parts of the wavefunction. Because Einstein was fundamentally committed to causality, the nonlocality of quantum theory was what he found most objectionable, and Bohm’s elegant hidden-variable theory, that removed Einstein’s dreaded randomness, could not remove that last objection of non-causality.
After working in Brazil for several years, Bohm moved to the Technion University in Israel where he began a fruitful collaboration with Yakir Ahronov. In addition to proposing the Ahronov-Bohm effect, in 1957 they reformulated Podolsky’s version of the EPR paradox that relied on continuous values of position and momentum and replaced it with a much simpler model based on the Stern-Gerlach effect on spins and further to the case of positronium decay into two photons with correlated polarizations. Bohm and Ahronov reassessed experimental results of positronium decay that had been made by Madame Wu in 1950 at Columbia University and found it in full agreement with standard quantum theory.
John Bell’s Inequalities
John Stuart Bell had an unusual start for a physicist. His family was too poor to give him an education appropriate to his skills, so he enrolled in vocational school where he took practical classes that included brick laying. Working later as a technician in a university lab, he caught the attention of his professors who sponsored him to attend the university. With a degree in physics, he began working at CERN as an accelerator designer when he again caught the attention of his supervisors who sponsored him to attend graduate school. He graduated with a PhD and returned to CERN as a card-carrying physicist with all the rights and privileges that entailed.

During his university days, he had been fascinated by the EPR paradox, and he continued thinking about the fundamentals of quantum theory. On a sabbatical to the Stanford accelerator in 1960 he began putting mathematics to the EPR paradox to see whether any local hidden variable theory could be compatible with quantum mechanics. His analysis was fully general, so that it could rule out as-yet-unthought-of hidden-variable theories. The result of this work was a set of inequalities that must be obeyed by any local hidden-variable theory. Then he made a simple check using the known results of quantum measurement and showed that his inequalities are violated by quantum systems. This ruled out the possibility of any local hidden variable theory (but not Bohm’s nonlocal hidden-variable theory). Bell published his analysis in 1964 [6] in an obscure journal that almost no one read…except for a curious graduate student at Columbia University who began digging into the fundamental underpinnings of quantum theory against his supervisor’s advice.

John Clauser’s Tenacious Pursuit
As a graduate student in astrophysics at Columbia University, John Clauser was supposed to be doing astrophysics. Instead, he spent his time musing over the fundamentals of quantum theory. In 1967 Clauser stumbled across Bell’s paper while he was in the library. The paper caught his imagination, but he also recognized that the inequalities were not experimentally testable, because they required measurements that depended directly on hidden variables, which are not accessible. He began thinking of ways to construct similar inequalities that could be put to an experimental test, and he wrote about his ideas to Bell, who responded with encouragement. Clauser wrote up his ideas in an abstract for an upcoming meeting of the American Physical Society, where one of the abstract reviewers was Abner Shimony of Boston University. Clauser was surprised weeks later when he received a telephone call from Shimony. Shimony and his graduate student Micheal Horne had been thinking along similar lines, and Shimony proposed to Clauser that they join forces. They met in Boston where they were met Richard Holt, a graudate student at Harvard who was working on experimental tests of quantum mechanics. Collectively, they devised a new type of Bell inequality that could be put to experimental test [7]. The result has become known as the CHSH Bell inequality (after Clauser, Horne, Shimony and Holt).

When Clauser took a post-doc position in Berkeley, he began searching for a way to do the experiments to test the CHSH inequality, even though Holt had a head start at Harvard. Clauser enlisted the help of Charles Townes, who convinced one of the Berkeley faculty to loan Clauser his graduate student, Stuart Freedman, to help. Clauser and Freedman performed the experiments, using a two-photon optical decay of calcium ions and found a violation of the CHSH inequality by 5 standard deviations, publishing their result in 1972 [8].

Alain Aspect’s Non-locality
Just as Clauser’s life was changed when he stumbled on Bell’s obscure paper in 1967, the paper had the same effect on the life of French physicist Alain Aspect who stumbled on it in 1975. Like Clauser, he also sought out Bell for his opinion, meeting with him in Geneva, and Aspect similarly received Bell’s encouragement, this time with the hope to build upon Clauser’s work.

In some respects, the conceptual breakthrough achieved by Clauser had been the CHSH inequality that could be tested experimentally. The subsequent Clauser Freedman experiments were not a conclusion, but were just the beginning, opening the door to deeper tests. For instance, in the Clauser-Freedman experiments, the polarizers were static, and the detectors were not widely separated, which allowed the measurements to be time-like separated in spacetime. Therefore, the fundamental non-local nature of quantum physics had not been tested.
Aspect began a thorough and systematic program, that would take him nearly a decade to complete, to test the CHSH inequality under conditions of non-locality. He began with a much brighter source of photons produced using laser excitation of the calcium ions. This allowed him to perform the experiment in 100’s of seconds instead of the hundreds of hours by Clauser. With such a high data rate, Aspect was able to verify violation of the Bell inequality to 10 standard deviations, published in 1981 [9].
However, the real goal was to change the orientations of the polarizers while the photons were in flight to widely separated detectors [10]. This experiment would allow the detection to be space-like separated in spacetime. The experiments were performed using fast-switching acoustic-optic modulators, and the Bell inequality was violated to 5 standard deviations [11]. This was the most stringent test yet performed and the first to fully demonstrate the non-local nature of quantum physics.
Anton Zeilinger: Master of Entanglement
If there is one physicist today whose work encompasses the broadest range of entangled phenomena, it would be the Austrian physicist, Anton Zeilinger. He began his career in neutron interferometery, but when he was bitten by the entanglement bug in 1976, he switched to quantum photonics because of the superior control that can be exercised using optics over sources and receivers and all the optical manipulations in between.

Working with Daniel Greenberger and Micheal Horne, they took the essential next step past the Bohm two-particle entanglement to consider a 3-particle entangled state that had surprising properties. While the violation of locality by the two-particle entanglement was observed through the statistical properties of many measurements, the new 3-particle entanglement could show violations on single measurements, further strengthening the arguments for quantum non-locality. This new state is called the GHZ state (after Greenberger, Horne and Zeilinger) [12].
As the Zeilinger group in Vienna was working towards experimental demonstrations of the GHZ state, Charles Bennett of IBM proposed the possibility for quantum teleportation, using entanglement as a core quantum information resource [13]. Zeilinger realized that his experimental set-up could perform an experimental demonstration of the effect, and in a rapid re-tooling of the experimental apparatus [14], the Zeilinger group was the first to demonstrate quantum teleportation that satisfied the conditions of the Bennett teleportation proposal [15]. An Italian-UK collaboration also made an early demonstration of a related form of teleportation in a paper that was submitted first, but published after Zeilinger’s, due to delays in review [16]. But teleportation was just one of a widening array of quantum applications for entanglement that was pursued by the Zeilinger group over the succeeding 30 years [17], including entanglement swapping, quantum repeaters, and entanglement-based quantum cryptography. Perhaps most striking, he has worked on projects at astronomical observatories that entangle photons coming from cosmic sources.
By David D. Nolte Nov. 26, 2022
Read more about the history of quantum entanglement in Interference (New From Oxford University Press, 2023)
A popular account of the trials and toils of the scientists and engineers who tamed light and used it to probe the universe.

Video Lectures
Physics Colloquium on the Backstory of the 2023 Nobel Prize in Physics
Timeline
1935 – Einstein EPR
1935 – Bohr EPR
1935 – Schrödinger: Entanglement and Cat
1950 – Madam Wu positron decay
1952 – David Bohm and Non-local hidden variables
1957 – Bohm and Ahronov version of EPR
1963 – Bell’s inequalities
1967 – Clauser reads Bell’s paper
1967 – Commins experiment with Calcium
1969 – CHSH inequality: measurable with detection inefficiencies
1972 – Clauser and Freedman experiment
1975 – Aspect reads Bell’s paper
1976 – Zeilinger reads Bell’s paper
1981 – Aspect two-photon generation source
1982 – Aspect time variable analyzers
1988 – Parametric down-conversion of EPR pairs (Shih and Alley, Ou and Mandel)
1989 – GHZ state proposed
1993 – Bennett quantum teleportation proposal
1995 – High-intensity down-conversion source of EPR pairs (Kwiat and Zeilinger)
1997 – Zeilinger quantum teleportation experiment
1999 – Observation of the GHZ state
Bibliography
[1] See the full details in: David D. Nolte, Interference: A History of Interferometry and the Scientists Who Tamed Light (Oxford University Press, July 2023)
[2] A. Einstein, B. Podolsky, N. Rosen, Can quantum-mechanical description of physical reality be considered complete? Physical Review 47, 0777-0780 (1935).
[3] N. Bohr, Can quantum-mechanical description of physical reality be considered complete? Physical Review 48, 696-702 (1935).
[4] E. Schrödinger, Die gegenwärtige Situation in der Quantenmechanik. Die Naturwissenschaften 23, 807-12; 823-28; 844-49 (1935).
[5] D. Bohm, A suggested interpretation of the quantum theory in terms of hidden variables .1. Physical Review 85, 166-179 (1952); D. Bohm, A suggested interpretation of the quantum theory in terms of hidden variables .2. Physical Review 85, 180-193 (1952).
[6] J. Bell, On the Einstein-Podolsky-Rosen paradox. Physics 1, 195 (1964).
[7] 1. J. F. Clauser, M. A. Horne, A. Shimony, R. A. Holt, Proposed experiment to test local hidden-variable theories. Physical Review Letters 23, 880-& (1969).
[8] S. J. Freedman, J. F. Clauser, Experimental test of local hidden-variable theories. Physical Review Letters 28, 938-& (1972).
[9] A. Aspect, P. Grangier, G. Roger, EXPERIMENTAL TESTS OF REALISTIC LOCAL THEORIES VIA BELLS THEOREM. Physical Review Letters 47, 460-463 (1981).
[10] Alain Aspect, Bell’s Theorem: The Naïve Veiw of an Experimentalit. (2004), hal- 00001079
[11] A. Aspect, J. Dalibard, G. Roger, EXPERIMENTAL TEST OF BELL INEQUALITIES USING TIME-VARYING ANALYZERS. Physical Review Letters 49, 1804-1807 (1982).
[12] D. M. Greenberger, M. A. Horne, A. Zeilinger, in 1988 Fall Workshop on Bells Theorem, Quantum Theory and Conceptions of the Universe. (George Mason Univ, Fairfax, Va, 1988), vol. 37, pp. 69-72.
[13] C. H. Bennett, G. Brassard, C. Crepeau, R. Jozsa, A. Peres, W. K. Wootters, Teleporting an unknown quantum state via dual classical and einstein-podolsky-rosen channels. Physical Review Letters 70, 1895-1899 (1993).
[14] J. Gea-Banacloche, Optical realizations of quantum teleportation, in Progress in Optics, Vol 46, E. Wolf, Ed. (2004), vol. 46, pp. 311-353.
[15] D. Bouwmeester, J.-W. Pan, K. Mattle, M. Eibl, H. Weinfurter, A. Zeilinger, Experimental quantum teleportation. Nature 390, 575-579 (1997).
[16] D. Boschi, S. Branca, F. De Martini, L. Hardy, S. Popescu, Experimental realization of teleporting an unknown pure quantum state via dual classical and Einstein-podolsky-Rosen Channels. Phys. Rev. Lett. 80, 1121-1125 (1998).
[17] A. Zeilinger, Light for the quantum. Entangled photons and their applications: a very personal perspective. Physica Scripta 92, 1-33 (2017).