Somewhere, within the craft of conformal maps, lie the answers to dark, difficult problems of physics.

For instance, can you map out the electric field lines around one of Benjamin Franklin’s pointed lightning rods?

Can you calculate the fluid velocities in a channel making a sharp right angle?

Now take it up a notch in difficulty: Can you find the distribution of the sizes of magnetic domains within a flat magnet that is about to depolarize?

Or take it to the max: Can you find the vibration frequencies of the cosmic strings of string theory?

The answers to all these questions starts with simple physics solutions within simple boundaries—sometimes a problem so simple even a freshman physics student can solve it—and then mapping the solution, point by point, onto the geometry of the desired problem.

Once the right mapping function is found, you can solve some of the stickiest, ugliest, crankiest problems of physics like a pro.

The Earliest Conformal Maps

What is a conformal map?  It is a transformation that takes one picture into another, keeping all local angles unchanged, no matter how distorted the overall transformation is.

This property was understood by the very first mathematicians, wrangling their sexagesimal numbers by the waters of Babylon as they mapped the heavens onto charts to foretell the coming of the seasons.

Hipparchus of Rhodes, around 150 BCE during the Hellenistic transition from Alexander to Caesar, was the first to describe the stereographic projection by which the locations of the stars were mapped on a plane by locating all the stars on the celestial sphere and tracing a line from the bottom of the sphere to the star and plotting where the line intersects the mid plane.  Why this method should be conformal, preserving the angles, was probably beyond his mathematical powers, but he probably intuitively knew that it did.

Ptolemy of Alexandria around 150 CE, expanded on Hipparchus’ star charts and then introduced his own conical-like projection to map all the known world of his day.  The Ptolemaic projection is almost conformal, but not quite.  He was more interested in keeping areas faithful than angles.

Mercator’s Rules of Rhumb

The first conformal mapping of the Earth’s surface onto the plane was constructed by Gerard Mercator in 1569.  His goal, as a map maker, was to construct a map that traced out a ship’s course of constant magnetic bearing as a straight line, known as a rhumb line.  This mapping property had important utility for navigators, especially on long voyages at sea beyond the sight of land, and was a hallmark of navigation maps of the Mediterranean, known as Portolan Charts.  Rhumb lines were easy to draw on the small scales of the middle ocean, but on the scale of the Earth, no one knew how to do it.

Though Mercator’s life and career have been put under the biographer’s microscope numerous times, the exact moment when he realized how to make his map—the now-famous Mercator Projection—is not known.  It is possible that he struck a compromise between a cylindrical point projection, that stretched the arctic regions, and a cylindrical line projection that compressed the arctic regions.  He also was a maker of large globes on which rhumb lines (actually curves) could be measured and transferred to a flat map.  Either way, he knew that he had invented something entirely new, and he promoted his map as an aid for the Age of Exploration.  There is some evidence that Frobisher took Mercator’s map with him during his three famous arctic expeditions seeking the Northwest Passage.

Mercator never explained nor described the mathematical function behind his projection.  This was first discovered by the English mathematician Thomas Harriot in 1589, 20 years after Mercator published his map, as Harriot was helping Sir Walter Rayleigh with his New World projects.  Like most of what Harriot did during his lifetime, he was years (sometimes decades) ahead of anyone else, but no one ever knew because he never published.  His genius remained buried in his personal notes until they were uncovered in the late 1800’s long after others had claimed credit for things he did first.

The rhumb lines of Mercator’s map maintain constant angle relative to all lines of longitude and hence the Mercator projection is a conformal map.  The mathematical proof of this fact was first given by James Gregory in 1668 (almost a century after Mercator’s feat) followed by a clearer proof by Isaac Barrow in 1670.  It was 25 years later that Edmund Halley (of Halley’s Comet fame) proved that the stereographic projection was also conformal.

A hundred years passed after Halley before anyone again looked into the conformal properties of mapping—and then the field exploded.

The Rube in Frederick’s Berlin

In 1761, the Swiss contingent of the Prussian Academy of Sciences nominated a little-known self-taught Swiss mathematician to the membership of the Academy.  The process was pro forma, but everyone nominated was interviewed personally by Frederick the Great who had restructured the Academy years before from a backwater society to a leading scientific society in Europe.  When Frederick met Johann Lambert, he thought it must be a practical joke.  Lambert looked strange, dressed strangely, and his manners were even stranger.  He was born poor, had never gone to school, and he looked it and he talked it. 

Frederick rejected the nomination.

But the Swiss contingent, led by Leonhard Euler himself, persisted, because they knew what Frederick did not—Lambert was a genius.  He was an autodidact who had pulled himself up so thoroughly, that he had self-published some of the greatest works of philosophy and science of his generation.  One of these was on the science of optics which established standards of luminance that we still use today.  (In my own laboratory, my students and I routinely refer to Lambertian surfaces in our research on laser speckle.  And we use the Lambert-Beer law of optical attenuation every day in our experiments.)

Frederick finally relented after a delay of two years, and admitted Lambert to his Academy, where Lambert went on a writing rampage, publishing a paper a month over the next ten years, like a dam letting loose.

One of Lambert’s many papers was on projection maps of the Earth.  He not only picked up where Halley had left off a hundred years earlier, but he invented 7 new projections, three of which were conformal and four of which were equal area.  Three of Lambert’s projections are in standard use today in cartography. 

Although Lambert worked at the time of Euler, Euler’s advances in complex-valued mathematics was still young and not well known, so Lambert worked his projections using conventional calculus.  It would be another 100 years before the power of complex analysis was brought fully to bear on the problem of conformal mappings.

Riemann’s Sphere

It seems like the history of geometry can be divided into two periods: the time before Bernhard Riemann and the time after Bernhard Riemann. 

Bernhard Riemann was a gentle giant, a shy and unimposing figure with a Herculean mind.  He transformed how everyone thought about geometry, both real and complex.  His doctoral thesis was the most complete exposition to date on the power of complex analysis, and his Habilitation Lecture on the foundations of geometry shook those very foundations to their core.

In the hands of Riemann, the stereographic projection became a complex transform of the simplest type

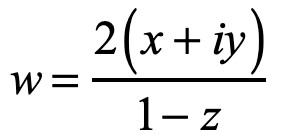
where x, y and z are the spherical coordinates of a point on the sphere.

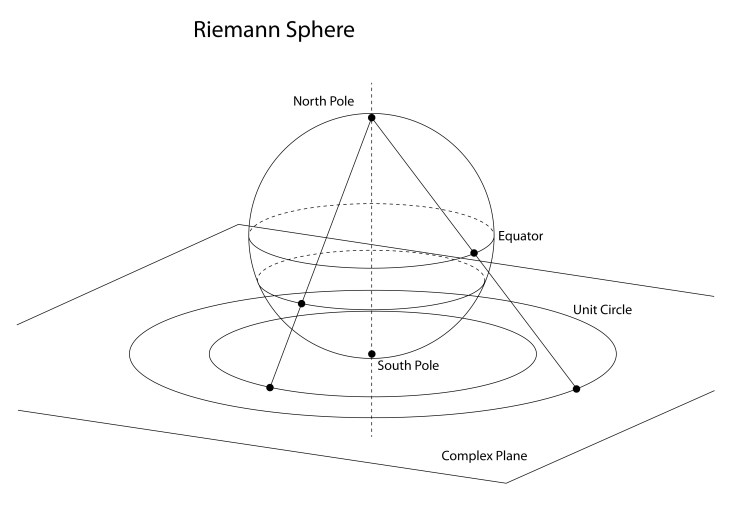
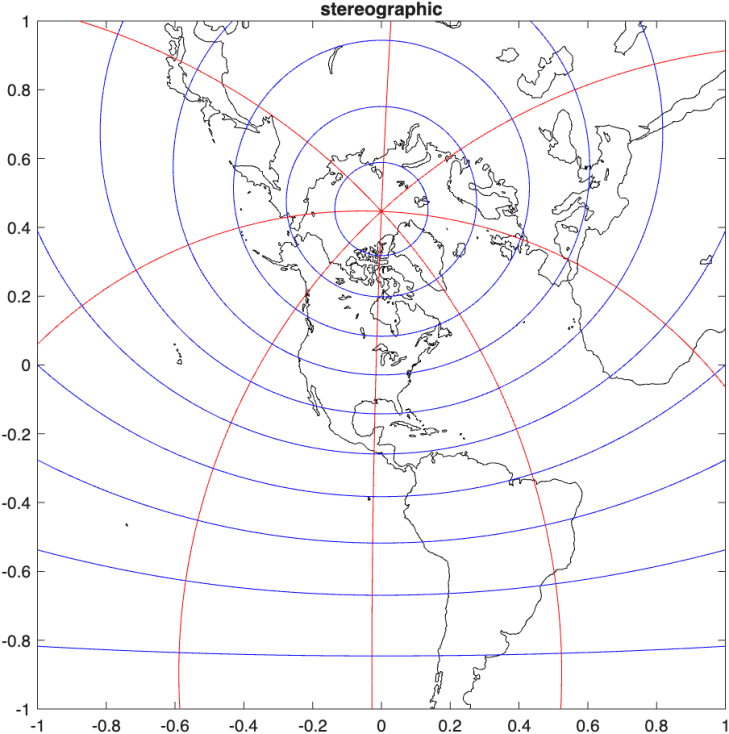
The projection in Fig. 9 is from the North Pole, which represents Antarctica faithfully but distorts the lands of the Northern Hemisphere. Any projection can be centered on a chosen point of the Earth by projecting from the opposite point, called the antipode. For instance, the stereographic projection centered on Chicago is shown in Fig. 10.

Building on the work of Euler and Cauchy, Riemann dove into conformal maps and emerged in 1851 with one of the most powerful theorems in complex analysis, known as the Riemann Mapping Theorem:

Any non-empty, simply connected open subset of the complex plane (which is not the entire plane itself) can be conformally mapped to the open unit disk. 

An immediate consequence of this is that all non-empty, simply connected open subsets of the complex plane are equivalent, because any domain can be mapped onto the unit disk, and then the unit disk can be mapped to any domain.

The consequences of this are astounding:  Solve a simple physics problem in a simple domain and then use the Riemann mapping theorem to transform it into the most complex, ugly, convoluted, twisted problem you can think of (as long as it is simply connected) and then you have the answer.

The reason that conformal maps (that are purely mathematical) allow the transformation of physics problems (that are “real”) is because physics is based on orthogonal sets of fields and potentials that govern how physical systems behave.  In other words, the solution to the Laplacian operator on one domain can be transformed to a solution of the Laplacian operator on a different domain.

Powerful! Great!  But how do you do it?  Riemann’s theorem was an existence proof—not a solution manual.  The mapping transformations still needed to be found.

Schwarz-Christoffel

On the heels of Bernard Riemann, who had altered the course of geometry, Hermann Schwarz at the University of Halle, Germany, and Elwin Bruno Christoffel at the Technical University in Zürich, Switzerland, took up Riemann’s mapping theorem to search for the actual mappings that would turn the theorem from “nice to know” to an actual formula.

Working independently, Christoffel in 1867 drew on his expertise in differential geometry while Schwarz in 1869 drew on his expertise in the calculus of variations, both with a solid background in geometry and complex analysis.  They focused on conformal maps of polygons because general domains on the complex plane can be described with polygonal boundaries.  The conformal map they sought would take simple portions of the complex plane and map them to the interior angle of a polygonal vertex.  With sufficient constraints, the goal was to map all the vertexes and hence the entire domain.

The surprisingly simple result is known as the Schwarz-Christoffel equation

where a, b, c … are the positions of the vertices, and α, β, γ … are the interior angles of the vertices.  The integral needs to be carried out on the complex plane, but it has closed-form solutions for many common cases.

This equation solves the problem of “how” that allows any physics solution on one domain to be mapped to another domain.

Conformal Maps

The list of possible conformal maps is literally limitless, yet there are a few that are so common that they deserve to be explored in some detail here.

One conformal map is so “famous” it has the name of the Joukowski Map that takes the upper half plane and transforms it (through an open strip) onto the full complex plane. The field lines and potentials are shown in Fig. 11 as a simple transform of straight lines. To calculate these fields and potentials directly would require the solution of a partial differential equation (PDE) through numerical methods.

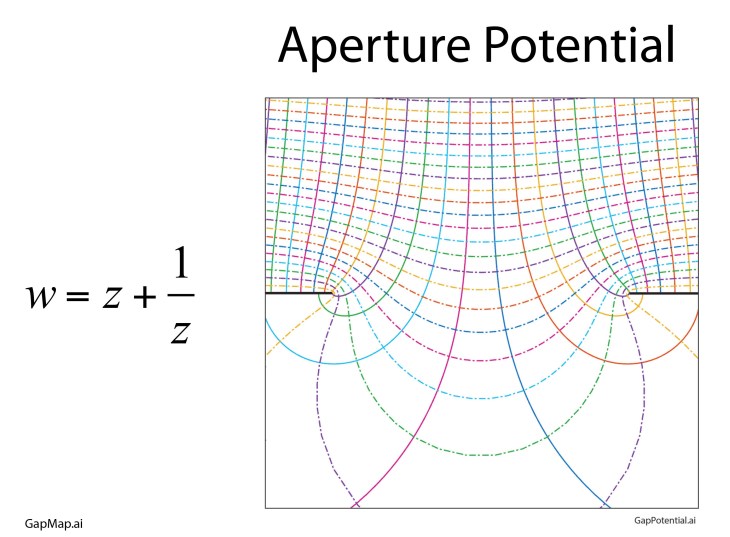
Other common conformal maps are power-law transformations, taking the upper half plane into the full plane. Fig. 12 shows three of these, the first an inner half corner, the second the outer half corner, and the third transforming the upper half plane onto the full plane. All three of these show the field lines and the potentials near charged conducting plates.

Conformal maps can also be “daisy-chained”. For instance, in Fig. 13, the unit circle is transformed into the upper half plane, providing the field lines and equipotentials of a point charge near a conducting plate. The fields are those of a point charge and its image charge, creating a dipole potential. This charge and its image are transformed again into the fields and potentials of a point charge near a conducting corner.

But we are not quite done with conformal maps. They have reappeared in recent years in exciting new areas of physics in the form of conformal field theory.

Conformal Field Theory

The importance being conformal extends far beyond solutions to Laplace’s equation.  Physics is physics, regardless of how it comes about and how it is described, and transformations cannot change the physics.  As an example, when a many-body system is at a critical point, then the description of the system is scale independent.  In this case, changing scale is one type of transformation that keeps the physics the same.  Conformal maps also keep the physics the same by preserving angles.  Taking this idea into the quantum realm, a quantum field theory of a scale-invariant system can be conformally mapped onto other, more complex systems for which answers are not readily derived. 

This is why conformal field theory (CFT) has become an important new field of physics with applications ranging as widely as quantum phase transitions and quantum strings.

---