Ask any school child which scientist first dropped balls from a leaning tower to measure how fast they fell, and you will receive the confident answer: Galileo. But they would be wrong!
Ask any musician who was the first to propose a well-tempered musical instrument, and many will say: Johann Sebastian Bach. And they would be wrong!
Ask any mathematician who invented the decimal notation, and almost all will answer: John Napier. And they would be almost right, but not quite!
Ask anyone how the dime got its name, and no one can say. Because almost no one knows.
But there is one person behind all the answers: Simon Stevin of Bruges!
The Renaissance Man
Simon Stevin was born in Bruges, the Flemish capital of the Low Countries, in 1548, five years after Copernicus published his heliocentric model of the universe, and he lived just long enough to see Kepler lay down his laws in Epitome astronomiae Copernicanae, published in 1619. This was the dawn of the Scientific Revolution, where Copernicus and Galileo and Kepler take center stage. Stevin was right there with them, and he was just as influential in his own time, but his star faded after his death, eclipsed by better press—Galileo, after all, was a master at it. Yet the echoes of Stevin’s discoveries reverberate today. Every time you write a decimal fraction, every time you sit down at a tuned piano, every time you reach for a dime, you are receiving the legacy of Simon Stevin.
Stevin was born a nobody, an illegitimate son who fortunately was acknowledged and educated by his family. He left Bruges in 1571 to escape the Spanish reign of terror against protestants, traveling across the continent to learn about the wider world and how it worked. In the convoluted politics of the sixteenth century, Catholic Spain had been given dominion over the mostly Protestant Netherlands and conflict was the rule, but in 1579 the seven northern provinces united, led by William of Orange, breaking free from Spain in 1581. Stevin was drawn back to the Low Countries and to the new republic, enrolling as a student at the University of Leiden where he became close friends with William of Orange’s second son, Maurits, Prince of Orange. Maurits was heir to William because his older brother was loyal to Spain. When William was assassinated in 1584 in Delft, Maurits assumed command of his father’s army in the war against Spain and he asked Stevin to serve as a military advisor. Stevin left the university, never returning to receive a degree, and for the next 20 years helped Prince Maurits expel the Spanish from the United Provinces.
Where and when Stevin had time to educate himself is anyone’s guess, but by the time of the truce of 1609, he had published 8 books that ranged in topics from book-keeping to hydraulics to weights-and-measures to compounded interest to political science to mathematics and more. Most of these were written in Dutch instead of Latin, making them accessible to the rising artesan class, and many were translated into other languages (by Willebord Snellius of “Snell’s Law” fame), where their practical impact on commerce and trade and daily life outweighed the more ethereal works of his better known contemporaries Galileo and Kepler.

Because the Netherlands were a seafaring country focused on trade, the physics of hydraulics as well as the physics of weights and measures were of direct usefulness, and Stevin’s always pragmatic interests were drawn to problems of buoyancy and stability, making him one of the Renaissance’s first physicists.
The Law of Fall
In all the contemporary documents associated with the life of Galileo, there is no evidence that he ever dropped balls from the leaning tower of Pisa. The story first appears in a biography of Galileo by the student of a student—by Vincenzo Viviani who was a pupil of Torricelli, writing about events that took place half a century earlier. The story goes that Galileo, while in Pisa in 1589, dropped weights of the same material but different masses from the leaning tower and showed that they fell at the same rates, demonstrating a clear departure from the physics of Aristotle who would have claimed that the heavier weight fell faster.
It is easy to see how a leaning tower might help in such an experiment, allowing the balls to be dropped carefully from rest and to fall vertically while clearing the base of the building. Coincidentally, there is another famous leaning tower in Europe, the Oude Kerk in Delft, in the Netherlands, built in 1350 at the edge of the old canal known as Oude Delft. The soft earth at the edge of the canal sagged as the church tower was being built, and though the builders tilted each new section to be vertical, to this day the church tower leans ominously.

Despite the lack of evidence that Galileo ever performed the experiment, there is solid evidence that Stevin did the experiment himself by 1586 (three years before Galileo) when he published his book on buoyancy and statics. Enlisting the help of the burgomaster of Delft, Jan de Groot, two weights of the same size, but differing in mass by about a factor of ten, were dropped from 30 feet up onto a wooden board. The time of fall was evaluated differentially by the sounds of the impacts on the board, which were nearly simultaneous, despite the large difference in mass, clearly refuting Aristotle’s physics.
Although Stevin gives many specific details of the experiment, he does not say exactly where it was performed. It has often been assumed that the experiment was performed at the Neue Kerk in the main square of Delft, since this was the tallest building in Delft at that time. But my money is on the Oude Kerk with its convenient tilt. I am not aware of anyone else making this connection. I have seen the Oude Kerk myself and its constant-width tower is perfect for dropping weights. And 30 feet is not that high, so there was no need to perform the experiment at the much taller Neue Kerk.
It is possible that the leaning tower of Pisa was substituted for the leaning tower of Delft in Viviani’s hagiography of Galileo, or that Galileo, knowing of Stevin’s experiment, described what would have happened had he repeated it. Biographies by disciples are never reliable, while Stevin’s writings are known for their even handedness. Furthermore, Stevin published before Galileo is supposed to have done his experiment, so Stevin had nothing to prove to anyone in his writing. There was no priority dispute.
None of this takes away from what Galileo accomplished. His experiments performed with balls on inclined planes were exquisitely detailed, complete and accurate—the forerunners of the kind of careful experimental study that elicit new laws of physics. Furthermore, Galileo’s thorough mathematical analysis of his experimental results inaugurated the field of mathematical physics. Stevin’s priority for dropping balls from leaning towers cannot place him ahead of Galileo for the epic shifting of paradigms.
Although Stevin had no personal connection to Galileo in the realm of physics, he did have a connection in the realm of music theory, not to Galileo himself, but to Galileo’s father.
Musical Temperament
Why do a pair of notes on a perfect fifth sound so harmonious? Why do other pairs sound dissonant? These questions are at the root of music theory that have perplexed mathematicians and physicists since the days of Pythagoras. Pythagoras proposed the ratio of small integers as the explanation, which works fine for the most fundamental intervals on the octave.
An octave consists of 8 notes with seven half-tone intervals. One octave is a factor of 2 in frequency. If the frequency of a root note is f0, then the note one octave higher is 2•f0. In Western music, the diatonic scale is the most common to span an octave. It contains 7 notes plus the octave (to make 8), such as C-D-E-F-G-A-B-C for the scale of C-major. In this diatonic scale the fifth note G is the most important. Pythagoras established that the ratio of the fifth to the root goes as the ratio of 3:2, or as we would say today, a frequecy of 1.5•f0. Furthermore, successive fifths define the root diatonic, such as C-G-D-A-E-B-F-C that spans 7 fifths and 4 octaves bringing the frequency to 16•f0.
But here is the problem that vexed musical theorists for over a millennium:
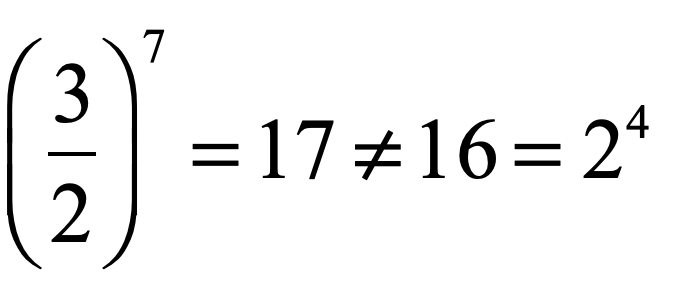
It doesn’t work! The ratio of 3:2 applied 7 times gives a frequency of 17•f0, but it should only be a frequency of 16•f0 for four octaves in frequency. There is an error of 6%! What happened?

During the early Renaissance, lutes had evolved to have as many as 14 strings that the lutenist had to tune, and the best musicians, those with perfect pitch, knew that when tuning a lute in the scale of D, the tone of the “C” note was slightly different than if the lute were tuned in the scale of C. In other words, every key required slightly different frequencies even for the same “note”.
Yet there were some lutenists who realized that the differences were so minor, that a “compromise” tuning, known as a temperament, could be found so that songs in different keys would not require an entire retuning of all 14 strings.
Enter Galileo’s father, Vincenzo Galilei, a minor aristocrat without means who partially supported himself as a lutenist. He had studied music under Gioseffo Zarlino in Venice, who had used an approach developed by Ptolemy that extended the Pythagorean ratios of the numbers 2, 3 and 4 to include the numbers 5 and 6 relying on superparticular ratios (in which the numerator is one unit more than the denominator) of 3/2, and 4/3 that were extended to include 5/4 and 6/5 as the basis of consonance. Later, Vincenzo came to realize that tuning on these ratios prevented continuous modulation across scales, so he settled on a superparticular ratio of 18/17 = 1.0588 as the multiplier that increased the frequency on a half-note interval, allowing a player to transition smoothly among scales without retuning. He published his modern theory of music intonation in a book in 1581 (the same year that his son began attending classes at the University in Pisa). [1]
Vincenzo Galilei’s solution was very close, but it was still in the Pythagorean vein. Stevin realized there was a better approach. By using Vincenzo’s ratio, multiplying it by itself 12 times while increasing one octave by taking 12 steps, the frequency of the higher tonic would be
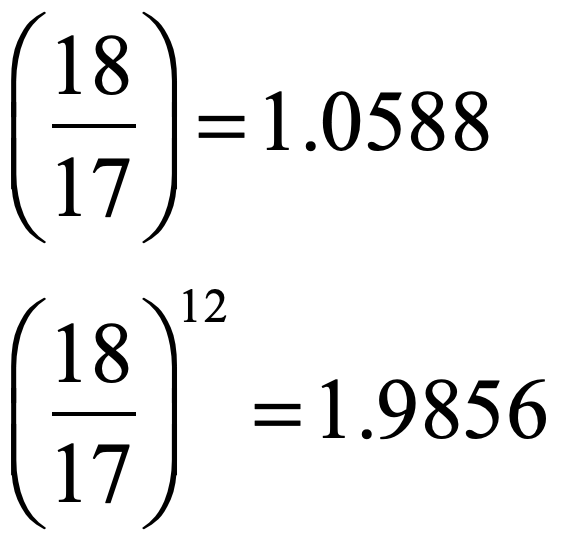
which is within 1% of the perfect factor of 2. But a perfect factor of 2 is what is required by a perfect theory of musical tone. Therefore, Stevin reasoned that the true factor, when multiplied by itself 12 times should yield a perfect factor of 2. The obvious answer is
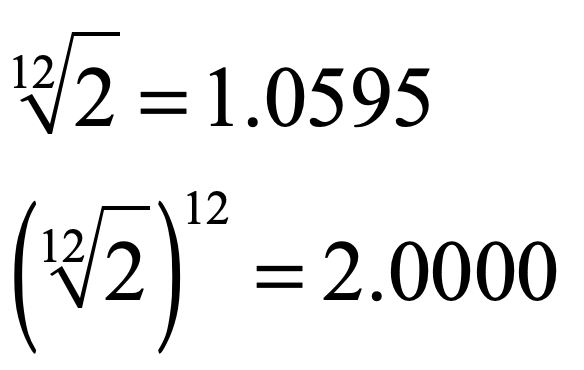
At the turn of the seventeenth century, algebraic methods for calculating roots were already established, and Stevin wrote up his idea in the manuscript De Spiegheling der Singconst (Theory of the Art of Singing, ca. 1605). Though he was a persistent publisher, this one never quite got into print, remaining in manuscript form until 1884, well after issues of temperament had been established. But it established a rational mathematical approach (based on an irrational number) that differed from the Pythagorean reliance on ratios of integers.
Decimal Notation
In Stevin’s day, not only music, but numbers too were being held hostage by Pythagoras’ legacy. Measurements were made as fractions: 1/2, 1/4, 1/3, 1/16, etc. (In the US we are still held hostage by this ancient method when we talk of a “sixteenth” or a “thirtysecond” of an inch.)
Stevin thought of a more rational approach that would facilitate computations of addition, subtraction, multiplication and division. All fraction can be expressed as sums of powers with variable coefficients. For instance

But this example is in “octal” just to illustrate the point. What Stevin recognized is that the approach can be used with Fibonacci’s Indo-Arabic numerals based on 10 digits. Then
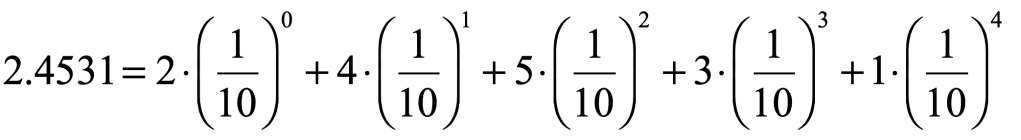
Stevin, inventing a new notation, expressed this as
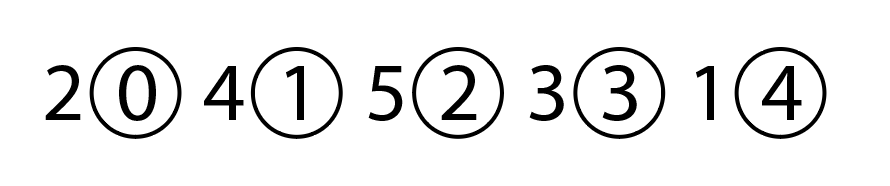
where he explicitly writes out the successive powers. This notation was later shortened to include only the symbol for the zeroth power, since the place notation implicitly included the other powers. The zeroth-power symbol became a point in some versions and a comma in other versions in wide-spread use today.
Stevin’s booklet on decimal notation was called De Thiende (The Art of Tenths) and was translated into French as Le Disme (pronounced “dime”, where the s is silent). Thomas Jefferson was directly influenced by the idea of decimal coinage when he was deciding on the currency system for the new United States of America. He was looking for a more rational approach than the old British usage of shillings and pennies and farthings (or the “pieces of eight” in the southern maritimes) that had no obvious relationship to each other for anyone not used to their system. So Jefferson adopted one hundred cents to the dollar and the “dime” for the ten-cent coin, paying homage to Simon Stevin of Bruges.

References
[1] D. D. Nolte, Galileo Unbound: A Path Across Life, the Universe and Everything (Oxford University Press, 2018). (Read about the personal dramas of scientists and mathematicians as they developed the physics of motion.)

