Arthur Eddington was the complete package—an observationalist with the mathematical and theoretical skills to understand Einstein’s general theory, and the ability to construct the theory of the internal structure of stars. He was Zeus in Olympus among astrophysicists. He always had the last word, and he stood with Einstein firmly opposed to the Schwarzschild singularity. In 1924 he published a theoretical paper in which he derived a new coordinate frame (now known as Eddington-Finkelstein coordinates) in which the singularity at the Schwarzschild radius is removed. At the time, he took this to mean that the singularity did not exist and that gravitational cut off was not possible [1]. It would seem that the possibility of dark stars (black holes) had been put to rest. Both Eddington and Einstein said so! But just as they were writing the obituary of black holes, a strange new form of matter was emerging from astronomical observations that would challenge the views of these giants.
Something wonderful, but also a little scary, happened when Chandrasekhar included the relativistic effects in his calculation.
White Dwarf
Binary star systems have always held a certain fascination for astronomers. If your field of study is the (mostly) immutable stars, then the stars that do move provide some excitement. The attraction of binaries is the same thing that makes them important astrophysically—they are dynamic. While many double stars are observed in the night sky (a few had been noted by Galileo), some of these are just coincidental alignments of near and far stars. However, William Herschel began cataloging binary stars in 1779 and became convinced in 1802 that at least some of them must be gravitationally bound to each other. He carefully measured the positions of binary stars over many years and confirmed that these stars showed relative changes in position, proving that they were gravitational bound binary star systems [2]. The first orbit of a binary star was computed in 1827 by Félix Savary for the orbit of Xi Ursae Majoris. Finding the orbit of a binary star system provides a treasure trove of useful information about the pair of stars. Not only can the masses of the stars be determined, but their radii and densities also can be estimated. Furthermore, by combining this information with the distance to the binaries, it was possible to develop a relationship between mass and luminosity for all stars, even single stars. Therefore, binaries became a form of measuring stick for crucial stellar properties.

One of the binary star systems that Hershel discovered was the pair known as 40 Eridani B/C, which he observed on January 31 in 1783. Of this pair, 40 Eridani B was very dim compared to its companion. More than a century later, in 1910 when spectrographs were first being used routinely on large telescopes, the spectrum of 40 Eridani B was found to be of an unusual white spectral class. In the same year, the low luminosity companion of Sirius, known as Sirius B, which shared the same unusual white spectral class, was evaluated in terms of its size and mass and was found to be exceptionally small and dense [3]. In fact, it was too small and too dense to be believed at first, because the densities were beyond any known or even conceivable matter. The mass of Sirius B is around the mass of the Sun, but its radius is comparable to the radius of the Earth, making the density of the white star about ten thousand times denser than the core of the Sun. Eddington at first felt the same way about white dwarfs that he felt about black holes, but he was eventually swayed by the astrophysical evidence. By 1922 many of these small white stars had been discovered, called white dwarfs, and their incredibly large densities had been firmly established. In his famous book on stellar structure [4], he noted the strange paradox: As a star cools, its pressure must decrease, as all gases must do as they cool, and the star would shrink, yet the pressure required to balance the force of gravity to stabilize the star against continued shrinkage must increase as the star gets smaller. How can pressure decrease and yet increase at the same time? In 1926, on the eve of the birth of quantum mechanics, Eddington could conceive of no mechanism that could resolve this paradox. So he noted it as an open problem in his book and sent it to press.
Subrahmanyan Chandrasekhar
Three years after the publication of Eddington’s book, an eager and excited nineteen-year-old graduate of the University in Madras India boarded a steamer bound for England. Subrahmanyan Chandrasekhar (1910—1995) had been accepted for graduate studies at Cambridge University. The voyage in 1930 took eighteen days via the Suez Canal, and he needed something to do to pass the time. He had with him Eddington’s book, which he carried like a bible, and he also had a copy of a breakthrough article written by R. H. Fowler that applied the new theory of quantum mechanics to the problem of dense matter composed of ions and electrons [5]. Fowler showed how the Pauli exclusion principle for electrons, that obeyed Fermi-Dirac statistics, created an energetic sea of electrons in their lowest energy state, called electron degeneracy. This degeneracy was a fundamental quantum property of matter, and carried with it an intrinsic pressure unrelated to thermal properties. Chandrasekhar realized that this was a pressure mechanism that could balance the force of gravity in a cooling star and might resolve Eddington’s paradox of the white dwarfs. As the steamer moved ever closer to England, Chandrasekhar derived the new balance between gravitational pressure and electron degeneracy pressure and found the radius of the white dwarf as a function of its mass. The critical step in Chandrasekhar’s theory, conceived alone on the steamer at sea with access to just a handful of books and papers, was the inclusion of special relativity with the quantum physics. This was necessary, because the densities were so high and the electrons were so energetic, that they attained speeds approaching the speed of light.
Something wonderful, but also a little scary, happened when Chandrasekhar included the relativistic effects in his calculation. He discovered that electron degeneracy pressure could balance the force of gravity if the mass of the white dwarf were smaller than about 1.4 times the mass of the Sun. But if the dwarf was more massive than this, then even the electron degeneracy pressure would be insufficient to fight gravity, and the star would continue to collapse. To what? Schwarzschild’s singularity was one possibility. Chandrasekhar wrote up two papers on his calculations, and when he arrived in England, he showed them to Fowler, who was to be his advisor at Cambridge. Fowler was genuinely enthusiastic about the first paper, on the derivation of the relativistic electron degeneracy pressure, and it was submitted for publication. The second paper, on the maximum sustainable mass for a white dwarf, which reared the ugly head of Schwarzschild’s singularity, made Fowler uncomfortable, and he sat on the paper, unwilling to give his approval for publication in the leading British astrophysical journal. Chandrasekhar grew annoyed, and in frustration sent it, without Fowler’s approval, to an American journal, where “The Maximum Mass of Ideal White Dwarfs” was published in 1931 [6]. This paper, written in eighteen days on a steamer at sea, established what became known as the Chandrasekhar limit, for which Chandrasekhar would win the 1983 Nobel Prize in Physics, but not before he was forced to fight major battles for its acceptance.

Chandrasekhar versus Eddington
Initially there was almost no response to Chandrasekhar’s paper. Frankly, few astronomers had the theoretical training needed to understand the physics. Eddington was one exception, which was why he held such stature in the community. The big question therefore was: Was Chandrasekhar’s theory correct? During the three years to obtain his PhD, Chandrasekhar met frequently with Eddington, who was also at Cambridge, and with colleagues outside the university, and they all encouraged Chandrasekhar to tackle the more difficult problem to combine internal stellar structure with his theory. This could not be done with pen and paper, but required numerical calculation. Eddington was in possession of an early electromagnetic calculator, and he loaned it to Chandrasekhar to do the calculations. After many months of tedious work, Chandrasekhar was finally ready to confirm his theory at the 1934 meeting of the British Astrophysical Society.
The young Chandrasekhar stood up and gave his results in an impeccable presentation before an auditorium crowded with his peers. But as he left the stage, he was shocked when Eddington himself rose to give the next presentation. Eddington proceeded to criticize and reject Chandrasekhar’s careful work, proposing instead a garbled mash-up of quantum theory and relativity that would eliminate Chandrasekhar’s limit and hence prevent collapse to the Schwarzschild singularity. Chandrasekhar sat mortified in the audience. After the session, many of his friends and colleagues came up to him to give their condolences—if Eddington, the leader of the field and one of the few astronomers who understood Einstein’s theories, said that Chandrasekhar was wrong, then that was that. Badly wounded, Chandrasekhar was faced with a dire choice. Should he fight against the reputation of Eddington, fight for the truth of his theory? But he was at the beginning of his career and could ill afford to pit himself against the giant. So he turned his back on the problem of stellar death, and applied his talents to the problem of stellar evolution.
Chandrasekhar went on to have an illustrious career, spent mostly at the University of Chicago (far from Cambridge), and he did eventually return to his limit as it became clear that Eddington was wrong. In fact, many at the time already suspected Eddington was wrong and were seeking for the answer to the next question: If white dwarfs cannot support themselves under gravity and must collapse, what do they collapse to? In Pasadena at the California Institute of Technology, an astrophysicist named Fritz Zwicky thought he knew the answer.
Fritz Zwicky’s Neutron Star
Fritz Zwicky (1898—1874) was an irritating and badly flawed genius. What made him so irritating was that he knew he was a genius and never let anyone forget it. What made him badly flawed was that he never cared much for weight of evidence. It was the ideas that mattered—let lesser minds do the tedious work of filling in the cracks. And what made him a genius was that he was often right! Zwicky pushed the envelope—he loved extremes. The more extreme a theory was, the more likely he was to favor it—like his proposal for dark matter. Most of his colleagues considered him to be a buffoon and borderline crackpot. He was tolerated by no one—no one except his steadfast collaborator of many years Ernst Baade (until they nearly came to blows on the eve of World War II). Baade was a German physicist trained at Göttingen and recently arrived at Cal Tech. He was exceptionally well informed on the latest advances in a broad range of fields. Where Zwicky made intuitive leaps, often unsupported by evidence, Baade would provide the context. Baade was a walking Wikipedia for Zwicky, and together they changed the face of astrophysics.
Zwicky and Baade submitted an abstract to the American Physical Society Meeting in 1933, which Kip Thorne has called “…one of the most prescient documents in the history of physics and astronomy” [7]. In the abstract, Zwicky and Baade introduced, for the first time, the existence of supernovae as a separate class of nova and estimated the total energy output of these cataclysmic events, including the possibility that they are the source of some cosmic rays. They introduced the idea of a neutron star, a star composed purely of neutrons, only a year after Chadwick discovered the neutron’s existence, and they strongly suggested that a supernova is produced by the transformation of a star into a neutron star. A neutron star would have a mass similar to that of the Sun, but would have a radius of only tens of kilometers. If the mass density of white dwarfs was hard to swallow, the density of a neutron star was billion times greater! It would take nearly thirty years before each of the assertions made in this short abstract were proven true, but Zwicky certainly had a clear view, tempered by Baade, of where the field of astrophysics was headed. But no one listened to Zwicky. He was too aggressive and backed up his wild assertions with too little substance. Therefore, neutron stars simmered on the back burner until more substantial physicists could address their properties more seriously.
Two substantial physicists who had the talent and skills that Zwicky lacked were Lev Landau in Moscow and Robert Oppenheimer at Berkeley. Landau derived the properties of a neutron star in 1937 and published the results to great fanfare. He was not aware of Zwicky’s work, and he called them neutron cores, because he hypothesized that they might reside at the core of ordinary stars like the Sun. Oppenheimer, working with a Canadian graduate student George Volkoff at Berkeley, showed that Landau’s idea about stellar cores was not correct, but that the general idea of a neutron core, or rather neutron star, was correct [8]. Once Oppenheimer was interested in neutron stars, he kept going and asked the same question about neutron stars that Chandrasekhar had asked about white dwarfs: Is there a maximum size for neutron stars beyond which they must collapse? The answer to this question used the same quantum mechanical degeneracy pressure (now provided by neutrons rather than electrons) and gravitational compaction as the problem of white dwarfs, but it required detailed understanding of nuclear forces, which in 1938 were only beginning to be understood. However, Oppenheimer knew enough to make a good estimate of the nuclear binding contribution to the total internal pressure and came to a similar conclusion for neutron stars as Chandrasekhar had made for white dwarfs. There was indeed a maximum mass of a neutron star, a Chandrasekhar-type limit of about three solar masses. Beyond this mass, even the degeneracy pressure of neutrons could not support gravitational pressure, and the neutron star must collapse. In Oppenheimer’s mind it was clear what it must collapse to—a black hole (known as gravitational cut-off at that time). This was to lead Oppenheimer and John Wheeler to their famous confrontation over the existence of black holes, which Oppenheimer won, but Wheeler took possession of the battle field [9].
Derivation of the Relativistic Chandrasekhar Limit
White dwarfs are created from the balance between gravitational compression and the degeneracy pressure of electrons caused by the Pauli exclusion principle. When a star collapses gravitationally, the matter becomes so dense that the electrons begin to fill up quantum states until all the lowest-energy states are filled and no more electrons can be added. This results in a balance that stabilizes the gravitational collapse, and the result is a white dwarf with a mass density a million times larger than the Sun.
If the electrons remained non-relativistic, then there would be no upper limit for the size of a star that would form a white dwarf. However, because electrons become relativistic at high enough compaction, if the initial star is too massive, the electron degeneracy pressure becomes limited relativistically and cannot keep the matter from compacting more, and even the white dwarf will collapse (to a neutron star or a black hole). The largest mass that can be supported by a white dwarf is known as the Chandrasekhar limit.
A simplified derivation of the Chandrasekhar limit begins by defining the total energy as the kinetic energy of the degenerate Fermi electron gas plus the gravitational potential energy
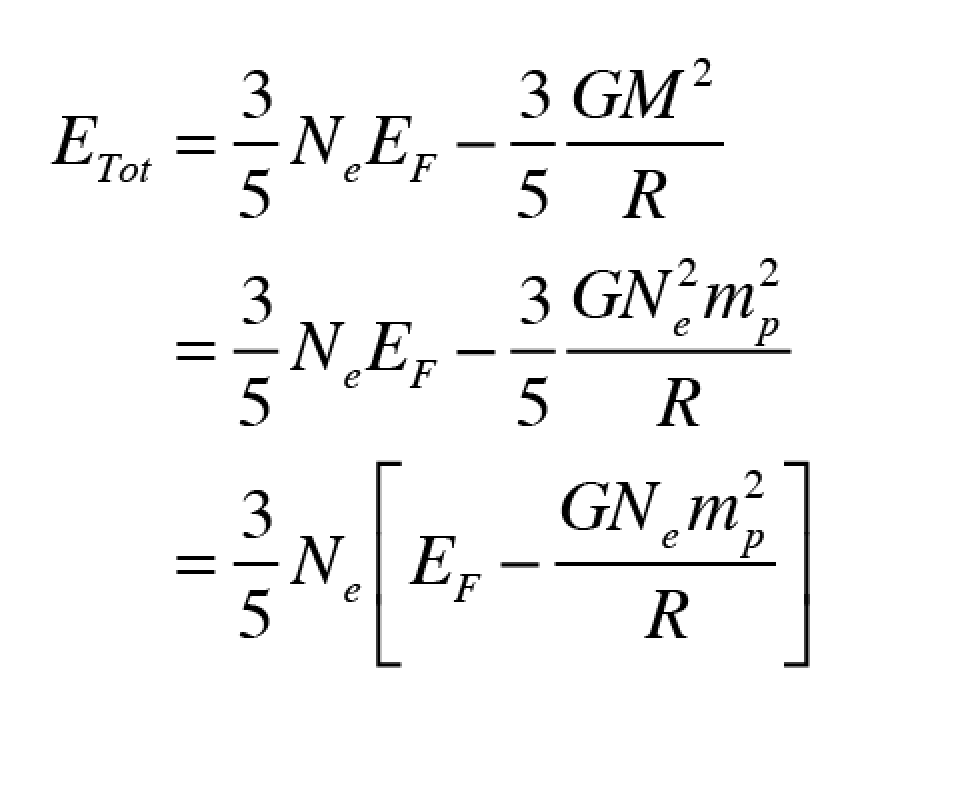
The kinetic energy of the degenerate Fermi gas has the relativistic expression

where the Fermi k-vector can be expressed as a function of the radius of the white dwarf and the total number of electrons in the star, as

If the star is composed of pure hydrogen, then the mass of the star is expressed in terms of the total number of electrons and the mass of the proton

The total energy of the white dwarf is minimized by taking its derivative with respect to the radius of the star

When the derivative is set to zero, the term in brackets becomes

This is solved for the radius for which the electron degeneracy pressure stabilizes the gravitational pressure

This is the relativistic radius-mass expression for the size of the stabilized white dwarf as a function of the mass (or total number of electrons). One of the astonishing results of this calculation is the merging of astronomically large numbers (the mass of stars) with both relativity and quantum physics. The radius of the white dwarf is actually expressed as a multiple of the Compton wavelength of the electron!
The expression in the square root becomes smaller as the size of the star increases, and there is an upper bound to the mass of the star beyond which the argument in the square root goes negative. This upper bound is the Chandrasekhar limit defined when the argument equals zero

This gives the final expression for the Chandrasekhar limit (expressed in terms of the Planck mass)

This expression is only approximate, but it does contain the essential physics and magnitude. This limit is on the order of a solar mass. A more realistic numerical calculation yields a limiting mass of about 1.4 times the mass of the Sun. For white dwarfs larger than this value, the electron degeneracy is insufficient to support the gravitational pressure, and the star will collapse to a neutron star or a black hole.
By David D. Nolte, Jan. 7, 2019
[1] The fact that Eddington coordinates removed the singularity at the Schwarzschild radius was first pointed out by Lemaitre in 1933. A local observer passing through the Schwarzschild radius would experience no divergence in local properties, even though a distant observer would see that in-falling observer becoming length contracted and time dilated. This point of view of an in-falling observer was explained in 1958 by Finkelstein, who also pointed out that the Schwarzschild radius is an event horizon.
[2] William Herschel (1803), Account of the Changes That Have Happened, during the Last Twenty-Five Years, in the Relative Situation of Double-Stars; With an Investigation of the Cause to Which They Are Owing, Philosophical Transactions of the Royal Society of London 93, pp. 339–382 (Motion of binary stars)
[3] Boss, L. (1910). Preliminary General Catalogue of 6188 stars for the epoch 1900. Carnegie Institution of Washington. (Mass and radius of Sirius B)
[4] Eddington, A. S. (1927). Stars and Atoms. Clarendon Press. LCCN 27015694.
[5] Fowler, R. H. (1926). “On dense matter”. Monthly Notices of the Royal Astronomical Society 87: 114. Bibcode:1926MNRAS..87..114F. (Quantum mechanics of degenerate matter).
[6] Chandrasekhar, S. (1931). “The Maximum Mass of Ideal White Dwarfs”. The Astrophysical Journal 74: 81. Bibcode:1931ApJ….74…81C. doi:10.1086/143324. (Mass limit of white dwarfs).
[7] Kip Thorne (1994) Black Holes & Time Warps: Einstein’s Outrageous Legacy (Norton). pg. 174
[8] Oppenheimer was aware of Zwicky’s proposal because he had a joint appointment between Berkeley and Cal Tech.
[9] See Chapter 7, “The Lens of Gravity” in Galileo Unbound: A Path Across Life, the Universe and Everything (Oxford University Press, 2018).

