Niels Bohr’s atom, by late 1925, was a series of kludges cobbled together into a Rube Goldberg type of construction.  On the one hand, there was the Bohr-Sommerfeld quantization conditions that let Bohr’s originally circular orbits morph into ellipses like planets in the solar system.  On the other hand, there was Pauli’s exclusion principle that partially explained the building up of electron orbits in many-electron atoms, but to many it seemed like an ad hoc rule. 

The time was ripe for a new perspective. Enter the wunderkind, Werner Heisenberg.

Heisenberg’s Trajectory

Werner Heisenberg (1901 – 1976) was the golden boy—smart, dashing, ambitious. He excelled at everything he did and was a natural leader among his group of young friends. He entered the University of Munich in 1920 at the age of 19 to begin working towards his doctorate degree in mathematics, but he quickly became entranced with an advanced seminar course given by Arnold Sommerfeld (1868 – 1951) on quantum mechanics. His studies under Sommerfeld advanced quickly, and he was proficient enough to be “lent out” to the group of Max Born and David Hilbert at the University of Göttingen for the 1922-1923 semester when Sommerfeld was on sabbatical at the University of Wisconsin, Madison, in the United States. Born was impressed with the young student and promised him a post-doc position upon his graduation with a doctoral degree in theoretical physics the next year (when Heisenberg would be just 22 years old).

Unfortunately, his brilliantly ascending career ran headlong into “Willy” Wien who had won the Nobel Prize in 1911 for his displacement law of black body radiation. Wien was a hard-baked experimentalist who had little patience with the speculative flights of theoretical physics. Heisenberg, in contrast, had little patience with the mundane details of experimental science. The two were heading for an impasse.

The collision came during the oral examination for Heisenberg’s doctoral degree. Wien, determined to put Heisenberg in his place, opened with a difficult question about experimental methods. Heisenberg could not answer, so Wien asked a slightly less difficult but still detailed question that Heisenberg also could not answer. The examination went on like this until finally Wien asked Heisenberg to derive the resolving power of a simple microscope. Heisenberg was so flustered by this time that he could not do even that. Wien, in disgust, turned to Sommerfeld and pronounced a failing grade for Heisenberg. After Heisenberg stepped out of the room, the professors wrangled over the single committee grade that would need to be recorded. Sommerfeld’s top grade for Heisenberg’s mathematical performance and Wien’s bottom grade for his experimental performance led to the compromise grade of a “C” for the exam—the minimum grade sufficient to pass.

Heisenberg was mortified. Accustomed always to excelling and being lauded for his talents, Heisenberg left town that night, taking the late train to Göttingen where a surprised Born found him outside his office early the next morning—fully two months ahead of schedule. Heisenberg told him everything and asked if Born would still have him. After learning more about Wien’s “ambush”, Born assured Heisenberg that he still had a place for him.

Heisenberg was so successful at Göttingen, that when Born planned to spend a year sabbatical at MIT in the United States for the 1924-1925 semester, Heisenberg was “lent out” to Niels Bohr in Copenhagen. While there, Heisenberg, Bohr, Pauli and Kramers had intense discussions about the impending crisis in quantum theory. Bohr was fully aware of the precarious patches that made up the quantum theory of the many-electron atom, and the four physicists attempted to patch it yet again with a theoretical effort led by Kramers to try to reconcile optical transitions in the atomic spectra. But no one was satisfied, and the theory had serious internal inconsistencies, not the least of which was a need to sacrifice the sacrosanct principle of conservation of energy.

Through it all, Heisenberg was thrilled by his deep involvement in the most fundamental questions of physics of the day and was even more thrilled by his interactions with the great minds he found in Copenhagen. When he returned to Göttingen on April 27, 1925, the arguments and inconsistencies were ringing in his head, infecting the group at Göttingen with the challenging physics, especially Max Born and Pascual Jordan.

Little headway could be made, until Heisenberg had a serious attack of hay fever that sent him for respite on June 7 to the remote island of Helgoland in the North Sea far off of the coast from Bremerhaven. The trip cleared Heisenberg’s head—literally and figuratively—as he had time to come to grips with the core difficulties of quantum theory.

Trajectory’s End

The Mythology of Physics recounts the tale of when Heisenberg had his epiphany, watching from the beach as the sun rose over the sea. The repeated retelling has solidified the moment into revealed “truth”, but the origins are probably more prosaic. Strip a problem bare of all its superficial coverings and what remains must be the minimal set of what can be known. Yet to do so requires courage, for much of the superficial coverings are established dogma, embedded so deeply in the thought of the day that angry reactions must be expected.

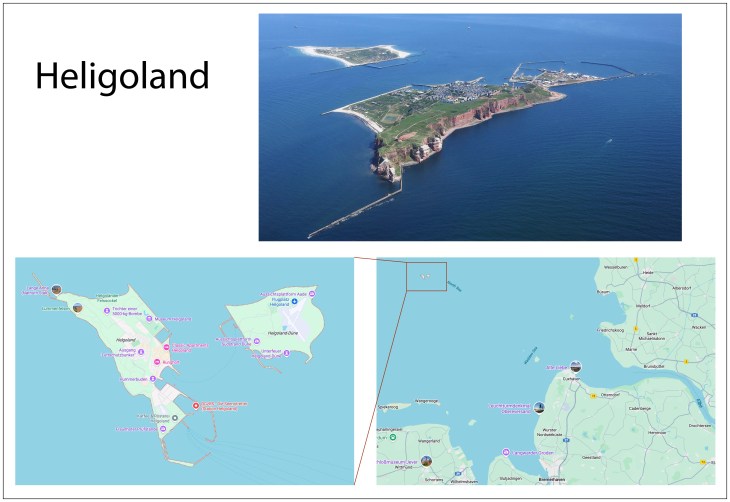
At some moment, Heisenberg realized that the superficial covering of atomic theory was the slavish devotion to the electron trajectory—to the Bohr-Sommerfeld electron orbits. Ever since Kepler, the mental image of masses in orbit around their force center had dominated physical theory. Quantum theory likewise was obsessed with images of trajectories—it persists to this day in the universal logo of atomic energy. Heisenberg now rejected this image as unknowable and hence not relevant for a successful theory. But if electron orbits were out, what was the minimal set of what can be known to be true? Heisenberg decided that it was simply the wavelengths and intensities of light absorbed and emitted by atoms. But what then? How do you create a theory constructed on transition energies and intensities alone? The epiphany was the answer—construct a dynamics by which the quantum system proceeds step-by-step, transition-by-transition, while retaining the sacrosanct energy conservation that had been discarded by Kramer’s unsuccessful theory.

The result, after returning to Göttingen, is Heisenberg’s paper, submitted July 29, 1925 to Zeitschrift für Physik titled Über quantentheoretische Umdeutung kinematischer und mechanischer Beziehungen (Over the quantum theoretical meaning of kinematic and mechanical relationships).

Heisenberg begins with the fundamental energy relationship between the frequency of light and the energy difference in a transition

His goal is to remove the electron orbit from the theory, yet positions cannot be removed entirely, so he takes the step of transforming position into a superposition of amplitudes with frequencies related to the optical transitions.

Armed with the amplitude coefficients and the transition frequencies, he constructs sums of transitions that proceed step by step between initial and final states.

After introducing the electric field, Heisenberg calculates the polarizability of the atom, the induced moment, using Kramer’s dispersion formula combined with his new superposition.

Heisenberg applied his new theoretical approach to one-dimensional quantum systems, using as an explicit example the anharmonic oscillator, and it worked! Heisenberg had invented a new theoretical approach to quantum physics that relied only on transition frequencies and amplitudes—only what could be measured without any need to speculate on what types of motions electrons might be executing. Heisenberg published his new theory on his own, as sole author befitting his individual breakthrough. Yet it was done under the guidance of his supervisor Max Born, who recognized something within Heisenberg’s mathematics.

The Matrix

Heisenberg’s derivations involved numerous summations as amplitudes multiplied amplitudes in complicated sequences. The mathematical steps themselves were straightforward—just products and sums—but the numbers of permutations were daunting, and their sequential order mattered, requiring skill and care not to miss terms or to get minus signs wrong.

Yet Born recognized within Heisenberg’s mathematics the operations of matrix multiplication. The different permutations with sums of alternating signs were exactly what one obtained by taking determinants of matrices, and it was well known that the order of matrix multiplication mattered, where a*b ≠ b*a. With his assistant Pacual Jordan, the two reworked Heisenberg’s paper in the mathematical language of matrices, submitting their “mirror” paper to Zeitschrift on Sept. 27, 1925. Their title was prophetic: Towards Quantum Mechanics. This was the first time that the phrase “quantum mechanics” was used to encompass all of the widely varying aspects of quantum systems.

In the abstract, they state:

The approaches recently put forward by Heisenberg (initially for systems with one degree of freedom) are developed into a systematic theory of quantum mechanics. The mathematical tool is matrix calculus. After this is briefly outlined, the mechanical equations of motion are derived from a variational principle, and the proof is carried out that, on the basis of Heisenberg’s quantum condition, the energy theorem and Bohr’s frequency condition follow from the mechanical equations.  Using the example of the anharmonic oscillator, the question of the uniqueness of the solution and the significance of the phases in the partial oscillations are discussed.  The conclusion describes an attempt to incorporate the laws of the electromagnetic field into the new theory.

Born and Jordan begin by creating a matrix form for the Hamiltonian subject to Hamilton’s dynamical equations

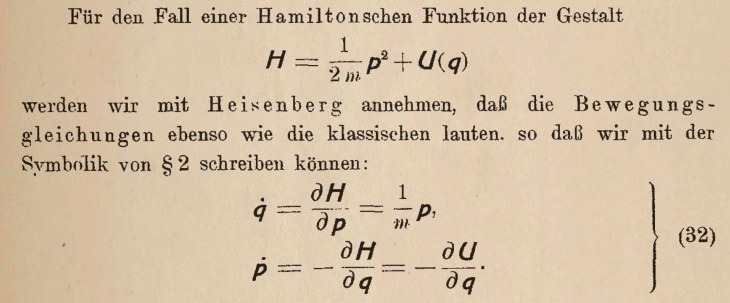
Armed with matrix quantities for position and momentum, Born and Jordan construct the commutator of p with q to arrive at one of the most fundamental quantum relationships: the non-zero difference in the permuted products related to Planck’s constant. This commutation relationship would become the foundation for many quantum theories to come.

As Heisenberg had done in his paper, Born and Jordan introduce the electric field of light to derive the dispersion of an atomic gas.

The Born and Jordan paper appeared in the November issue of Zeitschrift für Physik, although a pre-print was picked up in England by Paul Dirac, who was working towards his doctoral degree under the mentorship of Ralph Fowler (1889 – 1944) at Cambridge. Dirac was deeply knowledgable in classical mechanics, and he recognized as soon as he saw it that the new quantum commutator was intimately connected to a quantity in classical mechanics known as a Poisson bracket. The Poisson bracket is part of Hamiltonian mechanics that defines how two variables, known as conjugate variables, are connected. For instance, the Poisson bracket of x with px is non-zero, meaning that these are conjugate variables, while the Poisson bracket of x with py is zero, meaning that these variables are fully independent. Conjugate variables are not “dependent” in an algebraic sense, but are linked through the structure of Hamilton’s equations—they are the “p’s and q’s” of phase space.

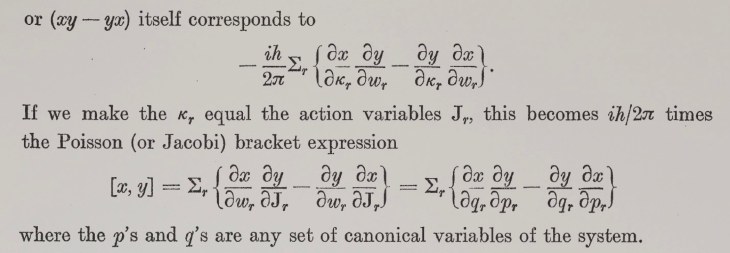
Dirac submitted a paper on Nov. 7, 1925 to the Proceedings of the Royal Society of London where he showed that the Heisenberg commutator (a quantum quantity) directly proportional to the Poisson bracket (the classical quantity) with a proportionality factor that depended on Planck’s constant.

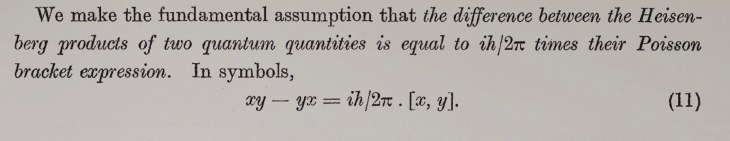
The Drei-Männer Quantum Mechanics Paper: Born, Heisenberg, and Jordan

Meanwhile, back in Göttingen, the three quantum physicists Born, Heisenberg and Jordan now combined forces to write a third foundational paper that established the full range of the new matrix mechanics. Heisenberg’s first paper had been the insight. Born and Jordan’s following paper had re-expressed Heistenberg’s formulas into matrix algebra. But both papers had used simple one-dimensional problems as test examples. Working together, they extended the new quantum mechanics to systems with many degrees of freedom.

With this paper, the matrix properties of dynamical variables are defined and used in their full form.

With the theory out in the open, Pauli in Hamburg and Dirac at Cambridge used the new quantum mechanics to derive the transition energies of hydrogen, while Lucy Mensing and J. Robert Oppenheimer in Göttingen extended it to the spectra of more complicated molecules.

Open Issues

Heisenberg’s matrix mechanics might have exclusively taken hold of the quantum theory community and we would all be using matrices today to perform all our calculations. But within one month of the success of matrix mechanics, an alternative quantum theory would be proposed by Erwin Schrödinger based on waves, a theory that came to be called wave mechanics. There was a minor battle fought over matrix mechanics versus wave mechanics, but in the end, Bohr compromised with his complementarity principle, allowing each to stand as equivalent viewpoints of quantum phenomena (but more about Schrödinger and his waves in my next Blog).

Further Reading

For more stories about the early days of quantum physics read Chapter 8, “On the Quantum Footpath” in D. D. Nolte, “Galileo Unbound: A Path Across Life, the Universe and Everything” (Oxford University Press, 2018)

For definitive accounts of Heisenberg’s life see D. Cassidy “Beyond Uncertainty: Heisenberg, Quantum Physics and the Bomb” (Bellevue Press, 2009)

References

[1] Heisenberg, W. (1925). “Über quantentheoretische Umdeutung kinematischer und mechanischer Beziehungen”. Zeitschrift für Physik, 33(1), 879–893.

[2] Born, M., & Jordan, P. (1925). “Zur Quantenmechanik”. Zeitschrift für Physik, 34(1), 858–888.

[3] Dirac, P. A. M. (1925). The fundamental equations of quantum mechanics. Proceedings of the Royal Society of London. Series A, Containing Papers of a Mathematical and Physical Character, 109(752), 642–653

[4] Born, M., W. Heisenberg and P. Jordan (1926). “Quantum mechanics II.” Zeitschrift Fur Physik, 35, (8/9): 557–615.

[5] Dirac, P. A. M. (1926). “Quantum mechanics and a preliminary investigation of the hydrogen atom.” Proceedings of the Royal Society of London Series A, 110(755): 561–79.

[6] Pauli, W. (1926). “The hydrogen spectrum from the view point of the new quantal mechanics.” Zeitschrift Fur Physik, 36(5): 336–63.

[7] Mensing, L. (1926). “Die Rotations-Schwingungsbanden nach der Quantenmechanik”. Zeitschrift für Physik, 36(11), 814–823.

[8] Born, M., & Oppenheimer, J. R. (1927). “Zur Quantentheorie der Molekeln”. Annalen der Physik, 389(20), 457–484.