The tortoise and the hare. The snail and the falcon. The sloth and the cheetah.
Comparing the slowest animals to the fastest, the peregrine falcon wins in the air at 200 mph diving on a dove. The cheetah wins on the ground at 75 mph running down dinner. That’s fast!
Einstein’s theory of relativity says that fast things behave differently than slow things. So how fast do things need to move to see these effects?
The measure is the ratio of the speed of the object relative to the speed of light at 670 million miles per hour. This ratio is called beta
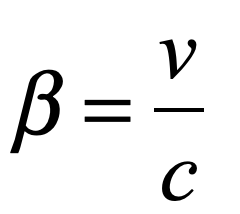
The cheetah has β = 1×10-7, and the peregrine falcon has β = 4×10-7—which are less than one part in a million.
And what about that snail? At a speed of 0.003 mph it has β = 4×10-12 for a just few parts per trillion.
Yet relativistic physics is present in biology, despite these slow speeds, and they can help keep us alive. How?
The Boon and Bane of Oxygen
All animal life on Earth needs oxygen to survive. Oxygen is the energy storehouse that fuels mitochondria—the tiny batteries inside our cells that generate the energetic molecules that make us run.
Of all the elements, oxygen is second only to flourine as the most chemically reactive. But fluorine is too one-dimensional to help much with life. It needs only one extra electron to complete its outer-shell octet, leaving nothing in reserve to attach to much else. Oxygen, on the other hand, needs two electrons to complete its outer shell, making it an easy bridge between two other atoms, usually carbons or hydrogens, and there you have it—organic chemistry is off and running.
Yet the same chemical reactivity that makes oxygen central to life also makes it corrosive to life. When oxygen is not doing its part keeping things alive, it is tearing things apart.
The problem is reactive oxygen species, or ROS. These are activated forms of oxygen that damage biological molecules, including DNA, putting wear and tear on (aging) the cellular machinery and introducing mutations into the genetic codes. And one of the ROS is an active form of simple diatomic oxygen O2 — the very air we breathe.
The Saga of the Singlet and the Triplet
Diatomic oxygen is deceptively simple: two oxygen atoms, each two electrons short of a full shell, coming together to share two of each other’s electrons in a double bond, satisfying the closed shell octet for the outer valence electrons for this element.
Bonds are based on energy levels, and the individual energy levels of the two separate oxygen atoms combine and shift as they form molecular orbitals (MO). These orbitals are occupied by the 6 + 6 = 12 electrons of the diatomic molecule. The first 10 electrons fill up the lower MOs until the last two go into the next highest state. Here, for interesting reasons associated with how electrons interact with each other in confined spaces, the last two electrons both have the same orientation of their spins. The total electron spin of the final full ground-state configuration of 12 electrons has S = 1.
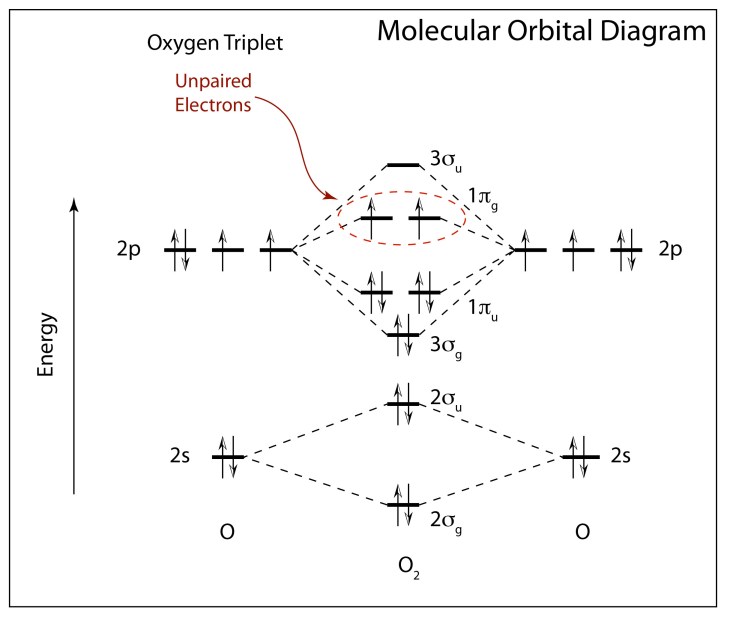
When a many-electron system has a spin S = 1, quantum mechanics prescribes that it has 2S+1 spin projections, so that the ground state of diatomic oxygen has three possible spin projections—known as a triplet. But this is just for the lowest energy configuration of O2.
It is also possible to put both electrons into the final levels with opposite spins, giving S = 0. This is known as the singlet, and there are two different ways these spins can be anti-aligned, creating two excited states. The first excited state is about 1 eV in energy above the ground state, and the second excited state is about 0.7 eV higher than the first.
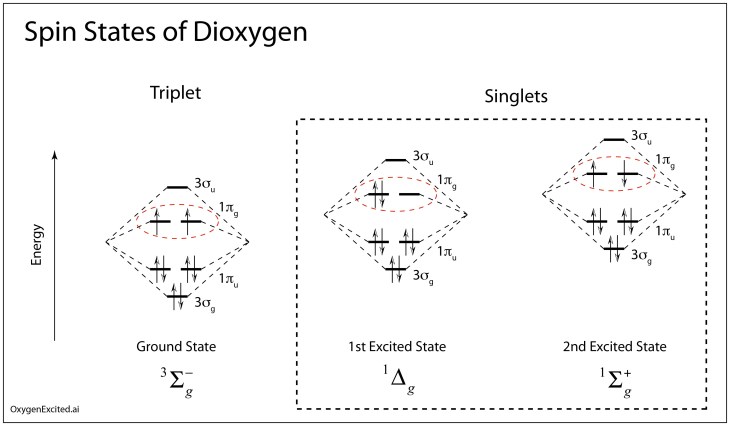
Now we come the heart of our story. It hinges on how reactive the different forms of O2 are, and how easily the singlet and the triplet can transform into each other.
Don’t Mix Your Spins
What happens if you mix hydrogen and oxygen in a 2:1 ratio in a plastic bag?
Nothing! Unless you touch a match to it, and then it “pops” and creates water H2O.
Despite the thermodynamic instability of oxygen and hydrogen, the mixture is kinetically stable because it takes an additional input of energy to make the reaction go. This is because oxygen at room temperature is almost exclusively in its ground state, the triplet state. The triplet oxygen accepts electrons from other molecules, or atoms like hydrogen, but the local environment of organic molecules are almost exclusively in S = 0 states because of their stability. To accept two electrons from organic molecules requires spins to flip, which has an energy associated with the process, creating an energy barrier. This is known as the spin conservation rule of organic chemistry. Therefore, the reaction with the triplet is unlikely to go, unless you give it a hand with extra energy or a catalyst to get over the barrier.
However, this “spin blockade” that makes triplet (S = 1) oxygen unreactive (kinetically stable) is lifted in the case of singlet (S = 0) oxygen. The singlet still accepts two electrons from other molecules, but these can be taken up easily by accepting electrons from the S = 0 organic molecules around it, conserving spin. This makes singlet oxygen extremely reactive organically and hence is why it is an ROS. Singlet oxygen reacts with organic molecules, damaging them.
Despite the deleterious effects of singlet oxygen, it is produced as a side effect of lipids (fats) immersed in an oxygen environment. In a sense, fat slowly “burns”, creating reactive organic species that further react with lipids (primarily polyunsaturated fatty acids (PUFAs)), generating more ROS and creating a chain reaction. The chain reaction is terminated by the Russell mechanism that generates singlet oxygen as a byproduct.
Singlet oxygen, even though it is an excited state, cannot convert directly back to the benign triplet ground state for the same spin conservation reasons as organic chemistry. The singlet (S = 0) cannot emit a photon to get to its ground state triplet (S = 1) because photons cannot change the spin of the electrons in a transition. So once the singlet oxygen is formed, it can stick around and react chemically, eating up an organic molecule. Therefore, the oxygen environment, so necessary for our survival, is slowly killing us with oxydative stress. In response, mechanisms to de-excite singlet oxygen evolved, using organic molecules like carotenoids that are excellent physical quenchers of the singlet state.
But let’s flip the problem and ask what it takes to selectively harness singlet oxygen production to act as a targeted therapy that kills cancer cells—Enter Einstein’s theory of special relativity.
Relativistic Origins of Spin-Orbit Coupling
When I was a sophomore at Cornell University in the late 1970’s, I took the introductory class in electricity and magnetism. The text was an oddball thing from the Berkeley Physics Series authored by the Nobel Laureate, Edward Purcell, from Harvard.
(The Berkeley Series was a set of 5 volumes to accompany a 5-semester introduction to physics. It was the brainchild of Charles Kittel from Berkeley and Philip Morrison from Cornell who, in 1961, were responding to the Sputnik crisis and the need to improve the teaching of physics in the West.)
Purcell’s book had the quirky misfortune to use Gaussian units based on centimeters and grams (cgs) instead of meters and kilograms (MKS). Physicists tend to like cgs units, especially in the teaching of electromagnetism, because it places electric fields and magnetic fields on equal footing. Unfortunately, it creates a weird set of units like “statvolts” and “statcoulombs” that are a nightmare to calculate with.
Nonetheless, Purcell’s book was revolutionary as a second-semester intro physics book, in that it used Special Relativity to explain the transformations between electric and magnetic fields. For instance, starting with the static electric field of a stationary parallel plate capacitor in one frame, Purcell showed how an observer moving relatively to the capacitor in a moving frame detects the electric field as expected, but also detects a slight magnetic field. As the speed of the observer increases, the strength of the magnetic field increases, becoming comparable to the electric field in strength as the relative frame speed approaches the speed of light.
In this way, there is one frame in which there is no magnetic field at all, and another frame in which there is a strong magnetic field. The only difference is the point of view—yet the consequences are profound, especially when the quantum spin of an electron is involved.
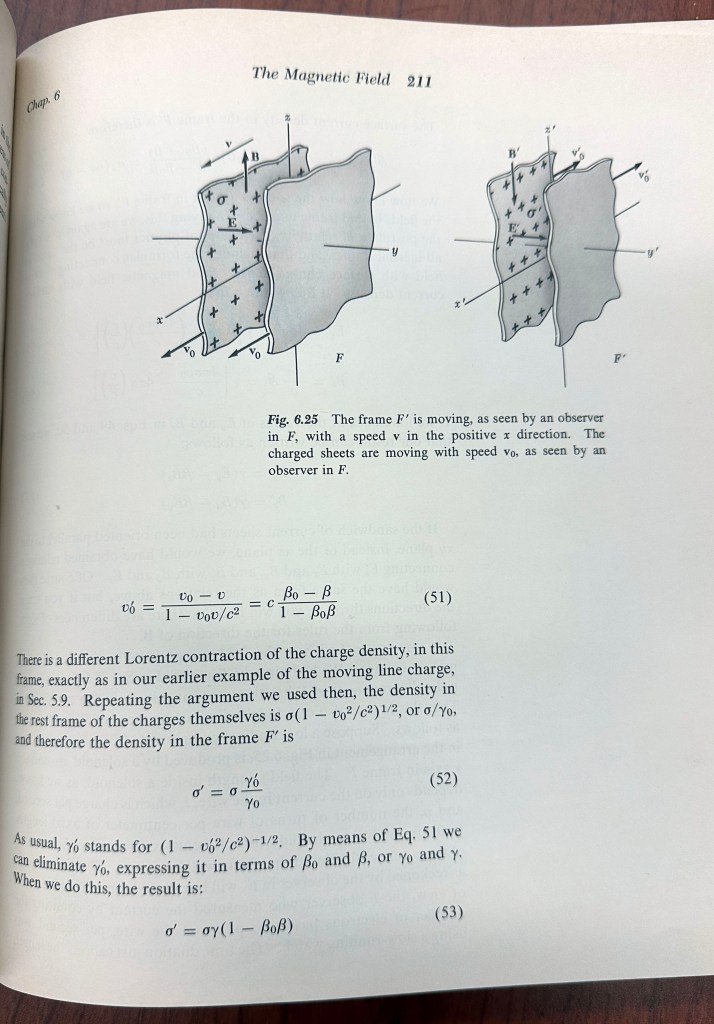
The spin of the electron is like a tiny magnet, and if the spin is in an external magnetic field, it feels a torque as well as an interaction energy. The torque makes it precess, and the interaction energy shifts its energy levels depending on the orientation of the spin to the field.
When an electron is in a quantum orbital around a stationary nucleus, attracted by the electric field of the nucleus, it would seem that there is no magnetic field for the spin to interact with, which indeed is true if the electron has no angular momentum. But if the electron orbital does have angular momentum with a non-zero expectation value for its velocity, then this moving electron does experience a magnetic field—the electron is moving relative to the electric field of the nucleus, and special relativity dictates that it experiences a magnetic field. The resulting magnetic field interacts with the magnetic moment of the electron and shifts its energy a tiny amount.
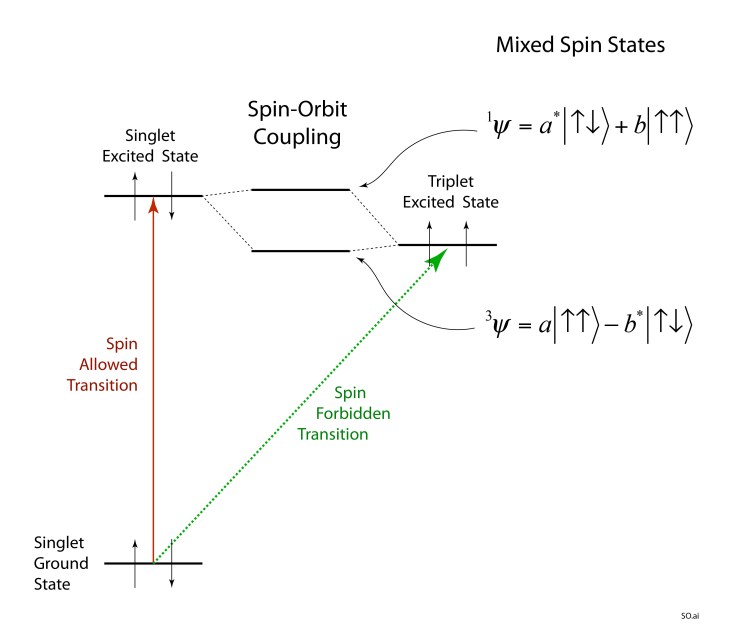
This is called the spin-orbit interaction and leads to the fine structure of the electron energy levels in atoms and molecules. More importantly for our story of Singlets and Triplets, the slight shift in energy also mixes the spin states. Quantum mechanical superposition of states mixes in a little S = 0 into the triplet excited state and a little S = 1 into the singlet ground state, and the transition is no longer strictly spin forbidden. The spin-orbit effect is relatively small in oxygen, contributing little to the quenching of singlet oxygen. But spin-orbit in other molecules, especially optical dyes that absorb light, can be used to generate singlet oxygen as a potent way to kill cancer cells.
Spin-Orbit and Photodynamic Cancer Therapy
The physics of light propagation through living tissue is a fascinating topic. Light is easily transported through tissue through multiple scattering. This is why your whole hand glows red when you cover a flashlight at night. The photons bounce around but are not easily absorbed. This surprising translucence of tissue can be used to help treat cancer.
Photodynamic cancer therapy uses photosensitizer molecules, typically organic dyes, that absorb light, transforming the molecule from a single ground state to a singlet excited state (spin-allowed transition). Although singlet-to-triplet conversion is spin-forbidden, the spin-orbit coupling slightly mixes the spin states which allows a transformation known as intersystem crossing (ISC). The excited singlet crosses over (usually through a vibrational state associated with thermal energy) to an excited triplet state of the photosensitizer molecule. Oxygen triplet molecules, that are always prevalent in tissue, collide with the triplet photosensitizer—and they swap their energies in a spin-allowed transfer. The photosensitizer triplet returns to its singlet ground state, while the triplet oxygen converts to highly reactive singlet oxygen. The swap doesn’t change total spin, so it is allowed and fast, generating large amounts of reactive oxygen singlets.
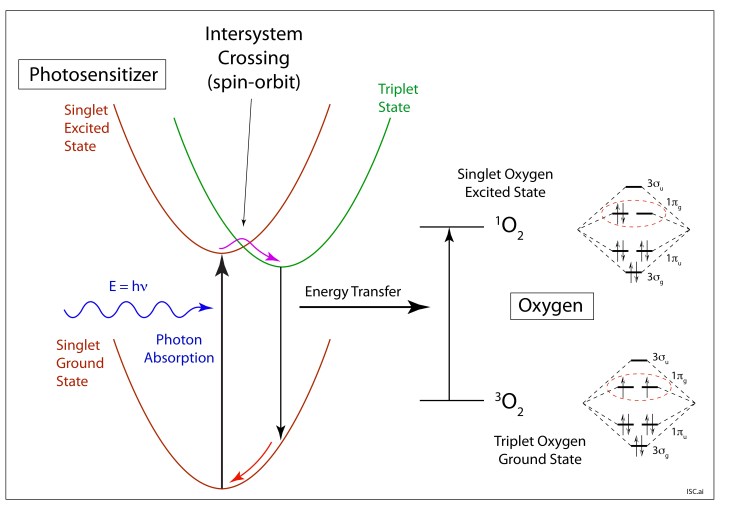
In photodynamic therapy, the photosensitizer is taken up by the patient’s body, but the doctor only shines light around the tumor area, letting the light multiply-scatter through the tissue, exciting the photosensitizer and locally producing singlet oxygens that kill the local cancer cells. Other parts of the body remain in the dark and have none of the ill-effects that are so common for the conventional systemic cytotoxic anti-cancer drugs. This local treatment of the tumor using localized light can be much more benign to overall patient health while still delivering effective treatment to the tumor.
Photodynamic therapy has been approved by the FDA for some early stage cancers, and continuing research is expanding its applications. Because light transport through tissue is limited to about a centimeter, most of these applications are for “shallow” tumors that can be accessed by light through the skin or through internal surfaces (like the esophagus or colon).
Postscript: Relativistic Spin
I can’t leave this story of relativistic biology without going into a final historical detail from the early days of relativistic quantum theory. When Uhlenbeck and Goudsmit first proposed in 1925 that the electron has spin, there were two immediate objections. First, Lorentz showed that in a semiclassical model of the spinning electron, the surface of the electron would be moving at 300 times the speed of light. The solution to this problem came three years later in 1928 with the relativistic quantum theory of Paul Dirac, which took an entirely different view of quantum versus classical physics. In quantum theory, there is no “radius of the electron” as there was in semiclassical theory.
The second objection was more serious. The original predictions from electron spin and the spin-orbit interaction in Bohr’s theory of the atom predicted a fine-structure splitting that was a factor of 2 times larger than observed experimentally. In 1926 Llewellyn Thomas showed that a relativistically precessing spin was in a non-inertial frame, requiring a continuous set of transformations from one instantaneously inertial frame to another. These continuously shifting transformations introduced a factor of 1/2 into the spin precession, exactly matching the experimental values. This effect is known as Thomas precession. Interestingly, the fully relativistic theory of Dirac in 1928 automatically incorporated this precession within the theory, so once again Dirac’s equation superseded the old quantum theory.
Galileo Unbound 