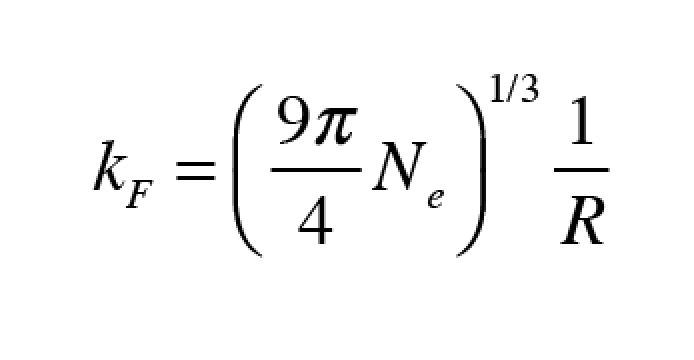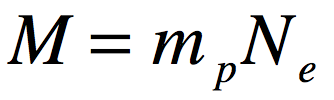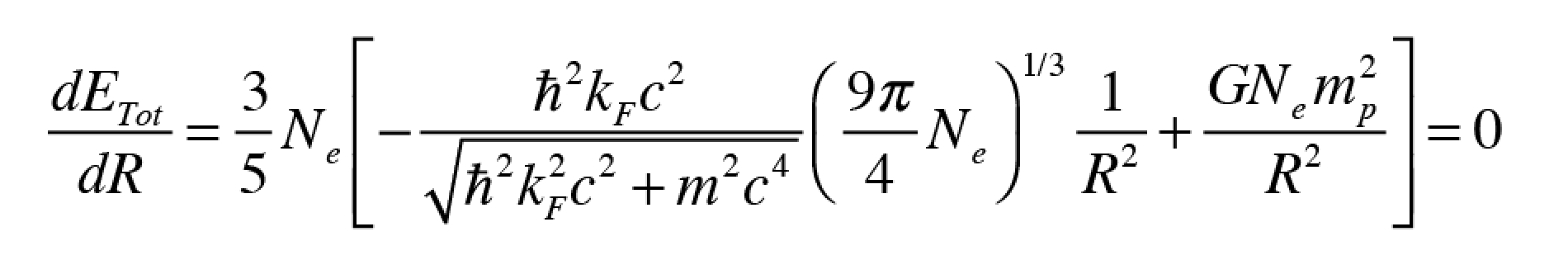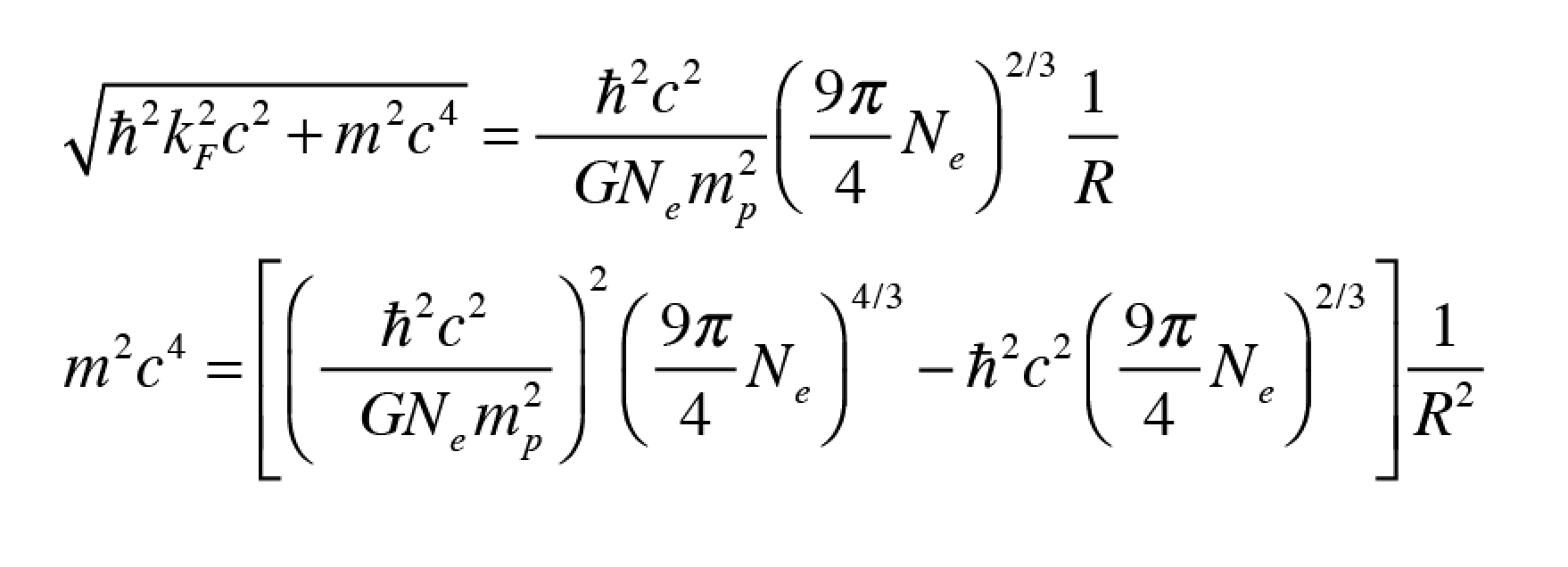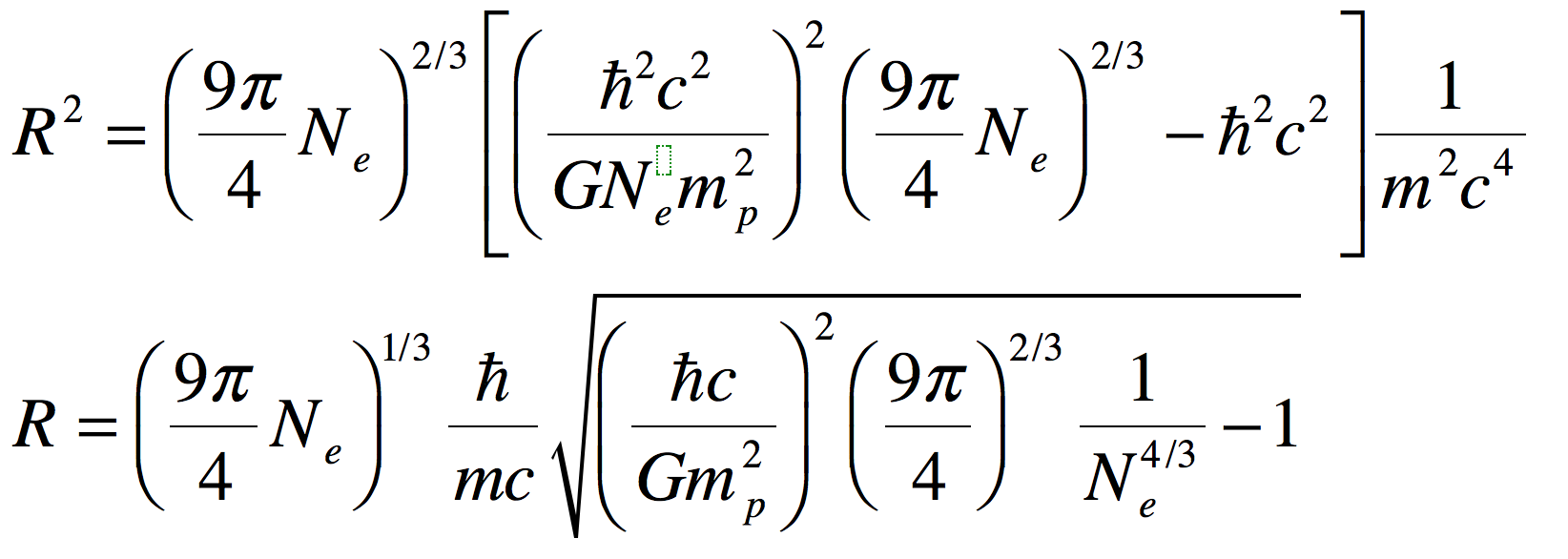In the fall semester of 1947, a brilliant young British mathematician arrived at Cornell University to begin a yearlong fellowship paid by the British Commonwealth. Freeman Dyson (1923 –) had received an undergraduate degree in mathematics from Cambridge University and was considered to be one of their brightest graduates. With strong recommendations, he arrived to work with Hans Bethe on quantum electrodynamics. He made rapid progress on a relativistic model of the Lamb shift, inadvertently intimidating many of his fellow graduate students with his mathematical prowess. On the other hand, someone who intimidated him, was Richard Feynman.
Initially, Dyson considered Feynman to be a bit of a buffoon and slacker, but he started to notice that Feynman could calculate QED problems in a few lines that took him pages.

I think like most science/geek types, my first introduction to the unfettered mind of Freeman Dyson was through the science fiction novel Ringworld by Larry Niven. The Dyson ring, or Dyson sphere, was conceived by Dyson when he was thinking about the ultimate fate of civilizations and their increasing need for energy. The greatest source of energy on a stellar scale is of course a star, and Dyson envisioned an advanced civilization capturing all that emitted stellar energy by building a solar collector with a radius the size of a planetary orbit. He published the paper “Search for Artificial Stellar Sources of Infra-Red Radiation” in the prestigious magazine Science in 1960. The practicality of such a scheme has to be seriously questioned, but it is a classic example of how easily he thinks outside the box, taking simple principles and extrapolating them to extreme consequences until the box looks like a speck of dust. I got a first-hand chance to see his way of thinking when he gave a physics colloquium at Cornell University in 1980 when I was an undergraduate there. Hans Bethe still had his office at that time in the Newman laboratory. I remember walking by and looking into his office getting a glance of him editing a paper at his desk. The topic of Dyson’s talk was the fate of life in the long-term evolution of the universe. His arguments were so simple they could not be refuted, yet the consequences for the way life would need to evolve in extreme time was unimaginable … it was a bazaar and mind blowing experience for me as an undergrad … and and example of the strange worlds that can be imagined through simple physics principles.
Initially, as Dyson settled into his life at Cornell under Bethe, he considered Feynman to be a bit of a buffoon and slacker, but he started to notice that Feynman could calculate QED problems in a few lines that took him pages. Dyson paid closer attention to Feynman, eventually spending more of his time with him than Bethe, and realized that Feynman had invented an entirely new way of calculating quantum effects that used cartoons as a form of book keeping to reduce the complexity of many calculations. Dyson still did not fully understand how Feynman was doing it, but knew that Feynman’s approach was giving all the right answers. Around that time, he also began to read about Schwinger’s field-theory approach to QED, following Schwinger’s approach as far as he could, but always coming away with the feeling that it was too complicated and required too much math—even for him!
Road Trip Across America
That summer, Dyson had time to explore America for the first time because Bethe had gone on an extended trip to Europe. It turned out that Feynman was driving his car to New Mexico to patch things up with an old flame from his Los Alamos days, so Dyson was happy to tag along. For days, as they drove across the US, they talked about life and physics and QED. Dyson had Feynman all to himself and began to see daylight in Feynman’s approach, and to understand that it might be consistent with Schwinger’s and Tomonaga’s field theory approach. After leaving Feynman in New Mexico, he travelled to the University of Michigan where Schwinger gave a short course on QED, and he was able to dig deeper, talking with him frequently between lectures.
At the end of the summer, it had been arranged that he would spend the second year of his fellowship at the Institute for Advanced Study in Princeton where Oppenheimer was the new head. As a final lark before beginning that new phase of his studies he spent a week at Berkeley. The visit there was uneventful, and he did not find the same kind of open camaraderie that he had found with Bethe in the Newman Laboratory at Cornell, but it left him time to think. And the more he thought about Schwinger and Feynman, the more convinced he became that the two were equivalent. On the long bus ride back east from Berkeley, as he half dozed and half looked out the window, he had an epiphany. He saw all at once how to draw the map from one to the other. What was more, he realized that many of Feynman’s techniques were much simpler than Schwinger’s, which would significantly simplify lengthy calculations. By the time he arrived in Chicago, he was ready to write it all down, and by the time he arrived in Princeton, he was ready to publish. It took him only a few weeks to do it, working with an intensity that he had never experienced before. When he was done, he sent the paper off to the Physical Review[1].
Dyson knew that he had achieved something significant even though he was essentially just a second-year graduate student, at least from the point of view of the American post-graduate system. Cambridge was a little different, and Dyson’s degree there was more than the standard bachelor’s degree here. Nonetheless, he was now under the auspices of the Institute for Advanced Study, where Einstein had his office, and he had sent off an unsupervised manuscript for publication without any imprimatur from the powers at be. The specific power that mattered most was Oppenheimer, who arrived a few days after Dyson had submitted his manuscript. When he greeted Oppenheimer, he was excited and pleased to hand him a copy. Oppenheimer, on the other hand, was neither excited nor pleased to receive it. Oppenheimer had formed a particularly bad opinion of Feynman’s form of QED at the conference held in the Poconos (to read about Feynman’s disaster at the Poconos conference, see my blog) half-a-year earlier and did not think that this brash young grad student could save it. Dyson, on his part, was taken aback. No one who has ever met Dyson would ever call him brash, but in this case he fought for a higher cause, writing a bold memo to Oppenheimer—that terrifying giant of a personality—outlining the importance of the Feynman theory.
Battle for the Heart of Quantum Field Theory
Oppenheimer decided to give Dyson a chance, and arranged for a series of seminars where Dyson could present the story to the assembled theory group at the Institute, but Dyson could make little headway. Every time he began to make progress, Oppenheimer would bring it crashing to a halt with scathing questions and criticisms. This went on for weeks, until Bethe visited from Cornell. Bethe by then was working with the Feynman formalism himself. As Bethe lectured in front of Oppenheimer, he seeded his talk with statements such as “surely they had all seen this from Dyson”, and Dyson took the opportunity to pipe up that he had not been allowed to get that far. After Bethe left, Oppenheimer relented, arranging for Dyson to give three seminars in one week. The seminars each went on for hours, but finally Dyson got to the end of it. The audience shuffled out of the seminar room with no energy left for discussions or arguments. Later that day, Dyson found a note in his box from Oppenheimer saying “Nolo Contendre”—Dyson had won!
With that victory under his belt, Dyson was in a position to communicate the new methods to a small army of postdocs at the Institute, supervising their progress on many outstanding problems in quantum electrodynamics that had resisted calculations using the complicated Schwinger-Tomonaga theory. Feynman, by this time, had finally published two substantial papers on his approach[2], which added to the foundation that Dyson was building at Princeton. Although Feynman continued to work for a year or two on QED problems, the center of gravity for these problems shifted solidly to the Institute for Advanced Study and to Dyson. The army of postdocs that Dyson supervised helped establish the use of Feynman diagrams in QED, calculating ever higher-order corrections to electromagnetic interactions. These same postdocs were among the first batch of wartime-trained theorists to move into faculty positions across the US, bringing the method of Feynman diagrams with them, adding to the rapid dissemination of Feynman diagrams into many aspects of theoretical physics that extend far beyond QED [3].
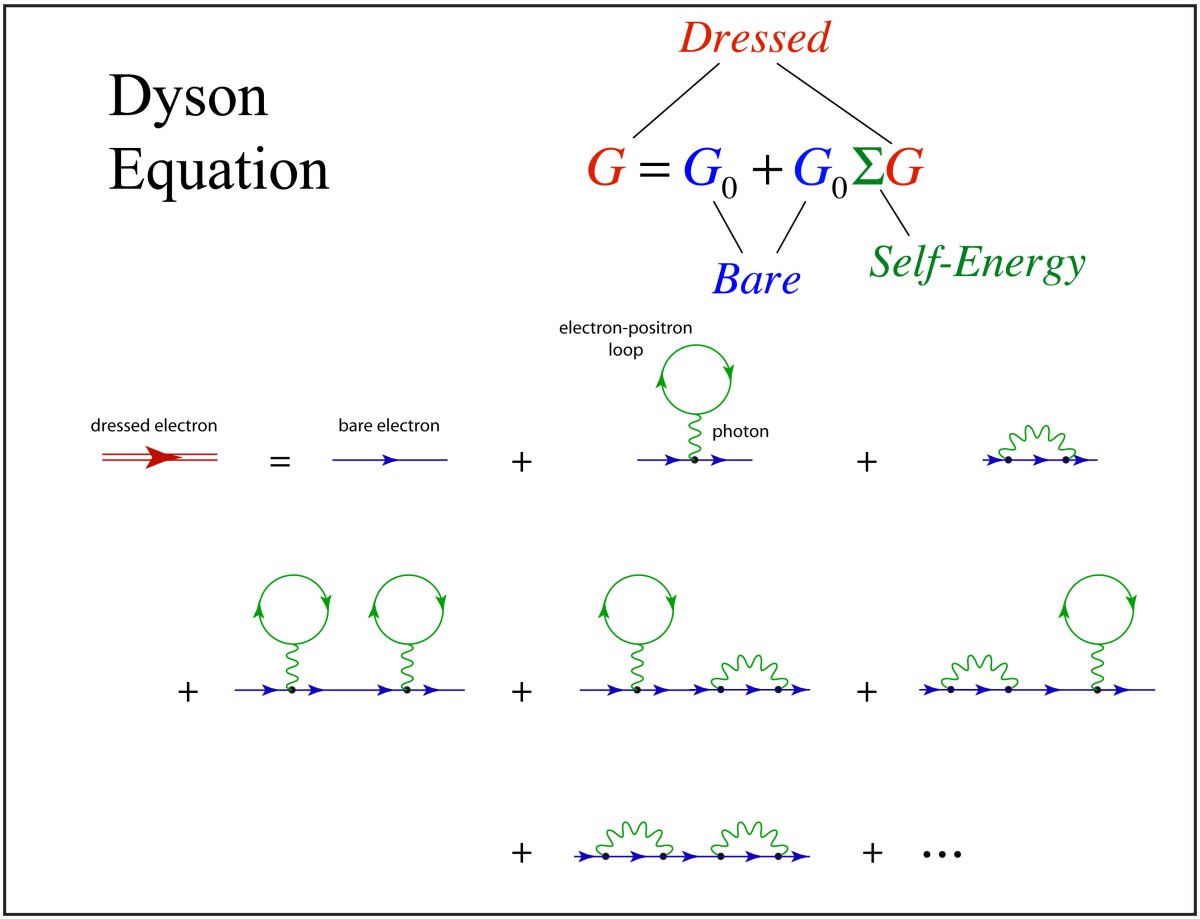
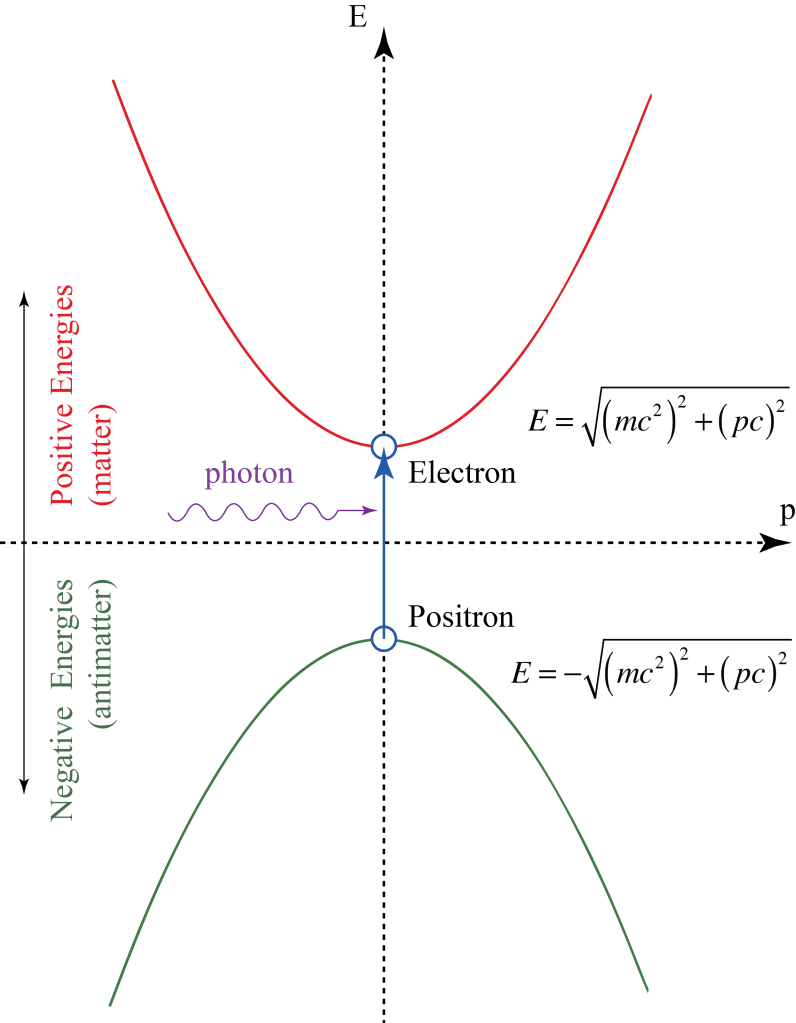
As a graduate student at Berkeley in the 1980’s I ran across a very simple-looking equation called “the Dyson equation” in our graduate textbook on relativistic quantum mechanics by Sakurai. The Dyson equation is the extraordinarily simple expression of an infinite series of Feynman diagrams that describes how an electron interacts with itself through the emission of virtual photons that link to virtual electron-positron pairs. This process leads to the propagator Green’s function for the electron and is the starting point for including the simple electron in more complex particle interactions.
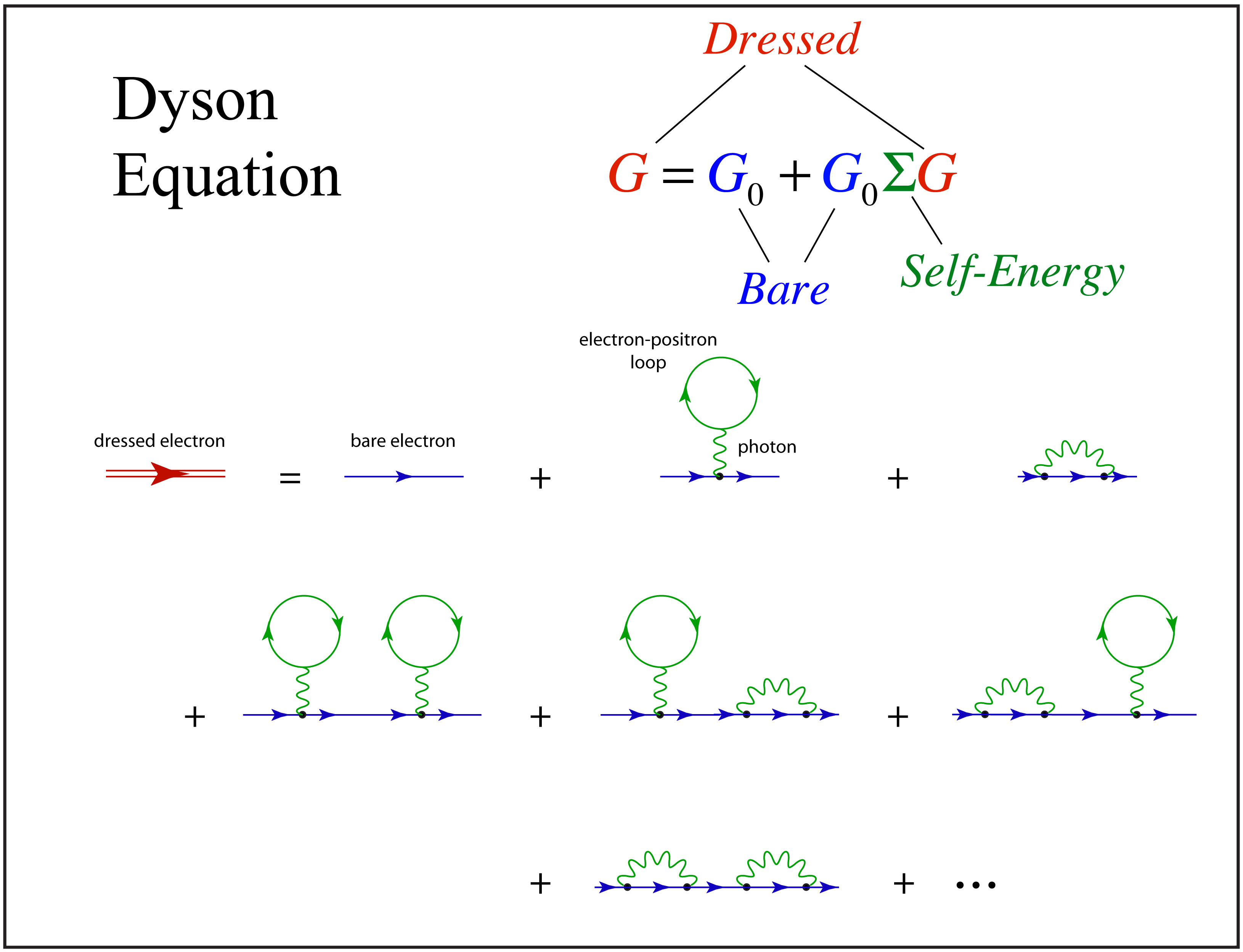
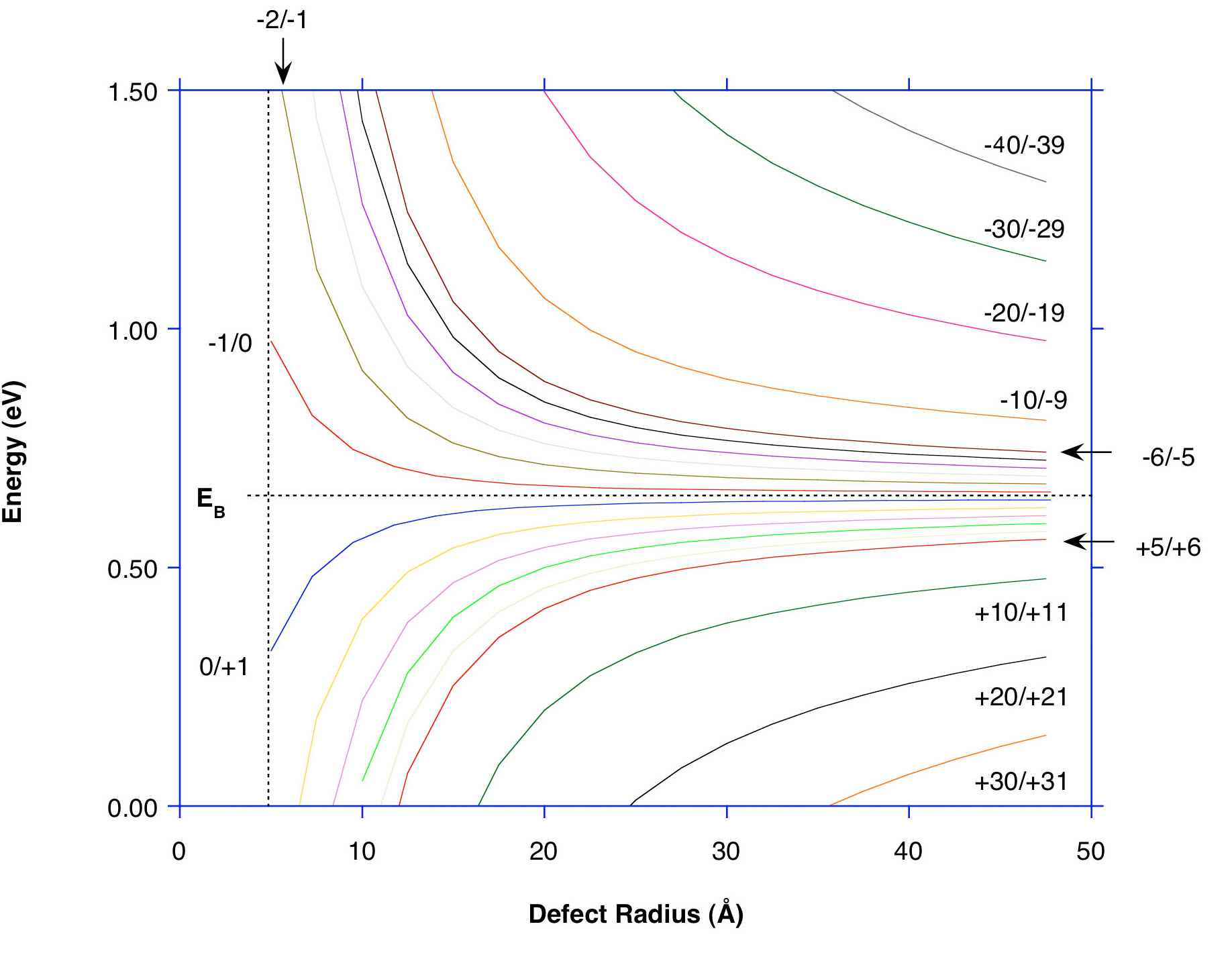
I had no feel for the use of the Dyson equation, barely limping through relativistic quantum mechanics, until a few years later when I was working at Lawrence Berkeley Lab with Mirek Hamera, a visiting scientist from Warwaw Poland who introduced me to the Haldane-Anderson model that applied to a project I was working on for my PhD. Using the theory, with Dyson’s equation at its heart, we were able to show that tightly bound electrons on transition-metal impurities in semiconductors acted as internal reference levels that allowed us to measure internal properties of semiconductors that had never been accessible before. A few years later, I used Dyson’s equation again when I was working on small precipitates of arsenic in the semiconductor GaAs, using the theory to describe an accordion-like ladder of electron states that can occur within the semiconductor bandgap when a nano-sphere takes on multiple charges [4].
I last saw Dyson when he gave the Hubert James Memorial Lecture at Purdue University in 1996. The title of his talk was “How the Dinosaurs Might Have Been Saved: Detection and Deflection of Earth-Impacting Bodies”. As always, his talk was wild and wide ranging, using the simplest possible physics to derive the most dire consequences of our continued existence on this planet.
[1] Dyson, F. J. (1949). “THE RADIATION THEORIES OF TOMONAGA, SCHWINGER, AND FEYNMAN.” Physical Review 75(3): 486-502.
[2] Feynman, R. P. (1949). “THE THEORY OF POSITRONS.” Physical Review 76(6): 749-759. Feynman, R. P. (1949). “SPACE-TIME APPROACH TO QUANTUM ELECTRODYNAMICS.” Physical Review 76(6): 769-789.
[3] Kaiser, D., K. Ito and K. Hall (2004). “Spreading the tools of theory: Feynman diagrams in the USA, Japan, and the Soviet Union.” Social Studies of Science 34(6): 879-922.
[4] Nolte, D. D. (1998). “Mesoscopic Point-like Defects in Semiconductors.” Phys. Rev. B58(12): pg. 7994