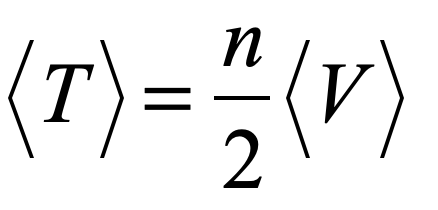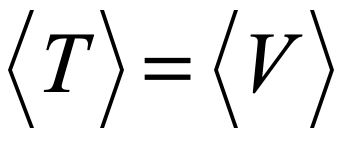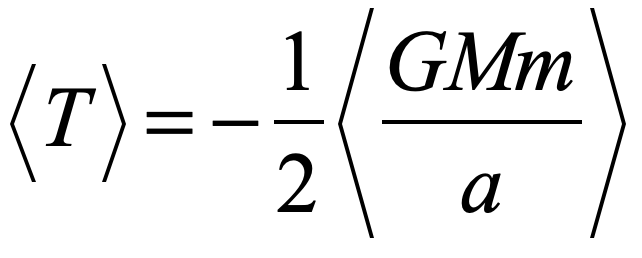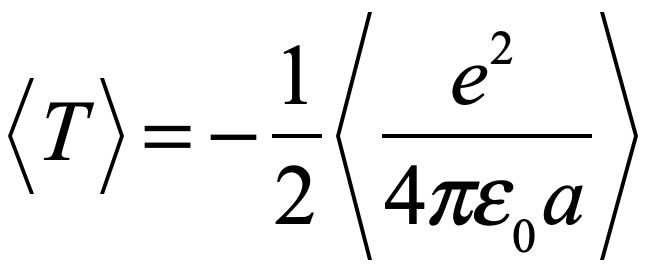The Rise of Wave Mechanics by Erwin Schrödinger

January 7, 2026 by David D. Nolte

100 Years of Quantum Physics: Schrödinger’s Wave Mechanics (1926)

History of Dynamics, Quantum Explorations
Einstein, Erwin Schrödinger, Hamiltonian Mechanics, History of Physics, Ideal Gas, philosophy, physics, Quantum Mechanics, quantum-physics, science, Wave Mechanics, Wave-Particle Duality

By the middle of 1925, a middle-aged Erwin Schrödinger was casting about, bogged down in mid career, looking for something significant to say about the rapidly accelerating field of quantum theory. He was known for his breadth of knowledge, and for his belief in his own creative genius [1], but a grand synthesis had so far eluded him.

Einsteinian Gas Theory

In the middle of the year, Schrödinger was deep analyzing two papers recently published by Einstein (Sept. 1924 and Feb. 1925) on the quantum properties of ideal gases where Einstein applied the new statistical theory of Bose to the counting of states in a volume of the gas [2]. One of the intriguing discoveries made by Einstein in those papers was a close analogy between the fluctuation of gas numbers and the interference of waves. He stated:

‘I believe that this is more than a mere analogy; de Broglie has shown in a very important work how a (scalar) wave field can be coordinated with a material particle or a system of material particles’

referring to de Broglie’s thesis work of 1924 that associated a wave-like property to mass. Einstein had been the first to attribute a wave-particle duality to the quantum phenomenon of black-body radiation, giving a lecture in Salzburg, Austria, in 1909 showing relationships between the particle-like and the wave-like properties of the radiation, and he found similar behavior in the properties of monatomic ideal gases, though his derivations were purely statistical.

Erwin Schrödinger photo — *Fig. 1 Erwin Schrödinger* (Source)

Schrödinger was suspicious of the “unnatural” way of counting states used by Einstein and Bose for the gas, and he sought a more “natural” way of explaining how the elements of phase space were filled. It struck him that, just as Planck’s black-body radiation spectrum could be derived by assuming discrete standing-wave modes for the electromagnetic radiation, then perhaps the behavior of ideal gases could be obtained using a similar approach. He and Einstein exchanged several letters about this idea as Schrödinger dug deeper into de Broglie’s theory.

The Zurich Seminar

At that time, Schrödinger was in the Chair of Theoretical Physics at the University of Zurich, holding the same chair that Einstein had held 15 years earlier. Following Einstein, the chair had been occupied by Max von Laue and then by Peter Debye who moved to the ETH in Zurich. Debye organized a joint seminar between the University and ETH that was a hot social gathering of physicists and physical chemists, discussing the latest developments in atomic and quantum science.

In November of 2025, Debye, who probably knew about the Einstein-Schrödinger discussion on de Broglie, asked Schrödinger to give a seminar on de Broglie’s theory to the group. A young Felix Bloch, who was a graduate student at that time, recalled hearing Debye say something like

“Schrödinger, you are not working right now on very important problems anyway. Why don’t you tell us sometime about that thesis of de Broglie, which seems to have attracted some attention?”[3]

Schrödinger gave the overview seminar in early December, showing how the Bohr-Sommerfeld quantization conditions could be explained as standing waves using de Broglie’s theory, but Bloch recalled Debye was unimpressed, saying that de Broglie’s way of talking was “childish” and that what was needed for a proper physics theory was a wave equation.

This exchange between Schrödinger and Debye was recalled only in later years, and there is debate about what exactly was said and what effect it had on Schrödinger. From Schrödinger’s letters to friends, it is clear that he was already well into his investigations of wavelike properties of matter when Debye asked him to give the seminar. Furthermore, he had already tried to construct wave packets using superpositions of phase waves propagating along Bohr-Sommerfeld elliptical orbits but had been led to ugly caustics when he tried to apply the packets to the hydrogen atom [4]. Therefore, although Debye was probably not the source of Schrödinger’s interest in de Broglie, it is possible that Debye’s quip about “childishness” may have spurred Schrödinger to find a wave equation subject to boundary conditions rather than working with packets following ray paths.

The Christmas Breakthrough

By this time, Christmas was approaching and Schrödinger arranged to take a vacation away from his family to the Swiss Alpine village of Arosa, and given his unconventional belief in the link between personal pleasure and genius, he did not go alone. There is no record of what transpired, and no record of which mistress was with him on this particular trip, nor how she spent her time while he worked on his theory, but two days after Christmas he wrote a letter to the physicist Willy Wien saying

“At the moment I am struggling with a new atomic theory. If only I knew more mathematics! I am very optimistic about this thing, and expect that, if only I can . . . solve it, it will be very beautiful.. . . I hope that I can soon report in a little more detailed and understandable way about the matter. At present I must learn a little mathematics in order to completely solve the vibration problem …”[5]

He had uncovered his first wave equation. When he returned to Zurich, he enlisted the help of his friend, the mathematician Hermann Weyl at the University in Zurich, and Schrödinger had his first eigenfrequencies for hydrogen. But they were wrong!

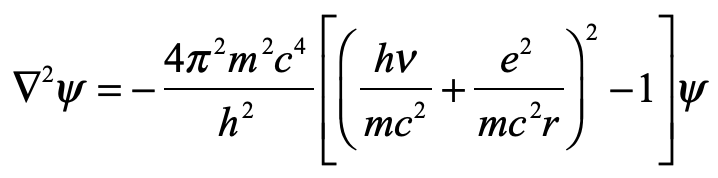
*Fig. 2 Schrödinger’s first wave equation was relativistic.*

The theory of de Broglie was fundamentally a relativistic theory, motivated by mapping the behavior of matter onto the behavior of light. Therefore, Schrödinger’s first attempt was also relativistic, equivalent to the Klein-Gordon equation. But there was no clear understanding of electron spin at that time, even though it had been established as a fundamental property of the electron. It was only several years later when Dirac correctly accounted for electron spin in a relativistic wave equation.

Dirac relativistic quantum wave equation — *Fig. 3 The full relativistic Dirac equation.*

The Schrödinger Wave Equation

Convinced that he was onto something big, and unwilling to fail, despite his failure to obtain correct values for hydrogen, Schrödinger went back to first principles, to the classical theory of Hamiltonian mechanics, identifying Hamilton’s characteristic function with the phase of an electron wave and deriving a non-relativistic equation using variational principles subject to boundary conditions. The eigenvalues of this new equation, when applied to hydrogen, matched the Bohr spectrum perfectly!

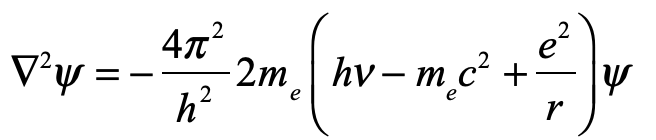
*Fig. 4. Schrödinger’s second wave equation was non-relativistic and correctly matched the Bohr energy levels of hydrogen.*

It had been only a few weeks since Schrödinger had given his previous seminar to the Zurich group, but in January he gave his update, probably given with some degree of satisfaction, having Debye in attendance, showing his now-famous wave equation and the agreement with experiment. Schrödinger wrote up his theory and results and submitted his paper on January 27, 1926, to Annalen der Physik [6].

*Fig. 5 Hydrogen quantum orbitals* (Source)

Schrödinger had been known, but not as a forefront thinker, despite what he believed about himself. Now he was a forefront thinker, vindicating his beliefs but not always on the right track. He continued his unconventional lifestyle, marginalizing him socially, and he resisted Max Born’s and Niels Bohr’s probabilistic interpretations of the meaning of his own quantum wavefunction, marginalizing him professionally. Yet his breakthrough gave him a platform, and his skeptical reactions to his colleague’s successes helped illuminate the nature of the new physics (“Schrödinger’s Cat” [7]) through the decades to follow.

Bibliography

A very large body of historical work exists on the discovery of the Schrödinger equation, partially fueled by the lack of first-person accounts on how he achieved it. There has been a lot of speculation and a lot of sleuthing to uncover his path of discovery. Several accounts differ mainly in the timing of when he derived his equations, although all agree on the sequence: that the relativistic equation preceded the non-relativistic one. Here is a small sampling of the literature:

• Hanle, P. A. (1977). “The Coming of Age of Erwin Schrödinger: His Quantum Statistics of Ideal Gases.” Archive for History of Exact Sciences, 17(2), 165–192. DOI: 10.1007/BF00328532.

• Hanle, P. A. (1979). “The Schrödinger‐Einstein correspondence and the sources of wave mechanics.” American Journal of Physics, 47(7), 644–648. DOI: 10.1119/1.11587.

• Mehra, Jagdish. “Erwin Schrödinger and the Rise of Wave Mechanics. II. The Creation of Wave Mechanics.” Foundations of Physics, vol. 17, no. 12, 1987, pp. 1141-1188.

• Renn, J. (2013). “Schrödinger and the Genesis of Wave Mechanics.” In W. L. Reiter & J. Yngvason (Eds.), Erwin Schrödinger – 50 Years After (pp. 9–36). Zurich: European Mathematical Society. DOI: 10.4171/121-1/2.

• Wessels, L. (1979). “Schrödinger’s Route to Wave Mechanics.” Studies in History and Philosophy of Science Part A, 10(4), 311–340.

Notes

[1] He led an unconventional lifestyle (some would say emotionally predatory) based on his belief in the personal origins of genius. Although this behavior presented significant social barriers to his career, he refused to abandon it.

[2] A. Enstein, ‘Quantentheorie des einatomigen idealen Gases’, Preuss. Ak. Wiss. Sitzb. (1924) pp. 261 – 267, and (1925), pp. 3-14.

[3] Quoted in Mehra, pg. 1150

[4] Mehra, pg. 1147

[5] Wessels, pg. 328

[6] Schrödinger, Erwin. “Quantisierung als Eigenwertproblem (Erste Mitteilung).” Annalen Der Physik, vol. 384, no. 4, 1926, pp. 361-376.

[7] Schrödinger, E. (1935). “Die gegenwärtige Situation in der Quantenmechanik.” Naturwissenschaften 23: 807–812, 823–828, 844–849. Schrödinger, E. (1980). “The Present Situation in Quantum Mechanics: A Translation of Schrödinger’s ‘Cat Paradox’ Paper.” Proceedings of the American Philosophical Society 124 (5): 323–338. (Translated by J. D. Trimmer).

Read more in Books by David Nolte at Oxford University Press

December 3, 2025December 30, 2025 by David D. Nolte

100 Years of Quantum Physics: Rise of the Matrix (1925)

Niels Bohr’s atom, by late 1925, was a series of kludges cobbled together into a Rube Goldberg type of construction. On the one hand, there was the Bohr-Sommerfeld quantization conditions that let Bohr’s originally circular orbits morph into ellipses like planets in the solar system. On the other hand, there was Pauli’s exclusion principle that partially explained the building up of electron orbits in many-electron atoms, but to many it seemed like an ad hoc rule.

The time was ripe for a new perspective. Enter the wunderkind, Werner Heisenberg.

Heisenberg’s Trajectory

Werner Heisenberg (1901 – 1976) was the golden boy—smart, dashing, ambitious. He excelled at everything he did and was a natural leader among his group of young friends. He entered the University of Munich in 1920 at the age of 19 to begin working towards his doctorate degree in mathematics, but he quickly became entranced with an advanced seminar course given by Arnold Sommerfeld (1868 – 1951) on quantum mechanics. His studies under Sommerfeld advanced quickly, and he was proficient enough to be “lent out” to the group of Max Born and David Hilbert at the University of Göttingen for the 1922-1923 semester when Sommerfeld was on sabbatical at the University of Wisconsin, Madison, in the United States. Born was impressed with the young student and promised him a post-doc position upon his graduation with a doctoral degree in theoretical physics the next year (when Heisenberg would be just 22 years old).

Unfortunately, his brilliantly ascending career ran headlong into “Willy” Wien who had won the Nobel Prize in 1911 for his displacement law of black body radiation. Wien was a hard-baked experimentalist who had little patience with the speculative flights of theoretical physics. Heisenberg, in contrast, had little patience with the mundane details of experimental science. The two were heading for an impasse.

The collision came during the oral examination for Heisenberg’s doctoral degree. Wien, determined to put Heisenberg in his place, opened with a difficult question about experimental methods. Heisenberg could not answer, so Wien asked a slightly less difficult but still detailed question that Heisenberg also could not answer. The examination went on like this until finally Wien asked Heisenberg to derive the resolving power of a simple microscope. Heisenberg was so flustered by this time that he could not do even that. Wien, in disgust, turned to Sommerfeld and pronounced a failing grade for Heisenberg. After Heisenberg stepped out of the room, the professors wrangled over the single committee grade that would need to be recorded. Sommerfeld’s top grade for Heisenberg’s mathematical performance and Wien’s bottom grade for his experimental performance led to the compromise grade of a “C” for the exam—the minimum grade sufficient to pass.

Heisenberg was mortified. Accustomed always to excelling and being lauded for his talents, Heisenberg left town that night, taking the late train to Göttingen where a surprised Born found him outside his office early the next morning—fully two months ahead of schedule. Heisenberg told him everything and asked if Born would still have him. After learning more about Wien’s “ambush”, Born assured Heisenberg that he still had a place for him.

Heisenberg was so successful at Göttingen, that when Born planned to spend a year sabbatical at MIT in the United States for the 1924-1925 semester, Heisenberg was “lent out” to Niels Bohr in Copenhagen. While there, Heisenberg, Bohr, Pauli and Kramers had intense discussions about the impending crisis in quantum theory. Bohr was fully aware of the precarious patches that made up the quantum theory of the many-electron atom, and the four physicists attempted to patch it yet again with a theoretical effort led by Kramers to try to reconcile optical transitions in the atomic spectra. But no one was satisfied, and the theory had serious internal inconsistencies, not the least of which was a need to sacrifice the sacrosanct principle of conservation of energy.

Through it all, Heisenberg was thrilled by his deep involvement in the most fundamental questions of physics of the day and was even more thrilled by his interactions with the great minds he found in Copenhagen. When he returned to Göttingen on April 27, 1925, the arguments and inconsistencies were ringing in his head, infecting the group at Göttingen with the challenging physics, especially Max Born and Pascual Jordan.

Little headway could be made, until Heisenberg had a serious attack of hay fever that sent him for respite on June 7 to the remote island of Helgoland in the North Sea far off of the coast from Bremerhaven. The trip cleared Heisenberg’s head—literally and figuratively—as he had time to come to grips with the core difficulties of quantum theory.

Trajectory’s End

The Mythology of Physics recounts the tale of when Heisenberg had his epiphany, watching from the beach as the sun rose over the sea. The repeated retelling has solidified the moment into revealed “truth”, but the origins are probably more prosaic. Strip a problem bare of all its superficial coverings and what remains must be the minimal set of what can be known. Yet to do so requires courage, for much of the superficial coverings are established dogma, embedded so deeply in the thought of the day that angry reactions must be expected.

Map of Heligoland, Germany — Fig. 1 Heligoland Germany. *(From Google Maps and Wikipedia)*

At some moment, Heisenberg realized that the superficial covering of atomic theory was the slavish devotion to the electron trajectory—to the Bohr-Sommerfeld electron orbits. Ever since Kepler, the mental image of masses in orbit around their force center had dominated physical theory. Quantum theory likewise was obsessed with images of trajectories—it persists to this day in the universal logo of atomic energy. Heisenberg now rejected this image as unknowable and hence not relevant for a successful theory. But if electron orbits were out, what was the minimal set of what can be known to be true? Heisenberg decided that it was simply the wavelengths and intensities of light absorbed and emitted by atoms. But what then? How do you create a theory constructed on transition energies and intensities alone? The epiphany was the answer—construct a dynamics by which the quantum system proceeds step-by-step, transition-by-transition, while retaining the sacrosanct energy conservation that had been discarded by Kramer’s unsuccessful theory.

The result, after returning to Göttingen, is Heisenberg’s paper, submitted July 29, 1925 to Zeitschrift für Physik titled Über quantentheoretische Umdeutung kinematischer und mechanischer Beziehungen (Over the quantum theoretical meaning of kinematic and mechanical relationships).

Heisenberg 1925 Over quantum theoretical meaning of kinematic and mechanical relationships — Fig. 2 The heading of Heisenberg’s 1925 Zeitschrift für Physik article. The abstract reads: “This work seeks to find fundamental principles for a quantum theoretical mechanics that is based exclusively on relationships among principal observable magnitudes.” [1]

Heisenberg begins with the fundamental energy relationship between the frequency of light and the energy difference in a transition

Heisenberg 1925 Zeitschrift fur Physik paper on transition energies — *Fig. 3 Dynamics emerges from the transitions among different energy states in the atom [1].*

His goal is to remove the electron orbit from the theory, yet positions cannot be removed entirely, so he takes the step of transforming position into a superposition of amplitudes with frequencies related to the optical transitions.

Heisenberg replacing the electron orbits with their Fourier coefficients based on transition frequencies. — *Fig. 4 Replace the electron orbits with their Fourier coefficients based on transition frequencies [1].*

Armed with the amplitude coefficients and the transition frequencies, he constructs sums of transitions that proceed step by step between initial and final states.

Heisenberg connecting initial and final states with series of steps that conserve energy. — *Fig. 5 Consider all the possible paths between initial and final states that obey energy conservation [1].*

After introducing the electric field, Heisenberg calculates the polarizability of the atom, the induced moment, using Kramer’s dispersion formula combined with his new superposition.

Heisenberg transition amplitude based on sums over possible energy steps — *Fig. 6 Transition amplitude between initial and final states based on a series of energy-conserving transition steps [1].*

Heisenberg applied his new theoretical approach to one-dimensional quantum systems, using as an explicit example the anharmonic oscillator, and it worked! Heisenberg had invented a new theoretical approach to quantum physics that relied only on transition frequencies and amplitudes—only what could be measured without any need to speculate on what types of motions electrons might be executing. Heisenberg published his new theory on his own, as sole author befitting his individual breakthrough. Yet it was done under the guidance of his supervisor Max Born, who recognized something within Heisenberg’s mathematics.

The Matrix

Heisenberg’s derivations involved numerous summations as amplitudes multiplied amplitudes in complicated sequences. The mathematical steps themselves were straightforward—just products and sums—but the numbers of permutations were daunting, and their sequential order mattered, requiring skill and care not to miss terms or to get minus signs wrong.

Yet Born recognized within Heisenberg’s mathematics the operations of matrix multiplication. The different permutations with sums of alternating signs were exactly what one obtained by taking determinants of matrices, and it was well known that the order of matrix multiplication mattered, where a*b ≠ b*a. With his assistant Pacual Jordan, the two reworked Heisenberg’s paper in the mathematical language of matrices, submitting their “mirror” paper to Zeitschrift on Sept. 27, 1925. Their title was prophetic: Towards Quantum Mechanics. This was the first time that the phrase “quantum mechanics” was used to encompass all of the widely varying aspects of quantum systems.

Born and Jordan 1925 Zur Quantenmechanik — *Fig. 7 The header for Born and Jordan’s reworking of Heisenberg’s paper into matrix mathematics [2].*

In the abstract, they state:

The approaches recently put forward by Heisenberg (initially for systems with one degree of freedom) are developed into a systematic theory of quantum mechanics. The mathematical tool is matrix calculus. After this is briefly outlined, the mechanical equations of motion are derived from a variational principle, and the proof is carried out that, on the basis of Heisenberg’s quantum condition, the energy theorem and Bohr’s frequency condition follow from the mechanical equations. Using the example of the anharmonic oscillator, the question of the uniqueness of the solution and the significance of the phases in the partial oscillations are discussed. The conclusion describes an attempt to incorporate the laws of the electromagnetic field into the new theory.

Born and Jordan begin by creating a matrix form for the Hamiltonian subject to Hamilton’s dynamical equations

Born Hamiltonian and Hamilton's equations — *Fig. 8 Defining the Hamiltonian with matrix operators [2].*

Armed with matrix quantities for position and momentum, Born and Jordan construct the commutator of p with q to arrive at one of the most fundamental quantum relationships: the non-zero difference in the permuted products related to Planck’s constant. This commutation relationship would become the foundation for many quantum theories to come.

Born 1925 matrix commutator — *Fig. 9 Page 871 of Born and Jordan’s 1925 Zeitschrift article that introduces the commutation relationship between p and q [2].*

As Heisenberg had done in his paper, Born and Jordan introduce the electric field of light to derive the dispersion of an atomic gas.

Max Born quantum transition amplitude from matrix elements — *Fig. 10 Expression for the dispersion of light in an atomic gas [2].*

The Born and Jordan paper appeared in the November issue of Zeitschrift für Physik, although a pre-print was picked up in England by Paul Dirac, who was working towards his doctoral degree under the mentorship of Ralph Fowler (1889 – 1944) at Cambridge. Dirac was deeply knowledgable in classical mechanics, and he recognized as soon as he saw it that the new quantum commutator was intimately connected to a quantity in classical mechanics known as a Poisson bracket. The Poisson bracket is part of Hamiltonian mechanics that defines how two variables, known as conjugate variables, are connected. For instance, the Poisson bracket of x with px is non-zero, meaning that these are conjugate variables, while the Poisson bracket of x with py is zero, meaning that these variables are fully independent. Conjugate variables are not “dependent” in an algebraic sense, but are linked through the structure of Hamilton’s equations—they are the “p’s and q’s” of phase space.

Dirac 1926 Proceedings of the Royal Society comparison of Poisson bracket to quantum commutator. — *Fig. 11 The Poisson bracket in Dirac’s paper submitted on Nov. 7, 1925 [3].*

Dirac submitted a paper on Nov. 7, 1925 to the Proceedings of the Royal Society of London where he showed that the Heisenberg commutator (a quantum quantity) directly proportional to the Poisson bracket (the classical quantity) with a proportionality factor that depended on Planck’s constant.

Dirac quantum commutation relationship — *Fig. 12 Dirac relating the quantum commutator to the classical Poisson (Jacobi) bracket [3].*

The Drei-Männer Quantum Mechanics Paper: Born, Heisenberg, and Jordan

Meanwhile, back in Göttingen, the three quantum physicists Born, Heisenberg and Jordan now combined forces to write a third foundational paper that established the full range of the new matrix mechanics. Heisenberg’s first paper had been the insight. Born and Jordan’s following paper had re-expressed Heistenberg’s formulas into matrix algebra. But both papers had used simple one-dimensional problems as test examples. Working together, they extended the new quantum mechanics to systems with many degrees of freedom.

Quantum Mechanics. Born, Heisenberg and Jordan three-man paper heading. — *Fig. 13 Header for the completed new theory on quantum mechanics by Born, Heisenberg and Jordan [4].*

With this paper, the matrix properties of dynamical variables are defined and used in their full form.

Quantum Mechanics. Born, Heisenberg and Jordan. View of a matrix. — *Fig. 14 An explicit form for a dynamical matrix in the “three-man” paper [4].*

With the theory out in the open, Pauli in Hamburg and Dirac at Cambridge used the new quantum mechanics to derive the transition energies of hydrogen, while Lucy Mensing and J. Robert Oppenheimer in Göttingen extended it to the spectra of more complicated molecules.

Open Issues

Heisenberg’s matrix mechanics might have exclusively taken hold of the quantum theory community and we would all be using matrices today to perform all our calculations. But within one month of the success of matrix mechanics, an alternative quantum theory would be proposed by Erwin Schrödinger based on waves, a theory that came to be called wave mechanics. There was a minor battle fought over matrix mechanics versus wave mechanics, but in the end, Bohr compromised with his complementarity principle, allowing each to stand as equivalent viewpoints of quantum phenomena (but more about Schrödinger and his waves in my next Blog).

References

[1] Heisenberg, W. (1925). “Über quantentheoretische Umdeutung kinematischer und mechanischer Beziehungen”. Zeitschrift für Physik, 33(1), 879–893.

[2] Born, M., & Jordan, P. (1925). “Zur Quantenmechanik”. Zeitschrift für Physik, 34(1), 858–888.

[3] Dirac, P. A. M. (1925). The fundamental equations of quantum mechanics. Proceedings of the Royal Society of London. Series A, Containing Papers of a Mathematical and Physical Character, 109(752), 642–653

[4] Born, M., W. Heisenberg and P. Jordan (1926). “Quantum mechanics II.” Zeitschrift Fur Physik, 35, (8/9): 557–615.

[5] Dirac, P. A. M. (1926). “Quantum mechanics and a preliminary investigation of the hydrogen atom.” Proceedings of the Royal Society of London Series A, 110(755): 561–79.

[6] Pauli, W. (1926). “The hydrogen spectrum from the view point of the new quantal mechanics.” Zeitschrift Fur Physik, 36(5): 336–63.

[7] Mensing, L. (1926). “Die Rotations-Schwingungsbanden nach der Quantenmechanik”. Zeitschrift für Physik, 36(11), 814–823.

[8] Born, M., & Oppenheimer, J. R. (1927). “Zur Quantentheorie der Molekeln”. Annalen der Physik, 389(20), 457–484.

December 11, 2024September 5, 2025 by David D. Nolte

100 Years of Quantum Physics: Pauli’s Exclusion Principle (1924)

One hundred years ago this month, in December 1924, Wolfgang Pauli submitted a paper to Zeitschrift für Physik that provided the final piece of the puzzle that connected Bohr’s model of the atom to the structure of the periodic table. In the process, he introduced a new quantum number into physics that governs how matter as extreme as neutron stars, or as perfect as superfluid helium, organizes itself.

He was led to this crucial insight, not by his superior understanding of quantum physics, which he was grappling with as much as Bohr and Born and Sommerfeld were at that time, but through his superior understanding of relativistic physics that convinced him that the magnetism of atoms in magnetic fields could not be explained through the orbital motion of electrons alone.

Encyclopedia Article on Relativity

Bored with the topics he was being taught in high school in Vienna, Pauli was already reading Einstein on relativity and Emil Jordan on functional analysis before he arrived at the university in Munich to begin studying with Arnold Sommerfeld. Pauli was still merely a student when Felix Klein approached Sommerfeld to write an article on relativity theory for his Encyclopedia of Mathematical Sciences. Sommerfeld by that time was thoroughly impressed with Pauli’s command of the subject and suggested that he write the article.

PauliRelativity Download

Pauli’s encyclopedia article on relativity expanded to 250 pages and was published in Klein’s fifth volume in 1921 when Pauli was only 21 years old—just 5 years after Einstein had published his definitive work himself! Pauli’s article is still considered today one of the clearest explanations of both special and general relativity.

Pauli’s approach established the methodical use of metric space concepts that is still used today when teaching introductory courses on the topic. This contrasts with articles written only a few years earlier that seem archaic by comparison—even Einstein’s paper itself. As I recently read through his article, I was struck by how similar it is to what I teach from my textbook on modern dynamics to my class at Purdue University for junior physics majors.

Anomalous Zeeman Effect

In 1922, Pauli completed his thesis on the properties of water molecules and began studying a phenomenon known as the anomalous Zeeman effect. The Zeeman effect is the splitting of optical transitions in atoms under magnetic fields. The electron orbital motion couples with the magnetic field through a semi-classical interaction between the magnetic moment of the orbital and the applied magnetic field, producing a contribution to the energy of the electron that is observed when it absorbs or emits light.

The Bohr model of the atom had already concluded that the angular momentum of electron orbitals was quantized into integer units. Furthermore, the Stern-Gerlach experiment of 1922 had shown that the projection of these angular momentum states onto the direction of the magnetic field was also quantized. This was known at the time as “space quantization”. Therefore, in the Zeeman effect, the quantized angular momentum created quantized energy interactions with the magnetic field, producing the splittings in the optical transitions.

File:Breit-rabi-Zeeman-en.svg — Fig. 2 The magnetic Zeeman splitting of Rb-87 from the weak field to the strong-field (Pachen-Back) effect

So far so good. But then comes the problem with the anomalous Zeeman effect.

In the Bohr model, all angular momenta have integer values. But in the anomalous Zeeman effect, the splittings could only be explained with half integers. For instance, if total angular momentum were equal to one-half, then in a magnetic field it would produce a “doublet” with +1/2 and -1/2 space quantization. An integer like L = 1 would produce a triplet with +1, 0, and -1 space quantization. Although doublets of the anomalous Zeeman effect were often observed, half-integers were unheard of (so far) in the quantum numbers of early quantum physics.

But half integers were not the only problem with “2”s in the atoms and elements. There was also the problem of the periodic table. It, too, seemed to be constructed out of “2”s, multiplying a sequence of the difference of squares.

The Difference of Squares

The difference of squares has a long history in physics stretching all the way back to Galileo Galilei who performed experiments around 1605 on the physics of falling bodies. He noted that the distance traveled in successive time intervals varied as the difference 1² – 0² = 1, then 2²-1² = 3, then 3²-2² = 5, then 4²-3² = 7 and so on. In other words, the distances traveled in each successive time interval varied as the odd integers. Galileo, ever the astute student of physics, recognized that the distance traveled by an accelerating body in a time t varied as the square of time t². Today, after Newton, we know that this is simply the dependence of distance for an accelerating body on the square of time s = (1/2)gt².

By early 1924 there was another law of the difference of squares. But this time the physics was buried deep inside the new science of the elements, put on graphic display through the periodic table.

The periodic table is constructed on the difference of squares. First there is 2 for hydrogen and helium. Then another 2 for lithium and beryllium, followed by 6 for B, C, N, O, F and Ne to make a total of 8. After that there is another 8 plus 10 for the sequence of Sc, Ti, V, Cr, Mn, Fe, Co, Ni, Cu and Zn to make a total of 18. The sequence of 2-8-18 is 2•1² = 2, 2•2² = 8, 2•3² = 18 for the sequence 2n².

Why the periodic table should be constructed out of the number 2 times the square of the principal quantum number n was a complete mystery. Sommerfeld went so far as to call the number sequence of the periodic table a “cabalistic” rule.

The Bohr Model for Many Electrons

It is easy to picture how confusing this all was to Bohr and Born and others at the time. From Bohr’s theory of the hydrogen atom, it was clear that there were different energy levels associated with the principal quantum number n, and that this was related directly to angular momentum through the motion of the electrons in the Bohr orbitals.

But as the periodic table is built up from H to He and then to Li and Be and B, adding in successive additional electrons, one of the simplest questions was why the electrons did not all reside on the lowest energy level? But even if that question could not be answered, there was the question of why after He the elements Li and Be behaved differently than B, N, O and F, leading to the noble gas Ne. From normal Zeeman spectroscopy as well as x-ray transitions, it was clear that the noble gases behaved as the core of succeeding elements, like He for Li and Be and Ne for Na and Mg.

To grapple with all of this, Bohr had devised a “building up” rule for how electrons were “filling” the different energy levels as each new electron of the next element was considered. The noble-gas core played a key role in this model, and the core was also assumed to be contributing to both the normal Zeeman effect as well as the anomalous Zeeman effect with its mysterious half-integer angular momenta.

But frankly, this core model was a mess, with ad hoc rules on how the additional electrons were filling the energy levels and how they were contributing to the total angular momentum.

This was the state of the problem when Pauli, with his exceptional understanding of special relativity, began to dig deep into the problem. Since the Zeeman splittings were caused by the orbital motion of the electrons, the strongly bound electrons in high-Z atoms would be moving at speeds near the speed of light. Pauli therefore calculated what the systematic effects would be on the Zeeman splittings as the Z of the atoms got larger and the relativistic effects got stronger.

He calculated this effect to high precision, and then waited for Landé to make the measurements. When Landé finally got back to him, it was to say that there was absolutely no relativistic corrections for Thallium (Z = 90). The splitting remained simply fixed by the Bohr magneton value with no relativistic effects.

Pauli had no choice but to reject the existing core model of angular momentum and to ascribe the Zeeman effects to the outer valence electron. But this was just the beginning.

Pauli’s Breakthrough

https://onionesquereality.wordpress.com/wp-content/uploads/2012/07/wolfgang-pauli.jpg — Fig. 5 Wolfgang Pauli [Image]

By November of 1924 Pauli had concluded, in a letter to Landé

“In a puzzling, non-mechanical way, the valence electron manages to run about in two states with the same k but with different angular momenta.”

And in December of 1924 he submitted his work on the relativistic effects (or lack thereof) to Zeitschrift für Physik,

“From this viewpoint the doublet structure of the alkali spectra as well as the failure of Larmor’s theorem arise through a specific, classically non-describable sort of Zweideutigkeit (two-foldness) of the quantum-theoretical properties of the valence electron. (Pauli, 1925a, pg. 385)

Around this time, he read a paper by Edmund Stoner in the Philosophical Magazine of London published in October of 1924. Stoner’s insight was a connection between the number of states observed in a magnetic field and the number of states filled in the successive positions of elements in the periodic table. Stoner’s insight led naturally to the 2-8-18 sequence for the table, although he was still thinking in terms of the quantum numbers of the core model of the atoms.

This is when Pauli put 2 plus 2 together: He realized that the states of the atom could be indexed by a set of 4 quantum numbers: n-the principal quantum number, k1-the angular momentum, m1-the space quantization number, and a new fourth quantum number m2 that he introduced but that had, as yet, no mechanistic explanation. With these four quantum numbers enumerated, he then made the major step:

It should be forbidden that more than one electron, having the same equivalent quantum numbers, can be in the same state. When an electron takes on a set of values for the four quantum numbers, then that state is occupied.

This is the Exclusion Principle: No two electrons can have the same set of quantum numbers. Or equivalently, no electron state can be occupied by two electrons.

Fig. 6 Level filling for Krypton using the Pauli Exclusion Principle

Today, we know that Pauli’s Zweideutigkeit is electron spin, a concept first put forward in 1925 by the American physicist Ralph Kronig and later that year by George Uhlenbeck and Samuel Goudsmit.

The “Famous” Pauli Exclusion Paper Download

And Pauli’s Exclusion Principle is a consequence of the antisymmetry of electron wavefunctions first described by Paul Dirac in 1926 after the introduction of wavefunctions into quantum theory by Erwin Schrödinger earlier that year.

Timeline:

1845 – Faraday effect (rotation of light polarization in a magnetic field)

1896 – Zeeman effect (splitting of optical transition in a magnetic field)

1897 – Anomalous Zeeman effect (half-integer splittings)

1902 – Lorentz and Zeeman awarded Nobel prize (for electron theory)

1921 – Paschen-Back effect (strong-field Zeeman effect)

1922 – Stern-Gerlach (space quantization)

1924 – de Broglie matter waves

1924 – Bose statistics of photons

1924 – Stoner (conservation of number of states)

1924 – Pauli Exclusion Principle

References:

E. C. Stoner (Philosophical Magazine, 48 [1924], 719) Issue 286 October 1924

M. Jammer, The conceptual development of quantum mechanics (Los Angeles, Calif.: Tomash Publishers, Woodbury, N.Y. : American Institute of Physics, 1989).

M. Massimi, Pauli’s exclusion principle: The origin and validation of a scientific principle (Cambridge University Press, 2005).

Pauli, W. Über den Einfluß der Geschwindigkeitsabhängigkeit der Elektronenmasse auf den Zeemaneffekt. Z. Physik 31, 373–385 (1925). https://doi.org/10.1007/BF02980592

Pauli, W. (1925). “Über den Zusammenhang des Abschlusses der Elektronengruppen im Atom mit der Komplexstruktur der Spektren”. Zeitschrift für Physik. 31 (1): 765–783

Read more in Books by David Nolte at Oxford University Press

September 25, 2024September 5, 2025 by David D. Nolte

Edward Purcell: From Radiation to Resonance

As the days of winter darkened in 1945, several young physicists huddled in the basement of Harvard’s Research Laboratory of Physics, nursing a high field magnet to keep it from overheating and dumping its field. They were working with bootstrapped equipment—begged, borrowed or “stolen” from various labs across the Harvard campus. The physicist leading the experiment, Edward Mills Purcell, didn’t even work at Harvard—he was still on the payroll of the Radiation Laboratory at MIT, winding down from its war effort on radar research for the military in WWII, so the Harvard experiment was being done on nights and weekends.

Just before Christmas, 1945, as college students were fleeing campus for the first holiday in years without war, the signal generator, borrowed from a psychology lab, launched an electromagnetic pulse into simple paraffin—and disappeared! It had been absorbed by the nuclear spins of the copious number of hydrogen nuclei (protons) in the wax.

The experiment was simple, unfunded, bootstrapped—and it launched a new field of physics that ultimately led to magnetic resonance imaging (MRI) that is now the workhorse of 3D medical imaging.

This is the story, in Purcell’s own words, of how he came to the discovery of nuclear magnetic resonance in solids, for which he was awarded the Nobel Prize in Physics in 1952.

Early Days

Edward Mills Purcell (1912 – 1997) was born in a small town in Illinois, the son of a telephone businessman, and some of his earliest memories were of rummaging around in piles of telephone equipment—wires and transformers and capacitors. He especially like the generators:

“You could always get plenty of the bell-ringing generators that were in the old telephones, which consisted of a series of horseshoe magnets making the stator field and an armature that was wound with what must have been a mile of number 39 wire or something like that… These made good shocking machines if nothing else.”

His science education in the small town was modest, mostly chemistry, but he had a physics teacher, a rare woman at that time, who was open to searching minds. When she told the students that you couldn’t pull yourself up using a single pulley, Purcell disagreed and got together with a friend:

“So we went into the barn after school and rigged this thing up with a seat and hooked the spring scales to the upgoing rope and then pulled on the downcoming rope.”

The experiment worked, of course, with the scale reading half the weight of the boy. When they rushed back to tell the physics teacher, she accepted their results immediately—demonstration trumped mere thought, and Purcell had just done his first physics experiment.

However, physics was not a profession in the early 1920’s.

“In the ’20s the idea of chemistry as a science was extremely well publicized and popular, so the young scientist of shall we say 1928 — you’d think of him as a chemist holding up his test tube and sighting through it or something…there was no idea of what it would mean to be a physicist.

The name Steinmetz was more familiar and exciting than the name Einstein, because Steinmetz was the famous electrical engineer at General Electric and was this hunchback with a cigar who was said to know the four-place logarithm table by heart.”

Purdue University and Prof. Lark-Horowitz

Purcell entered Purdue University in the Fall of 1929. The University had only 4500 students who paid $50 a year to attend. He chose a major in electrical engineering, because

“Being a physicist…I don’t remember considering that at that time as something you could be…you couldn’t major in physics. You see, Purdue had electrical, civil, mechanical and chemical engineering. It had something called the School of Science, and you could graduate, having majored in science.”

But he was drawn to physics. The Physics Department at Purdue was going through a Renaissance under the leadership of its new department head Prof. Lark-Horovitz

“His [Lark-Horovitz] coming to Purdue was really quite important for American physics in many ways… It was he who subsequently over the years brought many important and productive European physicists to this country; they came to Purdue, passed through. And he began teaching; he began having graduate students and teaching really modern physics as of 1930, in his classes.”

Purcell attended Purdue during the early years of the depression when some students didn’t have enough money to find a home:

“People were also living down there in the cellar, sleeping on cots in the research rooms, because it was the Depression and some of the graduate students had nowhere else to live. I’d come in in the morning and find them shaving.”

Lark-Horovitz was a demanding department chair, but he was bringing the department out of the dark ages and into the modern research world.

“Lark-Horovitz ran the physics department on the European style: a pyramid with the professor at the top and everybody down below taking orders and doing what the professor thought ought to be done. This made working for him rather difficult. I was insulated by one layer from that because it was people like Yearian, for whom I was working, who had to deal with the Lark. “

Hubert Yearian had built a 20-kilovolt electron diffraction camera, a Debye-Scherrer transmission camera, just a few years after Davisson and Germer had performed the Nobel-prize winning experiment at Bell Labs that proved the wavelike nature of electrons. Purcell helped Yearian build his own diffraction system, and recalled:

“When I turned on the light in the dark room, I had Debye-Scherrer rings on it from electron diffraction — and that was only five years after electron diffraction had been discovered. So it really was right in the forefront. And as just an undergraduate, to be able to do that at that time was fantastic.”

Purcell graduated from Purdue in 1933 and from contacts through Lark-Horovitz he was able to spend a year in the physics department at Karlsruhe in Germany. He returned to the US in 1934 to enter graduate scool in physics at Harvard, working under Kenneth Bainbridge. His thesis topic was a bit of a bust, a dusty old problem in classical electrostatics that was a topic far older than the electron diffraction he worked on at Purdue. But it was enough to get him his degree in 1938, and he stayed on at Harvard as a faculty instructor until the war broke out.

Radiation Laboratory, MIT

In the Fall at the end of 1940 the Radiation Lab at MIT was launched and began vacuuming up all the unattached physicists in the United States, and Purcell was one of them. The radiation lab also vacuumed up some of the top physicists in the country, like Isidor Rabi from Columbia, to supervise the growing army of scientists that were committed to the war effort—even before the US was in the war.

“Our mission was to make a radar for a British night fighter using 10-centimeter magnetron that had been discovered at Birmingham.”

This research turned Purcell and his cohort into experts in radio-frequency electronics and measurement. He worked closely with Rabi (Nobel Prize 1944) and Norman Ramsey (Nobel Prize 1989) and Jerrold Zacharias, who were in the midst of measuring resonances in molecular beams. The names at the Rad Lab was like reading a Who’s Who of physics at that time:

“And then there was the theoretical group, which was also under Rabi. Most of their theory was concerned with electromagnetic fields and signal to noise, things of that sort. George Uhlenbeck was in charge of it for quite a long time, and Bethe was in it for a while; Schwinger was in it; Frank Carlson; David Saxon, now president of the University of California; Goudsmit also.”

Nuclear Magnetic Resonance

The research by Rabi had established the physics of resonances in molecular beams, but there were serious doubts that such phenomena could exist in solids. This became one of the Holy Grails of physics, with only a few physicists across the country with the skill and understanding to make a try to observe it in the solid state.

Many of the physicists at the Rad Lab were wondering what they should do next, after the war was over.

“Came the end of the war and we were all thinking about what shall we do when we go back and start doing physics. In the course of knocking around with these people, I had learned enough about what they had done in molecular beams to begin thinking about what can we do in the way of resonance with what we’ve learned. And it was out of that kind of talk that I was struck with the idea for what turned into nuclear magnetic resonance.”

“Well, that’s how NMR started, with that idea which, as I say, I can trace back to all those indirect influences of talking with Rabi, Ramsey and Zacharias, thinking about what we should do next.

“We actually did the first NMR experiment here [Harvard], not at MIT. But I wasn’t officially back. In fact, I went around MIT trying to borrow a magnet from somebody, a big magnet, get access to a big magnet so we could try it there and I didn’t have any luck. So I came back and talked to Curry Street, and he invited us to use his big old cosmic ray magnet which was out in the shed. So I didn’t ask anybody else’s permission. I came back and got the shop to make us some new pole pieces, and we borrowed some stuff here and there. We borrowed our signal generator from the Psycho Acoustic Lab that Smitty Stevens had. I don’t know that it ever got back to him. And some of the apparatus was made in the Radiation Lab shops. Bob Pound got the cavity made down there. They didn’t have much to do — things were kind of closing up — and so we bootlegged a cavity down there. And we did the experiment right here on nights and week-ends.

This was in December, 1945.

“Our first experiment was done on paraffin, which I bought up the street at the First National store between here and our house. For paraffin we thought we might have to deal with a relaxation time as long as several hours, and we were prepared to detect it with a signal which was sufficiently weak so that we would not upset the spin temperature while applying the r-f field. And, in fact, in the final time when the experiment was successful, I had been over here all night … nursing the magnet generator along so as to keep the field on for many hours, that being in our view a possible prerequisite for seeing the resonances. Now, it turned out later that in paraffin the relaxation time is actually 10^-4 seconds. So I had the magnet on exactly 10⁸ times longer than necessary!

The experiment was completed just before Christmas, 1945.

E. M. Purcell, H. C. Torrey, and R. V. Pound, “RESONANCE ABSORPTION BY NUCLEAR MAGNETIC MOMENTS IN A SOLID,” Physical Review 69, 37-38 (1946).

“But the thing that we did not understand, and it gradually dawned on us later, was really the basic message in the paper that was part of Bloembergen’s thesis … came to be known as BPP (Bloembergen, Purcell and Pound). [This] was the important, dominant role of molecular motion in nuclear spin relaxation, and also its role in line narrowing. So that after that was cleared up, then one understood the physics of spin relaxation and understood why we were getting lines that were really very narrow.”

Diagram of the microwave cavity filled with paraffin.

This was the discovery of nuclear magnetic resonance (NMR) for which Purcell shared the 1952 Nobel Prize in physics with Felix Bloch.

David D. Nolte is the Edward M. Purcell Distinguished Professor of Physics and Astronomy, Purdue University. Sept. 25, 2024

References and Notes

• The quotes from EM Purcell are from the “Living Histories” interview in 1977 by the AIP.

• K. Lark-Horovitz, J. D. Howe, and E. M. Purcell, “A new method of making extremely thin films,” Review of Scientific Instruments 6, 401-403 (1935).

• E. M. Purcell, H. C. Torrey, and R. V. Pound, “RESONANCE ABSORPTION BY NUCLEAR MAGNETIC MOMENTS IN A SOLID,” Physical Review 69, 37-38 (1946).

• National Academy of Sciences Biographies: Edward Mills Purcell

July 24, 2024September 5, 2025 by David D. Nolte

The Vital Virial of Rudolph Clausius: From Stat Mech to Quantum Mech

I often joke with my students in class that the reason I went into physics is because I have a bad memory. In biology you need to memorize a thousand things, but in physics you only need to memorize 10 things … and you derive everything else!

Of course, the first question they ask me is “What are those 10 things?”.

That’s a hard question to answer, and every physics professor probably has a different set of 10 things. Obviously, energy conservation would be first on the list, followed by other conservation laws for various types of momentum. Inverse-square laws probably come next. But then what? What do you need to memorize to be most useful when you are working out physics problems on the back of an envelope, when your phone is dead, and you have no access to your laptop or books?

One of my favorites is the Virial Theorem because it rears its head over and over again, whether you are working on problems in statistical mechanics, orbital mechanics or quantum mechanics.

The Virial Theorem

The Virial Theorem makes a simple statement about the balance between kinetic energy and potential energy (in a conservative mechanical system). It summarizes in a single form many different-looking special cases we learn about in physics. For instance, everyone learns early in their first mechanics course that the average kinetic energy <T> of a mass on a spring is equal to the average potential energy <V>. But this seems different than the problem of a circular orbit in gravitation or electrostatics where the average kinetic energy is equal to half the average potential energy, but with the opposite sign.

Yet there is a unity to these two—it is the Virial Theorem:

for cases where the potential energy V has power law dependence V ≈ rⁿ. The harmonic oscillator has n = 2, leading to the well-known equality between average kinetic and potential energy as

The inverse square force law has a potential that varies with n = -1, leading to the flip in sign. For instance, for a circular orbit in gravitation, it looks like

and in electrostatics it looks like

where a is the radius of the orbit.

Yet orbital mechanics is hardly the only place where the Virial Theorem pops up. It began its life with statistical mechanics.

Rudolph Clausius and his Virial Theorem

The pantheon of physics is a somewhat exclusive club. It lets in the likes of Galileo, Lagrange, Maxwell, Boltzmann, Einstein, Feynman and Hawking, but it excludes many worthy candidates, like Gilbert, Stevin, Maupertuis, du Chatelet, Arago, Clausius, Heaviside and Meitner all of whom had an outsized influence on the history of physics, but who often do not get their due. Of this later group, Rudolph Clausius stands above the others because he was an inventor of whole new worlds and whole new terminologies that permeate physics today.

Within the German Confederation dominated by Prussia in the mid 1800’s, Clausius was among the first wave of the “modern” physicists who emerged from new or reorganized German universities that integrated mathematics with practical topics. Carl Neumann at Königsberg, Carl Gauss and Max Weber at Göttingen, and Hermann von Helmholtz at Berlin were transforming physics from a science focused on pure mechanics and astronomy to one focused on materials and their associated phenomena, applying mathematics to these practical problems.

Clausius was educated at Berlin under Heinrich Gustav Magnus beginning in 1840, and he completed his doctorate at the University of Halle in 1847. His doctoral thesis on light scattering in the atmosphere represented an early attempt at treating statistical fluctuations. Though his initial approach was naïve, it helped orient Clausius to physics problems of statistical ensembles and especially to gases. The sophistication of his physics matured rapidly and already in 1850 he published his famous paper Über die bewegende Kraft der Wärme, und die Gesetze, welche sich daraus für die Wärmelehre selbst ableiten lassen (About the moving power of heat and the laws that can be derived from it for the theory of heat itself).

This was the fundamental paper that overturned the archaic theory of caloric, which had assumed that heat was a form of conserved quantity. Clausius proved that this was not true, and he introduced what are today called the first and second laws of thermodynamics. This early paper was one in which he was still striving to simplify thermodynamics, and his second law was mostly a qualitative statement that heat flows from higher temperatures to lower. He refined the second law four years later in 1854 with Über eine veranderte Form des zweiten Hauptsatzes der mechanischen Wärmetheorie (On a modified form of the second law of the mechanical theory of heat). He gave his concept the name Entropy in 1865 from the Greek word τροπη (transformation or change) with a prefix similar to Energy.

Clausius was one of the first to consider the kinetic theory of heat where heat was understood as the average kinetic energy of the atoms or molecules that comprised the gas. He published his seminal work on the topic in 1857 expanding on earlier work by Augustus Krönig. Maxwell, in turn, expanded on Clausius in 1860 by introducing probability distributions. By 1870, Clausius was fully immersed in the kinetic theory as he was searching for mechanical proofs of the second law of thermodynamics. Along the way, he discovered a quantity based on action-reaction pairs of forces that was related to the kinetic energy.

At that time, kinetic energy was often called vis viva, meaning “living force”. The singular of force (vis) had a plural (virias), so Clausius—always happy to coin new words—called the action-reaction pairs of forces the virial, and hence he proved the Virial Theorem.

The argument is relatively simple. Consider the action of a single molecule of the gas subject to a force F that is applied reciprocally from another molecule. Also, for simplicity consider only a single direction in the gas. The change of the action over time is given by the derivative

The average over all action-reaction pairs is

but by the reciprocal nature of action-reaction pairs, the left-hand side balances exactly to zero, giving

This expression is expanded to include the other directions and to all N bodies to yield the Virial Theorem

where the sum is over all molecules in the gas, and Clausius called the term on the right the Virial.

An important special case is when the force law derives from a power law

Then the Virial Theorem becomes (again in just one dimension)

This is often the most useful form of the theorem. For a spring force, it leads to <T> = <V>. For gravitational or electrostatic orbits it is <T> = -1/2<V>.

The Virial in Astrophysics

Clausius originally developed the Virial Theorem for the kinetic theory of gases, but it has applications that go far beyond. It is already useful for simple orbital systems like masses interacting through central forces, and these can be scaled up to N-body systems like star clusters or galaxies.

Star clusters are groups of hundreds or thousands of stars that are gravitationally bound. Such a cluster may begin in a highly non-equilibrium configuration, but the mutual interactions among the stars causes a relaxation to an equilibrium configuration of positions and velocities. This process is known as Virialization. The time scale for virializaiton depends on the number of stars and on the initial configuration, such as whether there is a net angular momentum in the cluster.

A gravitational simulation of 700 stars is shown in Fig. 2. The stars are distributed uniformly with zero velocities. The cluster collapses under gravitational attraction, rebounds and approaches a steady state. The Virial Theorem applies at long times. The simulation assumed all motion was in the plane, and a regularization term was added to the gravitational potential to keep forces bounded.

Simulation of the virial theorem for a star cluster with kinetic and potential energy graphs — Fig. 2 A numerical example of the Virial Theorem for a star cluster of 700 stars beginning in a uniform initial state, collapsing under gravitational attraction, rebounding and then approaching a steady state. The kinetic energy and the potential energy of the system satisfy the Virial Theorem at long times.

The Virial in Quantum Physics

Quantum theory holds strong analogs to classical mechanics. For instance, the quantum commutation relations have strong similarities to Poisson Brackets. Similarly, the Virial in classical physics has a direct quantum analog.

Begin with the commutator between the Hamiltonian H and the action composed as the product of the position operator and the momentum operator X_nP_n

Expand the two commutators on the right to give

Now recognize that the commutator with the Hamiltonian is Ehrenfest’s Theorem on the time dependence of the operators

which equals zero when the system become stationary or steady state. All that remains is to take the expectation value of the equation (which can include many-body interactions as well)

which is the quantum form of the Virital Theorem which is identical to the classical form when the expectation value is replaced by the ensemble average.

For the hydrogen atom this is

for principal quantum number n and Bohr radius a_B. The quantum energy levels of the hydrogen atom are

By David D. Nolte, July 24, 2024

References

“Ueber die bewegende Kraft der Warme and die Gesetze welche sich daraus für die Warmelehre selbst ableiten lassen,” in Annalen der Physik, 79 (1850), 368–397, 500–524.

Über eine veranderte Form des zweiten Hauptsatzes der mechanischen Wärmetheorie, Annalen der Physik, 93 (1854), 481–506.

Ueber die Art der Bewegung, welche wir Warmenennen, Annalen der Physik, 100 (1857), 497–507.

Clausius, RJE (1870). “On a Mechanical Theorem Applicable to Heat”. Philosophical Magazine. Series 4. 40 (265): 122–127.

Matlab Code

function [y0,KE,Upoten,TotE] = Nbody(N,L)   %500, 100, 0

A = -1;        % Grav factor
eps = 1;        % 0.1
K = 0.00001;    %0.000025

format compact

mov_flag = 1;
if mov_flag == 1
    moviename = 'DrawNMovie';
    aviobj = VideoWriter(moviename,'MPEG-4');
    aviobj.FrameRate = 10;
    open(aviobj);
end

hh = colormap(jet);
%hh = colormap(gray);
rie = randintexc(255,255);       % Use this for random colors
%rie = 1:64;                     % Use this for sequential colors
for loop = 1:255
    h(loop,:) = hh(rie(loop),:);
end
figure(1)
fh = gcf;
clf;
set(gcf,'Color','White')
axis off

thet = 2*pi*rand(1,N);
rho = L*sqrt(rand(1,N));
X0 = rho.*cos(thet);
Y0 = rho.*sin(thet);

Vx0 = 0*Y0/L;   %1.5 for 500   2.0 for 700
Vy0 = -0*X0/L;
% X0 = L*2*(rand(1,N)-0.5);
% Y0 = L*2*(rand(1,N)-0.5);
% Vx0 = 0.5*sign(Y0);
% Vy0 = -0.5*sign(X0);
% Vx0 = zeros(1,N);
% Vy0 = zeros(1,N);

for nloop = 1:N
    y0(nloop) = X0(nloop);
    y0(nloop+N) = Y0(nloop);
    y0(nloop+2*N) = Vx0(nloop);
    y0(nloop+3*N) = Vy0(nloop);
end

T = 300;  %500
xp = zeros(1,N); yp = zeros(1,N);

for tloop = 1:T
    tloop
    
    delt = 0.005;
    tspan = [0 loop*delt];
    opts = odeset('RelTol',1e-2,'AbsTol',1e-5);
    [t,y] = ode45(@f5,tspan,y0,opts);
    
    %%%%%%%%% Plot Final Positions
    
    [szt,szy] = size(y);
    
    % Set nodes
    ind = 0; xpold = xp; ypold = yp;
    for nloop = 1:N
        ind = ind+1;
        xp(ind) = y(szt,ind+N);
        yp(ind) = y(szt,ind);
    end
    delxp = xp - xpold;
    delyp = yp - ypold;
    maxdelx = max(abs(delxp));
    maxdely = max(abs(delyp));
    maxdel = max(maxdelx,maxdely);
    
    rngx = max(xp) - min(xp);
    rngy = max(yp) - min(yp);
    maxrng = max(abs(rngx),abs(rngy));
    
    difepmx = maxdel/maxrng;
    
    crad = 2.5;
    subplot(1,2,1)
    gca;
    cla;
    
    % Draw nodes
    for nloop = 1:N
        rn = rand*63+1;
        colorval = ceil(64*nloop/N);
        
        rectangle('Position',[xp(nloop)-crad,yp(nloop)-crad,2*crad,2*crad],...
            'Curvature',[1,1],...
            'LineWidth',0.1,'LineStyle','-','FaceColor',h(colorval,:))
        
    end
    
    [syy,sxy] = size(y);
    y0(:) = y(syy,:);
    
    rnv = (2.0 + 2*tloop/T)*L;    % 2.0   1.5
    
    axis equal
    axis([-rnv rnv -rnv rnv])
    box on
    drawnow
    pause(0.01)
    
    KE = sum(y0(2*N+1:4*N).^2);
    
    Upot = 0;
    for nloop = 1:N
        for mloop = nloop+1:N
            dx = y0(nloop)-y0(mloop);
            dy = y0(nloop+N) - y0(mloop+N);
            dist = sqrt(dx^2+dy^2+eps^2);
            Upot = Upot + A/dist;
        end
    end
    
    Upoten = Upot;
    
    TotE = Upoten + KE;
    
    if tloop == 1
        TotE0 = TotE;
    end

    Upotent(tloop) = Upoten;
    KEn(tloop) = KE;
    TotEn(tloop) = TotE;
    
    xx = 1:tloop;
    subplot(1,2,2)
    plot(xx,KEn,xx,Upotent,xx,TotEn,'LineWidth',3)
    legend('KE','Upoten','TotE')
    axis([0 T -26000 22000])     % 3000 -6000 for 500   6000 -8000 for 700
    
    
    fh = figure(1);
    
    if mov_flag == 1
        frame = getframe(fh);
        writeVideo(aviobj,frame);
    end
    
end

if mov_flag == 1
    close(aviobj);
end

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
    function yd = f5(t,y)
        
        for n1loop = 1:N
            
            posx = y(n1loop);
            posy = y(n1loop+N);
            momx = y(n1loop+2*N);
            momy = y(n1loop+3*N);
            
            tempcx = 0; tempcy = 0;
            
            for n2loop = 1:N
                if n2loop ~= n1loop
                    cposx = y(n2loop);
                    cposy = y(n2loop+N);
                    cmomx = y(n2loop+2*N);
                    cmomy = y(n2loop+3*N);
                    
                    dis = sqrt((cposy-posy)^2 + (cposx-posx)^2 + eps^2);
                    CFx = 0.5*A*(posx-cposx)/dis^3 - 5e-5*momx/dis^4;
                    CFy = 0.5*A*(posy-cposy)/dis^3 - 5e-5*momy/dis^4;
                    
                    tempcx = tempcx + CFx;
                    tempcy = tempcy + CFy;
                    
                end
            end
                        
            ypp(n1loop) = momx;
            ypp(n1loop+N) = momy;
            ypp(n1loop+2*N) = tempcx - K*posx;
            ypp(n1loop+3*N) = tempcy - K*posy;
        end
        
        yd=ypp'; 
     
    end     % end f5

end     % end Nbody

Read more in Books by David D. Nolte at Oxford University Press

June 26, 2024September 5, 2025 by David D. Nolte

100 Years of Quantum Physics: The Statistics of Satyendra Nath Bose (1924)

One hundred years ago, in July of 1924, a brilliant Indian physicist changed the way that scientists count. Satyendra Nath Bose (1894 – 1974) mailed a letter to Albert Einstein enclosed with a manuscript containing a new derivation of Planck’s law of blackbody radiation. Bose had used a radical approach that went beyond the classical statistics of Maxwell and Boltzmann by counting the different ways that photons can fill a volume of space. His key insight was the indistinguishability of photons as quantum particles.

Today, the indistinguishability of quantum particles is the foundational element of quantum statistics that governs how fundamental particles combine to make up all the matter of the universe. At the time, neither Bose nor Einstein realized just how radical his approach was, until Einstein, using Bose’s idea, derived the behavior of material particles under conditions similar black-body radiation, predicting a new state of condensed matter [1]. It would take scientists 70 years to finally demonstrate “Bose-Einstein” condensation in a laboratory in Boulder, Colorado in 1995.

Early Days of the Photon

As outlined in a previous blog (see Who Invented the Quantum? Einstein versus Planck), Max Planck was a reluctant revolutionary. He was led, almost against his will, in 1900 to postulate a quantized interaction between electromagnetic radiation and the atoms in the walls of a black-body enclosure. He could not break free from the hold of classical physics, assuming classical properties for the radiation and assigning the quantum only to the “interaction” with matter. It was Einstein, five years later in 1905, who took the bold step of assigning quantum properties to the radiation field itself, inventing the idea of the “photon” (named years later by the American chemist Gilbert Lewis) as the first quantum particle.

Despite the vast potential opened by Einstein’s theory of the photon, quantum physics languished for nearly 20 years from 1905 to 1924 as semiclassical approaches dominated the thinking of Niels Bohr in Copenhagen, and Max Born in Göttingen, and Arnold Sommerfeld in Munich, as they grappled with wave-particle duality.

The existence of the photon, first doubted by almost everyone, was confirmed in 1915 by Robert Millikan’s careful measurement of the photoelectric effect. But even then, skepticism remained until Arthur Compton demonstrated experimentally in 1923 that the scattering of photons by electrons could only be explained if photons carried discrete energy and momentum in precisely the way that Einstein’s theory required.

Despite the success of Einstein’s photon by 1923, derivations of the Planck law still used a purely wave-based approach to count the number of electromagnetic standing waves that a cavity could support. Bose would change that by deriving the Planck law using purely quantum methods.

The Quantum Derivation by Bose

Satyendra Nath Bose was born in 1894 in Calcutta, the old British capital city of India, now Kolkata. He excelled at his studies, especially in mathematics, and received a lecturer post at the University of Calcutta from 1916 to 1921, when he moved into a professorship position at the new University of Dhaka.

One day, as he was preparing a class lecture on the derivation of Planck’s law,

he became dissatisfied with the usual way it was presented in textbooks, based on standing waves in the cavity, and he flipped the problem.

Rather than deriving the number of standing wave modes in real space, he considered counting the number of ways a photon would fill up phase space.

Phase space is the natural dynamical space of Hamiltonian systems [2], such as collections of quantum particles like photons, in which the axes of the space are defined by the positions and momenta of the particles. The differential volume of phase space dV_PS occupied by a single photon is given by

Using Einstein’s formula for the relationship between momentum and frequency

where h is Planck’s constant, yields

No quantum particle can have its position and momentum defined arbitrarily precisely because of Heisenberg’s uncertainty principle, requiring phase space volumes to be resolvable only to within a minimum reducible volume element given by h³.

Therefore, the number of states in phase space occupied by the single photon are obtained by dividing dV_PS by h³ to yield

which is half of the prefactor in the Planck law. Several comments are now necessary.

First, when Bose did this derivation, there was no Heisenberg Uncertainty relationship—that would come years later in 1927. Bose was guided, instead, by the work of Bohr and Sommerfeld and Ehrenfest who emphasized the role played by the action principle in quantum systems. Phase space dimensions are counted in units of action, and the quantized unit of action is given by Planck’s constant h, hence quantized volumes of action in phase space are given by h³. By taking this step, Bose was anticipating Heisenberg by nearly three years.

Second, Bose knew that his phase space volume was half of the prefactor in Planck’s law. But since he was counting states, he reasoned that this meant that each photon had two internal degrees of freedom. A possibility he considered to account for this was that the photon might have a spin that could be aligned, or anti-aligned, with the momentum of the photon [3, 4]. How he thought of spin is hard to fathom, because the spin of the electron, proposed by Uhlenbeck and Goudsmit, was still two years away.

But Bose was not finished. The derivation, so far, is just how much phase space volume is accessible to a single photon. The next step is to count the different ways that many photons can fill up phase space. For this he used (bringing in the factor of 2 for spin)

where p_n is the probability that a volume of phase space contains n photons, plus he used the usual conditions on energy and number

The probability for all the different permutations for how photons can occupy phase space is then given by

A third comment is now necessary: By assuming this probability, Bose was discounting situations where the photons could be distinguished from one another. This indistinguishability of quantum particles is absolutely fundamental to our understanding today of quantum statistics, but Bose was using it implicitly for the first time here.

The final distribution of photons at a given temperature T is found by maximizing the entropy of the system

subject to the conditions of photon energy and number. Bose found the occupancy probabilities to be

with a coefficient B to be found next by using this in the expression for the geometric series

yielding

Also, from the total number of photons

And, from the total energy

Bose obtained, finally

which is Planck’s law.

This derivation uses nothing by the counting of quanta in phase space. There are no standing waves. It is a purely quantum calculation—the first of its kind.

Enter Einstein

As usual with revolutionary approaches, Bose’s initial manuscript submitted to the British Philosophical Magazine was rejected. But he was convinced that he had attained something significant, so he wrote his letter to Einstein containing his manuscript, asking that if Einstein found merit in the derivation, then perhaps he could have it translated into German and submitted to the Zeitschrift für Physik. (That Bose would approach Einstein with this request seems bold, but they had communicated some years before when Bose had translated Einstein’s theory of General Relativity into English.)

Indeed, Einstein recognized immediately what Bose had accomplished, and he translated the manuscript himself into German and submitted it to the Zeitschrift on July 2, 1924 [5].

During his translation, Einstein did not feel that Bose’s conjecture about photon spin was defensible, so he changed the wording to attribute the factor of 2 in the derivation to the two polarizations of light (a semiclassical concept), so Einstein actually backtracked a little from what Bose originally intended as a fully quantum derivation. The existence of photon spin was confirmed by C. V. Raman in 1931 [6].

In late 1924, Einstein applied Bose’s concepts to an ideal gas of material atoms and predicted that at low temperatures the gas would condense into a new state of matter known today as a Bose-Einstein condensate [1]. Matter differs from photons because the conservation of atom number introduces a finite chemical potential to the problem of matter condensation that is not present in the Planck law.

Fig. 1 Experimental evidence for the Bose-Einstein condensate in an atomic vapor [7].

Paul Dirac, in 1945, enshrined the name of Bose by coining the phrase “Boson” to refer to a particle of integer spin, just as he coined “Fermion” after Enrico Fermi to refer to a particle of half-integer spin. All quantum statistics were encased by these two types of quantum particle until 1982, when Frank Wilczek coined the term “Anyon” to describe the quantum statistics of particles confined to two dimensions whose behaviors vary between those of a boson and of a fermion.

By David D. Nolte, June 26, 2024

References

[1] A. Einstein. “Quantentheorie des einatomigen idealen Gases”. Sitzungsberichte der Preussischen Akademie der Wissenschaften. 1: 3. (1925)

[2] D. D. Nolte, “The tangled tale of phase space,” Physics Today 63, 33-38 (2010).

[3] Partha Ghose, “The Story of Bose, Photon Spin and Indistinguishability” arXiv:2308.01909 [physics.hist-ph]

[4] Barry R. Masters, “Satyendra Nath Bose and Bose-Einstein Statistics“, Optics and Photonics News, April, pp. 41-47 (2013)

[5] S. N. Bose, “Plancks Gesetz und Lichtquantenhypothese”, Zeitschrift für Physik , 26 (1): 178–181 (1924)

[6] C. V. Raman and S. Bhagavantam, Ind. J. Phys. vol. 6, p. 353, (1931).

[7] Anderson, M. H.; Ensher, J. R.; Matthews, M. R.; Wieman, C. E.; Cornell, E. A. (14 July 1995). “Observation of Bose-Einstein Condensation in a Dilute Atomic Vapor”. Science. 269 (5221): 198–201.

February 14, 2024September 5, 2025 by David D. Nolte

100 Years of Quantum Physics: de Broglie’s Wave (1924)

One hundred years ago this month, in Feb. 1924, a hereditary member of the French nobility, Louis Victor Pierre Raymond, the 7th Duc de Broglie, published a landmark paper in the Philosophical Magazine of London [1] that revolutionized the nascent quantum theory of the day.

Prior to de Broglie’s theory of quantum matter waves, quantum physics had been mired in ad hoc phenomenological prescriptions like Bohr’s theory of the hydrogen atom and Sommerfeld’s theory of adiabatic invariants. After de Broglie, Erwin Schrödinger would turn the concept of matter waves into the theory of wave mechanics that we still practice today.

*Fig. 1 The 1924 paper by de Broglie in the Philosophical Magazine.*

The story of how de Broglie came to his seminal idea had an odd twist, based on an initial misconception that helped him get the right answer ahead of everyone else, for which he was rewarded with the Nobel Prize in Physics.

de Broglie’s Early Days

When Louis de Broglie was a student, his older brother Maurice (the 6^th Duc de Broglie) was already a practicing physicist making important discoveries in x-ray physics. Although Louis initially studied history in preparation for a career in law, and he graduated from the Sorbonne with a degree in history, his brother’s profession drew him like a magnet. He also read Poincaré at this critical juncture in his career, and he was hooked. He enrolled in the Faculty of Sciences for his advanced degree, but World War I side-tracked him into the signal corps, where he was assigned to the wireless station on top of the Eiffel Tower. He may have participated in the famous interception of a coded German transmission in 1918 that helped turn the tide of the war.

Beginning in 1919, Louis began assisting his brother in the well-equiped private laboratory that Maurice had outfitted in the de Broglie ancestral home. At that time Maurice was performing x-ray spectroscopy of the inner quantum states of atoms, and he was struck by the duality of x-ray properties that made them behave like particles under some conditions and like waves in others.

*Fig. 2 Maurice de Broglie in his private laboratory (Figure credit).*

*Fig. 3 Louis de Broglie (Figure credit)*

Through his close work with his brother, Louis also came to subscribe to the wave-particle duality of x-rays and chose the topic for his PhD thesis—and hence the twist that launched de Broglie backwards towards his epic theory.

de Broglie’s Massive Photons

Today, we say that photons have energy and momentum although they are massless. The momentum is a simple consequence of Einstein’s special relativity

And if m = 0, then

and momentum requires energy but not necessarily mass.

But de Broglie started out backwards. He was so convinced of the particle-like nature of the x-ray photons, that he first considered what would happen if the photons actually did have mass. He constructed a massive photon and compared its proper frequency with a Lorentz-boosted frequency observed in a laboratory. The frequency he set for the photon was like an internal clock, set by its rest-mass energy and by Bohr’s quantization condition

He then boosted it into the lab frame by time dilation

But the energy would be transformed according to

with a corresponding frequency

which is in direct contradiction with Bohr’s quantization condition. What is the resolution of this seeming paradox?

de Broglie’s Matter Wave

de Broglie realized that his “massive photon” must satisfy a condition relating the observed lab frequency to the transformed frequency, such that

This only made sense if his “massive photon” could be represented as a wave with a frequency

that propagated with a phase velocity given by c/β. (Note that β < 1 so that the phase velocity is greater than the speed of light, which is allowed as long as it does not transmit any energy.)

To a modern reader, this all sounds alien, but only because this work in early 1924 represented his first pass at his theory. As he worked on this thesis through 1924, finally defending it in November of that year, he refined his arguments, recognizing that when he combined his frequency with his phase velocity,

it yielded the wavelength for a matter wave to be

where p was the relativistic mechanical momentum of a massive particle.

Using this wavelength, he explained Bohr’s quantization condition as a simple standing wave of the matter wave. In the light of this derivation, de Broglie wrote

We are then inclined to admit that any moving body may be accompanied by a wave and that it is impossible to disjoin motion of body and propagation of wave.
pg. 450, Philosophical Magazine of London (1924)

Here was the strongest statement yet of the wave-particle duality of quantum particles. de Broglie went even further and connected the ideas of waves and rays through the Hamilton-Jacobi formalism, an approach that Dirac would extend several years later, establishing the formal connection between Hamiltonian physics and wave mechanics. Furthermore, de Broglie conceived of a “pilot wave” interpretation that removed some of Einstein’s discomfort with the random character of quantum measurement that ultimately led Einstein to battle Bohr in their famous debates, culminating in the iconic EPR paper that has become a cornerstone for modern quantum information science. After the wave-like nature of particles was confirmed in the Davisson-Germer experiments, de Broglie received the Nobel Prize in Physics in 1929.

*Fig. 4 A standing matter wave is a stationary state of constructive interference. This wavefunction is in the L = 5 quantum manifold of the hydrogen atom.*

Louis de Broglie was clearly ahead of his times. His success was partly due to his isolation from the dogma of the day. He was able to think without the constraints of preconceived ideas. But as soon as he became a regular participant in the theoretical discussions of his day, and bowed under the pressure from Copenhagen, his creativity essentially ceased. The subsequent development of quantum mechanics would be dominated by Heisenberg, Born, Pauli, Bohr and Schrödinger, beginning at the 1927 Solvay Congress held in Brussels.

By David D. Nolte, Feb. 14, 2024

[1] L. de Broglie, “A tentative theory of light quanta,” Philosophical Magazine 47, 446-458 (1924).

Einsteinian Gas Theory

The Zurich Seminar

The Christmas Breakthrough

The Schrödinger Wave Equation

Bibliography

Notes

Heisenberg’s Trajectory

Trajectory’s End

The Matrix

The Drei-Männer Quantum Mechanics Paper: Born, Heisenberg, and Jordan

Open Issues

Further Reading

References

Encyclopedia Article on Relativity

Anomalous Zeeman Effect

The Difference of Squares

The Bohr Model for Many Electrons

Pauli’s Breakthrough

Timeline:

References:

Early Days

Purdue University and Prof. Lark-Horowitz

Radiation Laboratory, MIT

Nuclear Magnetic Resonance

References and Notes

The Virial Theorem

Rudolph Clausius and his Virial Theorem

The Virial in Astrophysics

The Virial in Quantum Physics

References

Matlab Code

Early Days of the Photon

The Quantum Derivation by Bose

Enter Einstein

References

de Broglie’s Early Days

de Broglie’s Massive Photons

de Broglie’s Matter Wave