July 29, 2025August 5, 2025 by David D. Nolte

Anant K. Ramdas in the Golden Age of Physics

History of Dynamics, ScienceScape
Anant Ramdas, Deep-level Defects, Diamond, Eugene Haller, Faraday Rotation, History of Optics, History of Physics, Leo Falicov, Milly Dresselhaus, Quantum Synchronization, Raman Effect, Shallow Defects

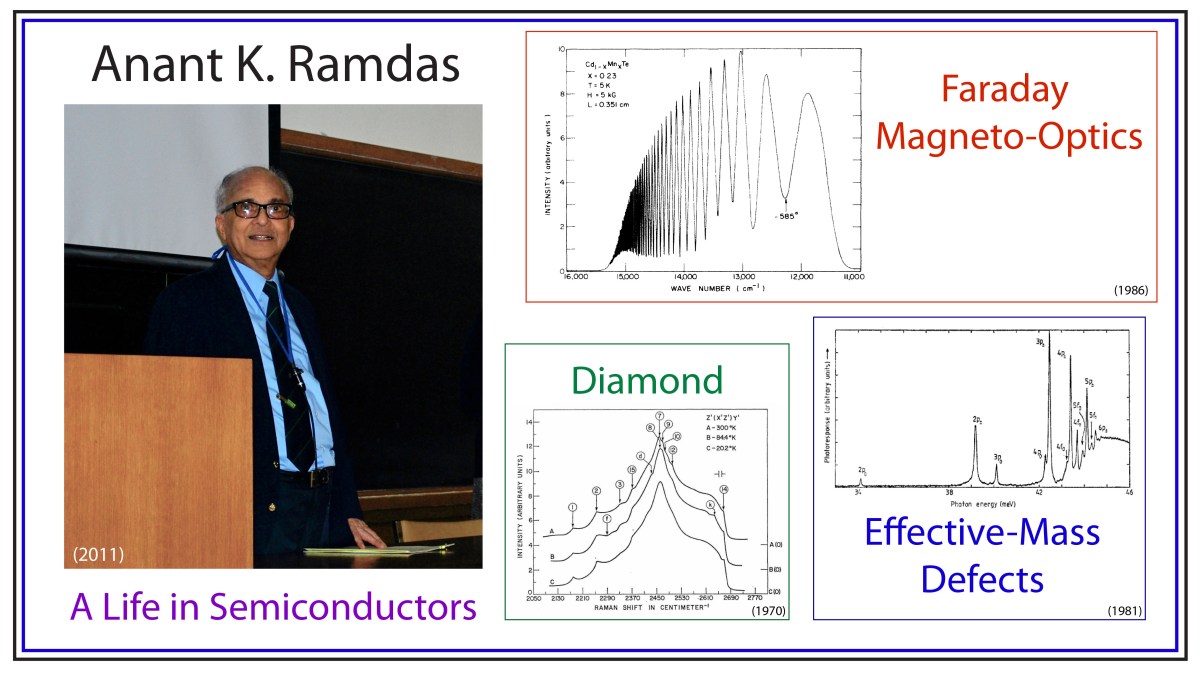
The physicist, as a gentleman and a scholar, who, in his leisure, pursues physics as both vocation and hobby, is an endangered species, though they once were endemic. Classic examples come from the turn of the last century, as Rayleigh and de Broglie and Raman built their own laboratories to follow their own ideas. These were giants in their fields. But there are also many quiet geniuses, enthralled with the life of ideas and the society of scientists, working into the late hours, following the paths that lead them forward through complex concepts and abstract mathematics as a labor of love.

One of these quiet geniuses, of late, was a colleague of mine and a friend, Anant K. Ramdas. He was the last PhD student of the Nobel Prize Laureate, C. V. Raman, and he may have been the last of his kind as a gentleman and a scholar physicist.

Anant K. Ramdas

Anant Ramdas was born in May, 1930, in Pune, India, not far from the megalopolis of Mumbai when it had just over a million inhabitants (the number is over 22 million today, nearly a hundred years later). His father, Lakshminarayanapuram A. Ramdas, was a scientist, a meteorologist who had studied under C. V. Raman at the University of Calcutta. Raman won the Nobel Prize in Physics the same year that Anant Ramdas was born.

Ramdas received his BS in Physics from the University of Pune in 1950, then followed in his father’s footsteps by studying for his MS (1953) and PhD (1956) degrees in Physics under Raman, who had established the Raman Institute in Bangalore, India.

While facing the decision, after his graduation, on what to do and where to go, Ramdas read a review article published by Prof. H. Y. Fan of Purdue University on infrared spectroscopy of semiconductors. After corresponding with Fan, and with the Purdue Physics department head, Prof. Karl Lark-Horowitz, Ramdas decided to accept the offer of a research associate (a post-doc position), and he prepared to leave India.

Within only a few months, he met and married his wife, Vasanti, and they hopped on a propeller plane to London that stopped along the way in Cairo, Beirut, Lebanon, and Paris before arriving in London. From there, they caught a cargo ship making a two-week passage across the Atlantic, after stopping at ports in France and Portugal. In New York City, they took a train to Chicago, getting off during a brief stop in the little corn-town of Lafayette, Indiana, home of Purdue University. It was 1956, and Anant and Vasanti were, ironically, the first Indians that some people in the Indiana town had ever seen.

Semiconductor Physics at Purdue

Semiconductors became the ascendent electronic material during the Second World War when it was discovered that their electrical properties were ideal for military radar applications. Many of the top physicists of the time worked at the “Rad Lab”, the Radiation Laboratory of MIT, and collaborations spread out across the US, including to the Physics Department at Purdue University. Researchers at Purdue were especially good at growing the semiconductor Germanium, which was used in radar rectifiers. The research was overseen by Lark-Horowitz.

After the war, semiconductor research continued to be a top priority in the Purdue Physics department as groups around the world competed to find ways to use semiconductors instead of vacuum tubes for information and control. Friendly competition often meant the exchange of materials and samples, and sometime in early 1947, several Germanium samples were shipped to the group of Bardeen and Brattain at Bell Labs, where, several months later, they succeeded in making the first point contact transistor using Germanium (with some speculation today that it may have been with the samples sent from Purdue). It was a close thing. Ralph Bray, a professor at Purdue, had seen nonlinear current dependences in the Purdue-grown Germanium samples that were precursers of transistor action, but Bell made the announcement before Bray had a chance to take the next step. Lark-Horowitz (and Bray) never forgot how close Purdue had come to making the invention themselves [1].

Bray_1997_Electrochem._Soc._Interface_6_24 Download

In 1948, Lark-Horowitz hired H. Y. Fan, who had received his PhD at MIT in 1937 and had been teaching at Tsinghua University in China. Fan was an experimental physicist specializing in the infrared properties of semiconductors, and when Ramdas arrived at Purdue in 1956, he worked directly under Fan. They published their definitive work on the infrared absorption of irradiated silicon in 1959 [2].

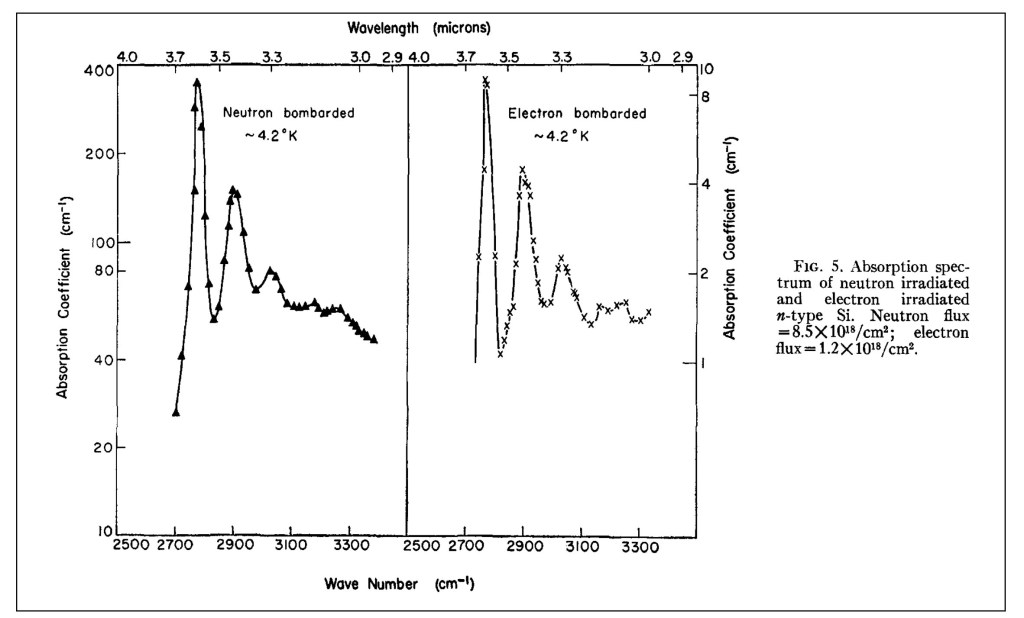
Absorption spectrum of “effective-mass” shallow defect levels in irradiated silicon.

FanRamdas Download

One day, while Ramdas was working in Fan’s lab, Lark-Horowitz stopped by, as he was accustomed to do, and he casually asked if Ramdas would be interested in becoming a professor at Purdue. Ramdas of course said “Yes”, and Lark-Horowitz gave him the job on the spot. Ramdas was appointed as an assistant professor in 1960. These things were less formal in those days, and it was only later that Ramdas learned that Fan had already made a strong case for him.

The Golden Age of Physics

The period from 1960 to 2015, which spanned Ramdas’ career, start to finish, might be called “The Golden Age of Physics”.

This time span saw the completion of the Standard Model of particle physics with the theory of quarks (1964), the muon neutrino (1962), electro-weak unification (1968), quantum chromodynamics (1970s), the tau lepton (1975), the bottom quark (1977), the top quark (1995), the W and Z bosons (1983), the tau neutrino (2000), neutrino mass oscillations (2004), and of course capping it off with the detection of the Higgs boson (2012).

This was the period in solid state physics that saw the invention of the laser (1960), the quantum Hall effect (1980), the fractional quantum Hall effect (1982), scanning tunneling microscopy (1981), quasi-crystals (1982), high-temperature superconductors (1986), and graphene (2005).

This was also the period when astrophysics witnessed the discovery of the Cosmic Background Radiation (1964), the first black hole (1964), pulsars (1967), confirmation of dark matter (1970s), inflationary cosmology (1980s), Baryon Acoustic Oscillations (2005), and capping the era off with the detection of gravitational waves (2015).

The period from 1960 – 2015 stands out relative to the “first” Golden Age of Physics from 1900 – 1930 because this later phase is when the grand programs from early in the century were brought largely to completion.

But these are the macro-events of physics from 1960-2015. This era was also a Golden Age in the micro-events of the everyday lives of the physicists. It is this personal aspect where this later era surpassed the earlier era (when only a handful of physicists were making progress). In the later part of the century, small armies of physicists were advancing rapidly along all the frontiers at the same time, and doing it with the greatest focus.

This was when a single NSF grant could support a single physicist with several grad students and an undergraduate or two. The grants could be renewed with near certainty, as long as progress was made and papers were published. Renewal applications, in those days, were three pages. Contrast that to today when 25 pages need to be honed to perfection—and then the renewal rate is only about 10% (soon to be even lower with the recent budget cuts to science in the USA). In those earlier days, the certainty of success, and the absence of the burden of writing multiple long grant proposals, bred confidence to dispose of the conventional, to try anything new. In other words, the vast amount of time spent by physicists during this Golden Age was in the pursuit of physics, in the classroom and in the laboratory.

And this was the time when Anant Ramdas and his cohort—Sergio Rodriguez, Peter Fisher, Jacek Furdyna, Eugene Haller, the Chandrasekhar’s, Manuel Cardona, and the Dresselhaus’s—rode the wave of semiconductor physics when money was easy, good students were plentiful, and a vibrant intellectual community rallied around important problems.

Selected Topics of Research from Anant Ramdas

It is impossible to give justice to the breadth and depth of research performed by Anant over his career. So here is my selection of some of my favorite examples of his work:

Diamond

Anant had a life-long fascination for diamonds. As a rock and gem collector, he was fond of telling stories about the famous Cullinan diamond (weighed 1.3 pounds as a raw diamond at 3000 carats) and the blue Hope diamond (discovered in India). One of his earliest and most cited papers was on the Raman spectrum of Diamond [3], and he published several papers on his favorite color for diamonds—Blue [4]!

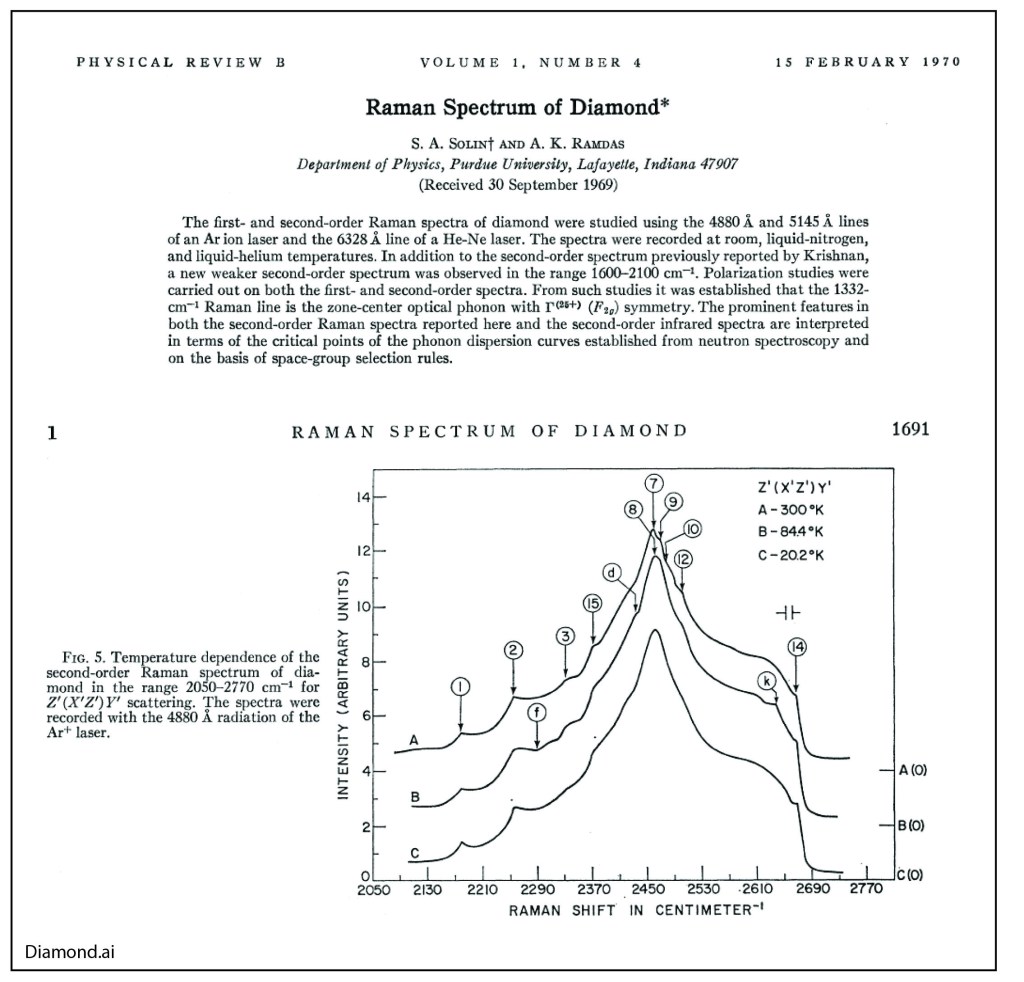
Raman Spectrum of Diamond.

DiamondPhysRevB.1.1687 Download

His work on diamond helped endear Anant with the husband-wife team of Milly Dresselhaus and Gene Dresselhaus at MIT. Milly was the “Queen” of carbon, known for her work on graphite, carbon nanotubes and Fullerenes. Purdue had made an offer of an assistant professorship to Gene Dresselhaus when the two were looking for faculty positions after their post-docs at the University of Chicago, but Purdue would not give Milly a position (she was viewed as a “trailing” spouse). Anant was already at Purdue at that time and got to know both of them, maintaining a life-long friendship. Milly went on to become the president of the APS and was elected a member of the National Academy of Sciences, the National Academy of Engineering and the American Academy of Arts and Sciences.

Magneto-Optics

Purdue was a hot-bed of II-VI semiconductor research in the 1980’s, spearheaded by Jacek Furdyna. The substitution of the magnetic ion Mn for Zn, Cd or Hg created a unique class of highly magnetic semiconductors. Anant was the resident expert on the optical properties of the materials and collected one of the best examples of Giant Faraday Rotation [5].

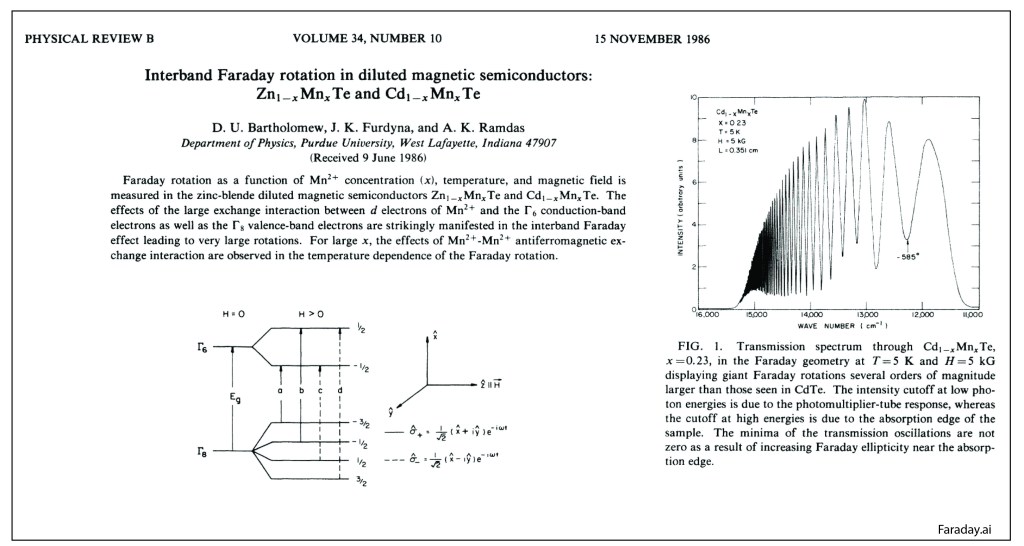
Giant Faraday Effect in CdMnTe

FaradayPhysRevB Download

Anant and the Purdue team were the world leaders in the physics and materials science of diluted magnetic semiconductors.

Shallow Defects in Semiconductors

My own introduction to Anant was through his work on shallow effective-mass defect states in semiconductors. I was working towards my PhD with Eugene ‘Gene” Haller at Lawrence Berkeley Lab (LBL) in the early 1980’s, and Gene was an expert on the spectroscopy of the shallow levels in Germanium. My co-physics graduate student colleague was Joe Kahn, and the two of us were tasked with studying the review article that Anant had written with his long-time theoretical collaborator Sergio Rodriguez on the physics of effective-mass shallow defects in semiconductors [6]. We called it “The Bible”, and spent months studying it. Gene Haller’s principal technique was photothermal ionization spectroscopy (PTIS), and Joe was building the world’s finest PTIS instrument. Joe met Anant for dinner one night at the March meeting of the APS in 1986, and when he got back to the room, he waxed poetic about Anant for an hour. It was like he had met his hero. I don’t remember how I missed that dinner, so my personal introduction to Anant Ramdas would have to wait.

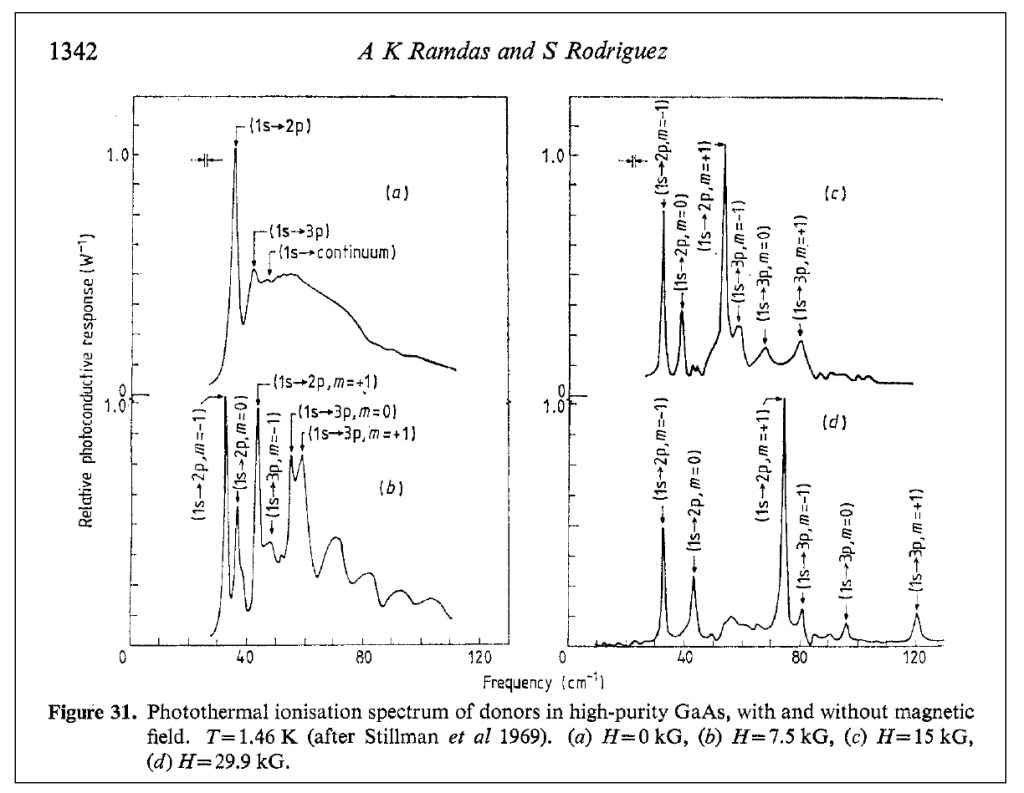
PTIS spectra of donors in GaAs

Ramdas_1981_Rep._Prog._Phys Download

My own research went into deep-level transient spectroscopy (DLTS) working with Gene and his group theorist, Wladek Walukiewicz, where we discovered a universal pressure derivative in III-V semiconductors. This research led me to a post-doc position at Bell Labs under Alastair Glass and later to a faculty position at Purdue, where I did finally meet Anant, who became my long-time champion and mentor. But Joe had stayed with the shallow defects, and in particular defects that showed interesting dynamical properties, known as tunneling defects.

Dynamic Defects in Semiconductors

Dynamic defects in semiconductors are multicomponent defects (often involving vacancies or interstitial defects) in which one of the components tunnels quantum mechanically, or hops, rapidly on a time scale short compared to the measurement interaction time (electric dipole transition), so that the measurement sees increased symmetry compared to the instantaneous low-symmetry configuration of the defect.

Eugene Haller and his physics theory collaborator, Leo Falicov, were pioneers in tunneling defects related to hydrogen, building on earlier work by George Watkins who studied dynamical defects using EPR measurements. In my early days doing research under Eugene, we thought we had discovered a dynamical effect in FeB defects in silicon, and I spent two very interesting weeks at Lehigh University, visiting Watkins, to test out our idea, but it turned out to be a static effect. Later, Joe Kahn found that some of the early hydrogen defects in Germanium that Gene and Leo had proposed as dynamical defects were also, in fact, static. So the class of dynamical defects in semiconductors was actually shrinking over time rather than expanding. Joe did go on to find clear proof of a hydrogen-related dynamical defect in Germanium, saving the Haller-Falicov theory from the dust bin of Physics History.

In 2006 and in 2008, Ramdas was working on Oxygen-related defect complexes in CdSe when his student, G. Chen [7-8], discovered a temperature-induced symmetry raising. It showed clear evidence for a lower symmetry defect that converged into a higher symmetry mode at high temperatures, very much in agreement with the Haller-Falicov theory of dynamical symmetry raising.

At that time, I was developing my course notes for my textbook Introduction to Modern Dynamics, where some of the textbook problems in synchronization looked just like Anant’s data. Using a temperature-dependent coupling in a model of nonlinear (anharmonic) oscillators, I obtained the following fits (solid curves) to the Ramdas data (data points):

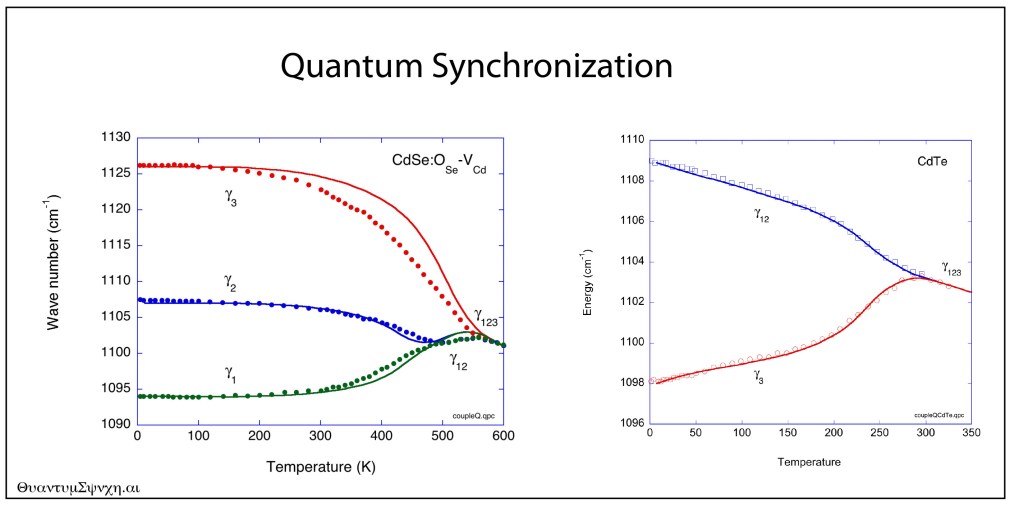
Quantum synchronization in CdSe and CdTe.

DoubletPhysRevLett Download

TripletPhysRevLett Download

The fit looks too good to be a coincidence, and Anant and I debated on whether the Haller-Falicov theory, or a theory based on nonlinear synchronization, would be better descriptions of the obviously dynamical properties of these defects. Alas, Anant is now gone, and so are Gene and Leo, so I am the last one left thinking about these things.

Beyond the Golden Age?

Anant Ramdas was fortunate to have spent his career during the Golden Age of Physics, when the focus was on the science and on the physics, as healthy communities helped support one another in friendly competition. He was a gentleman scholar, an avid reader of books on history and philosophy, much of it (but not all) on the history and philosophy of physics. His “Coffee Club” at 9:30 AM every day in the Physics Department at Purdue was a must-not-miss event that was attended by all of the Old Guard as well as by myself, where the topics of conversation ran the gamut, presided over by Anant. He had his NSF grant, year after year (and a few others), and that was all he needed to delve into the mysteries of the physics of semiconductors.

Is that age over? Was Anant one of the last of that era? I can only imagine what he would say about the current war against science and against rationality raging across the USA right now, and the impending budget cuts to all the science institutes. He spent his career and life upholding the torch of enlightenment. Today, I fear he would be holding it in the dark. He passed away Thanksgiving, 2024.

Vasanti and Anant, 2022.

References

[1] Ralph Bray, “A Case Study in Serendipity”, The Electrochemical Society, Interface, Spring 1997.

[2] H. Y. Fan and A. K. Ramdas, “INFRARED ABSORPTION AND PHOTOCONDUCTIVITY IN IRRADIATED SILICON,” Journal of Applied Physics, Article vol. 30, no. 8, pp. 1127-1134, 1959, doi: 10.1063/1.1735282.

[3] S. A. Solin and A. K. Ramdas, “RAMAN SPECTRUM OF DIAMOND,” Physical Review B, Article vol. 1, no. 4, pp. 1687-&, 1970, doi: 10.1103/PhysRevB.1.1687

[4] H. J. Kim, Z. Barticevic, A. K. Ramdas, S. Rodriguez, M. Grimsditch, and T. R. Anthony, “Zeeman effect of electronic Raman lines of accepters in elemental semiconductors: Boron in blue diamond,” Physical Review B, Article vol. 62, no. 12, pp. 8038-8052, Sep 2000, doi: 10.1103/PhysRevB.62.8038.

[5] D. U. Bartholomew, J. K. Furdyna, and A. K. Ramdas, “INTERBAND FARADAY-ROTATION IN DILUTED MAGNETIC SEMICONDUCTORS – ZN1-XMNXTE AND CD1-XMNXTE,” Physical Review B, Article vol. 34, no. 10, pp. 6943-6950, Nov 1986, doi: 10.1103/PhysRevB.34.6943.

[6] A. K. Ramdas and S. Rodriguez, “SPECTROSCOPY OF THE SOLID-STATE ANALOGS OF THE HYDROGEN-ATOM – DONORS AND ACCEPTORS IN SEMICONDUCTORS,” Reports on Progress in Physics, Review vol. 44, no. 12, pp. 1297-1387, 1981, doi: 10.1088/0034-4885/44/12/002

[7] G. Chen, I. Miotkowski, S. Rodriguez, and A. K. Ramdas, “Stoichiometry driven impurity configurations in compound semiconductors,” Physical Review Letters, Article vol. 96, no. 3, Jan 2006, Art no. 035508, doi: 10.1103/PhysRevLett.96.035508.

[8] G. Chen, J. S. Bhosale, I. Miotkowski, and A. K. Ramdas, “Spectroscopic Signatures of Novel Oxygen-Defect Complexes in Stoichiometrically Controlled CdSe,” Physical Review Letters, Article vol. 101, no. 19, Nov 2008, Art no. 195502, doi: 10.1103/PhysRevLett.101.195502.

Other Notable Papers:

[9] E. S. Oh, R. G. Alonso, I. Miotkowski, and A. K. Ramdas, “RAMAN-SCATTERING FROM VIBRATIONAL AND ELECTRONIC EXCITATIONS IN A II-VI QUATERNARY COMPOUND – CD1-X-YZNXMNYTE,” Physical Review B, Article vol. 45, no. 19, pp. 10934-10941, May 1992, doi: 10.1103/PhysRevB.45.10934.

[10] R. Vogelgesang, A. K. Ramdas, S. Rodriguez, M. Grimsditch, and T. R. Anthony, “Brillouin and Raman scattering in natural and isotopically controlled diamond,” Physical Review B, Article vol. 54, no. 6, pp. 3989-3999, Aug 1996, doi: 10.1103/PhysRevB.54.3989.

[11] M. H. Grimsditch and A. K. Ramdas, “BRILLOUIN-SCATTERING IN DIAMOND,” Physical Review B, Article vol. 11, no. 8, pp. 3139-3148, 1975, doi: 10.1103/PhysRevB.11.3139.

[12] E. S. Zouboulis, M. Grimsditch, A. K. Ramdas, and S. Rodriguez, “Temperature dependence of the elastic moduli of diamond: A Brillouin-scattering study,” Physical Review B, Article vol. 57, no. 5, pp. 2889-2896, Feb 1998, doi: 10.1103/PhysRevB.57.2889.

[13] A. K. Ramdas, S. Rodriguez, M. Grimsditch, T. R. Anthony, and W. F. Banholzer, “EFFECT OF ISOTOPIC CONSTITUTION OF DIAMOND ON ITS ELASTIC-CONSTANTS – C-13 DIAMOND, THE HARDEST KNOWN MATERIAL,” Physical Review Letters, Article vol. 71, no. 1, pp. 189-192, Jul 1993, doi: 10.1103/PhysRevLett.71.189.

September 25, 2024September 5, 2025 by David D. Nolte

Edward Purcell: From Radiation to Resonance

As the days of winter darkened in 1945, several young physicists huddled in the basement of Harvard’s Research Laboratory of Physics, nursing a high field magnet to keep it from overheating and dumping its field. They were working with bootstrapped equipment—begged, borrowed or “stolen” from various labs across the Harvard campus. The physicist leading the experiment, Edward Mills Purcell, didn’t even work at Harvard—he was still on the payroll of the Radiation Laboratory at MIT, winding down from its war effort on radar research for the military in WWII, so the Harvard experiment was being done on nights and weekends.

Just before Christmas, 1945, as college students were fleeing campus for the first holiday in years without war, the signal generator, borrowed from a psychology lab, launched an electromagnetic pulse into simple paraffin—and disappeared! It had been absorbed by the nuclear spins of the copious number of hydrogen nuclei (protons) in the wax.

The experiment was simple, unfunded, bootstrapped—and it launched a new field of physics that ultimately led to magnetic resonance imaging (MRI) that is now the workhorse of 3D medical imaging.

This is the story, in Purcell’s own words, of how he came to the discovery of nuclear magnetic resonance in solids, for which he was awarded the Nobel Prize in Physics in 1952.

Early Days

Edward Mills Purcell (1912 – 1997) was born in a small town in Illinois, the son of a telephone businessman, and some of his earliest memories were of rummaging around in piles of telephone equipment—wires and transformers and capacitors. He especially like the generators:

“You could always get plenty of the bell-ringing generators that were in the old telephones, which consisted of a series of horseshoe magnets making the stator field and an armature that was wound with what must have been a mile of number 39 wire or something like that… These made good shocking machines if nothing else.”

His science education in the small town was modest, mostly chemistry, but he had a physics teacher, a rare woman at that time, who was open to searching minds. When she told the students that you couldn’t pull yourself up using a single pulley, Purcell disagreed and got together with a friend:

“So we went into the barn after school and rigged this thing up with a seat and hooked the spring scales to the upgoing rope and then pulled on the downcoming rope.”

The experiment worked, of course, with the scale reading half the weight of the boy. When they rushed back to tell the physics teacher, she accepted their results immediately—demonstration trumped mere thought, and Purcell had just done his first physics experiment.

However, physics was not a profession in the early 1920’s.

“In the ’20s the idea of chemistry as a science was extremely well publicized and popular, so the young scientist of shall we say 1928 — you’d think of him as a chemist holding up his test tube and sighting through it or something…there was no idea of what it would mean to be a physicist.

The name Steinmetz was more familiar and exciting than the name Einstein, because Steinmetz was the famous electrical engineer at General Electric and was this hunchback with a cigar who was said to know the four-place logarithm table by heart.”

Purdue University and Prof. Lark-Horowitz

Purcell entered Purdue University in the Fall of 1929. The University had only 4500 students who paid $50 a year to attend. He chose a major in electrical engineering, because

“Being a physicist…I don’t remember considering that at that time as something you could be…you couldn’t major in physics. You see, Purdue had electrical, civil, mechanical and chemical engineering. It had something called the School of Science, and you could graduate, having majored in science.”

But he was drawn to physics. The Physics Department at Purdue was going through a Renaissance under the leadership of its new department head Prof. Lark-Horovitz

“His [Lark-Horovitz] coming to Purdue was really quite important for American physics in many ways… It was he who subsequently over the years brought many important and productive European physicists to this country; they came to Purdue, passed through. And he began teaching; he began having graduate students and teaching really modern physics as of 1930, in his classes.”

Purcell attended Purdue during the early years of the depression when some students didn’t have enough money to find a home:

“People were also living down there in the cellar, sleeping on cots in the research rooms, because it was the Depression and some of the graduate students had nowhere else to live. I’d come in in the morning and find them shaving.”

Lark-Horovitz was a demanding department chair, but he was bringing the department out of the dark ages and into the modern research world.

“Lark-Horovitz ran the physics department on the European style: a pyramid with the professor at the top and everybody down below taking orders and doing what the professor thought ought to be done. This made working for him rather difficult. I was insulated by one layer from that because it was people like Yearian, for whom I was working, who had to deal with the Lark. “

Hubert Yearian had built a 20-kilovolt electron diffraction camera, a Debye-Scherrer transmission camera, just a few years after Davisson and Germer had performed the Nobel-prize winning experiment at Bell Labs that proved the wavelike nature of electrons. Purcell helped Yearian build his own diffraction system, and recalled:

“When I turned on the light in the dark room, I had Debye-Scherrer rings on it from electron diffraction — and that was only five years after electron diffraction had been discovered. So it really was right in the forefront. And as just an undergraduate, to be able to do that at that time was fantastic.”

Purcell graduated from Purdue in 1933 and from contacts through Lark-Horovitz he was able to spend a year in the physics department at Karlsruhe in Germany. He returned to the US in 1934 to enter graduate scool in physics at Harvard, working under Kenneth Bainbridge. His thesis topic was a bit of a bust, a dusty old problem in classical electrostatics that was a topic far older than the electron diffraction he worked on at Purdue. But it was enough to get him his degree in 1938, and he stayed on at Harvard as a faculty instructor until the war broke out.

Radiation Laboratory, MIT

In the Fall at the end of 1940 the Radiation Lab at MIT was launched and began vacuuming up all the unattached physicists in the United States, and Purcell was one of them. The radiation lab also vacuumed up some of the top physicists in the country, like Isidor Rabi from Columbia, to supervise the growing army of scientists that were committed to the war effort—even before the US was in the war.

“Our mission was to make a radar for a British night fighter using 10-centimeter magnetron that had been discovered at Birmingham.”

This research turned Purcell and his cohort into experts in radio-frequency electronics and measurement. He worked closely with Rabi (Nobel Prize 1944) and Norman Ramsey (Nobel Prize 1989) and Jerrold Zacharias, who were in the midst of measuring resonances in molecular beams. The names at the Rad Lab was like reading a Who’s Who of physics at that time:

“And then there was the theoretical group, which was also under Rabi. Most of their theory was concerned with electromagnetic fields and signal to noise, things of that sort. George Uhlenbeck was in charge of it for quite a long time, and Bethe was in it for a while; Schwinger was in it; Frank Carlson; David Saxon, now president of the University of California; Goudsmit also.”

Nuclear Magnetic Resonance

The research by Rabi had established the physics of resonances in molecular beams, but there were serious doubts that such phenomena could exist in solids. This became one of the Holy Grails of physics, with only a few physicists across the country with the skill and understanding to make a try to observe it in the solid state.

Many of the physicists at the Rad Lab were wondering what they should do next, after the war was over.

“Came the end of the war and we were all thinking about what shall we do when we go back and start doing physics. In the course of knocking around with these people, I had learned enough about what they had done in molecular beams to begin thinking about what can we do in the way of resonance with what we’ve learned. And it was out of that kind of talk that I was struck with the idea for what turned into nuclear magnetic resonance.”

“Well, that’s how NMR started, with that idea which, as I say, I can trace back to all those indirect influences of talking with Rabi, Ramsey and Zacharias, thinking about what we should do next.

“We actually did the first NMR experiment here [Harvard], not at MIT. But I wasn’t officially back. In fact, I went around MIT trying to borrow a magnet from somebody, a big magnet, get access to a big magnet so we could try it there and I didn’t have any luck. So I came back and talked to Curry Street, and he invited us to use his big old cosmic ray magnet which was out in the shed. So I didn’t ask anybody else’s permission. I came back and got the shop to make us some new pole pieces, and we borrowed some stuff here and there. We borrowed our signal generator from the Psycho Acoustic Lab that Smitty Stevens had. I don’t know that it ever got back to him. And some of the apparatus was made in the Radiation Lab shops. Bob Pound got the cavity made down there. They didn’t have much to do — things were kind of closing up — and so we bootlegged a cavity down there. And we did the experiment right here on nights and week-ends.

This was in December, 1945.

“Our first experiment was done on paraffin, which I bought up the street at the First National store between here and our house. For paraffin we thought we might have to deal with a relaxation time as long as several hours, and we were prepared to detect it with a signal which was sufficiently weak so that we would not upset the spin temperature while applying the r-f field. And, in fact, in the final time when the experiment was successful, I had been over here all night … nursing the magnet generator along so as to keep the field on for many hours, that being in our view a possible prerequisite for seeing the resonances. Now, it turned out later that in paraffin the relaxation time is actually 10^-4 seconds. So I had the magnet on exactly 10⁸ times longer than necessary!

The experiment was completed just before Christmas, 1945.

E. M. Purcell, H. C. Torrey, and R. V. Pound, “RESONANCE ABSORPTION BY NUCLEAR MAGNETIC MOMENTS IN A SOLID,” Physical Review 69, 37-38 (1946).

“But the thing that we did not understand, and it gradually dawned on us later, was really the basic message in the paper that was part of Bloembergen’s thesis … came to be known as BPP (Bloembergen, Purcell and Pound). [This] was the important, dominant role of molecular motion in nuclear spin relaxation, and also its role in line narrowing. So that after that was cleared up, then one understood the physics of spin relaxation and understood why we were getting lines that were really very narrow.”

Diagram of the microwave cavity filled with paraffin.

This was the discovery of nuclear magnetic resonance (NMR) for which Purcell shared the 1952 Nobel Prize in physics with Felix Bloch.

David D. Nolte is the Edward M. Purcell Distinguished Professor of Physics and Astronomy, Purdue University. Sept. 25, 2024

References and Notes

• The quotes from EM Purcell are from the “Living Histories” interview in 1977 by the AIP.

• K. Lark-Horovitz, J. D. Howe, and E. M. Purcell, “A new method of making extremely thin films,” Review of Scientific Instruments 6, 401-403 (1935).

• E. M. Purcell, H. C. Torrey, and R. V. Pound, “RESONANCE ABSORPTION BY NUCLEAR MAGNETIC MOMENTS IN A SOLID,” Physical Review 69, 37-38 (1946).

• National Academy of Sciences Biographies: Edward Mills Purcell

Read more in Books by David Nolte at Oxford University Press

November 9, 2023August 16, 2025 by David D. Nolte

Timelines in the History of Light and Interference

Light is one of the most powerful manifestations of the forces of physics because it tells us about our reality. The interference of light, in particular, has led to the detection of exoplanets orbiting distant stars, discovery of the first gravitational waves, capture of images of black holes and much more. The stories behind the history of light and interference go to the heart of how scientists do what they do and what they often have to overcome to do it. These time-lines are organized along the chapter titles of the book Interference. They follow the path of theories of light from the first wave-particle debate, through the personal firestorms of Albert Michelson, to the discoveries of the present day in quantum information sciences.

Thomas Young Polymath: The Law of Interference
The Fresnel Connection: Particles versus Waves
At Light Speed: The Birth of Interferometry
After the Gold Rush: The Trials of Albert Michelson
Stellar Interference: Measuring the Stars
Across the Universe: Exoplanets, Black Holes and Gravitational Waves
Two Faces of Microscopy: Diffraction and Interference
Holographic Dreams of Princess Leia: Crossing Beams
Photon Interference: The Foundations of Quantum Communication
The Quantum Advantage: Interferometric Computing

1. Thomas Young Polymath: The Law of Interference

Thomas Young was the ultimate dabbler, his interests and explorations ranged far and wide, from ancient egyptology to naval engineering, from physiology of perception to the physics of sound and light. Yet unlike most dabblers who accomplish little, he made original and seminal contributions to all these fields. Some have called him the “Last Man Who Knew Everything“.

Topics: The Law of Interference. The Rosetta Stone. Benjamin Thompson, Count Rumford. Royal Society. Christiaan Huygens. Pendulum Clocks. Icelandic Spar. Huygens’ Principle. Stellar Aberration. Speed of Light. Double-slit Experiment.

1629 – Huygens born (1629 – 1695)

1642 – Galileo dies, Newton born (1642 – 1727)

1655 – Huygens ring of Saturn

1657 – Huygens patents the pendulum clock

1666 – Newton prismatic colors

1666 – Huygens moves to Paris

1669 – Bartholin double refraction in Icelandic spar

1670 – Bartholinus polarization of light by crystals

1671 – Expedition to Hven by Picard and Rømer

1673 – James Gregory bird-feather diffraction grating

1673 – Huygens publishes Horologium Oscillatorium

1675 – Rømer finite speed of light

1678 – Huygens and two crystals of Icelandic spar

1681 – Huygens returns to the Hague

1689 – Huyens meets Newton

1690 – Huygens Traite de la Lumiere

1695 – Huygens dies

1704 – Newton’s Opticks

1727 – Bradley abberation of starlight

1746 – Euler Nova theoria lucis et colorum

1773 – Thomas Young born

1786 – François Arago born (1786 – 1853)

1787 – Joseph Fraunhofer born (1787 – 1826)

1788 – Fresnel born in Broglie, Normandy (1788 – 1827)

1794 – École Polytechnique founded in Paris by Lazar Carnot and Gaspard Monge, Malus enters the Ecole

1794 – Young elected member of the Royal Society

1794 – Young enters Edinburg (cannot attend British schools because he was Quaker)

1795 – Young enters Göttingen

1796 – Young receives doctor of medicine, grand tour of Germany

1797 – Young returns to England, enters Emmanual College (converted to Church of England)

1798 – The Directory approves Napoleon’s Egyptian campaign, Battle of the Pyramids, Battle of the Nile

1799 – Young graduates from Cambridge

1799 – Royal Institution founded

1799 – Young Outlines

1800 – Young Sound and Light read to Royal Society,

1800 – Young Mechanisms of the Eye (Bakerian Lecture of the Royal Society)

1801 – Young Theory of Light and Colours, three color mechanism (Bakerian Lecture), Young considers interference to cause the colored films, first estimates of the wavelengths of different colors

1802 – Young begins series of lecturs at the Royal Institution (Jan. 1802 – July 1803)

1802 – Young names the principle (Law) of interference

1803 – Young’s 3^rd Bakerian Lecture, November. Experiments and Calculations Relative Physical to Optics, The Law of Interference

1807 – Young publishes A course of lectures on Natural Philosophy and the Mechanical Arts, based on Royal Institution lectures, two-slit experiment described

1808 – Malus polarization

1811 – Young appointed to St. Georges hospital

1813 – Young begins work on Rosetta stone

1814 – Young translates the demotic script on the stone

1816 – Arago visits Young

1818 – Young’s Encyclopedia article on Egypt

1822 – Champollion publishes translation of hieroglyphics

1827 – Young elected foreign member of the Institute of Paris

1829 – Young dies

2. The Fresnel Connection: Particles versus Waves

Augustin Fresnel was an intuitive genius whose talents were almost squandered on his job building roads and bridges in the backwaters of France until he was discovered and rescued by Francois Arago.

Topics: Particles versus Waves. Malus and Polarization. Agustin Fresnel. Francois Arago. Diffraction. Daniel Bernoulli. The Principle of Superposition. Joseph Fourier. Transverse Light Waves.

1665 – Grimaldi diffraction bands outside shadow

1673 – James Gregory bird-feather diffraction grating

1675 – Römer finite speed of light

1704 – Newton’s Optics

1727 – Bradley abberation of starlight

1774 – Jean-Baptiste Biot born

1786 – David Rittenhouse hairs-on-screws diffraction grating

1786 – François Arago born (1786 – 1853)

1787 – Fraunhofer born (1787 – 1826)

1788 – Fresnel born in Broglie, Normandy (1788 – 1827)

1790 – Fresnel moved to Cherbourg

1794 – École Polytechnique founded in Paris by Lazar Carnot and Gaspard Monge

1804 – Fresnel attends Ecole polytechnique in Paris at age 16

1806 – Fresnel graduated and attended the national school of bridges and highways

1808 – Malus polarization

1809 – Fresnel graduated from Les Ponts

1809 – Arago returns from captivity in Algiers

1811 – Arago publishes paper on particle theory of light

1811 – Arago optical ratotory activity (rotation)

1814 – Fraunhofer spectroscope (solar absorption lines)

1815 – Fresnel meets Arago in Paris on way home to Mathieu (for house arrest)

1815 – Fresnel first paper on wave properties of diffraction

1816 – Fresnel returns to Paris to demonstrate his experiments

1816 – Arago visits Young

1816 – Fresnel paper on interference as origin of diffraction

1817 – French Academy announces its annual prize competition: topic of diffraction

1817 – Fresnel invents and uses his “Fresnel Integrals”

1819 – Fresnel awarded French Academy prize for wave theory of diffraction

1819 – Arago and Fresnel transverse and circular (?) polarization

1821 – Fraunhofer diffraction grating

1821 – Fresnel light is ONLY transverse

1821 – Fresnel double refraction explanation

1823 – Fraunhofer 3200 lines per Paris inch

1826 – Publication of Fresnel’s award memoire

1827 – Death of Fresnel by tuberculosis

1840 – Ernst Abbe born (1840 – 1905)

1849 – Stokes distribution of secondary waves

1850 – Fizeau and Foucault speed of light experiments

3. At Light Speed

There is no question that Francois Arago was a swashbuckler. His life’s story reads like an adventure novel as he went from being marooned in hostile lands early in his career to becoming prime minister of France after the 1848 revolutions swept across Europe.

Topics: The Birth of Interferometry. Snell’s Law. Fresnel and Arago. The First Interferometer. Fizeau and Foucault. The Speed of Light. Ether Drag. Jamin Interferometer.

1671 – Expedition to Hven by Picard and Rømer

1704 – Newton’s Opticks

1729 – James Bradley observation of stellar aberration

1784 – John Michel dark stars

1804 – Young wave theory of light and ether

1808 – Malus discovery of polarization of reflected light

1810 – Arago search for ether drag

1813 – Fraunhofer dark lines in Sun spectrum

1819 – Fresnel’s double mirror

1820 – Oersted discovers electromagnetism

1821 – Faraday electromagnetic phenomena

1821 – Fresnel light purely transverse

1823 – Fresnel reflection and refraction based on boundary conditions of ether

1827 – Green mathematical analysis of electricity and magnetism

GreenEssayGoogle Download

1830 – Cauchy ether as elastic solid

1831 – Faraday electromagnetic induction

1831 – Cauchy ether drag

1831 – Maxwell born

1831 – Faraday electromagnetic induction

1834 – Lloyd’s mirror

1836 – Cauchy’s second theory of the ether

1838 – Green theory of the ether

1839 – Hamilton group velocity

1839 – MacCullagh properties of rotational ether

1839 – Cauchy ether with negative compressibility

1841 – Maxwell entered Edinburgh Academy (age 10) met P. G. Tait

1842 – Doppler effect

DopplerFarbigeLicht-3 Download

1845 – Faraday effect (magneto-optic rotation)

1846 – Haidinger fringes

1846 – Stokes’ viscoelastic theory of the ether

1847 – Maxwell entered Edinburgh University

1848 – Fizeau proposal of the Fizeau-Doppler effect

1849 – Fizeau speed of light

1850 – Maxwell at Cambridge, studied under Hopkins, also knew Stokes and Whewell

1852 – Michelson born Strelno, Prussia

1854 – Maxwell wins the Smith’s Prize (Stokes’ theorem was one of the problems)

1855 – Michelson’s immigrate to San Francisco through Panama Canal

1855 – Maxwell “On Faraday’s Line of Force”

1856 – Jamin interferometer

1856 – Thomson magneto-optics effects (of Faraday)

1857 – Clausius constructs kinetic theory, Mean molecular speeds

Clausius (1857)_Nature motion we call heat Download

1859 – Fizeau light in moving medium

1862 – Fizeau fringes

1865 – Maxwell “A Dynamical Theory of the Electromagnetic Field”

1867 – Thomson and Tait “Treatise on Natural Philosophy”

1867 – Thomson hydrodynamic vortex atom

1868 – Fizeau proposal for stellar interferometry

1870 – Maxwell introduced “curl”, “convergence” and “gradient”

1871 – Maxwell appointed to Cambridge

1873 – Maxwell “A Treatise on Electricity and Magnetism”

4. After the Gold Rush

No name is more closely connected to interferometry than that of Albert Michelson. He succeeded, sometimes at great personal cost, in launching interferometric metrology as one of the most important tools used by scientists today.

Albert A. Michelson, 1907 Nobel Prize. Image Credit.

Topics: The Trials of Albert Michelson. Hermann von Helmholtz. Michelson and Morley. Fabry and Perot.

1810 – Arago search for ether drag

1813 – Fraunhofer dark lines in Sun spectrum

1813 – Faraday begins at Royal Institution

1820 – Oersted discovers electromagnetism

1821 – Faraday electromagnetic phenomena

1827 – Green mathematical analysis of electricity and magnetism

1830 – Cauchy ether as elastic solid

1831 – Faraday electromagnetic induction

1831 – Cauchy ether drag

1831 – Maxwell born

1831 – Faraday electromagnetic induction

1836 – Cauchy’s second theory of the ether

1838 – Green theory of the ether

1839 – Hamilton group velocity

1839 – MacCullagh properties of rotational ether

1839 – Cauchy ether with negative compressibility

1841 – Maxwell entered Edinburgh Academy (age 10) met P. G. Tait

1842 – Doppler effect

1845 – Faraday effect (magneto-optic rotation)

1846 – Stokes’ viscoelastic theory of the ether

1847 – Maxwell entered Edinburgh University

1850 – Maxwell at Cambridge, studied under Hopkins, also knew Stokes and Whewell

1852 – Michelson born Strelno, Prussia

1854 – Maxwell wins the Smith’s Prize (Stokes’ theorem was one of the problems)

1855 – Michelson’s immigrate to San Francisco through Panama Canal

1855 – Maxwell “On Faraday’s Line of Force”

1856 – Jamin interferometer

1856 – Thomson magneto-optics effects (of Faraday)

1859 – Fizeau light in moving medium

1859 – Discovery of the Comstock Lode

1860 – Maxwell publishes first paper on kinetic theory.

1861 – Maxwell “On Physical Lines of Force” speed of EM waves and molecular vortices, molecular vortex model

1862 – Michelson at boarding school in SF

1865 – Maxwell “A Dynamical Theory of the Electromagnetic Field”

1867 – Thomson and Tait “Treatise on Natural Philosophy”

1867 – Thomson hydrodynamic vortex atom

1868 – Fizeau proposal for stellar interferometry

1869 – Michelson meets US Grant and obtained appointment to Annapolis

1870 – Maxwell introduced “curl”, “convergence” and “gradient”

1871 – Maxwell appointed to Cambridge

1873 – Big Bonanza at the Consolidated Virginia mine

1873 – Maxwell “A Treatise on Electricity and Magnetism”

1873 – Michelson graduates from Annapolis

1875 – Michelson instructor at Annapolis

1877 – Michelson married Margaret Hemingway

1878 – Michelson First measurement of the speed of light with funds from father in law

1879 – Michelson Begin collaborating with Newcomb

1879 – Maxwell proposes second-order effect for ether drift experiments

1879 – Maxwell dies

1880 – Michelson Idea for second-order measurement of relative motion against ether

1880 – Michelson studies in Europe with Helmholtz in Berlin

1881 – Michelson Measurement at Potsdam with funds from Alexander Graham Bell

1882 – Michelson in Paris, Cornu, Mascart and Lippman

1882 – Michelson Joined Case School of Applied Science

1884 – Poynting energy flux vector

1885 – Michelson Began collaboration with Edward Morley of Western Reserve

1885 – Lorentz points out inconsistency of Stokes’ ether model

1885 – Fitzgerald wheel and band model, vortex sponge

1886 – Michelson and Morley repeat the Fizeau moving water experiment

Michelson1886 Download

1887 – Michelson Five days in July experiment on motion relative to ether

1887 – Michelson-Morley experiment published

MichelsonMorley1887 Download

1887 – Voigt derivation of relativistic Doppler (with coordinate transformations)

Voigt1887 Download

1888 – Hertz generation and detection of radio waves

1889 – Michelson moved to Clark University at Worcester

1889 – Fitzgerald contraction

1889 – Lodge cogwheel model of electromagnetism

1890 – Michelson Proposed use of interferometry in astronomy

1890 – Thomson devises a mechanical model of MacCullagh’s rotational ether

1890 – Hertz Galileo relativity and ether drag

1891 – Mach-Zehnder

1891 – Michelson measures diameter of Jupiter’s moons with interferometry

1891 – Thomson vortex electromagnetism

1892 – 1893 Michelson measurement of the Paris meter

1893 – Sirks interferometer

1893 – Michelson moved to University of Chicago to head Physics Dept.

1893 – Lorentz contraction

1894 – Lodge primitive radio demonstration

1895 – Marconi radio

1896 – Rayleigh’s interferometer

1897 – Lodge no ether drag on laboratory scale

1898 – Pringsheim interferometer

1899 – Fabry-Perot interferometer

1899 – Michelson remarried

1901 – 1903 Michelson President of the APS

1905 – Poincaré names the Lorentz transformations

1905 – Einstein’s special theory of Relativity

1907 – Michelson Nobel Prize

1913 – Sagnac interferometer

1916 – Twyman-Green interferometer

1920 – Stellar interferometer on the Hooker 100-inch telescope (Betelgeuse)

1923 – 1927 Michelson presided over the National Academy of Sciences

1931 – Michelson dies

5. Stellar Interference

Learning from his attempts to measure the speed of light through the ether, Michelson realized that the partial coherence of light from astronomical sources could be used to measure their sizes. His first measurements using the Michelson Stellar Interferometer launched a major subfield of astronomy that is one of the most active today.

Topics: Measuring the Stars. Astrometry. Moons of Jupiter. Schwarzschild. Betelgeuse. Michelson Stellar Interferometer. Banbury Brown Twiss. Sirius. Adaptive Optics.

1838 – Bessel stellar parallax measurement with Fraunhofer telescope

1868 – Fizeau proposes stellar interferometry

1873 – Stephan implements Fizeau’s stellar interferometer on Sirius, sees fringes

1880 – Michelson Idea for second-order measurement of relative motion against ether

1880 – 1882 Michelson Studies in Europe (Helmholtz in Berlin, Quincke in Heidelberg, Cornu, Mascart and Lippman in Paris)

1881 – Michelson Measurement at Potsdam with funds from Alexander Graham Bell

1881 – Michelson Resigned from active duty in the Navy

1883 – Michelson Joined Case School of Applied Science

1889 – Michelson moved to Clark University at Worcester

1890 – Michelson develops mathematics of stellar interferometry

1891 – Michelson measures diameters of Jupiter’s moons

Michelson1891 Download

1893 – Michelson moves to University of Chicago to head Physics Dept.

1896 – Schwarzschild double star interferometry

1907 – Michelson Nobel Prize

1908 – Hale uses Zeeman effect to measure sunspot magnetism

1910 – Taylor single-photon double slit experiment

1915 – Proxima Centauri discovered by Robert Innes

1916 – Einstein predicts gravitational waves

1920 – Stellar interferometer on the Hooker 100-inch telescope (Betelgeuse)

Michelson1921 Download

1947 – McCready sea interferometer observes rising sun (first fringes in radio astronomy

1952 – Ryle radio astronomy long baseline

1954 – Hanbury-Brown and Twiss radio intensity interferometry

1956 – Hanbury-Brown and Twiss optical intensity correlation, Sirius (optical)

1958 – Jennison closure phase

1970 – Labeyrie speckle interferometry

1974 – Long-baseline radio interferometry in practice using closure phase

1974 – Johnson, Betz and Townes: IR long baseline

1975 – Labeyrie optical long-baseline

1982 – Fringe measurements at 2.2 microns Di Benedetto

1985 – Baldwin closure phase at optical wavelengths

1991 – Coude du Foresto single-mode fibers with separated telescopes

1993 – Nobel prize to Hulse and Taylor for binary pulsar

1995 – Baldwin optical synthesis imaging with separated telescopes

1991 – Mayor and Queloz Doppler pull of 51 Pegasi

1999 – Upsilon Andromedae multiple planets

2009 – Kepler space telescope launched

2014 – Kepler announces 715 planets

2015 – Kepler-452b Earthlike planet in habitable zone

2015 – First detection of gravitational waves

2016 – Proxima Centauri b exoplanet confirmed

2017 – Nobel prize for gravitational waves

2018 – TESS (Transiting Exoplanet Survey Satellite)

2019 – Mayor and Queloz win Nobel prize for first exoplanet

2019 – First direct observation of exoplanet using interferometry

2019 – First image of a black hole obtained by very-long-baseline interferometry

6. Across the Universe

Stellar interferometry is opening new vistas of astronomy, exploring the wildest occupants of our universe, from colliding black holes half-way across the universe (LIGO) to images of neighboring black holes (EHT) to exoplanets near Earth that may harbor life.

Image of the supermassive black hole in M87 from Event Horizon Telescope.

Topics: Gravitational Waves, Black Holes and the Search for Exoplanets. Nulling Interferometer. Event Horizon Telescope. M87 Black Hole. Long Baseline Interferometry. LIGO.

1947 – Virgo A radio source identified as M87

1953 – Horace W. Babcock proposes adaptive optics (AO)

Babcock1953 Download

1958 – Jennison closure phase

1967 – First very long baseline radio interferometers (from meters to hundreds of km to thousands of km within a single year)

1967 – Ranier Weiss begins first prototype gravitational wave interferometer

1967 – Virgo X-1 x-ray source (M87 galaxy)

1970 – Poul Anderson’s Tau Zero alludes to AO in science fiction novel

1973 – DARPA launches adaptive optics research with contract to Itek, Inc.

1974 – Wyant (Itek) white-light shearing interferometer

1974 – Long-baseline radio interferometry in practice using closure phase

1975 – Hardy (Itek) patent for adaptive optical system

1975 – Weiss funded by NSF to develop interferometer for GW detection

1977 – Demonstration of AO on Sirius (Bell Labs and Berkeley)

1980 – Very Large Array (VLA) 6 mm to 4 meter wavelengths

1981 – Feinleib proposes atmospheric laser backscatter

1982 – Will Happer at Princeton proposes sodium guide star

1982 – Fringe measurements at 2.2 microns (Di Benedetto)

1983 – Sandia Optical Range demonstrates artificial guide star (Rayleigh)

1983 – Strategic Defense Initiative (Star Wars)

1984 – Lincoln labs sodium guide star demo

1984 – ESO plans AO for Very Large Telescope (VLT)

1985 – Laser guide star (Labeyrie)

1985 – Closure phase at optical wavelengths (Baldwin)

1988 – AFWL names Starfire Optical Range, Kirtland AFB outside Albuquerque

1988 – Air Force Maui Optical Site Schack-Hartmann and 241 actuators (Itek)

1988 – First funding for LIGO feasibility

1989 – 19-element-mirror Double star on 1.5m telescope in France

1989 – VLT approved for construction

1990 – Launch of the Hubble Space Telescope

1991 – Single-mode fibers with separated telescopes (Coude du Foresto)

1992 – ADONIS

1992 – NSF requests declassification of AO

1993 – VLBA (Very Long Baseline Array) 8,611 km baseline 3 mm to 90 cm

1994 – Declassification completed

1994 – Curvature sensor 3.6m Canada-France-Hawaii

1994 – LIGO funded by NSF, Barish becomes project director

1995 – Optical synthesis imaging with separated telescopes (Baldwin)

1995 – Doppler pull of 51 Pegasi (Mayor and Queloz)

1998 – ESO VLT first light

1998 – Keck installed with Schack-Hartmann

1999 – Upsilon Andromedae multiple planets

2000 – Hale 5m Palomar Schack-Hartmann

2001 – NAOS-VLT adaptive optics

2001 – VLTI first light (MIDI two units)

2002 – LIGO operation begins

2007 – VLT laser guide star

2007 – VLTI AMBER first scientific results (3 units)

2009 – Kepler space telescope launched

2009 – Event Horizon Telescope (EHT) project starts

2010 – Large Binocular Telescope (LBT) 672 actuators on secondary mirror

2010 – End of first LIGO run. No events detected. Begin Enhanced LIGO upgrade.

2011 – SPHERE-VLT 41×41 actuators (1681)

2012 – Extremely Large Telescope (ELT) approved for construction

2014 – Kepler announces 715 planets

2015 – Kepler-452b Earthlike planet in habitable zone

2015 – First detection of gravitational waves (LIGO)

2015 – LISA Pathfinder launched

2016 – Second detection at LIGO

2016 – Proxima Centauri b exoplanet confirmed

2016 – GRAVITY VLTI (4 units)

2017 – Nobel prize for gravitational waves

2018 – TESS (Transiting Exoplanet Survey Satellite) launched

2018 – MATTISE VLTI first light (combining all units)

2019 – Mayor and Queloz win Nobel prize

2019 – First direct observation of exoplanet using interferometry at LVTI

2019 – First image of a black hole obtained by very-long-baseline interferometry (EHT)

2020 – First neutron-star black-hole merger detected

2020 – KAGRA (Japan) online

2024 – LIGO India to go online

2025 – First light for ELT

2034 – Launch date for LISA

7. Two Faces of Microscopy

From the astronomically large dimensions of outer space to the microscopically small dimensions of inner space, optical interference pushes the resolution limits of imaging.

Topics: Diffraction and Interference. Joseph Fraunhofer. Diffraction Gratings. Henry Rowland. Carl Zeiss. Ernst Abbe. Phase-contrast Microscopy. Super-resolution Micrscopes. Structured Illumination.

1021 – Al Hazeni manuscript on Optics

1284 – First eye glasses by Salvino D’Armate

1590 – Janssen first microscope

1609 – Galileo first compound microscope

1625 – Giovanni Faber coins phrase “microscope”

1665 – Hook’s Micrographia

1676 – Antonie van Leeuwenhoek microscope

1787 – Fraunhofer born

1811 – Fraunhofer enters business partnership with Utzschneider

1816 – Carl Zeiss born

1821 – Fraunhofer first diffraction publication

1823 – Fraunhofer second diffraction publication 3200 lines per Paris inch

1830 – Spherical aberration compensated by Joseph Jackson Lister

1840 – Ernst Abbe born

1846 – Zeiss workshop in Jena, Germany

1850 – Fizeau and Foucault speed of light

1851 – Otto Schott born

1859 – Kirchhoff and Bunsen theory of emission and absorption spectra

1866 – Abbe becomes research director at Zeiss

1874 – Ernst Abbe equation on microscope resolution

1874 – Helmholtz image resolution equation

1880 – Rayleigh resolution

1888 – Hertz waves

1888 – Frits Zernike born

1925 – Zsigmondy Nobel Prize for light-sheet microscopy

1931 – Transmission electron microscope by Ruske and Knoll

1932 – Phase contrast microscope by Zernicke

1942 – Scanning electron microscope by Ruska

1949 – Mirau interferometric objective

1952 – Nomarski differential phase contrast microscope

1953 – Zernicke Nobel prize

1955 – First discussion of superresolution by Toraldo di Francia

1957 – Marvin Minsky patents confocal principle

1962 – Green flurescence protein (GFP) Shimomura, Johnson and Saiga

1966 – Structured illumination microscopy by Lukosz

1972 – CAT scan

1978 – Cremer confocal laser scanning microscope

1978 – Lohman interference microscopy

1981 – Binnig and Rohrer scanning tunneling microscope (STM)

1986 – Microscopy Nobel Prize: Ruska, Binnig and Rohrer

1990 – 4PI microscopy by Stefan Hell

1992 – GFP cloned

1993 – STED by Stefan Hell

1993 – Light sheet fluorescence microscopy by Spelman

1995 – Structured illumination microscopy by Guerra

1995 – Gustafsson image interference microscopy

1999 – Gustafsson I⁵M

2004 – Selective plane illumination microscopy (SPIM)

2006 – PALM and STORM (Betzig and Zhuang)

2014 – Nobel Prize (Hell, Betzig and Moerner)

8. Holographic Dreams of Princess Leia

The coherence of laser light is like a brilliant jewel that sparkles in the darkness, illuminating life, probing science and projecting holograms in virtual worlds.

Topics: Crossing Beams. Denis Gabor. Wavefront Reconstruction. Holography. Emmett Leith. Lasers. Ted Maiman. Charles Townes. Optical Maser. Dynamic Holography. Light-field Imaging.

1900 – Dennis Gabor born

1926 – Hans Busch magnetic electron lens

1927 – Gabor doctorate

1931 – Ruska and Knoll first two-stage electron microscope

1942 – Lawrence Bragg x-ray microscope

1948 – Gabor holography paper in Nature

1949 – Gabor moves to Imperial College

1950 – Lamb possibility of population inversion

1951 – Purcell and Pound demonstration of population inversion

1952 – Leith joins Willow Run Labs

1953 – Townes first MASER

1957 – SAR field trials

1957 – Gould coins LASER

1958 – Schawlow and Townes proposal for optical maser

1959 – Shawanga Lodge conference

1960 – Maiman first laser: pink ruby

1960 – Javan first gas laser: HeNe at 1.15 microns

1961 – Leith and Upatnieks wavefront reconstruction

1962 – HeNe laser in the visible at 632.8 nm

1962 – First laser holograms (Leith and Upatnieks)

1963 – van Heerden optical information storage

1963 – Leith and Upatnieks 3D holography

1966 – Ashkin optically-induced refractive index changes

1966 – Leith holographic information storage in 3D

1968 – Bell Labs holographic storage in Lithium Niobate and Tantalate

1969 – Kogelnik coupled wave theory for thick holograms

1969 – Electrical control of holograms in SBN

1970 – Optically induced refractive index changes in Barium Titanate

1971 – Amodei transport models of photorefractive effect

1971 – Gabor Nobel prize

1972 – Staebler multiple holograms

1974 – Glass and von der Linde photovoltaic and photorefractive effects, UV erase

1977 – Star Wars movie

1981 – Huignard two-wave mixing energy transfer

2012 – Coachella Music Festival

9. Photon Interference

What is the image of one photon interfering? Better yet, what is the image of two photons interfering? The answer to this crucial question laid the foundation for quantum communication.

Topics: The Beginnings of Quantum Communication. EPR paradox. Entanglement. David Bohm. John Bell. The Bell Inequalities. Leonard Mandel. Single-photon Interferometry. HOM Interferometer. Two-photon Fringes. Quantum cryptography. Quantum Teleportation.

1900 – Planck (1901). “Law of energy distribution in normal spectra.” [1]

Planck-1901-Annalen_der_Physik Download

1905 – A. Einstein (1905). “Generation and conversion of light wrt a heuristic point of view.” [2]

1909 – A. Einstein (1909). “On the current state of radiation problems.” [3]

1909 – Single photon double-slit experiment, G.I. Taylor [4]

1915 – Milliken photoelectric effect

1916 – Einstein predicts stimulated emission

1923 –Compton, Arthur H. (May 1923). Quantum Theory of the Scattering of X-Rays.[5]

1926 – Gilbert Lewis names “photon”

1926 – Dirac: photons interfere only with themselves

1927 – D. Dirac, P. A. M. (1927). Emission and absorption of radiation [6]

1932 – von Neumann textbook on quantum physics

1932 – E. P. Wigner: Phys. Rev. 40, 749 (1932)

1935 – EPR paper, A. Einstein, B. Podolsky, N. Rosen: Phys. Rev. 47 , 777 (1935)

1935 – Reply to EPR, N. Bohr: Phys. Rev. 48 , 696 (1935)

1935 – Schrödinger (1935 and 1936) on entanglement (cat?) “Present situation in QM”

1948 – Gabor holography

1950 – Wu correlated spin generation from particle decay

1951 – Bohm alternative form of EPR gedankenexperiment (quantum textbook)

1952 – Bohm nonlocal hidden variable theory[7]

1953 – Schwinger: Coherent states

1956 – Photon bunching, R. Hanbury-Brown, R.W. Twiss: Nature 177 , 27 (1956)

1957 – Bohm and Ahronov proof of entanglement in 1950 Wu experiment

1959 – Ahronov-Bohm effect of magnetic vector potential

1960 – Klauder: Coherent states

1963 – Coherent states, R. J. Glauber: Phys. Rev. 130 , 2529 (1963)

1963 – Coherent states, E. C. G. Sudarshan: Phys. Rev. Lett. 10, 277 (1963)

1964 – J. S. Bell: Bell inequalities [8]

1964 – Mandel professorship at Rochester

1967 – Interference at single photon level, R. F. Pfleegor, L. Mandel: [9]

1967 – M. O. Scully, W.E. Lamb: Phys. Rev. 159 , 208 (1967) Quantum theory of laser

1967 – Parametric converter (Mollow and Glauber) [10]

1967 – Kocher and Commins calcium 2-photon cascade

1969 – Quantum theory of laser, M. Lax, W.H. Louisell: Phys. Rev. 185 , 568 (1969)

1969 – CHSH inequality [11]

1972 – First test of Bell’s inequalities (Freedman and Clauser)

1975 – Carmichel and Walls predicted light in resonance fluorescence from a two-level atom would display photon anti-bunching (1976)

1977 – Photon antibunching in resonance fluorescence. H. J. Kimble, M. Dagenais and L. Mandel [12]

1978 – Kip Thorne quantum non-demolition (QND)

1979 – Hollenhorst squeezing for gravitational wave detection: names squeezing

1982 – Apect Experimental Bell experiments, [13]

1985 – Dick Slusher experimental squeezing

1985 – Deutsch quantum algorithm

1986 – Photon anti-bunching at a beamsplitter, P. Grangier, G. Roger, A. Aspect: [14]

1986 – Kimble squeezing in parametric down-conversion

1986 – C. K. Hong, L. Mandel: Phys. Rev. Lett. 56 , 58 (1986) one-photon localization

1987 – Two-photon interference (Ghosh and Mandel) [15]

1987 – HOM effect [16]

1987 – Photon squeezing, P. Grangier, R. E. Slusher, B. Yurke, A. La Porta: [17]

1987 – Grangier and Slusher, squeezed light interferometer

1988 – 2-photon Bell violation: Z. Y. Ou, L. Mandel: Phys. Rev. Lett. 61 , 50 (1988)

1988 – Brassard Quantum cryptography

1989 – Franson proposes two-photon interference in k-number (?)

1990 – Two-photon interference in k-number (Kwiat and Chiao)

1990 – Two-photon interference (Ou, Zhou, Wang and Mandel)

1993 – Quantum teleportation proposal (Bennett)

1994 – Teleportation of quantum states (Vaidman)

1994 – Shor factoring algorithm

1995 – Down-conversion for polarization: Kwiat and Zeilinger (1995)

1997 – Experimental quantum teleportation (Bouwmeester)

1997 – Experimental quantum teleportation (Bosci)

1998 – Unconditional quantum teleportation (every state) (Furusawa)

2001 – Quantum computing with linear optics (Knill, Laflamme, Milburn)

2013 – LIGO design proposal with squeezed light (Aasi)

2019 – Squeezing upgrade on LIGO (Tse)

2020 – Quantum computational advantage (Zhong)

10. The Quantum Advantage

There is almost no technical advantage better than having exponential resources at hand. The exponential resources of quantum interference provide that advantage to quantum computing which is poised to usher in a new era of quantum information science and technology.

Topics: Interferometric Computing. David Deutsch. Quantum Algorithm. Peter Shor. Prime Factorization. Quantum Logic Gates. Linear Optical Quantum Computing. Boson Sampling. Quantum Computational Advantage.

1980 – Paul Benioff describes possibility of quantum computer

1981 – Feynman simulating physics with computers

1985 – Deutsch quantum Turing machine [18]

1987 – Quantum properties of beam splitters

1992 – Deutsch Josza algorithm is exponential faster than classical

1993 – Quantum teleportation described

1994 – Shor factoring algorithm [19]

1994 – First quantum computing conference

1995 – Shor error correction

1995 – Universal gates

1996 – Grover search algorithm

1998 – First demonstration of quantum error correction

1999 – Nakamura and Tsai superconducting qubits

2001 – Superconducting nanowire photon detectors

2001 – Linear optics quantum computing (KLM)

2001 – One-way quantum computer

2003 – All-optical quantum gate in a quantum dot (Li)

2003 – All-optical quantum CNOT gate (O’Brien)

2003 – Decoherence and einselection (Zurek)

2004 – Teleportation across the Danube

2005 – Experimental quantum one-way computing (Walther)

2007 – Teleportation across 114 km (Canary Islands)

2008 – Quantum discord computing

2011 – D-Wave Systems offers commercial quantum computer

2011 – Aaronson boson sampling

2012 – 1QB Information Technnologies, first quantum software company

2013 – Experimental demonstrations of boson sampling

2014 – Teleportation on a chip

2015 – Universal linear optical quantum computing (Carolan)

2017 – Teleportation to a satellite

2019 – Generation of a 2D cluster state (Larsen)

2019 – Quantum supremacy [20]

2020 – Quantum optical advantage [21]

2021 – Programmable quantum photonic chip

By David D. Nolte, Nov. 9, 2023

References:

[1] Annalen Der Physik 4(3): 553-563.

[2] Annalen Der Physik 17(6): 132-148.

[3] Physikalische Zeitschrift 10: 185-193.

[4] Proc. Cam. Phil. Soc. Math. Phys. Sci. 15 , 114 (1909)

[5] Physical Review. 21 (5): 483–502.

[6] Proceedings of the Royal Society of London Series a-Containing Papers of a Mathematical and Physical Character 114(767): 243-265.

[7] D. Bohm, “A suggested interpretation of the quantum theory in terms of hidden variables .1,” Physical Review, vol. 85, no. 2, pp. 166-179, (1952)

[8] Physics 1 , 195 (1964); Rev. Mod. Phys. 38 , 447 (1966)

[9] Phys. Rev. 159 , 1084 (1967)

[10] B. R. Mollow, R. J. Glauber: Phys. Rev. 160, 1097 (1967); 162, 1256 (1967)

[11] J. F. Clauser, M. A. Horne, A. Shimony, and R. A. Holt, ” Proposed experiment to test local hidden-variable theories,” Physical Review Letters, vol. 23, no. 15, pp. 880-&, (1969)

[12] (1977) Phys. Rev. Lett. 39, 691-5

[13] A. Aspect, P. Grangier, G. Roger: Phys. Rev. Lett. 49 , 91 (1982). A. Aspect, J. Dalibard, G. Roger: Phys. Rev. Lett. 49 , 1804 (1982)

[14] Europhys. Lett. 1 , 173 (1986)

[15] R. Ghosh and L. Mandel, “Observation of nonclassical effects in the interference of 2 photons,” Physical Review Letters, vol. 59, no. 17, pp. 1903-1905, Oct (1987)

[16] C. K. Hong, Z. Y. Ou, and L. Mandel, “Measurement of subpicosecond time intervals between 2 photons by interference,” Physical Review Letters, vol. 59, no. 18, pp. 2044-2046, Nov (1987)

[17] Phys. Rev. Lett 59, 2153 (1987)

[18] D. Deutsch, “QUANTUM-THEORY, THE CHURCH-TURING PRINCIPLE AND THE UNIVERSAL QUANTUM COMPUTER,” Proceedings of the Royal Society of London Series a-Mathematical Physical and Engineering Sciences, vol. 400, no. 1818, pp. 97-117, (1985)

[19] P. W. Shor, “ALGORITHMS FOR QUANTUM COMPUTATION – DISCRETE LOGARITHMS AND FACTORING,” in 35th Annual Symposium on Foundations of Computer Science, Proceedings, S. Goldwasser Ed., (Annual Symposium on Foundations of Computer Science, 1994, pp. 124-134.

[20] F. Arute et al., “Quantum supremacy using a programmable superconducting processor,” Nature, vol. 574, no. 7779, pp. 505-+, Oct 24 (2019)

[21] H.-S. Zhong et al., “Quantum computational advantage using photons,” Science, vol. 370, no. 6523, p. 1460, (2020)

Relativistic Velocity Addition: Einstein’s Crucial Insight

The first step on the road to Einstein’s relativity was taken a hundred years earlier by an ironic rebel of physics—Augustin Fresnel. His radical (at the time) wave theory of light was so successful, especially the proof that it must be composed of transverse waves, that he was single-handedly responsible for creating the irksome luminiferous aether that would haunt physicists for the next century. It was only when Einstein combined the work of Fresnel with that of Hippolyte Fizeau that the aether was ultimately banished.

Augustin Fresnel: Ironic Rebel of Physics

Augustin Fresnel was an odd genius who struggled to find his place in the technical hierarchies of France. After graduating from the Ecole Polytechnique, Fresnel was assigned a mindless job overseeing the building of roads and bridges in the boondocks of France—work he hated. To keep himself from going mad, he toyed with physics in his spare time, and he stumbled on inconsistencies in Newton’s particulate theory of light that Laplace, a leader of the French scientific community, embraced as if it were revealed truth .

The final irony is that Einstein used Fresnel’s theoretical coefficient and Fizeau’s measurements—that had introduced aether drag in the first place—to show that there was no aether.

Fresnel rebelled, realizing that effects of diffraction could be explained if light were made of waves. He wrote up an initial outline of his new wave theory of light, but he could get no one to listen, until Francois Arago heard of it. Arago was having his own doubts about the particle theory of light based on his experiments on stellar aberration.

*Augustin Fresnel and Francois Arago (circa 1818*)

Stellar Aberration and the Fresnel Drag Coefficient

Stellar aberration had been explained by James Bradley in 1729 as the effect of the motion of the Earth relative to the motion of light “particles” coming from a star. The Earth’s motion made it look like the star was tilted at a very small angle (see my previous blog). That explanation had worked fine for nearly a hundred years, but then around 1810 Francois Arago at the Paris Observatory made extremely precise measurements of stellar aberration while placing finely ground glass prisms in front of his telescope. According to Snell’s law of refraction, which depended on the velocity of the light particles, the refraction angle should have been different at different times of the year when the Earth was moving one way or another relative to the speed of the light particles. But to high precision the effect was absent. Arago began to question the particle theory of light. When he heard about Fresnel’s work on the wave theory, he arranged a meeting, encouraging Fresnel to continue his work.

But at just this moment, in March of 1815, Napoleon returned from exile in Elba and began his march on Paris with a swelling army of soldiers who flocked to him. Fresnel rebelled again, joining a royalist militia to oppose Napoleon’s return. Napoleon won, but so did Fresnel, who was ironically placed under house arrest, which was like heaven to him. It freed him from building roads and bridges, giving him free time to do optics experiments in his mother’s house to support his growing theoretical work on the wave nature of light.

Arago convinced the authorities to allow Fresnel to come to Paris, where the two began experiments on diffraction and interference. By using polarizers to control the polarization of the interfering light paths, they concluded that light must be composed of transverse waves.

This brilliant insight was then followed by one of the great tragedies of science—waves needed a medium within which to propagate, so Fresnel conceived of the luminiferous aether to support it. Worse, the transverse properties of light required the aether to have a form of crystalline stiffness.

How could moving objects, like the Earth orbiting the sun, travel through such an aether without resistance? This was a serious problem for physics. One solution was that the aether was entrained by matter, so that as matter moved, the aether was dragged along with it. That solved the resistance problem, but it raised others, because it couldn’t explain Arago’s refraction measurements of aberration.

Fresnel realized that Arago’s null results could be explained if aether was only partially dragged along by matter. For instance, in the glass prisms used by Arago, the fraction of the aether being dragged along by the moving glass versus at rest would depend on the refractive index n of the glass. The speed of light in moving glass would then be

where c is the speed of light through stationary aether, v_g is the speed of the glass prism through the stationary aether, and V is the speed of light in the moving glass. The first term in the expression is the ordinary definition of the speed of light in stationary matter with the refractive index. The second term is called the Fresnel drag coefficient which he communicated to Arago in a letter in 1818. Even at the high speed of the Earth moving around the sun, this second term is a correction of only about one part in ten thousand. It explained Arago’s null results for stellar aberration, but it was not possible to measure it directly in the laboratory at that time.

Fizeau’s Moving Water Experiment

Hippolyte Fizeau has the distinction of being the first to measure the speed of light directly in an Earth-bound experiment. All previous measurements had been astronomical. The story of his ingenious use of a chopper wheel and long-distance reflecting mirrors placed across the city of Paris in 1849 can be found in Chapter 3 of Interference. However, two years later he completed an experiment that few at the time noticed but which had a much more profound impact on the history of physics.

In 1851, Fizeau modified an Arago interferometer to pass two interfering light beams along pipes of moving water. The goal of the experiment was to measure the aether drag coefficient directly and to test Fresnel’s theory of partial aether drag. The interferometer allowed Fizeau to measure the speed of light in moving water relative to the speed of light in stationary water. The results of the experiment confirmed Fresnel’s drag coefficient to high accuracy, which seemed to confirm the partial drag of aether by moving matter.

*Fizeau’s 1851 measurement of the speed of light in water using a modified Arago interferometer.* (Reprinted from Chapter 2: Interference.)

This result stood for thirty years, presenting its own challenges for physicist exploring theories of the aether. The sophistication of interferometry improved over that time, and in 1881 Albert Michelson used his newly-invented interferometer to measure the speed of the Earth through the aether. He performed the experiment in the Potsdam Observatory outside Berlin, Germany, and found the opposite result of complete aether drag, contradicting Fizeau’s experiment. Later, after he began collaborating with Edwin Morley at Case and Western Reserve Colleges in Cleveland, Ohio, the two repeated Fizeau’s experiment to even better precision, finding once again Fresnel’s drag coefficient, followed by their own experiment, known now as “the Michelson-Morley Experiment” in 1887, that found no effect of the Earth’s movement through the aether.

The two experiments—Fizeau’s measurement of the Fresnel drag coefficient, and Michelson’s null measurement of the Earth’s motion—were in direct contradiction with each other. Based on the theory of the aether, they could not both be true.

But where to go from there? For the next 15 years, there were numerous attempts to put bandages on the aether theory, from Fitzgerald’s contraction to Lorenz’ transformations, but it all seemed like kludges built on top of kludges. None of it was elegant—until Einstein had his crucial insight.

Einstein’s Insight

While all the other top physicists at the time were trying to save the aether, taking its real existence as a fact of Nature to be reconciled with experiment, Einstein took the opposite approach—he assumed that the aether did not exist and began looking for what the experimental consequences would be.

From the days of Galileo, it was known that measured speeds depended on the frame of reference. This is why a knife dropped by a sailor climbing the mast of a moving ship strikes at the base of the mast, falling in a straight line in the sailor’s frame of reference, but an observer on the shore sees the knife making an arc—velocities of relative motion must add. But physicists had over-generalized this result and tried to apply it to light—Arago, Fresnel, Fizeau, Michelson, Lorenz—they were all locked in a mindset.

Einstein stepped outside that mindset and asked what would happen if all relatively moving observers measured the same value for the speed of light, regardless of their relative motion. It was just a little algebra to find that the way to add the speed of light c to the speed of a moving reference frame v_ref was

where the numerator was the usual Galilean relativity velocity addition, and the denominator was required to enforce the constancy of observed light speeds. Therefore, adding the speed of light to the speed of a moving reference frame gives back simply the speed of light.

Generalizing this equation for general velocity addition between moving frames gives

where u is now the speed of some moving object being added the the speed of a reference frame, and v_obs is the “net” speed observed by some “external” observer . This is Einstein’s famous equation for relativistic velocity addition (see pg. 12 of the English translation). It ensures that all observers with differently moving frames all measure the same speed of light, while also predicting that no velocities for objects can ever exceed the speed of light.

This last fact is a consequence, not an assumption, as can be seen by letting the reference speed v_ref increase towards the speed of light so that v_ref ≈ c, then

so that the speed of an object launched in the forward direction from a reference frame moving near the speed of light is still observed to be no faster than the speed of light

All of this, so far, is theoretical. Einstein then looked to find some experimental verification of his new theory of relativistic velocity addition, and he thought of the Fizeau experimental measurement of the speed of light in moving water. Applying his new velocity addition formula to the Fizeau experiment, he set v_ref = v_water and u = c/n and found

The second term in the denominator is much smaller that unity and is expanded in a Taylor’s expansion

The last line is exactly the Fresnel drag coefficient!

Therefore, Fizeau, half a century before, in 1851, had already provided experimental verification of Einstein’s new theory for relativistic velocity addition! It wasn’t aether drag at all—it was relativistic velocity addition.

From this point onward, Einstein followed consequence after inexorable consequence, constructing what is now called his theory of Special Relativity, complete with relativistic transformations of time and space and energy and matter—all following from a simple postulate of the constancy of the speed of light and the prescription for the addition of velocities.

The final irony is that Einstein used Fresnel’s theoretical coefficient and Fizeau’s measurements, that had established aether drag in the first place, as the proof he needed to show that there was no aether. It was all just how you looked at it.

By David D. Nolte, Oct. 18, 2023

The Aberration of Starlight: Relativity’s Crucible

The Earth races around the sun with remarkable speed—at over one hundred thousand kilometers per hour on its yearly track. This is about 0.01% of the speed of light—a small but non-negligible amount for which careful measurement might show the very first evidence of relativistic effects. How big is this effect and how do you measure it? One answer is the aberration of starlight, which is the slight deviation in the apparent position of stars caused by the linear speed of the Earth around the sun.

This is not parallax, which is caused the the changing position of the Earth around the sun. Ever since Copernicus, astronomers had been searching for parallax, which would give some indication how far away stars were. It was an important question, because the answer would say something about how big the universe was. But in the process of looking for parallax, astronomers found something else, something about 50 times bigger—aberration.

Aberration is the effect of the transverse speed of the Earth added to the speed of light coming from a star. For instance, this effect on the apparent location of stars in the sky is a simple calculation of the arctangent of 0.01%, which is an angle of about 20 seconds of arc, or about 40 seconds when comparing two angles 6 months apart. This was a bit bigger than the accuracy of astronomical measurements at the time when Jean Picard travelled from Paris to Denmark in 1671 to visit the ruins of the old observatory of Tycho Brahe at Uranibourg.

Fig. 1 Stellar parallax is the change in apparent positions of a star caused by the change in the Earth’s position as it orbits the sun. If the change in angle (θ) could be measured, then based on Newton’s theory of gravitation that gives the radius of the Earth’s orbit (R), the distance to the star (L) could be found.

Jean Picard at Uranibourg

*Fig. 2 A view of Tycho Brahe’s Uranibourg astronomical observatory in Hven, Denmark. Tycho had to abandon it near the end of his life when a new king thought he was performing witchcraft.*

Jean Picard went to Uranibourg originally in 1671, and during subsequent years, to measure the eclipses of the moons of Jupiter to determine longitude at sea—an idea first proposed by Galileo. When visiting Copenhagen, before heading out to the old observatory, Picard secured the services of an as yet unknown astronomer by the name of Ole Rømer. While at Uranibourg, Picard and Rømer made their required measurements of the eclipses of the moons of Jupiter, but with extra observation hours, Picard also made measurements of the positions of selected stars, such as Polaris, the North Star. His very precise measurements allowed him to track a tiny yearly shift, an aberration, in position by about 40 seconds of arc. At the time (before Rømer’s great insight about the finite speed of light—see Chapter 1 of Interference (Oxford, 2023)), the speed of light was thought to be either infinite or unmeasurably fast, so Picard thought that this shift was the long-sought effect of stellar parallax that would serve as a way to measure the distance to the stars. However, the direction of the shift of Polaris was completely wrong if it were caused by parallax, and Picard’s stellar aberration remained a mystery.

*Fig. 3 Jean Picard (left) and his modern name-sake (right).*

Samuel Molyneux and Murder in Kew

In 1725, the amateur Irish astronomer Samuel Molyneux (1689 – 1828) decided that the tools of astronomy had improved to the point that the question of parallax could be answered. He enlisted the help of an instrument maker outside London to install a 24-foot zenith sector (a telescope that points vertically upwards) at his home in Kew. Molyneux was an independently wealthy politician (he had married the first daughter of the second Earl of Essex) who sat in the British House of Commons, and he was also secretary to the Prince of Wales (the future George II). Because his political activities made demands on his time, he looked for assistance with his observations and invited James Bradley (1693 – 1762), the newly installed Savilian Professor of Astronomy at Oxford University, to join him in his search.

James Bradley was a rising star in the scientific circles of England. He came from a modest background but had the good fortune that his mother’s brother, James Pound, was a noted amateur astronomer who had set up a small observatory at his rectory in Wanstead. Bradley showed an early interest in astronomy, and Pound encouraged him, helping with the finances of his education that took him to degrees at Baliol College at Oxford. Even more fortunate was the fact that Pound’s close friend was the Astronomer Royal Edmund Halley, who also took a special interest in Bradley. With Halley’s encouragement, Bradley made important measurements of Mars and several nebulae, demonstrating an ability to work with great accuracy. Halley was impressed and nominated Bradley to the Royal Society in 1718, telling everyone that Bradley was destined to be one of the great astronomers of his time.

Molyneux must have sensed immediately that he had chosen wisely by selecting Bradley to help him with the parallax measurements. Bradley was capable of exceedingly precise work and was fluent mathematically with the geometric complexities of celestial orbits. Fastening the large zenith sector to the chimney of the house gave the apparatus great stability, and in December of 1725 they commenced observations of Gamma Draconis as it passed directly overhead. Because of the accuracy of the sector, they quickly observed a deviation in the star’s position, but the deviation was in the wrong direction, just as Picard had observed. They continued to make observations over two years, obtaining a detailed map of a yearly wobble in the star’s position as it changed angle by 40 seconds of arc (about one percent of a degree) over six months.

When Molyneux was appointed Lord of the Admiralty in 1727, as well as becoming a member of the Irish Parliament (representing Dublin University), he had little time to continue with the observations of Gamma Draconis. He helped Bradley set up a Zenith sector telescope at Bradley’s uncle’s observatory in Wanstead that had a wider field of view to observe more stars, and then he left the project to his friend. A few months later, before either he or Bradley had understood the cause of the stellar aberration, Molyneux collapsed while in the House of Commons and was carried back to his house. One of Molyneux’s many friends was the court anatomist Nathaniel St. André who attended to him over the next several days as he declined and died. St. André was already notorious for roles he had played in several public hoaxes, and on the night of his friend’s death, before the body had grown cold, he eloped with Molyneux’s wife, raising accusations of murder (that could never be proven).

James Bradley and the Light Wind

Over the following year, Bradley observed aberrations in several stars, all of them displaying the same yearly wobble of about 40 seconds of arc. This common behavior of numerous stars demanded a common explanation, something they all shared. It is said that the answer came to Bradley while he was boating on the Thames. The story may be apocryphal, but he apparently noticed the banner fluttering downwind at the top of the mast, and after the boat came about, the banner pointed in a new direction. The wind direction itself had not altered, but the motion of the boat relative to the wind had changed. Light at that time was considered to be made of a flux of corpuscles, like a gentle wind of particles. As the Earth orbited the Sun, its motion relative to this wind would change periodically with the seasons, and the apparent direction of the star would shift a little as a result.

Fig. 5 Principle of stellar aberration. On the left is the rest frame of the star positioned directly overhead as a moving telescope tube must be slightly tilted at an angle (equal to the arctangent of the ratio of the Earth’s speed to the speed of light–greatly exaggerated in the figure) to allow the light to pass through it. On the right is the rest frame of the telescope in which the angular position of the star appears shifted.

Bradley shared his observations and his explanation in a letter to Halley that was read before the Royal Society in January of 1729. Based on his observations, he calculated the speed of light to be about ten thousand times faster than the speed of the Earth in its orbit around the Sun. At that speed, it should take light eight minutes and twelve seconds to travel from the Sun to the Earth (the actual number is eight minutes and 19 seconds). This number was accurate to within a percent of the true value compared with the estimates made by Huygens from the eclipses of the moons of Jupiter that were in error by 27 percent. In addition, because he was unable to discern any effect of parallax in the stellar motions, Bradley was able to place a limit on how far the distant stars must be, more than 100,000 times farther the distance of the Earth from the Sun, which was much farther away than any had previously expected. In January of 1729 the size of the universe suddenly jumped to an incomprehensibly large scale.

Bradley’s explanation of the aberration of starlight was simple and matched observations with good quantitative accuracy. The particle nature of light made it like a wind, or a current, and the motion of the Earth was just a case of Galilean relativity that any freshman physics student can calculate. At first there seemed to be no controversy or difficulties with this interpretation. However, an obscure paper published in 1784 by an obscure English natural philosopher named John Michell (the first person to conceive of a “dark star”) opened a Pandora’s box that launched the crisis of the luminiferous ether and the eventual triumph of Einstein’s theory of Relativity (see Chapter 3 of Interference (Oxford, 2023)), .

By David D. Nolte, Sept. 27, 2023

July 26, 2023August 16, 2025 by David D. Nolte

Book Preview: Interference. The History of Optical Interferometry

This history of interferometry has many surprising back stories surrounding the scientists who discovered and explored one of the most important aspects of the physics of light—interference. From Thomas Young who first proposed the law of interference, and Augustin Fresnel and Francois Arago who explored its properties, to Albert Michelson, who went almost mad grappling with literal firestorms surrounding his work, these scientists overcame personal and professional obstacles on their quest to uncover light’s secrets. The book’s stories, told around the topic of optics, tells us something more general about human endeavor as scientists pursue science.

Interference: The History of Optical Interferometry and the Scientists who Tamed Light, was published Ag. 6 and is available at Oxford University Press and Amazon. Here is a brief preview of the frist several chapters:

Chapter 1. Thomas Young Polymath: The Law of Interference

The chapter, Thomas Young Polymath: The Law of Interference, begins with the story of the invasion of Egypt in 1798 by Napoleon Bonaparte as the unlikely link among a set of epic discoveries that launched the modern science of light. The story of interferometry passes from the Egyptian campaign and the discovery of the Rosetta Stone to Thomas Young. Young was a polymath, known for his facility with languages that helped him decipher Egyptian hieroglyphics aided by the Rosetta Stone. He was also a city doctor who advised the admiralty on the construction of ships, and he became England’s premier physicist at the beginning of the nineteenth century, building on the wave theory of Huygens, as he challenged Newton’s particles of light. But his theory of the wave nature of light was controversial, attracting sharp criticism that would pass on the task of refuting Newton to a new generation of French optical physicists.

Chapter 2. The Fresnel Connection: Particles versus Waves

Augustin Fresnel was an intuitive genius whose talents were almost squandered on his job building roads and bridges in the backwaters of France until he was discovered and rescued by Francois Arago.

The Fresnel Connection: Particles versus Waves describes the campaign of Arago and Fresnel to prove the wave nature of light based on Fresnel’s theory of interfering waves in diffraction. Although the discovery of the polarization of light by Etienne Malus posed a stark challenge to the undulationists, the application of wave interference, with the superposition principle of Daniel Bernoulli, provided the theoretical framework for the ultimate success of the wave theory. The final proof came through the dramatic demonstration of the Spot of Arago.

Chapter 3. At Light Speed: The Birth of Interferometry

At Light Speed: The Birth of Interferometry tells how Arago attempted to use Snell’s Law to measure the effect of the Earth’s motion through space but found no effect, in contradiction to predictions using Newton’s particle theory of light. Direct measurements of the speed of light were made by Hippolyte Fizeau and Leon Foucault who originally began as collaborators but had an epic falling-out that turned into an intense competition. Fizeau won priority for the first measurement, but Foucault surpassed him by using the Arago interferometer to measure the speed of light in air and water with increasing accuracy. Jules Jamin later invented one of the first interferometric instruments for use as a refractometer.

Chapter 4. After the Gold Rush: The Trials of Albert Michelson

After the Gold Rush: The Trials of Albert Michelson tells the story of Michelson’s youth growing up in the gold fields of California before he was granted an extraordinary appointment to Annapolis by President Grant. Michelson invented his interferometer while visiting Hermann von Helmholtz in Berlin, Germany, as he sought to detect the motion of the Earth through the luminiferous ether, but no motion was detected. After returning to the States and a faculty position at Case University, he met Edward Morley, and the two continued the search for the Earth’s motion, concluding definitively its absence. The Michelson interferometer launched a menagerie of interferometers (including the Fabry-Perot interferometer) that ushered in the golden age of interferometry.

Chapter 5. Stellar Interference: Measuring the Stars

Stellar Interference: Measuring the Stars brings the story of interferometry to the stars as Michelson proposed stellar interferometry, first demonstrated on the Galilean moons of Jupiter, followed by an application developed by Karl Schwarzschild for binary stars, and completed by Michelson with observations encouraged by George Hale on the star Betelgeuse. However, the Michelson stellar interferometry had stability limitations that were overcome by Hanbury Brown and Richard Twiss who developed intensity interferometry based on the effect of photon bunching. The ultimate resolution of telescopes was achieved after the development of adaptive optics that used interferometry to compensate for atmospheric turbulence.

And More

The last 5 chapters bring the story from Michelson’s first stellar interferometer into the present as interferometry is used today to search for exoplanets, to image distant black holes half-way across the universe and to detect gravitational waves using the most sensitive scientific measurement apparatus ever devised.

Chapter 6. Across the Universe: Exoplanets, Black Holes and Gravitational Waves

Moving beyond the measurement of star sizes, interferometry lies at the heart of some of the most dramatic recent advances in astronomy, including the detection of gravitational waves by LIGO, the imaging of distant black holes and the detection of nearby exoplanets that may one day be visited by unmanned probes sent from Earth.

Chapter 7. Two Faces of Microscopy: Diffraction and Interference

The complement of the telescope is the microscope. Interference microscopy allows invisible things to become visible and for fundamental limits on image resolution to be blown past with super-resolution at the nanoscale, revealing the intricate workings of biological systems with unprecedented detail.

Chapter 8. Holographic Dreams of Princess Leia: Crossing Beams

Holography is the direct legacy of Young’s double slit experiment, as coherent sources of light interfere to record, and then reconstruct, the direct scattered fields from illuminated objects. Holographic display technology promises to revolutionize virtual reality.

Chapter 9. Photon Interference: The Foundations of Quantum Communication and Computing

Quantum information science, at the forefront of physics and technology today, owes much of its power to the principle of interference among single photons.

Chapter 10. The Quantum Advantage: Interferometric Computing

Photonic quantum systems have the potential to usher in a new information age using interference in photonic integrated circuits.

A popular account of the trials and toils of the scientists and engineers who tamed light and used it to probe the universe.

Available at Amazon

and at Oxford University Press

and at Barnes & Noble

Arago and the first interferometer with Fresnel

March 22, 2023August 16, 2025 by David D. Nolte

Francois Arago and the Birth of Optical Science

An excerpt from the upcoming book “Interference: The History of Optical Interferometry and the Scientists who Tamed Light” describes how a handful of 19^th-century scientists laid the groundwork for one of the key tools of modern optics. Published in Optics and Photonics News, March 2023.

François Arago rose to the highest levels of French science and politics. Along the way, he met Augustin Fresnel and, together, they changed the course of optical science.

Link to OPN Article

New from Oxford Press: The History of Light and Interference (2023)

A popular account of the trials and toils of the scientists and engineers who tamed light and used it to probe the universe.

Available at Amazon

and at Oxford University Press

and at Barnes & Noble

May 8, 2022August 16, 2025 by David D. Nolte

The Many Worlds of the Quantum Beam Splitter

In one interpretation of quantum physics, when you snap your fingers, the trajectory you are riding through reality fragments into a cascade of alternative universes—one for each possible quantum outcome among all the different quantum states composing the molecules of your fingers.

This is the Many-Worlds Interpretation (MWI) of quantum physics first proposed rigorously by Hugh Everett in his doctoral thesis in 1957 under the supervision of John Wheeler at Princeton University. Everett had been drawn to this interpretation when he found inconsistencies between quantum physics and gravitation—topics which were supposed to have been his actual thesis topic. But his side-trip into quantum philosophy turned out to be a one-way trip. The reception of his theory was so hostile, no less than from Copenhagen and Bohr himself, that Everett left physics and spent a career at the Pentagon.

Resurrecting MWI in the Name of Quantum Information

Fast forward by 20 years, after Wheeler had left Princeton for the University of Texas at Austin, and once again a young physicist was struggling to reconcile quantum physics with gravity. Once again the many worlds interpretation of quantum physics seemed the only sane way out of the dilemma, and once again a side-trip became a life-long obsession.

David Deutsch, visiting Wheeler in the early 1980’s, became convinced that the many worlds interpretation of quantum physics held the key to paradoxes in the theory of quantum information (For the full story of Wheeler, Everett and Deutsch, see Ref [1]). He was so convinced, that he began a quest to find a physical system that operated on more information than could be present in one universe at a time. If such a physical system existed, it would be because streams of information from more than one universe were coming together and combining in a way that allowed one of the universes to “borrow” the information from the other.

It took only a year or two before Deutsch found what he was looking for—a simple quantum algorithm that yielded twice as much information as would be possible if there were no parallel universes. This is the now-famous Deutsch algorithm—the first quantum algorithm [2]. At the heart of the Deutsch algorithm is a simple quantum interference. The algorithm did nothing useful—but it convinced Deutsch that two universes were interfering coherently in the measurement process, giving that extra bit of information that should not have been there otherwise. A few years later, the Deutsch-Josza algorithm [2] expanded the argument to interfere an exponentially larger amount of information streams from an exponentially larger number of universes to create a result that was exponentially larger than any classical computer could produce. This marked the beginning of the quest for the quantum computer that is running red-hot today.

Deutsch’s “proof” of the many-worlds interpretation of quantum mechanics is not a mathematical proof but is rather a philosophical proof. It holds no sway over how physicists do the math to make their predictions. The Copenhagen interpretation, with its “spooky” instantaneous wavefunction collapse, works just fine predicting the outcome of quantum algorithms and the exponential quantum advantage of quantum computing. Therefore, the story of David Deutsch and the MWI may seem like a chimera—except for one fact—it inspired him to generate the first quantum algorithm that launched what may be the next revolution in the information revolution of modern society. Inspiration is important in science, because it lets scientists create things that had been impossible before.

But if quantum interference is the heart of quantum computing, then there is one physical system that has the ultimate simplicity that may yet inspire future generations of physicists to invent future impossible things—the quantum beam splitter. Nothing in the study of quantum interference can be simpler than a sliver of dielectric material sending single photons one way or another. Yet the outcome of this simple system challenges the mind and reminds us of why Everett and Deutsch embraced the MWI in the first place.

The Classical Beam Splitter

The so-called “beam splitter” is actually a misnomer. Its name implies that it takes a light beam and splits it into two, as if there is only one input. But every “beam splitter” has two inputs, which is clear by looking at the classical 50/50 beam splitter. The actual action of the optical element is the combination of beams into superpositions in each of the outputs. It is only when one of the input fields is zero, a special case, that the optical element acts as a beam splitter. In general, it is a beam combiner.

Given two input fields, the output fields are superpositions of the inputs

The square-root of two factor ensures that energy is conserved, because optical fluence is the square of the fields. This relation is expressed more succinctly as a matrix input-output relation

The phase factors in these equations ensure that the matrix is unitary

reflecting energy conservation.

The Quantum Beam Splitter

A quantum beam splitter is just a classical beam splitter operating at the level of individual photons. Rather than describing single photons entering or leaving the beam splitter, it is more practical to describe the properties of the fields through single-photon quantum operators

where the unitary matrix is the same as the classical case, but with fields replaced by the famous “a” operators. The photon operators operate on single photon modes. For instance, the two one-photon input cases are

where the creation operators operate on the vacuum state in each of the input modes.

The fundamental combinational properties of the beam splitter are even more evident in the quantum case, because there is no such thing as a single input to a quantum beam splitter. Even if no photons are directed into one of the input ports, that port still receives a “vacuum” input, and this vacuum input contributes to the fluctuations observed in the outputs.

The input-output relations for the quantum beam splitter are

The beam splitter operating on a one-photon input converts the input-mode creation operator into a superposition of out-mode creation operators that generates

The resulting output is entangled: either the single photon exits one port, or it exits the other. In the many worlds interpretation, the photon exits from one port in one universe, and it exits from the other port in a different universe. On the other hand, in the Copenhagen interpretation, the two output ports of the beam splitter are perfectly anti-correlated.

Fig. 1 Quantum Operations of a Beam Splitter. A beam splitter creates a quantum superposition of the input modes. The a-symbols are quantum number operators that create and annihilate photons. A single-photon input produces an entangled output that is a quantum superposition of the photon coming out of one output or the other.

The Hong-Ou-Mandel (HOM) Interferometer

When more than one photon is incident on a beam splitter, the fascinating effects of quantum interference come into play, creating unexpected outputs for simple inputs. For instance, the simplest example is a two photon input where a single photon is present in each input port of the beam splitter. The input state is represented with single creation operators operating on each vacuum state of each input port

creating a single photon in each of the input ports. The beam splitter operates on this input state by converting the input-mode creation operators into out-put mode creation operators to give

The important step in this process is the middle line of the equations: There is perfect destructive interference between the two single-photon operations. Therefore, both photons always exit the beam splitter from the same port—never split. Furthermore, the output is an entangled two-photon state, once more splitting universes.

Fig. 2 The HOM interferometer. A two-photon input on a beam splitter generates an entangled superposition of the two photons exiting the beam splitter always together.

The two-photon interference experiment was performed in 1987 by Chung Ki Hong and Jeff Ou, students of Leonard Mandel at the Optics Institute at the University of Rochester [4], and this two-photon operation of the beam splitter is now called the HOM interferometer. The HOM interferometer has become a center-piece for optical and photonic implementations of quantum information processing and quantum computers.

N-Photons on a Beam Splitter

Of course, any number of photons can be input into a beam splitter. For example, take the N-photon input state

The beam splitter acting on this state produces

The quantity on the right hand side can be re-expressed using the binomial theorem

where the permutations are defined by the binomial coefficient

The output state is given by

which is a “super” entangled state composed of N multi-photon states, involving N different universes.

Coherent States on a Quantum Beam Splitter

Surprisingly, there is a multi-photon input state that generates a non-entangled output—as if the input states were simply classical fields. These are the so-called coherent states, introduced by Glauber and Sudarshan [5, 6]. Coherent states can be described as superpositions of multi-photon states, but when a beam splitter operates on these superpositions, the outputs are simply 50/50 mixtures of the states. For instance, if the input scoherent tates are denoted by α and β, then the output states after the beam splitter are

This output is factorized and hence is NOT entangled. This is one of the many reasons why coherent states in quantum optics are considered the “most classical” of quantum states. In this case, a quantum beam splitter operates on the inputs just as if they were classical fields.

By David D. Nolte, May 8, 2022

References

[1] David D. Nolte, Interference: The History of Optical Interferometry and the Scientists who Tamed Light, (Oxford, July 2023)

[2] D. Deutsch, “Quantum-theory, the church-turing principle and the universal quantum computer,” Proceedings of the Royal Society of London Series a-Mathematical Physical and Engineering Sciences, vol. 400, no. 1818, pp. 97-117, (1985)

[3] D. Deutsch and R. Jozsa, “Rapid solution of problems by quantum computation,” Proceedings of the Royal Society of London Series a-Mathematical Physical and Engineering Sciences, vol. 439, no. 1907, pp. 553-558, Dec (1992)

[4] C. K. Hong, Z. Y. Ou, and L. Mandel, “Measurement of subpicosecond time intervals between 2 photons by interference,” Physical Review Letters, vol. 59, no. 18, pp. 2044-2046, Nov (1987)

[5] Glauber, R. J. (1963). “Photon Correlations.” Physical Review Letters 10(3): 84.

[6] Sudarshan, E. C. G. (1963). “Equivalence of semiclassical and quantum mechanical descriptions of statistical light beams.” Physical Review Letters 10(7): 277-&.; Mehta, C. L. and E. C. Sudarshan (1965). “Relation between quantum and semiclassical description of optical coherence.” Physical Review 138(1B): B274.

January 23, 2022August 16, 2025 by David D. Nolte

The Doppler Universe

If you are a fan of the Doppler effect, then time trials at the Indy 500 Speedway will floor you. Even if you have experienced the fall in pitch of a passing train whistle while stopped in your car at a railroad crossing, or heard the falling whine of a jet passing overhead, I can guarantee that you have never heard anything like an Indy car passing you by at 225 miles an hour.

Indy 500 Time Trials and the Doppler Effect

The Indy 500 time trials are the best way to experience the effect, rather than on race day when there is so much crowd noise and the overlapping sounds of all the cars. During the week before the race, the cars go out on the track, one by one, in time trials to decide the starting order in the pack on race day. Fans are allowed to wander around the entire complex, so you can get right up to the fence at track level on the straight-away. The cars go by only thirty feet away, so they are coming almost straight at you as they approach and straight away from you as they leave. The whine of the car as it approaches is 43% higher than when it is standing still, and it drops to 33% lower than the standing frequency—a ratio almost approaching a factor of two. And they go past so fast, it is almost a step function, going from a steady high note to a steady low note in less than a second. That is the Doppler effect!

But as obvious as the acoustic Doppler effect is to us today, it was far from obvious when it was proposed in 1842 by Christian Doppler at a time when trains, the fastest mode of transport at the time, ran at 20 miles per hour or less. In fact, Doppler’s theory generated so much controversy that the Academy of Sciences of Vienna held a trial in 1853 to decide its merit—and Doppler lost! For the surprising story of Doppler and the fate of his discovery, see my Physics Today article.

From that fraught beginning, the effect has expanded in such importance, that today it is a daily part of our lives. From Doppler weather radar, to speed traps on the highway, to ultrasound images of babies—Doppler is everywhere.

Development of the Doppler-Fizeau Effect

When Doppler proposed the shift in color of the light from stars in 1842 [1], depending on their motion towards or away from us, he may have been inspired by his walk to work every morning, watching the ripples on the surface of the Vltava River in Prague as the water slipped by the bridge piers. The drawings in his early papers look reminiscently like the patterns you see with compressed ripples on the upstream side of the pier and stretched out on the downstream side. Taking this principle to the night sky, Doppler envisioned that binary stars, where one companion was blue and the other was red, was caused by their relative motion. He could not have known at that time that typical binary star speeds were too small to cause this effect, but his principle was far more general, applying to all wave phenomena.

Six years later in 1848 [2], the French physicist Armand Hippolyte Fizeau, soon to be famous for making the first direct measurement of the speed of light, proposed the same principle, unaware of Doppler’s publications in German. As Fizeau was preparing his famous measurement, he originally worked with a spinning mirror (he would ultimately use a toothed wheel instead) and was thinking about what effect the moving mirror might have on the reflected light. He considered the effect of star motion on starlight, just as Doppler had, but realized that it was more likely that the speed of the star would affect the locations of the spectral lines rather than change the color. This is in fact the correct argument, because a Doppler shift on the black-body spectrum of a white or yellow star shifts a bit of the infrared into the visible red portion, while shifting a bit of the ultraviolet out of the visible, so that the overall color of the star remains the same, but Fraunhofer lines would shift in the process. Because of the independent development of the phenomenon by both Doppler and Fizeau, and because Fizeau was a bit clearer in the consequences, the effect is more accurately called the Doppler-Fizeau Effect, and in France sometimes only as the Fizeau Effect. Here in the US, we tend to forget the contributions of Fizeau, and it is all Doppler.

Fig. 1 The title page of Doppler’s 1842 paper [1] proposing the shift in color of stars caused by their motions. (“On the colored light of double stars and a few other stars in the heavens: Study of an integral part of Bradley’s general aberration theory”)

Fig. 2 Doppler used simple proportionality and relative velocities to deduce the first-order change in frequency of waves caused by motion of the source relative to the receiver, or of the receiver relative to the source.

Fig. 3 Doppler’s drawing of what would later be called the Mach cone generating a shock wave. Mach was one of Doppler’s later champions, making dramatic laboratory demonstrations of the acoustic effect, even as skepticism persisted in accepting the phenomenon.

Doppler and Exoplanet Discovery

It is fitting that many of today’s applications of the Doppler effect are in astronomy. His original idea on binary star colors was wrong, but his idea that relative motion changes frequencies was right, and it has become one of the most powerful astrometric techniques in astronomy today. One of its important recent applications was in the discovery of extrasolar planets orbiting distant stars.

When a large planet like Jupiter orbits a star, the center of mass of the two-body system remains at a constant point, but the individual centers of mass of the planet and the star both orbit the common point. This makes it look like the star has a wobble, first moving towards our viewpoint on Earth, then moving away. Because of this relative motion of the star, the light can appear blueshifted caused by the Doppler effect, then redshifted with a set periodicity. This was observed by Queloz and Mayer in 1995 for the star 51 Pegasi, which represented the first detection of an exoplanet [3]. The duo won the Nobel Prize in 2019 for the discovery.

Fig. 4 A gas giant (like Jupiter) and a star obit a common center of mass causing the star to wobble. The light of the star when viewed at Earth is periodically red- and blue-shifted by the Doppler effect. From Ref.

Doppler and Vera Rubins’ Galaxy Velocity Curves

In the late 1960’s and early 1970’s Vera Rubin at the Carnegie Institution of Washington used newly developed spectrographs to use the Doppler effect to study the speeds of ionized hydrogen gas surrounding massive stars in individual galaxies [4]. From simple Newtonian dynamics it is well understood that the speed of stars as a function of distance from the galactic center should increase with increasing distance up to the average radius of the galaxy, and then should decrease at larger distances. This trend in speed as a function of radius is called a rotation curve. As Rubin constructed the rotation curves for many galaxies, the increase of speed with increasing radius at small radii emerged as a clear trend, but the stars farther out in the galaxies were all moving far too fast. In fact, they are moving so fast that they exceeded escape velocity and should have flown off into space long ago. This disturbing pattern was repeated consistently in one rotation curve after another for many galaxies.

Fig. 5 Locations of Doppler shifts of ionized hydrogen measured by Vera Rubin on the Andromeda galaxy. From Ref.

Fig. 6 Vera Rubin’s velocity curve for the Andromeda galaxy. From Ref.

Fig. 7 Measured velocity curves relative to what is expected from the visible mass distribution of the galaxy. From Ref.

A simple fix to the problem of the rotation curves is to assume that there is significant mass present in every galaxy that is not observable either as luminous matter or as interstellar dust. In other words, there is unobserved matter, dark matter, in all galaxies that keeps all their stars gravitationally bound. Estimates of the amount of dark matter needed to fix the velocity curves is about five times as much dark matter as observable matter. In short, 80% of the mass of a galaxy is not normal. It is neither a perturbation nor an artifact, but something fundamental and large. The discovery of the rotation curve anomaly by Rubin using the Doppler effect stands as one of the strongest evidence for the existence of dark matter.

There is so much dark matter in the Universe that it must have a major effect on the overall curvature of space-time according to Einstein’s field equations. One of the best probes of the large-scale structure of the Universe is the afterglow of the Big Bang, known as the cosmic microwave background (CMB).

Doppler and the Big Bang

The Big Bang was astronomically hot, but as the Universe expanded it cooled. About 380,000 years after the Big Bang, the Universe cooled sufficiently that the electron-proton plasma that filled space at that time condensed into hydrogen. Plasma is charged and opaque to photons, while hydrogen is neutral and transparent. Therefore, when the hydrogen condensed, the thermal photons suddenly flew free and have continued unimpeded, continuing to cool. Today the thermal glow has reached about three degrees above absolute zero. Photons in thermal equilibrium with this low temperature have an average wavelength of a few millimeters corresponding to microwave frequencies, which is why the afterglow of the Big Bang got its name: the Cosmic Microwave Background (CMB).

Not surprisingly, the CMB has no preferred reference frame, because every point in space is expanding relative to every other point in space. In other words, space itself is expanding. Yet soon after the CMB was discovered by Arno Penzias and Robert Wilson (for which they were awarded the Nobel Prize in Physics in 1978), an anisotropy was discovered in the background that had a dipole symmetry caused by the Doppler effect as the Solar System moves at 368±2 km/sec relative to the rest frame of the CMB. Our direction is towards galactic longitude 263.85^o and latitude 48.25^o, or a bit southwest of Virgo. Interestingly, the local group of about 100 galaxies, of which the Milky Way and Andromeda are the largest members, is moving at 627±22 km/sec in the direction of galactic longitude 276^o and latitude 30^o. Therefore, it seems like we are a bit slack in our speed compared to the rest of the local group. This is in part because we are being pulled towards Andromeda in roughly the opposite direction, but also because of the speed of the solar system in our Galaxy.

Fig. 8 The CMB dipole anisotropy caused by the Doppler effect as the Earth moves at 368 km/sec through the rest frame of the CMB.

Aside from the dipole anisotropy, the CMB is amazingly uniform when viewed from any direction in space, but not perfectly uniform. At the level of 0.005 percent, there are variations in the temperature depending on the location on the sky. These fluctuations in background temperature are called the CMB anisotropy, and they help interpret current models of the Universe. For instance, the average angular size of the fluctuations is related to the overall curvature of the Universe. This is because, in the early Universe, not all parts of it were in communication with each other. This set an original spatial size to thermal discrepancies. As the Universe continued to expand, the size of the regional variations expanded with it, and the sizes observed today would appear larger or smaller, depending on how the universe is curved. Therefore, to measure the energy density of the Universe, and hence to find its curvature, required measurements of the CMB temperature that were accurate to better than a part in 10,000.

Equivalently, parts of the early universe had greater mass density than others, causing the gravitational infall of matter towards these regions. Then, through the Doppler effect, light emitted (or scattered) by matter moving towards these regions contributes to the anisotropy. They contribute what are known as “Doppler peaks” in the spatial frequency spectrum of the CMB anisotropy.

Fig. 9 The CMB small-scale anisotropy, part of which is contributed by Doppler shifts of matter falling into denser regions in the early universe.

The examples discussed in this blog (exoplanet discovery, galaxy rotation curves, and cosmic background) are just a small sampling of the many ways that the Doppler effect is used in Astronomy. But clearly, Doppler has played a key role in the long history of the universe.

By David D. Nolte, Jan. 23, 2022

References:

[1] C. A. DOPPLER, “Über das farbige Licht der Doppelsterne und einiger anderer Gestirne des Himmels (About the coloured light of the binary stars and some other stars of the heavens),” Proceedings of the Royal Bohemian Society of Sciences, vol. V, no. 2, pp. 465–482, (Reissued 1903) (1842)

[2] H. Fizeau, “Acoustique et optique,” presented at the Société Philomathique de Paris, Paris, 1848.

[3] M. Mayor and D. Queloz, “A JUPITER-MASS COMPANION TO A SOLAR-TYPE STAR,” Nature, vol. 378, no. 6555, pp. 355-359, Nov (1995)

[4] Rubin, Vera; Ford, Jr., W. Kent (1970). “Rotation of the Andromeda Nebula from a Spectroscopic Survey of Emission Regions”. The Astrophysical Journal. 159: 379

Twenty Years at Light Speed: The Future of Photonic Quantum Computing

Now is exactly the wrong moment to be reviewing the state of photonic quantum computing — the field is moving so rapidly, at just this moment, that everything I say here now will probably be out of date in just a few years. On the other hand, now is exactly the right time to be doing this review, because so much has happened in just the past few years, that it is important to take a moment and look at where this field is today and where it will be going.

At the 20-year anniversary of the publication of my book Mind at Light Speed (Free Press, 2001), this blog is the third in a series reviewing progress in three generations of Machines of Light over the past 20 years (see my previous blogs on the future of the photonic internet and on all-optical computers). This third and final update reviews progress on the third generation of the Machines of Light: the Quantum Optical Generation. Of the three generations, this is the one that is changing the fastest.

Quantum computing is almost here … and it will be at room temperature, using light, in photonic integrated circuits!

Quantum Computing with Linear Optics

Twenty years ago in 2001, Emanuel Knill and Raymond LaFlamme at Los Alamos National Lab, with Gerald Mulburn at the University of Queensland, Australia, published a revolutionary theoretical paper (known as KLM) in Nature on quantum computing with linear optics: “A scheme for efficient quantum computation with linear optics” [1]. Up until that time, it was believed that a quantum computer — if it was going to have the property of a universal Turing machine — needed to have at least some nonlinear interactions among qubits in a quantum gate. For instance, an example of a two-qubit gate is a controlled-NOT, or CNOT, gate shown in Fig. 1 with the Truth Table and the equivalent unitary matrix. It clear that one qubit is controlling the other, telling it what to do.

The quantum CNOT gate gets interesting when the control line has a quantum superposition, then the two outputs become entangled.

Entanglement is a strange process that is unique to quantum systems and has no classical analog. It also has no simple intuitive explanation. By any normal logic, if the control line passes through the gate unaltered, then absolutely nothing interesting should be happening on the Control-Out line. But that’s not the case. The control line going in was a separate state. If some measurement were made on it, either a 1 or 0 would be seen with equal probability. But coming out of the CNOT, the signal has somehow become perfectly correlated with whatever value is on the Signal-Out line. If the Signal-Out is measured, the measurement process collapses the state of the Control-Out to a value equal to the measured signal. The outcome of the control line becomes 100% certain even though nothing was ever done to it! This entanglement generation is one reason the CNOT is often the gate of choice when constructing quantum circuits to perform interesting quantum algorithms.

However, optical implementation of a CNOT is a problem, because light beams and photons really do not like to interact with each other. This is the problem with all-optical classical computers too (see my previous blog). There are ways of getting light to interact with light, for instance inside nonlinear optical materials. And in the case of quantum optics, a single atom in an optical cavity can interact with single photons in ways that can act like a CNOT or related gates. But the efficiencies are very low and the costs to implement it are very high, making it difficult or impossible to scale such systems up into whole networks needed to make a universal quantum computer.

Therefore, when KLM published their idea for quantum computing with linear optics, it caused a shift in the way people were thinking about optical quantum computing. A universal optical quantum computer could be built using just light sources, beam splitters and photon detectors.

The way that KLM gets around the need for a direct nonlinear interaction between two photons is to use postselection. They run a set of photons — signal photons and ancilla (test) photons — through their linear optical system and they detect (i.e., theoretically…the paper is purely a theoretical proposal) the ancilla photons. If these photons are not detected where they are wanted, then that iteration of the computation is thrown out, and it is tried again and again, until the photons end up where they need to be. When the ancilla outcomes are finally what they need to be, this run is selected because the signal state are known to have undergone a known transformation. The signal photons are still unmeasured at this point and are therefore in quantum superpositions that are useful for quantum computation. Postselection uses entanglement and measurement collapse to put the signal photons into desired quantum states. Postselection provides an effective nonlinearity that is induced by the wavefunction collapse of the entangled state. Of course, the down side of this approach is that many iterations are thrown out — the computation becomes non-deterministic.

KLM could get around most of the non-determinism by using more and more ancilla photons, but this has the cost of blowing up the size and cost of the implementation, so their scheme was not imminently practical. But the important point was that it introduced the idea of linear quantum computing. (For this, Milburn and his collaborators have my vote for a future Nobel Prize.) Once that idea was out, others refined it, and improved upon it, and found clever ways to make it more efficient and more scalable. Many of these ideas relied on a technology that was co-evolving with quantum computing — photonic integrated circuits (PICs).

Quantum Photonic Integrated Circuits (QPICs)

Never underestimate the power of silicon. The amount of time and energy and resources that have now been invested in silicon device fabrication is so astronomical that almost nothing in this world can displace it as the dominant technology of the present day and the future. Therefore, when a photon can do something better than an electron, you can guess that eventually that photon will be encased in a silicon chip–on a photonic integrated circuit (PIC).

The dream of integrated optics (the optical analog of integrated electronics) has been around for decades, where waveguides take the place of conducting wires, and interferometers take the place of transistors — all miniaturized and fabricated in the thousands on silicon wafers. The advantages of PICs are obvious, but it has taken a long time to develop. When I was a post-doc at Bell Labs in the late 1980’s, everyone was talking about PICs, but they had terrible fabrication challenges and terrible attenuation losses. Fortunately, these are just technical problems, not limited by any fundamental laws of physics, so time (and an army of researchers) has chipped away at them.

One of the driving forces behind the maturation of PIC technology is photonic fiber optic communications (as discussed in a previous blog). Photons are clear winners when it comes to long-distance communications. In that sense, photonic information technology is a close cousin to silicon — photons are no less likely to be replaced by a future technology than silicon is. Therefore, it made sense to bring the photons onto the silicon chips, tapping into the full array of silicon fab resources so that there could be seamless integration between fiber optics doing the communications and the photonic chips directing the information. Admittedly, photonic chips are not yet all-optical. They still use electronics to control the optical devices on the chip, but this niche for photonics has provided a driving force for advancements in PIC fabrication.

Fig. 2 Schematic of a silicon photonic integrated circuit (PIC). The waveguides can be silica or nitride deposited on the silicon chip. From the Comsol WebSite.

One side-effect of improved PIC fabrication is low light losses. In telecommunications, this loss is not so critical because the systems use OEO regeneration. But less loss is always good, and the PICs can now safeguard almost every photon that comes on chip — exactly what is needed for a quantum PIC. In a quantum photonic circuit, every photon is valuable and informative and needs to be protected. The new PIC fabrication can do this. In addition, light switches for telecom applications are built from integrated interferometers on the chip. It turns out that interferometers at the single-photon level are unitary quantum gates that can be used to build universal photonic quantum computers. So the same technology and control that was used for telecom is just what is needed for photonic quantum computers. In addition, integrated optical cavities on the PICs, which look just like wavelength filters when used for classical optics, are perfect for producing quantum states of light known as squeezed light that turn out to be valuable for certain specialty types of quantum computing.

Therefore, as the concepts of linear optical quantum computing advanced through that last 20 years, the hardware to implement those concepts also advanced, driven by a highly lucrative market segment that provided the resources to tap into the vast miniaturization capabilities of silicon chip fabrication. Very fortuitous!

Room-Temperature Quantum Computers

There are many radically different ways to make a quantum computer. Some are built of superconducting circuits, others are made from semiconductors, or arrays of trapped ions, or nuclear spins on nuclei on atoms in molecules, and of course with photons. Up until about 5 years ago, optical quantum computers seemed like long shots. Perhaps the most advanced technology was the superconducting approach. Superconducting quantum interference devices (SQUIDS) have exquisite sensitivity that makes them robust quantum information devices. But the drawback is the cold temperatures that are needed for them to work. Many of the other approaches likewise need cold temperature–sometimes astronomically cold temperatures that are only a few thousandths of a degree above absolute zero Kelvin.

Cold temperatures and quantum computing seemed a foregone conclusion — you weren’t ever going to separate them — and for good reason. The single greatest threat to quantum information is decoherence — the draining away of the kind of quantum coherence that allows interferences and quantum algorithms to work. In this way, entanglement is a two-edged sword. On the one hand, entanglement provides one of the essential resources for the exponential speed-up of quantum algorithms. But on the other hand, if a qubit “sees” any environmental disturbance, then it becomes entangled with that environment. The entangling of quantum information with the environment causes the coherence to drain away — hence decoherence. Hot environments disturb quantum systems much more than cold environments, so there is a premium for cooling the environment of quantum computers to as low a temperature as they can. Even so, decoherence times can be microseconds to milliseconds under even the best conditions — quantum information dissipates almost as fast as you can make it.

Enter the photon! The bottom line is that photons don’t interact. They are blind to their environment. This is what makes them perfect information carriers down fiber optics. It is also what makes them such good qubits for carrying quantum information. You can prepare a photon in a quantum superposition just by sending it through a lossless polarizing crystal, and then the superposition will last for as long as you can let the photon travel (at the speed of light). Sometimes this means putting the photon into a coil of fiber many kilometers long to store it, but that is OK — a kilometer of coiled fiber in the lab is no bigger than a few tens of centimeters. So the same properties that make photons excellent at carrying information also gives them very small decoherence. And after the KLM schemes began to be developed, the non-interacting properties of photons were no longer a handicap.

In the past 5 years there has been an explosion, as well as an implosion, of quantum photonic computing advances. The implosion is the level of integration which puts more and more optical elements into smaller and smaller footprints on silicon PICs. The explosion is the number of first-of-a-kind demonstrations: the first universal optical quantum computer [2], the first programmable photonic quantum computer [3], and the first (true) quantum computational advantage [4].

All of these “firsts” operate at room temperature. (There is a slight caveat: The photon-number detectors are actually superconducting wire detectors that do need to be cooled. But these can be housed off-chip and off-rack in a separate cooled system that is coupled to the quantum computer by — no surprise — fiber optics.) These are the advantages of photonic quantum computers: hundreds of qubits integrated onto chips, room-temperature operation, long decoherence times, compatibility with telecom light sources and PICs, compatibility with silicon chip fabrication, universal gates using postselection, and more. Despite the head start of some of the other quantum computing systems, photonics looks like it will be overtaking the others within only a few years to become the dominant technology for the future of quantum computing. And part of that future is being helped along by a new kind of quantum algorithm that is perfectly suited to optics.

Fig. 3 Superconducting photon counting detector. From WebSite

A New Kind of Quantum Algorithm: Boson Sampling

In 2011, Scott Aaronson (then at at MIT) published a landmark paper titled “The Computational Complexity of Linear Optics” with his post-doc, Anton Arkhipov [5]. The authors speculated on whether there could be an application of linear optics, not requiring the costly step of post-selection, that was still useful for applications, while simultaneously demonstrating quantum computational advantage. In other words, could one find a linear optical system working with photons that could solve problems intractable to a classical computer? To their own amazement, they did! The answer was something they called “boson sampling”.

To get an idea of what boson sampling is, and why it is very hard to do on a classical computer, think of the classic demonstration of the normal probability distribution found at almost every science museum you visit, illustrated in Fig. 2. A large number of ping-pong balls are dropped one at a time through a forest of regularly-spaced posts, bouncing randomly this way and that until they are collected into bins at the bottom. Bins near the center collect many balls, while bins farther to the side have fewer. If there are many balls, then the stacked heights of the balls in the bins map out a Gaussian probability distribution. The path of a single ping-pong ball represents a series of “decisions” as it hits each post and goes left or right, and the number of permutations of all the possible decisions among all the other ping-pong balls grows exponentially—a hard problem to tackle on a classical computer.

Fig. 4 Ping-pont ball normal distribution. Watch the YouTube video.

In the paper, Aaronson considered a quantum analog to the ping-pong problem in which the ping-pong balls are replaced by photons, and the posts are replaced by beam splitters. As its simplest possible implementation, it could have two photon channels incident on a single beam splitter. The well-known result in this case is the “HOM dip” [6] which is a consequence of the boson statistics of the photon. Now scale this system up to many channels and a cascade of beam splitters, and one has an N-channel multi-photon HOM cascade. The output of this photonic “circuit” is a sampling of the vast number of permutations allowed by bose statistics—boson sampling.

To make the problem more interesting, Aaronson allowed the photons to be launched from any channel at the top (as opposed to dropping all the ping-pong balls at the same spot), and they allowed each beam splitter to have adjustable phases (photons and phases are the key elements of an interferometer). By adjusting the locations of the photon channels and the phases of the beam splitters, it would be possible to “program” this boson cascade to mimic interesting quantum systems or even to solve specific problems, although they were not thinking that far ahead. The main point of the paper was the proposal that implementing boson sampling in a photonic circuit used resources that scaled linearly in the number of photon channels, while the problems that could be solved grew exponentially—a clear quantum computational advantage [4].

On the other hand, it turned out that boson sampling is not universal—one cannot construct a universal quantum computer out of boson sampling. The first proposal was a specialty algorithm whose main function was to demonstrate quantum computational advantage rather than do something specifically useful—just like Deutsch’s first algorithm. But just like Deutsch’s algorithm, which led ultimately to Shor’s very useful prime factoring algorithm, boson sampling turned out to be the start of a new wave of quantum applications.

Shortly after the publication of Aaronson’s and Arkhipov’s paper in 2011, there was a flurry of experimental papers demonstrating boson sampling in the laboratory [7, 8]. And it was discovered that boson sampling could solve important and useful problems, such as the energy levels of quantum systems, and network similarity, as well as quantum random-walk problems. Therefore, even though boson sampling is not strictly universal, it solves a broad class of problems. It can be viewed more like a specialty chip than a universal computer, like the now-ubiquitous GPU’s are specialty chips in virtually every desktop and laptop computer today. And the room-temperature operation significantly reduces cost, so you don’t need a whole government agency to afford one. Just like CPU costs followed Moore’s Law to the point where a Raspberry Pi computer costs $40 today, the photonic chips may get onto their own Moore’s Law that will reduce costs over the next several decades until they are common (but still specialty and probably not cheap) computers in academia and industry. A first step along that path was a recently-demonstrated general programmable room-temperature photonic quantum computer.

Fig. 5 A classical Galton board on the left, and a photon-based boson sampling on the right. From the Walmsley (Oxford) WebSite.

A Programmable Photonic Quantum Computer: Xanadu’s X8 Chip

I don’t usually talk about specific companies, but the new photonic quantum computer chip from Xanadu, based in Toronto, Canada, feels to me like the start of something big. In the March 4, 2021 issue of Nature magazine, researchers at the company published the experimental results of their X8 photonic chip [3]. The chip uses boson sampling of strongly non-classical light. This was the first generally programmable photonic quantum computing chip, programmed using a quantum programming language they developed called Strawberry Fields. By simply changing the quantum code (using a simple conventional computer interface), they switched the computer output among three different quantum applications: transitions among states (spectra of molecular states), quantum docking, and similarity between graphs that represent two different molecules. These are radically different physics and math problems, yet the single chip can be programmed on the fly to solve each one.

The chip is constructed of nitride waveguides on silicon, shown in Fig. 6. The input lasers drive ring oscillators that produce squeezed states through four-wave mixing. The key to the reprogrammability of the chip is the set of phase modulators that use simple thermal changes on the waveguides. These phase modulators are changed in response to commands from the software to reconfigure the application. Although they switch slowly, once they are set to their new configuration, the computations take place “at the speed of light”. The photonic chip is at room temperature, but the outputs of the four channels are sent by fiber optic to a cooled unit containing the superconductor nanowire photon counters.

Fig. 6 The Xanadu X8 photonic quantum computing chip. From Ref.

Fig. 7 To see the chip in operation, see the YouTube video.

Admittedly, the four channels of the X8 chip are not large enough to solve the kinds of problems that would require a quantum computer, but the company has plans to scale the chip up to 100 channels. One of the challenges is to reduce the amount of photon loss in a multiplexed chip, but standard silicon fabrication approaches are expected to reduce loss in the next generation chips by an order of magnitude.

Additional companies are also in the process of entering the photonic quantum computing business, such as PsiQuantum, which recently closed a $450M funding round to produce photonic quantum chips with a million qubits. The company is led by Jeremy O’Brien from Bristol University who has been a leader in photonic quantum computing for over a decade.

Stay tuned!

By David D. Nolte, Dec. 20, 2021

References

[1] E. Knill, R. Laflamme, and G. J. Milburn, “A scheme for efficient quantum computation with linear optics,” Nature, vol. 409, no. 6816, pp. 46-52, Jan (2001)

KLM01 Download

[2] J. Carolan, J. L. O’Brien et al, “Universal linear optics,” Science, vol. 349, no. 6249, pp. 711-716, Aug (2015)

[3] J. M. Arrazola, et al, “Quantum circuits with many photons on a programmable nanophotonic chip,” Nature, vol. 591, no. 7848, pp. 54-+, Mar (2021)

[4] H.-S. Zhong J.-W. Pan et al, “Quantum computational advantage using photons,” Science, vol. 370, no. 6523, p. 1460, (2020)

[5] S. Aaronson and A. Arkhipov, “The Computational Complexity of Linear Optics,” in 43rd ACM Symposium on Theory of Computing, San Jose, CA, Jun 06-08 2011, NEW YORK: Assoc Computing Machinery, in Annual ACM Symposium on Theory of Computing, 2011, pp. 333-342

[6] C. K. Hong, Z. Y. Ou, and L. Mandel, “Measurement of subpicosecond time intervals between 2 photons by interference,” Physical Review Letters, vol. 59, no. 18, pp. 2044-2046, Nov (1987)

[7] J. B. Spring, I. A. Walmsley et al, “Boson Sampling on a Photonic Chip,” Science, vol. 339, no. 6121, pp. 798-801, Feb (2013)

[8] M. A. Broome, A. Fedrizzi, S. Rahimi-Keshari, J. Dove, S. Aaronson, T. C. Ralph, and A. G. White, “Photonic Boson Sampling in a Tunable Circuit,” Science, vol. 339, no. 6121, pp. 794-798, Feb (2013)

Interference (New from Oxford University Press, 2023)

Read the stories of the scientists and engineers who tamed light and used it to probe the universe.

Available from Amazon.

Available from Oxford U Press

Available from Barnes & Nobles

Anant K. Ramdas

Semiconductor Physics at Purdue

The Golden Age of Physics

Selected Topics of Research from Anant Ramdas

Diamond

Magneto-Optics

Shallow Defects in Semiconductors

Dynamic Defects in Semiconductors

Beyond the Golden Age?

References

Other Notable Papers:

Early Days

Purdue University and Prof. Lark-Horowitz

Radiation Laboratory, MIT

Nuclear Magnetic Resonance

References and Notes

1. Thomas Young Polymath: The Law of Interference

2. The Fresnel Connection: Particles versus Waves

3. At Light Speed

4. After the Gold Rush

5. Stellar Interference

6. Across the Universe

7. Two Faces of Microscopy

8. Holographic Dreams of Princess Leia

9. Photon Interference

10. The Quantum Advantage

References:

Further Reading: The History of Light and Interference (2023)

Augustin Fresnel: Ironic Rebel of Physics

Stellar Aberration and the Fresnel Drag Coefficient

Fizeau’s Moving Water Experiment

Einstein’s Insight

Further Reading

Jean Picard at Uranibourg

Samuel Molyneux and Murder in Kew

James Bradley and the Light Wind

Chapter 1. Thomas Young Polymath: The Law of Interference

Chapter 2. The Fresnel Connection: Particles versus Waves

Chapter 3. At Light Speed: The Birth of Interferometry

Chapter 4. After the Gold Rush: The Trials of Albert Michelson

Chapter 5. Stellar Interference: Measuring the Stars

And More

New from Oxford Press: The History of Light and Interference (2023)

Resurrecting MWI in the Name of Quantum Information

The Classical Beam Splitter

The Quantum Beam Splitter

The Hong-Ou-Mandel (HOM) Interferometer

N-Photons on a Beam Splitter

Coherent States on a Quantum Beam Splitter

Read more in “Interference” (New from Oxford University Press, 2023)

References

Indy 500 Time Trials and the Doppler Effect

Development of the Doppler-Fizeau Effect

Doppler and Exoplanet Discovery

Doppler and Vera Rubins’ Galaxy Velocity Curves

Doppler and the Big Bang

References:

Further Reading

Quantum Computing with Linear Optics

Quantum Photonic Integrated Circuits (QPICs)

Room-Temperature Quantum Computers

A New Kind of Quantum Algorithm: Boson Sampling

A Programmable Photonic Quantum Computer: Xanadu’s X8 Chip

Further Reading

References

Interference (New from Oxford University Press, 2023)