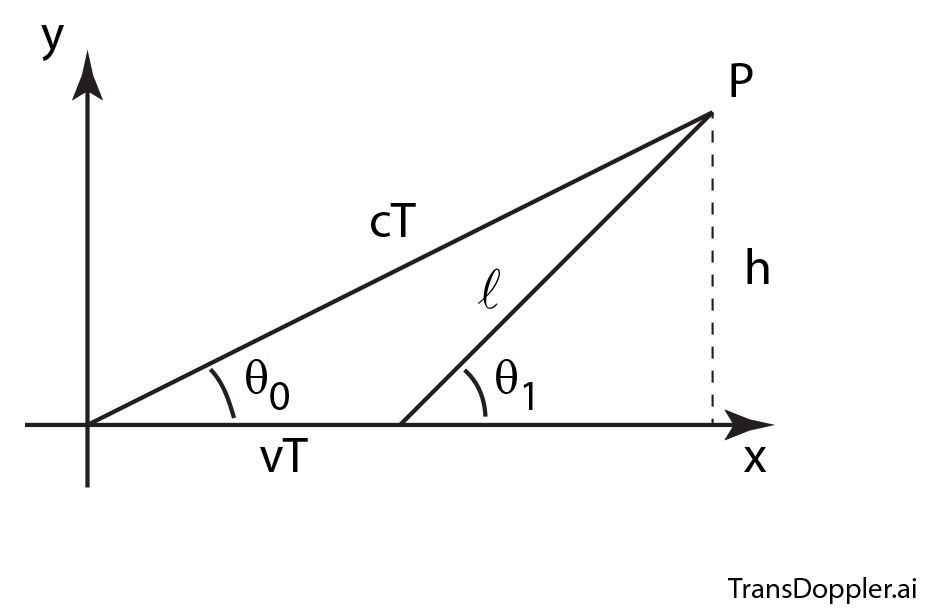
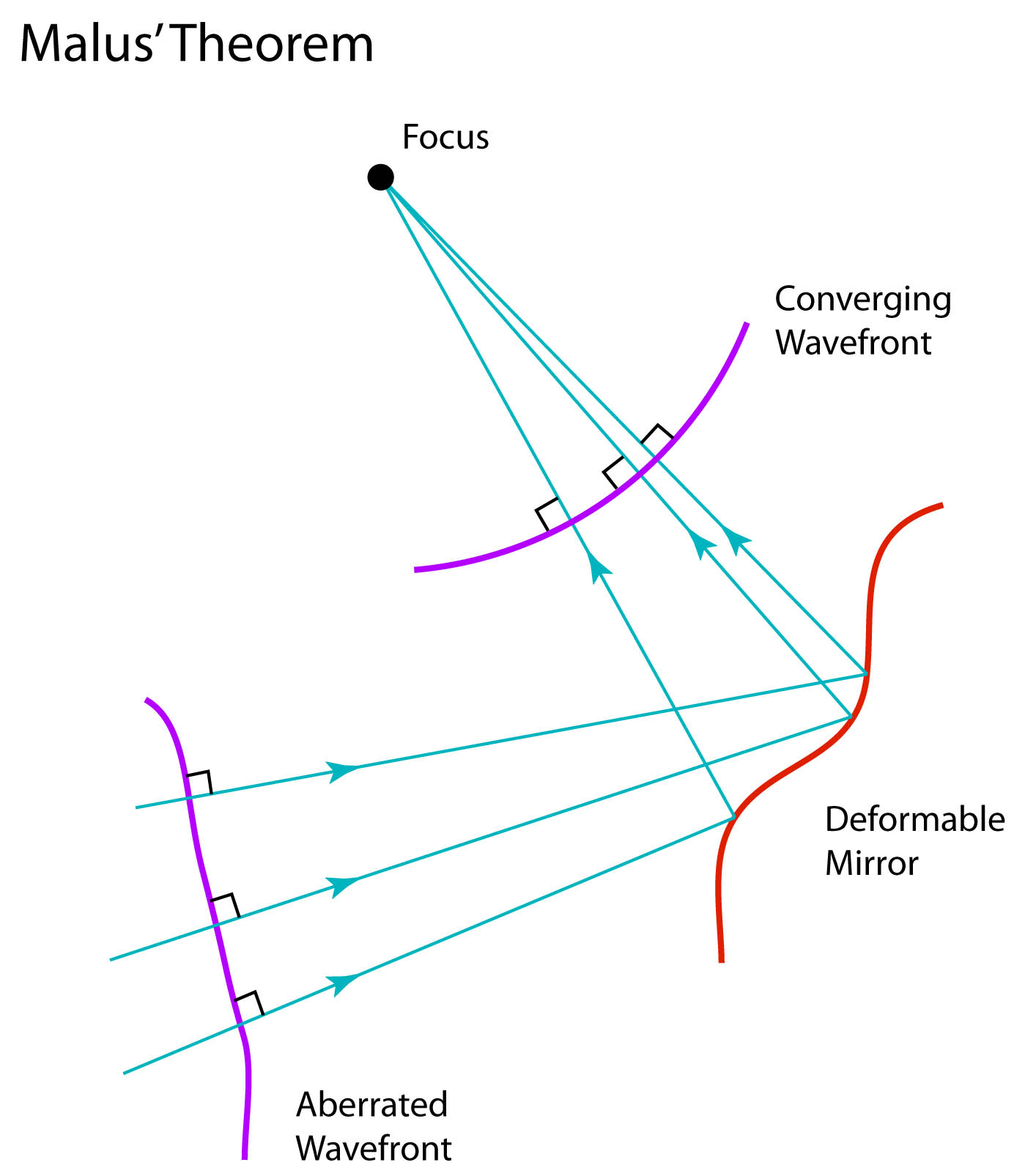
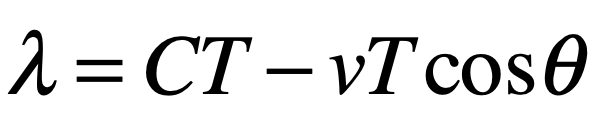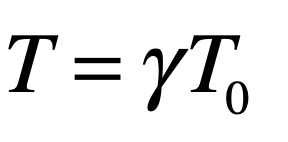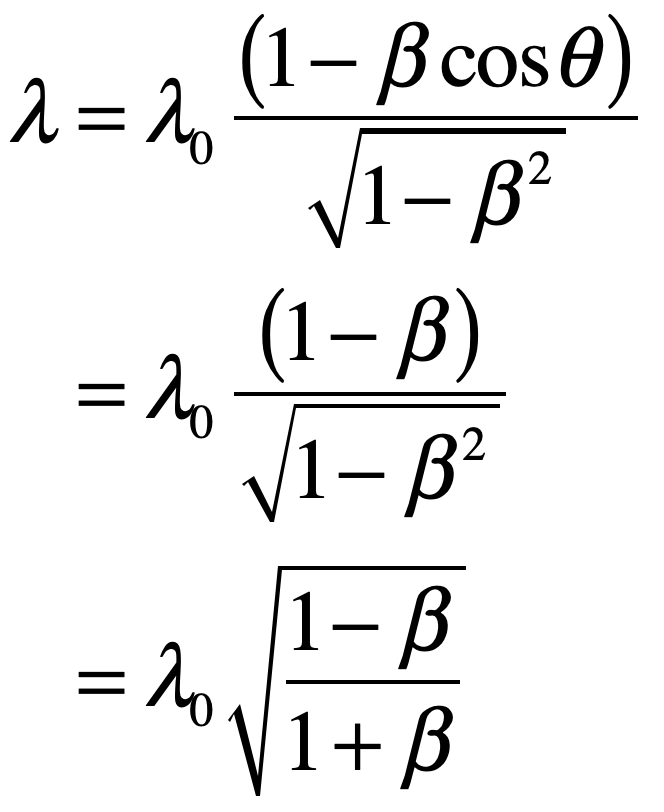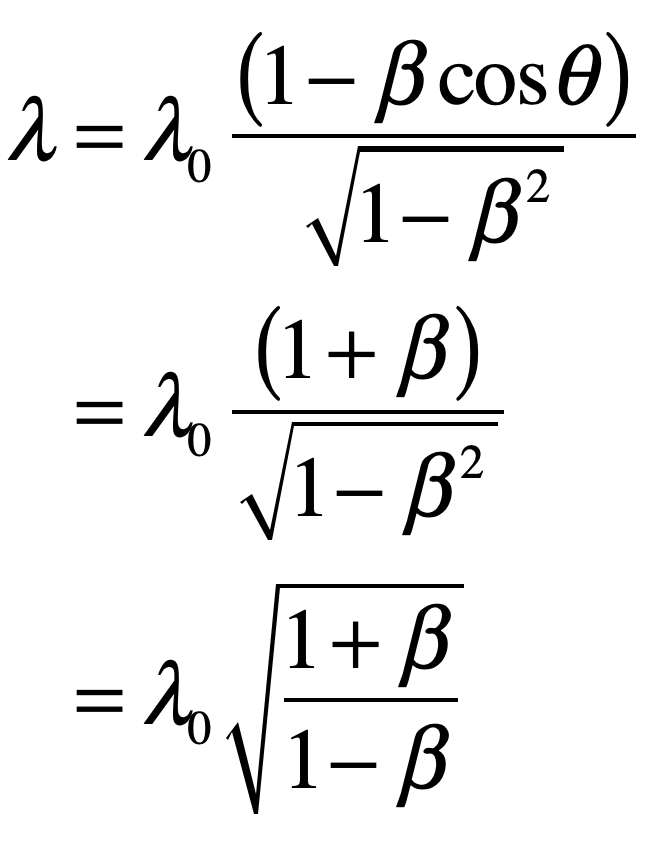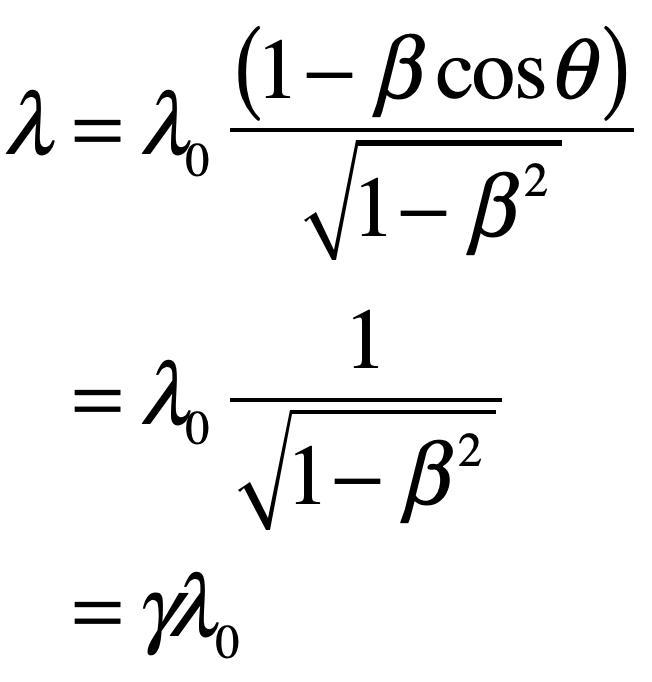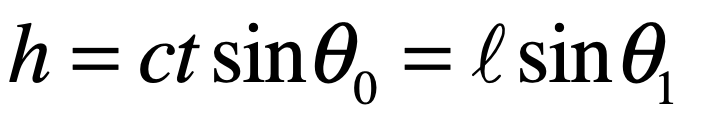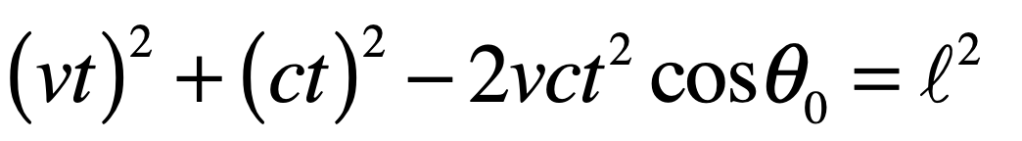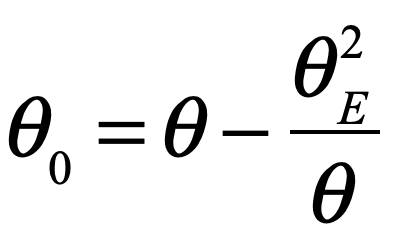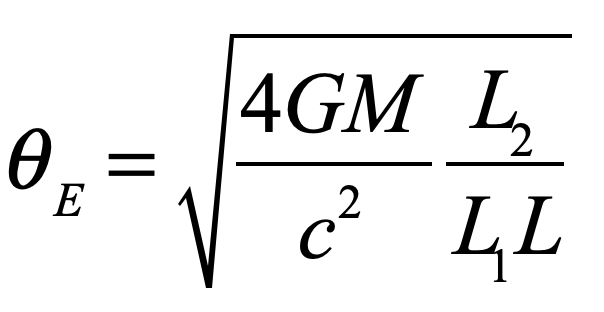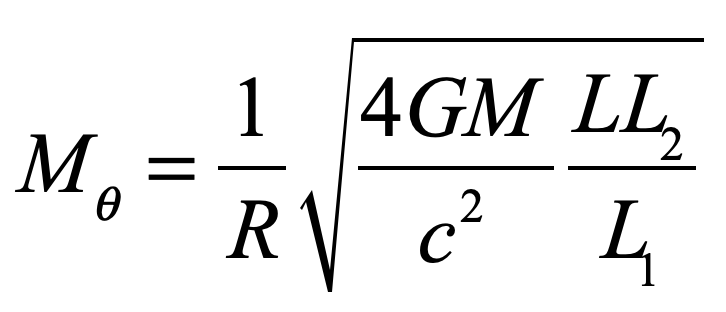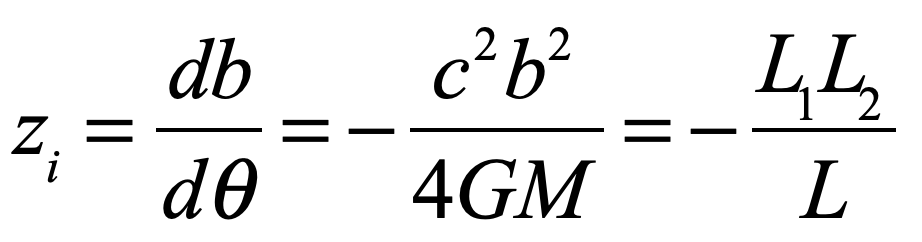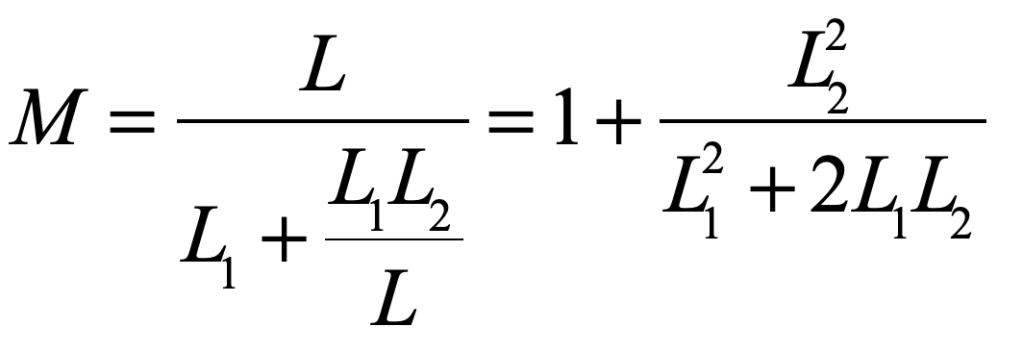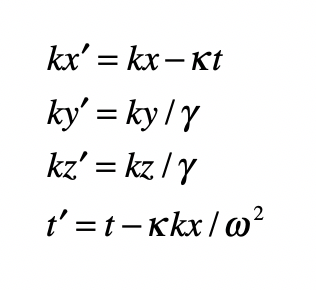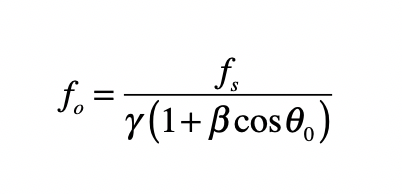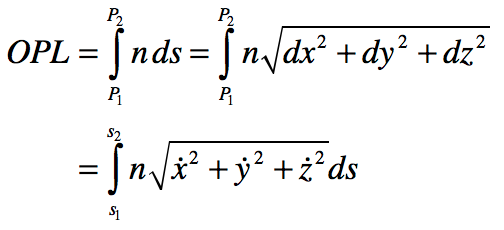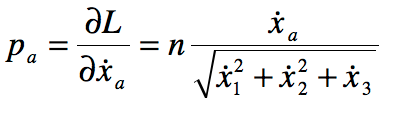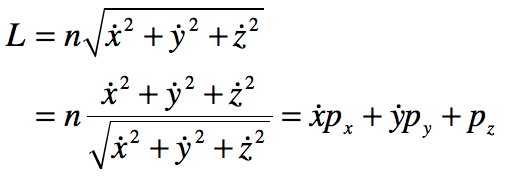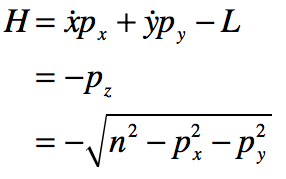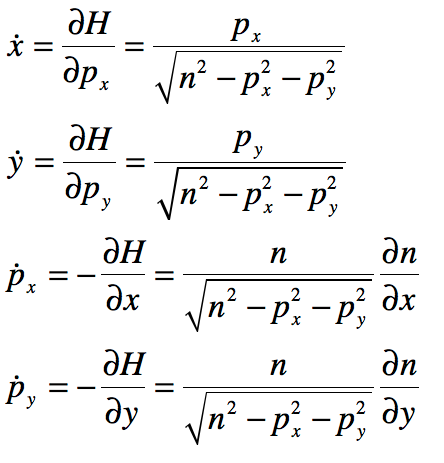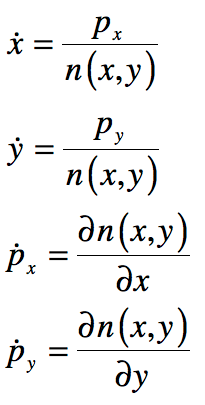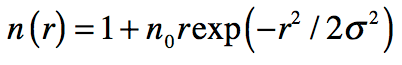November 28, 2021February 9, 2023 by David D. Nolte

Twenty Years at Light Speed: Photonic Computing

In the epilog of my book Mind at Light Speed: A New Kind of Intelligence (Free Press, 2001), I speculated about a future computer in which sheets of light interact with others to form new meanings and logical cascades as light makes decisions in a form of all-optical intelligence.

Twenty years later, that optical computer seems vaguely quaint, not because new technology has passed it by, like looking at the naïve musings of Jules Verne from our modern vantage point, but because the optical computer seems almost as far away now as it did back in 2001.

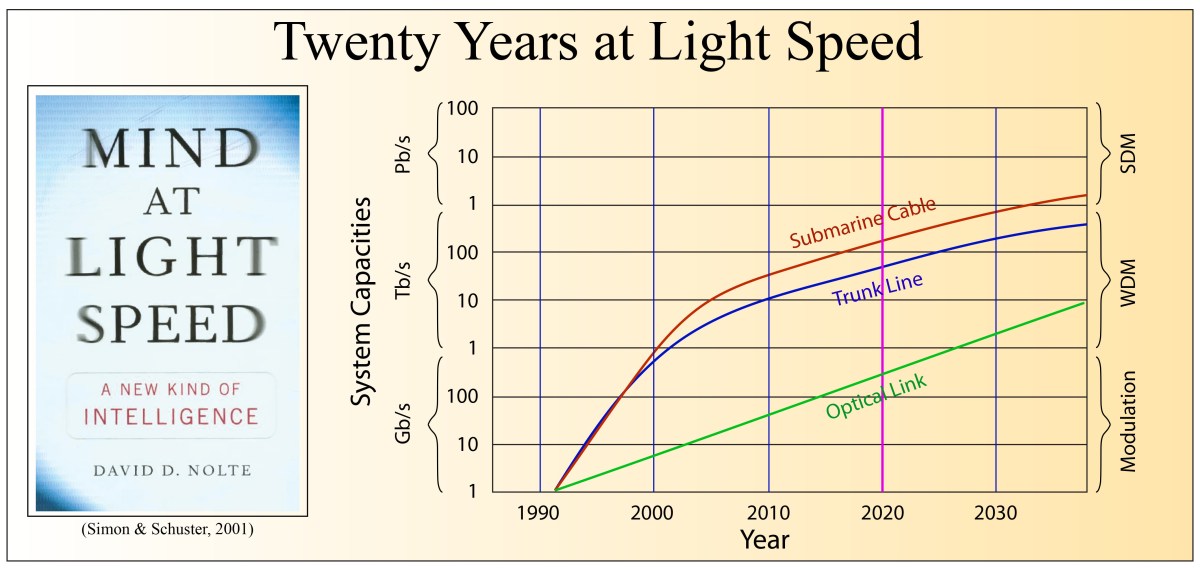
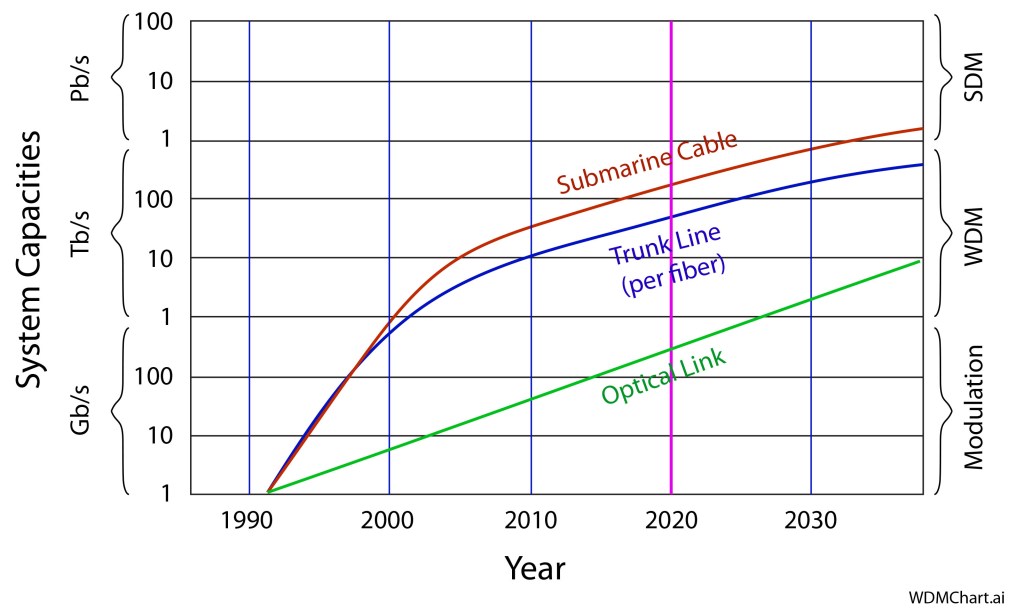
At the the turn of the Millennium we were seeing tremendous advances in data rates on fiber optics (see my previous Blog) as well as the development of new types of nonlinear optical devices and switches that served the role of rudimentary logic switches. At that time, it was not unreasonable to believe that the pace of progress would remain undiminished, and that by 2020 we would have all-optical computers and signal processors in which the same optical data on the communication fibers would be involved in the logic that told the data what to do and where to go—all without the wasteful and slow conversion to electronics and back again into photons—the infamous OEO conversion.

However, the rate of increase of the transmission bandwidth on fiber optic cables slowed not long after the publication of my book, and nonlinear optics today still needs high intensities to be efficient, which remains a challenge for significant (commercial) use of all-optical logic.

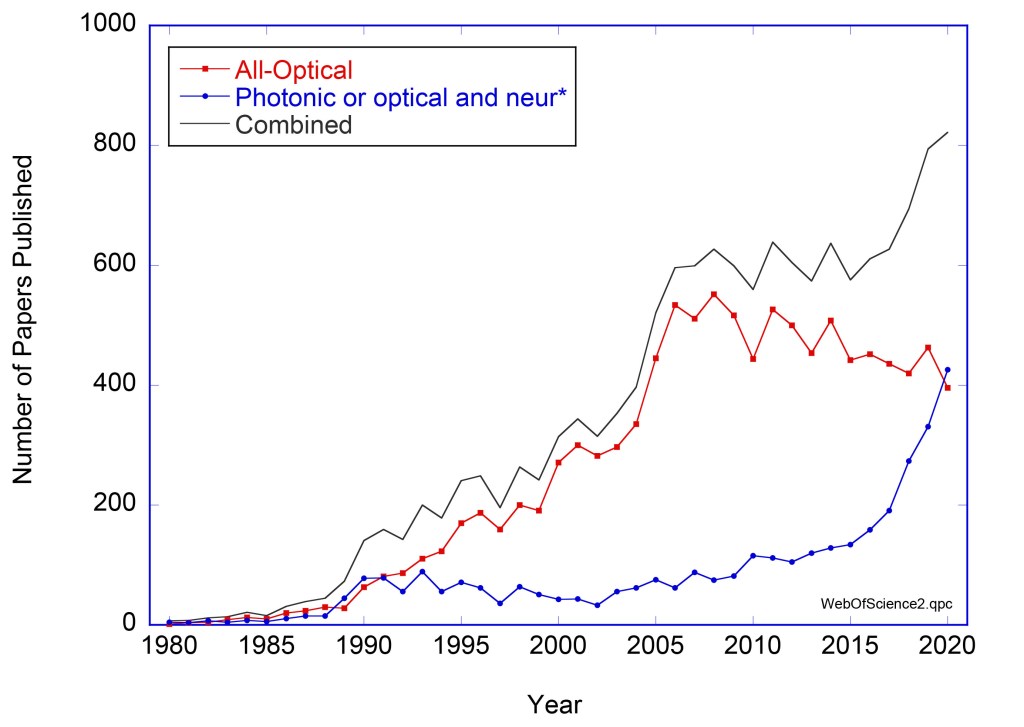
That said, it’s dangerous to ever say never, and research into all-optical computing and data processing is still going strong (See Fig. 1). It’s not the dream that was wrong, it was the time-scale that was wrong, just like fiber-to-the-home. Back in 2001, fiber-to-the-home was viewed as a pipe-dream by serious technology scouts. It took twenty years, but now that vision is coming true in urban settings. Back in 2001, all-optical computing seemed about 20 years away, but now it still looks 20 years out. Maybe this time the prediction is right. Recent advances in all-optical processing give some hope for it. Here are some of those advances.

Fig. 1 Number of papers published by year with the phrase in the title: “All-Optical” or “Photonic or Optical and Neur*” according to Web of Science search. The term “All-optical” saturated around 2005. Papers written around optical neural networks was low to 2015 but now is experiencing a strong surge. The sociology of title choices, and how favorite buzz words shift over time, can obscure underlying causes and trends, but overall there is current strong interest in all-optical systems.

The “What” and “Why” of All-Optical Processing

One of the great dreams of photonics is the use of light beams to perform optical logic in optical processors just as electronic currents perform electronic logic in transistors and integrated circuits.

Our information age, starting with the telegraph in the mid-1800’s, has been built upon electronics because the charge of the electron makes it a natural decision maker. Two charges attract or repel by Coulomb’s Law, exerting forces upon each other. Although we don’t think of currents acting in quite that way, the foundation of electronic logic remains electrical interactions.

But with these interactions also come constraints—constraining currents to be contained within wires, waiting for charging times that slow down decisions, managing electrical resistance and dissipation that generate heat (computer processing farms in some places today need to be cooled by glacier meltwater). Electronic computing is hardly a green technology.

Therefore, the advantages of optical logic are clear: broadcasting information without the need for expensive copper wires, little dissipation or heat, low latency (signals propagate at the speed of light). Furthermore, information on the internet is already in the optical domain, so why not keep it in the optical domain and have optical information packets making the decisions? All the routing and switching decisions about where optical information packets should go could be done by the optical packets themselves inside optical computers.

But there is a problem. Photons in free space don’t interact—they pass through each other unaffected. This is the opposite of what is needed for logic and decision making. The challenge of optical logic is then to find a way to get photons to interact.

Think of the scene in Star Wars: The New Hope when Obiwan Kenobi and Darth Vader battle to the death in a light saber duel—beams of light crashing against each other and repelling each other with equal and opposite forces. This is the photonic engineer’s dream! Light controlling light. But this cannot happen in free space. On the other hand, light beams can control other light beams inside nonlinear crystals where one light beam changes the optical properties of the crystal, hence changing how another light beam travels through it. These are nonlinear optical crystals.

Nonlinear Optics

Virtually all optical control designs, for any kind of optical logic or switch, require one light beam to affect the properties of another, and that requires an intervening medium that has nonlinear optical properties. The physics of nonlinear optics is actually simple: one light beam changes the electronic structure of a material which affects the propagation of another (or even the same) beam. The key parameter is the nonlinear coefficient that determines how intense the control beam needs to be to produce a significant modulation of the other beam. This is where the challenge is. Most materials have very small nonlinear coefficients, and the intensity of the control beam usually must be very high.

Therefore, to create low-power all-optical logic gates and switches there are four main design principles: 1) increase the nonlinear susceptibility by engineering the material, 2) increase the interaction length between the two beams, 3) concentrate light into small volumes, and 4) introduce feedback to boost the internal light intensities. Let’s take these points one at a time.

Nonlinear susceptibility: The key to getting stronger interaction of light with light is in the ease with which a control beam of light can distort the crystal so that the optical conditions change for a signal beam. This is called the nonlinear susceptibility . When working with “conventional” crystals like semiconductors (e.g. CdZnSe) or rare-Earths (e.g. LiNbO₃), there is only so much engineering that is possible to try to tweak the nonlinear susceptibilities. However, artificially engineered materials can offer significant increases in nonlinear susceptibilities, these include plasmonic materials, metamaterials, organic semiconductors, photonic crystals. An increasingly important class of nonlinear optical devices are semiconductor optical amplifiers (SOA).

Interaction length: The interaction strength between two light waves is a product of the nonlinear polarization and the length over which the waves interact. Interaction lengths can be made relatively long in waveguides but can be made orders of magnitude longer in fibers. Therefore, nonlinear effects in fiber optics are a promising avenue for achieving optical logic.

Intensity Concentration: Nonlinear polarization is the product of the nonlinear susceptibility with the field amplitude of the waves. Therefore, focusing light down to small cross sections produces high power, as in the core of a fiber optic, again showing advantages of fibers for optical logic implementations.

Feedback: Feedback, as in a standing-wave cavity, increases the intensity as well as the effective interaction length by folding the light wave continually back on itself. Both of these effects boost the nonlinear interaction, but then there is an additional benefit: interferometry. Cavities, like a Fabry-Perot, are interferometers in which a slight change in the round-trip phase can produce large changes in output light intensity. This is an optical analog to a transistor in which a small control current acts as a gate for an exponential signal current. The feedback in the cavity of a semiconductor optical amplifier (SOA), with high internal intensities and long effective interaction lengths and an active medium with strong nonlinearity make these elements attractive for optical logic gates. Similarly, integrated ring resonators have the advantage of interferometric control for light switching. Many current optical switches and logic gates are based on SOAs and integrated ring resonators.

All-Optical Regeneration

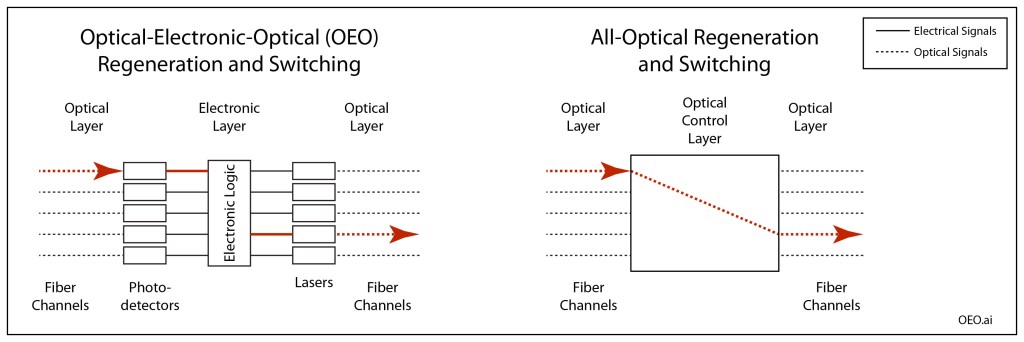
The vision of the all-optical internet, where the logic operations that direct information to different locations is all performed by optical logic without ever converting into the electrical domain, is facing a barrier that is as challenging to overcome today as it was back in 2001: all-optical regeneration. All-optical regeneration has been and remains the Achilles Heal of the all-optical internet.

Signal regeneration is currently performed through OEO conversion: Optical-to-Electronic-to-Optical. In OEO conversion, a distorted signal (distortion is caused by attenuation and dispersion and noise as signals travel down fiber optics) is received by a photodetector, is interpreted as ones and zeros that drive laser light sources that launch the optical pulses down the next stretch of fiber. The new pulses are virtually perfect, but they again degrade as they travel, until they are regenerated, and so on. The added advantage of the electrical layer is that the electronic signals can be used to drive conventional electronic logic for switching.

In all-optical regeneration, on the other hand, the optical pulses need to be reamplified, reshaped and retimed––known as 3R regeneration––all by sending the signal pulses through nonlinear amplifiers and mixers, which may include short stretches of highly nonlinear fiber (HNLF) or semiconductor optical amplifiers (SOA). There have been demonstrations of 2R all-optical regeneration (reamplifying and reshaping but not retiming) at lower data rates, but getting all 3Rs at the high data rates (40 Gb/s) in the next generation telecom systems remains elusive.

Nonetheless, there is an active academic literature that is pushing the envelope on optical logical devices and regenerators [1]. Many of the systems focus on SOA’s, HNLF’s and Interferometers. Numerical modeling of these kinds of devices is currently ahead of bench-top demonstrations, primarily because of the difficulty of fabrication and device lifetime. But the numerical models point to performance that would be competitive with OEO. If this OOO conversion (Optical-to-Optical-to-Optical) is scalable (can handle increasing bit rates and increasing numbers of channels), then the current data crunch that is facing the telecom trunk lines (see my previous Blog) may be a strong driver to implement such all-optical solutions.

It is important to keep in mind that legacy technology is not static but also continues to improve. As all-optical logic and switching and regeneration make progress, OEO conversion gets incrementally faster, creating a moving target. Therefore, we will need to wait another 20 years to see whether OEO is overtaken and replaced by all-optical.

*Fig. 3 Optical-Electronic-Optical regeneration and switching compared to all-optical control. The optical control is performed using SOA’s, interferometers and nonlinear fibers.*

Photonic Neural Networks

The most exciting area of optical logic today is in analog optical computing––specifically optical neural networks and photonic neuromorphic computing [2, 3]. A neural network is a highly-connected network of nodes and links in which information is distributed across the network in much the same way that information is distributed and processed in the brain. Neural networks can take several forms––from digital neural networks that are implemented with software on conventional digital computers, to analog neural networks implemented in specialized hardware, sometimes also called neuromorphic computing systems.

Optics and photonics are well suited to the analog form of neural network because of the superior ability of light to form free-space interconnects (links) among a high number of optical modes (nodes). This essential advantage of light for photonic neural networks was first demonstrated in the mid-1980’s using recurrent neural network architectures implemented in photorefractive (nonlinear optical) crystals (see Fig. 1 for a publication timeline). But this initial period of proof-of-principle was followed by a lag of about 2 decades due to a mismatch between driver applications (like high-speed logic on an all-optical internet) and the ability to configure the highly complex interconnects needed to perform the complex computations.

Fig. 4 Optical vector-matrix multiplication. An LED array is the input vector, focused by a lens onto the spatial light modulator that is the 2D matrix. The transmitted light is refocussed by the lens onto a photodiode array with is the output vector. Free-space propagation and multiplication is a key advantage to optical implementation of computing.

The rapid rise of deep machine learning over the past 5 years has removed this bottleneck, and there has subsequently been a major increase in optical implementations of neural networks. In particular, it is now possible to use conventional deep machine learning to design the interconnects of analog optical neural networks for fixed tasks such as image recognition [4]. At first look, this seems like a non-starter, because one might ask why not use the conventional trained deep network to do the recognition itself rather than using it to create a special-purpose optical recognition system. The answer lies primarily in the metrics of latency (speed) and energy cost.

In neural computing, approximately 90% of the time and energy go into matrix multiplication operations. Deep learning algorithms driving conventional digital computers need to do the multiplications at the sequential clock rate of the computer using nested loops. Optics, on the other had, is ideally suited to perform matrix multiplications in a fully parallel manner (see Fig. 4). In addition, a hardware implementation using optics operates literally at the speed of light. The latency is limited only by the time of flight through the optical system. If the optical train is 1 meter, then the time for the complete computation is only a few nanoseconds at almost no energy dissipation. Combining the natural parallelism of light with the speed has led to unprecedented computational rates. For instance, recent implementations of photonic neural networks have demonstrated over 10 Trillion operations per second (TOPS) [5].

It is important to keep in mind that although many of these photonic neural networks are characterized as all-optical, they are generally not reconfigurable, meaning that they are not adaptive to changing or evolving training sets or changing input information. Most adaptive systems use OEO conversion with electronically-addressed spatial light modulators (SLM) that are driven by digital logic. Another technology gaining recent traction is neuromorphic photonics in which neural processing is implemented on photonic integrated circuits (PICS) with OEO conversion. The integration of large numbers of light emitting sources on PICs is now routine, relieving the OEO bottleneck as electronics and photonics merge in silicon photonics.

Farther afield are all-optical systems that are adaptive through the use of optically-addressed spatial light modulators or nonlinear materials. In fact, these types of adaptive all-optical neural networks were among the first demonstrated in the late 1980’s. More recently, advanced adaptive optical materials, as well as fiber delay lines for a type of recurrent neural network known as reservoir computing, have been used to implement faster and more efficient optical nonlinearities needed for adaptive updates of neural weights. But there are still years to go before light is adaptively controlling light entirely in the optical domain at the speeds and with the flexibility needed for real-world applications like photonic packet switching in telecom fiber-optic routers.

In stark contrast to the status of classical all-optical computing, photonic quantum computing is on the cusp of revolutionizing the field of quantum information science. The recent demonstration from the Canadian company Xanadu of a programmable photonic quantum computer that operates at room temperature may be the harbinger of what is to come in the third generation Machines of Light: Quantum Optical Computers, which is the topic of my next blog.

By David D. Nolte, Nov. 28, 2021

Twenty Years at Light Speed: Fiber Optics and the Future of the Photonic Internet

Twenty years ago this November, my book Mind at Light Speed: A New Kind of Intelligence was published by The Free Press (Simon & Schuster, 2001). The book described the state of optical science at the turn of the Millennium through three generations of Machines of Light: The Optoelectronic Generation of electronic control meshed with photonic communication; The All-Optical Generation of optical logic; and The Quantum Optical Generation of quantum communication and computing.

To mark the occasion of the publication, this Blog Post begins a three-part series that updates the state-of-the-art of optical technology, looking at the advances in optical science and technology over the past 20 years since the publication of Mind at Light Speed. This first blog reviews fiber optics and the photonic internet. The second blog reviews all-optical communication and computing. The third and final blog reviews the current state of photonic quantum communication and computing.

The Wabash Yacht Club

During late 1999 and early 2000, while I was writing Mind at Light Speed, my wife Laura and I would often have lunch at the ironically-named Wabash Yacht Club. Not only was it not a Yacht Club, but it was a dark and dingy college-town bar located in a drab 70-‘s era plaza in West Lafayette, Indiana, far from any navigable body of water. But it had a great garlic burger and we loved the atmosphere.

The Wabash River. No yachts. (https://www.riverlorian.com/wabash-river)

One of the TV monitors in the bar was always tuned to a station that covered stock news, and almost every day we would watch the NASDAQ rise 100 points just over lunch. This was the time of the great dot-com stock-market bubble—one of the greatest speculative bubbles in the history of world economics. In the second quarter of 2000, total US venture capital investments exceeded $30B as everyone chased the revolution in consumer market economics.

Fiber optics will remain the core technology of the internet for the foreseeable future.

Part of that dot-com bubble was a massive bubble in optical technology companies, because everyone knew that the dot-com era would ride on the back of fiber optics telecommunications. Fiber optics at that time had already revolutionized transatlantic telecommunications, and there seemed to be no obstacle for it to do the same land-side with fiber optics to every home bringing every dot-com product to every house and every movie ever made. What would make this possible was the tremendous information bandwidth that can be crammed into tiny glass fibers in the form of photon packets traveling at the speed of light.

Doing optics research at that time was a heady experience. My research on real-time optical holography was only on the fringe of optical communications, but at the CLEO conference on lasers and electro-optics, I was invited by tiny optics companies to giant parties, like a fully-catered sunset cruise on a schooner sailing Baltimore’s inner harbor. Venture capital scouts took me to dinner in San Francisco with an eye to scoop up whatever patents I could dream of. And this was just the side show. At the flagship fiber-optics conference, the Optical Fiber Conference (OFC) of the OSA, things were even crazier. One tiny company that made a simple optical switch went almost overnight from a company worth a couple of million to being bought out by Nortel (the giant Canadian telecommunications conglomerate of the day) for over 4 billion dollars.

The Telecom Bubble and Bust

On the other side from the small mom-and-pop optics companies were the giants like Corning (who made the glass for the glass fiber optics) and Nortel. At the height of the telecom bubble in September 2000, Nortel had a capitalization of almost $400B Canadian dollars due to massive speculation about the markets around fiber-optic networks.

One of the central questions of the optics bubble of Y2K was what the new internet market would look like. Back then, fiber was only beginning to connect to distribution nodes that were connected off the main cross-country trunk lines. Cable TV dominated the market with fixed programming where you had to watch whatever they transmitted whenever they transmitted it. Google was only 2 years old, and Youtube didn’t even exist then—it was founded in 2005. Everyone still shopped at malls, while Amazon had only gone public three years before.

There were fortune tellers who predicted that fiber-to-the-home would tap a vast market of online commerce where you could buy anything you wanted and have it delivered to your door. They foretold of movies-on-demand, where anyone could stream any movie they wanted at any time. They also foretold of phone calls and video chats that never went over the phone lines ruled by the telephone monopolies. The bandwidth, the data rates, that these markets would drive were astronomical. The only technology at that time that could support such high data rates was fiber optics.

At first, these fortune tellers drove an irrational exuberance. But as the stocks inflated, there were doomsayers who pointed out that the costs at that time of bringing fiber into homes was prohibitive. And the idea that people would be willing to pay for movies-on-demand was laughable. The cost of the equipment and the installation just didn’t match what then seemed to be a sparse market demand. Furthermore, the fiber technology in the year 2000 couldn’t even get to the kind of data rates that could support these dreams.

In March of 2000 the NASDAQ hit a high of 5000, and then the bottom fell out.

By November 2001 the NASDAQ had fallen to 1500. One of the worst cases of the telecom bust was Nortel whose capitalization plummeted from $400B at its high to $5B Canadian by August 2002. Other optics companies fared little better.

The main questions, as we stand now looking back from 20 years in the future, are: What in real life motivated the optics bubble of 2000? And how far has optical technology come since then? The surprising answer is that the promise of optics in 2000 was not wrong—the time scale was just off.

Fiber to the Home

Today, fixed last-mile broadband service is an assumed part of life in metro areas in the US. This broadband takes on three forms: legacy coaxial cable, 4G wireless soon to be upgraded to 5G, and fiber optics. There are arguments pro and con for each of these technologies, especially moving forward 10 or 20 years or more, and a lot is at stake. The global market revenue was $108 Billion in 2020 and is expected to reach $200 Billion in 2027, growing at over 9% from 2021 to 2027.

To sort through the pros and cons to pick the wining technology, several key performance parameters must be understood for each technology. The two most important performance measures are bandwidth and latency. Bandwidth is the data rate—how many bits per second can you get to the home. Latency is a little more subtle. It is the time it takes to complete a transmission. This time includes the actual time for information to travel from a transmitter to a receiver, but that is rarely the major contributor. Currently, almost all of the latency is caused by the logical operations needed to move the information onto and off of the home data links.

Coax (short for coaxial cable) is attractive because so much of the last-mile legacy hardware is based on the old cable services. But coax cable has very limited bandwidth and high latency. As a broadband technology, it is slowly disappearing.

Wireless is attractive because the information is transmitted in the open air without any need for physical wires or fibers. But high data rates require high frequency. For instance, 4G wireless operates at frequencies between 700 MHz to 2.6 GHz. Current WiFi is 2.4 GHz or 5 GHz, and next-generation 5G will have 26 GHz using millimeter wave technology, and WiGig is even more extreme at 60 GHz. While WiGig will deliver up to 10 Gbits per second, as everyone with wireless routers in their homes knows, the higher the frequency, the more it is blocked by walls or other obstacles. Even 5 GHz is mostly attenuated by walls, and the attenuation gets worse as the frequency gets higher. Testing of 5G networks has shown that cell towers need to be closely spaced to allow seamless coverage. And the crazy high frequency of WiGig all but guarantees that it will only be usable for line-of-sight communication within a home or in an enterprise setting.

Fiber for the last mile, on the other hand, has multiple advantages. Chief among these is that fiber is passive. It is a light pipe that has ten thousand times more usable bandwidth than a coaxial cable. For instance, lab tests have pushed up to 100 Tbit/sec over kilometers of fiber. To access that bandwidth, the input and output hardware can be continually upgraded, while the installed fiber is there to handle pretty much any amount of increasing data rates for the next 10 or 20 years. Fiber installed today is supporting 1 Gbit/sec data rates, and the existing protocol will work up to 10 Gbit/sec—data rates that can only be hoped for with WiFi. Furthermore, optical communications on fiber have latencies of around 1.5 msec over 20 kilometers compared with 4G LTE that has a latency of 8 msec over 1 mile. The much lower latency is key to support activities that cannot stand much delay, such as voice over IP, video chat, remote controlled robots, and virtual reality (i.e., gaming). On top of all of that, the internet technology up to the last mile is already almost all optical. So fiber just extends the current architecture across the last mile.

Therefore, fixed fiber last-mile broadband service is a technology winner. Though the costs can be higher than for WiFi or coax in the short run for installation, the long-run costs are lower when amortized over the lifetime of the installed fiber which can exceed 25 years.

It is becoming routine to have fiber-to-the-curb (FTTC) where a connection box converts photons in fibers into electrons on copper to take the information into the home. But a market also exists in urban settings for fiber-to-the-home (FTTH) where the fiber goes directly into the house to a receiver and only then would the information be converted from photons to electrons and electronics.

Shortly after Mind at Light Speed was published in 2001, I was called up by a reporter for the Seattle Times who wanted to know my thoughts about FTTH. When I extolled its virtue, he nearly hung up on me. He was in the middle of debunking the telecom bubble and his premise was that FTTH was a fraud. In 2001 he might have been right. But in 2021, FTTH is here, it is expanding, and it will continue to do so for at least another quarter century. Fiber to the home will become the legacy that some future disruptive technology will need to displace.

*Fig. 1 Optical data rates on optical links, trunk lines and submarine cables over the past 30 years and projecting into the future. Redrawn from Refs. [1, 2]*

Trunk-Line Fiber Optics

Despite the rosy picture for Fiber to the Home, a storm is brewing for the optical trunk lines. The total traffic on the internet topped a billion Terrabytes in 2019 and is growing fast, doubling about every 2 years on an exponential growth curve. In 20 years, that becomes another factor of a thousand more traffic in 2040 than today. Therefore, the technology companies that manage and supply the internet worry about a capacity crunch that is fast approaching when there will be more demand than the internet can supply.

Over the past 20 years, the data rates on the fiber trunk lines—the major communication links that span the United States—matched demand by packing more bits in more ways into the fibers. Up to 2009, increased data rates were achieved using dispersion-managed wavelength-division multiplexing (WDM) which means that they kept adding more lasers of slightly different colors to send the optical bits down the fiber. For instance, in 2009 the commercial standard was 80 colors each running at 40 Gbit/sec for a total of 3.2 Tbit/sec down a single fiber.

Since 2009, increased bandwidth has been achieved through coherent WDM, where not only the amplitude of light but also the phase of the light is used to encode bits of information using interferometry. We are still in the coherent WDM era as improved signal processing is helping to fill the potential coherent bandwidth of a fiber. Commercial protocols using phase-shift keying, quadrature phase-shift keying, and 16-quadrature amplitude modulation currently support 50 Gbit/sec, 100 Gbit/sec and 200 Gbit/sec, respectively. But the capacity remaining is shrinking, and several years from now, a new era will need to begin in order to keep up with demand. But if fibers are already using time, color, polarization and phase to carry information, what is left?

The answer is space!

Coming soon will be commercial fiber trunk lines that use space-division multiplexing (SDM). The simplest form is already happening now as fiber bundles are replacing single-mode fibers. If you double the number of fibers in a cable, then you double the data rate of the cable. But the problem with this simple approach is the scaling. If you double just 10 times, then you need 1024 fibers in a single cable—each fiber needing its own hardware to launch the data and retrieve it at the other end. This is linear scaling, which is bad scaling for commercial endeavors.

Fig. 2 Fiber structures for space-division multiplexing (SDM). Fiber bundles are cables of individual single-mode fibers. Multi-element fibers (MEF) are single-mode fibers formed together inside the coating. Multi-core fibers (MCF) have multiple cores within the cladding. Few-mode fibers (FMF) are multi-mode fibers with small mode numbers. Coupled core (CC) fibers are multi-core fibers in which the cores are close enough that the light waves are coupled into coupled spatial modes. Redrawn from Ref. [3]

Therefore, alternatives for tapping into SDM are being explored in lab demonstrations now that have sublinear scaling (costs don’t rise as fast as improved capacity). These include multi-element fibers where multiple fiber optical elements are manufactured as a group rather than individually and then combined into a cable. There are also multi-core fibers, where multiple fibers share the same cladding. These approaches provide multiple fibers for multiple channels without a proportional rise in cost.

More exciting are approaches that use few-mode-fibers (FMF) to support multiple spatial modes traveling simultaneously down the same fiber. In the same vein are coupled-core fibers which is a middle ground between multi-core fibers and few-mode fibers in that individual cores can interact within the cladding to support coupled spatial modes that can encode separate spatial channels. Finally, combinations of approaches can use multiple formats. For instance, a recent experiment combined FMF and MCF that used 19 cores each supporting 6 spatial modes for a total of 114 spatial channels.

However, space-division multiplexing has been under development for several years now, yet it has not fully moved into commercial systems. This may be a sign that the doubling rate of bandwidth may be starting to slow down, just as Moore’s Law slowed down for electronic chips. But there were doomsayers foretelling the end of Moore’s Law for decades before it actually slowed down, because new ideas cannot be predicted. But even if the full capacity of fiber is being approached, there is certainly nothing that will replace fiber with any better bandwidth. So fiber optics will remain the core technology of the internet for the foreseeable future.

But what of the other generations of Machines of Light: the all-optical and the quantum-optical generations? How have optics and photonics fared in those fields? Stay tuned for my next blogs to find out.

By David D. Nolte, Nov. 8, 2021

Bibliography

[1] P. J. Winzer, D. T. Neilson, and A. R. Chraplyvy, “Fiber-optic transmission and networking: the previous 20 and the next 20 years,” Optics Express, vol. 26, no. 18, pp. 24190-24239, Sep (2018) [Link]

[2] W. Shi, Y. Tian, and A. Gervais, “Scaling capacity of fiber-optic transmission systems via silicon photonics,” Nanophotonics, vol. 9, no. 16, pp. 4629-4663, Nov (2020)

10.1515_nanoph-2020-0309 Download

[3] E. Agrell, M. Karlsson, A. R. Chraplyvy, D. J. Richardson, P. M. Krummrich, P. Winzer, K. Roberts, J. K. Fischer, S. J. Savory, B. J. Eggleton, M. Secondini, F. R. Kschischang, A. Lord, J. Prat, I. Tomkos, J. E. Bowers, S. Srinivasan, M. Brandt-Pearce, and N. Gisin, “Roadmap of optical communications,” Journal of Optics, vol. 18, no. 6, p. 063002, 2016/05/04 (2016) [Link]

June 3, 2021November 26, 2023 by David D. Nolte

The Transverse Doppler Effect and Relativistic Time Dilation

One of the hardest aspects to grasp about relativity theory is the question of whether an event “looks as if” it is doing something, or whether it “actually is” doing something.

Take, for instance, the classic twin paradox of relativity theory in which there are twins who wear identical high-precision wrist watches. One of them rockets off to Alpha Centauri at relativistic speeds and returns while the other twin stays on Earth. Each twin sees the other twin’s clock running slowly because of relativistic time dilation. Yet when they get back together and, standing side-by-side, they compare their watches—the twin who went to Alpha Centauri is actually younger than the other, despite the paradox. The relativistic effect of time dilation is “real”, not just apparent, regardless of whether they come back together to do the comparison.

Yet this understanding of relativistic effects took many years, even decades, to gain acceptance after Einstein proposed them. He was aware himself that key experiments were required to prove that relativistic effects are real and not just apparent.

Einstein and the Transverse Doppler Effect

In 1905 Einstein used his new theory of special relativity to predict observable consequences that included relativistic velocity addition and a general treatment of the relativistic Doppler effect [1]. This included the effects of time dilation in addition to the longitudinal effect of the source chasing the wave. Time dilation produced a correction to Doppler’s original expression for the longitudinal effect that became significant at speeds approaching the speed of light. More significantly, it predicted a transverse Doppler effect for a source moving along a line perpendicular to the line of sight to an observer. This effect had not been predicted either by Christian Doppler (1803 – 1853) or by Woldemar Voigt (1850 – 1919).

( Read article in Physics Today on the history of the Doppler effect [2] )

Despite the generally positive reception of Einstein’s theory of special relativity, some of its consequences were anathema to many physicists at the time. A key stumbling block was the question whether relativistic effects, like moving clocks running slowly, were only apparent, or were actually real, and Einstein had to fight to convince others of its reality. When Johannes Stark (1874 – 1957) observed Doppler line shifts in ion beams called “canal rays” in 1906 (Stark received the 1919 Nobel prize in part for this discovery) [3], Einstein promptly published a paper suggesting how the canal rays could be used in a transverse geometry to directly detect time dilation through the transverse Doppler effect [4]. Thirty years passed before the experiment was performed with sufficient accuracy by Herbert Ives and G. R. Stilwell in 1938 to measure the transverse Doppler effect [5]. Ironically, even at this late date, Ives and Stilwell were convinced that their experiment had disproved Einstein’s time dilation by supporting Lorentz’ contraction theory of the electron. The Ives-Stilwell experiment was the first direct test of time dilation, followed in 1940 by muon lifetime measurements [6].

A) Transverse Doppler Shift Relative to Emission Angle

The Doppler effect varies between blue shifts in the forward direction to red shifts in the backward direction, with a smooth variation in Doppler shift as a function of the emission angle. Consider the configuration shown in Fig. 1 for light emitted from a source moving at speed v and emitting at an angle θ₀ in the receiver frame. The source moves a distance vT in the time of a single emission cycle (assume a harmonic wave). In that time T (which is the period of oscillation of the light source — or the period of a clock if we think of it putting out light pulses) the light travels a distance cT before another cycle begins (or another pulse is emitted).

Fig. 1 Configuration for detection of Doppler shifts for emission angle θ₀. The light source travels a distance vT during the time of a single cycle, while the wavefront travels a distance cT towards the detector.

[ See YouTube video on the derivation of the transverse Doppler Effect.]

The observed wavelength in the receiver frame is thus given by

where T is the emission period of the moving source. Importantly, the emission period is time dilated relative to the proper emission time of the source

Therefore,

This expression can be evaluated for several special cases:

a) θ₀ = 0 for forward emission

which is the relativistic blue shift for longitudinal motion in the direction of the receiver.

b) θ₀ = π for backward emission

which is the relativistic red shift for longitudinal motion away from the receiver

c) θ₀ = π/2 for transverse emission

This transverse Doppler effect for emission at right angles is a red shift, caused only by the time dilation of the moving light source. This is the effect proposed by Einstein and observed by Stark that proved moving clocks tick slowly. But it is not the only way to view the transverse Doppler effect.

B) Transverse Doppler Shift Relative to Angle at Reception

A different option for viewing the transverse Doppler effect is the angle to the moving source at the moment that the light is detected. The geometry of this configuration relative to the previous is illustrated in Fig. 2.

Fig. 2 The detection point is drawn at a finite distance. However, the relationship between θ₀ and θ₁ is independent of the distance to the detector

The transverse distance to the detection point is

The length of the line connecting the detection point P with the location of the light source at the moment of detection is (using the law of cosines)

Combining with the first equation gives

An equivalent expression is obtained as

Note that this result, relating θ₁ to θ₀, is independent of the distance to the observation point.

When θ₁ = π/2, then

yielding

for which the Doppler effect is

which is a blue shift. This creates the unexpected result that sin θ₀ = π/2 produces a red shift, while sin θ₁ = π/2 produces a blue shift. The question could be asked: which one represents time dilation? In fact, it is sin θ₀ = π/2 that produces time dilation exclusively, because in that configuration there is no foreshortening effect on the wavelength–only the emission time.

C) Compromise: The Null Transverse Doppler Shift

The previous two configurations each could be used as a definition for the transverse Doppler effect. But one gives a red shift and one gives a blue shift, which seems contradictory. Therefore, one might try to strike a compromise between these two cases so that sin θ₁ = sin θ₀, and the configuration is shown in Fig. 3.

This is the case when θ₁ + θ₂ = π. The sines of the two angles are equal, yielding

and

which is solved for

Inserting this into the Doppler equation gives

where the Taylor’s expansion of the denominator (at low speed) cancels the numerator to give zero net Doppler shift. This compromise configuration represents the condition of null Doppler frequency shift. However, for speeds approaching the speed of light, the net effect is a lengthening of the wavelength, dominated by time dilation, causing a red shift.

D) Source in Circular Motion Around Receiver

An interesting twist can be added to the problem of the transverse Doppler effect: put the source or receiver into circular motion, one about the other. In the case of a source in circular motion around the receiver, it is easy to see that this looks just like case A) above for θ₀ = π/2, which is the red shift caused by the time dilation of the moving source

However, there is the possible complication that the source is no longer in an inertial frame (it experiences angular acceleration) and therefore it is in the realm of general relativity instead of special relativity. In fact, it was Einstein’s solution to this problem that led him to propose the Equivalence Principle and make his first calculations on the deflection of light by gravity. His solution was to think of an infinite number of inertial frames, each of which was instantaneously co-moving with the same linear velocity as the source. These co-moving frames are inertial and can be analyzed using the principles of special relativity. The general relativistic effects come from slipping from one inertial co-moving frame to the next. But in the case of the circular transverse Doppler effect, each instantaneously co-moving frame has the exact configuration as case A) above, and so the wavelength is red shifted exactly by the time dilation.

Fig. Left: Moving source around a stationary receiver has red-shifted light (pure time dilation effect). Right. Moving receiver around a stationary source has blue-shifted light.

E) Receiver in Circular Motion Around Source

Now flip the situation and consider a moving receiver orbiting a stationary source.

With the notion of co-moving inertial frames now in hand, this configuration is exactly the same as case B) above, and the wavelength is blue shifted according to the equation

caused by foreshortening.

By David D. Nolte, June 3, 2021

New from Oxford Press: The History of Light and Interference (2023)

Read about the physics and history of light and optics.

Available at Amazon

Available at Oxford

Available at Barnes&Noble

References

[1] A. Einstein, “On the electrodynamics of moving bodies,” Annalen Der Physik, vol. 17, no. 10, pp. 891-921, Sep (1905)

[2] D. D. Nolte, “The Fall and Rise of the Doppler Effect,” Physics Today, vol. 73, no. 3, pp. 31-35, Mar (2020)

[3] J. Stark, W. Hermann, and S. Kinoshita, “The Doppler effect in the spectrum of mercury,” Annalen Der Physik, vol. 21, pp. 462-469, Nov 1906.

[4] A. Einstein, “Possibility of a new examination of the relativity principle,” Annalen Der Physik, vol. 23, no. 6, pp. 197-198, May (1907)

[5] H. E. Ives and G. R. Stilwell, “An experimental study of the rate of a moving atomic clock,” Journal of the Optical Society of America, vol. 28, p. 215, 1938.

[6] B. Rossi and D. B. Hall, “Variation of the Rate of Decay of Mesotrons with Momentum,” Physical Review, vol. 59, pp. 223–228, 1941.

April 5, 2021August 16, 2025 by David D. Nolte

The Lens of Gravity: Einstein’s Rings

Einstein’s theory of gravity came from a simple happy thought that occurred to him as he imagined an unfortunate worker falling from a roof, losing hold of his hammer, only to find both the hammer and himself floating motionless relative to each other as if gravity had ceased to exist. With this one thought, Einstein realized that the falling (i.e. accelerating) reference frame was in fact an inertial frame, and hence all the tricks that he had learned and invented to deal with inertial relativistic frames could apply just as well to accelerating frames in gravitational fields.

Gravitational lensing (and microlensing) have become a major tool of discovery in astrophysics applied to the study of quasars, dark matter and even the search for exoplanets.

Armed with this new perspective, one of the earliest discoveries that Einstein made was that gravity must bend light paths. This phenomenon is fundamentally post-Newtonian, because there can be no possible force of gravity on a massless photon—yet Einstein’s argument for why gravity should bend light is so obvious that it is manifestly true, as demonstrated by Arthur Eddington during the solar eclipse of 1919, launching Einstein to world-wide fame. It is also demonstrated by the beautiful gravitational lensing phenomenon of Einstein arcs. Einstein arcs are the distorted images of bright distant light sources in the universe caused by an intervening massive object, like a galaxy or galaxy cluster, that bends the light rays. A number of these arcs are seen in images of the Abel cluster of galaxies in Fig. 1.

Fig. 1 Numerous Einstein arcs seen in the Abel cluster of galaxies.

Gravitational lensing (and microlensing) have become a major tool of discovery in astrophysics applied to the study of quasars, dark matter and even the search for exoplanets. However, as soon as Einstein conceived of gravitational lensing, in 1912, he abandoned the idea as too small and too unlikely to ever be useful, much like he abandoned the idea of gravitational waves in 1915 as similarly being too small ever to detect. It was only at the persistence of an amateur Czech scientist twenty years later that Einstein reluctantly agreed to publish his calculations on gravitational lensing.

The History of Gravitational Lensing

In 1912, only a few years after his “happy thought”, and fully three years before he published his definitive work on General Relativity, Einstein derived how light would be affected by a massive object, causing light from a distant source to be deflected like a lens. The historian of physics, Jürgen Renn discovered these derivations in Einstein’s notebooks while at the Max Planck Institute for the History of Science in Berlin in 1996 [1]. However, Einstein also calculated the magnitude of the effect and dismissed it as too small, and so he never published it.

Years later, in 1936, Einstein received a visit from a Czech electrical engineer Rudi Mandl, an amateur scientist who had actually obtained a small stipend from the Czech government to visit Einstein at the Institute for Advanced Study at Princeton. Mandl had conceived of the possibility of gravitational lensing and wished to bring it to Einstein’s attention, thinking that the master would certainly know what to do with the idea. Einstein was obliging, redoing his calculations of 1912 and obtaining once again the results that made him believe that the effect would be too small to be seen. However, Mandl was persistent and pressed Einstein to publish the results, which he did [2]. In his submission letter to the editor of Science, Einstein stated “Let me also thank you for your cooperation with the little publication, which Mister Mandl squeezed out of me. It is of little value, but it makes the poor guy happy”. Einstein’s pessimism was based on his thinking that isolated stars would be the only source of the gravitational lens (he did not “believe” in black holes), but in 1937 Fritz Zwicky at Cal Tech (a gadfly genius) suggested that the newly discovered phenomenon of “galaxy clusters” might provide the massive gravity that would be required to produce the effect. Although, to be visible, a distant source would need to be extremely bright.

Potential sources were discovered in the 1960’s using radio telescopes that discovered quasi-stellar objects (known as quasars) that are extremely bright and extremely far away. Quasars also appear in the visible range, and in 1979 a twin quasar was discovered by astronomers using the telescope at the Kitt Peak Obversvatory in Arizona–two quasars very close together that shared identical spectral fingerprints. The astronomers realized that it could be a twin image of a single quasar caused by gravitational lensing, which they published as a likely explanation. Although the finding was originally controversial, the twin-image was later confirmed, and many additional examples of gravitational lensing have since been discovered.

The Optics of Gravity and Light

Gravitational lenses are terrible optical instruments. A good imaging lens has two chief properties: 1) It produces increasing delay on a wavefront as the radial distance from the optic axis decreases; and 2) it deflects rays with increasing deflection angle as the radial distance of a ray increases away from the optic axis (the center of the lens). Both properties are part of the same effect: the conversion, by a lens, of an incident plane wave into a converging spherical wave. A third property of a good lens ensures minimal aberrations of the converging wave: a quadratic dependence of wavefront delay on radial distance from the optic axis. For instance, a parabolic lens produces a diffraction-limited focal spot.

Now consider the optical effects of gravity around a black hole. One of Einstein’s chief discoveries during his early investigations into the effects of gravity on light is the analogy of warped space-time as having an effective refractive index. Light propagates through space affected by gravity as if there were a refractive index associated with the gravitational potential. In a previous blog on the optics of gravity, I showed the simple derivation of the refractive effects of gravity on light based on the Schwarschild metric applied to a null geodesic of a light ray. The effective refractive index near a black hole is

This effective refractive index diverges at the Schwarzschild radius of the black hole. It produces the maximum delay, not on the optic axis as for a good lens, but at the finite distance R_S. Furthermore, the maximum deflection also occurs at R_S, and the deflection decreases with increasing radial distance. Both of these properties of gravitational lensing are opposite to the properties of a good lens. For this reason, the phrase “gravitational lensing” is a bit of a misnomer. Gravitating bodies certainly deflect light rays, but the resulting optical behavior is far from that of an imaging lens.

The path of a ray from a distant quasar, through the thin gravitational lens of a galaxy, and intersecting the location of the Earth, is shown in Fig. 2. The location of the quasar is a distance R from the “optic axis”. The un-deflected angular position is θ₀, and with the intervening galaxy the image appears at the angular position θ. The angular magnification is therefore M = θ/θ₀.

Fig. 2 Optical ray layout for gravitational lensing and Einstein rings. All angles are greatly exaggerated; typical angles are in the range of several arcseconds.

The deflection angles are related through

where b is the “impact parameter”

These two equations are solved to give to an expression that relates the unmagnified angle θ₀ to the magnified angle θ as

where

is the angular size of the Einstein ring when the source is on the optic axis. The quadratic equation has two solutions that gives two images of the distant quasar. This is the origin of the “double image” that led to the first discovery of gravitational lensing in 1979.

When the distant quasar is on the optic axis, then θ₀ = 0 and the deflection of the rays produces, not a double image, but an Einstein ring with an angular size of θ_E. For typical lensing objects, the angular size of Einstein rings are typically in the range of tens of microradians. The angular magnification for decreasing distance R diverges as

But this divergence is more a statement of the bad lens behavior than of actual image size. Because the gravitational lens is inverted (with greater deflection closer to the optic axis) compared to an ideal thin lens, it produces a virtual image ring that is closer than the original object, as in Fig. 3.

Fig. 3 Gravitational lensing does not produce an “image” but rather an Einstein ring that is virtual and magnified (appears closer).

The location of the virtual image behind the gravitational lens (when the quasar is on the optic axis) is obtained from

If the quasar is much further from the lens than the Earth, then the image location is z_i = -L₁, or behind the lens by the same distance from the Earth to the lens. The longitudinal magnification is then

Note that while the transverse (angular) magnification diverges as the object approaches the optic axis, the longitudinal magnification remains finite but always greater than unity.

The Caustic Curves of Einstein Rings

Because gravitational lenses have such severe aberration relative to an ideal lens, and because the angles are so small, an alternate approach to understanding the optics of gravity is through the theory of light caustics. In my previous blog on the optics of caustics, I described how sets of deflected rays of light become enclosed in envelopes that produce regions of high and low intensity. These envelopes are called caustics. Gravitational light deflection also causes caustics.

In addition to envelopes, it is also possible to trace the time delays caused by gravity on wavefronts. In the regions of the caustic envelopes, these wavefronts can fold back onto themselves so that different parts of the image arrive at different times coming from different directions.

An example of gravitational caustics is shown in Fig. 4. Rays are incident vertically on a gravitational thin lens which deflects the rays so that they overlap in the region below the lens. The red curves are selected wavefronts at three successively later times. The gravitational potential causes a time delay on the propgating front, with greater delays in regions of stronger gravitational potential. The envelope function that is tangent to the rays is called the caustic, here shown as the dense blue mesh. In this case there is a cusp in the caustic near z = -1 below the lens. The wavefronts become multiple-valued past the cusp

Fig. 4 Wavefronts (in red) perpendicular to the rays (in blue) from gravitational deflection of light. A cusp in the wavefront forms at the apex of the caustic ray envelope near z = -1. Farther from the lens the wavefront becomes double-valued, leading to different time delays for the two images if the object is off the optic axis. (All angle are greatly exaggerated.)

The intensity of the distant object past the lens is concentrated near the caustic envelope. The intensity of the caustic at z = -6 is shown in Fig. 5. The ring structure is the cross-sectional spatial intensity at the fixed observation plane, but a transform to the an angular image is one-to-one, so the caustic intensity distribution is also similar to the view of the Einstein ring from a position at z = -6 on the optic axis.

Fig. 5 Simulated caustic of an Einstein arc. This is the cross-sectional intensity at z = -6 from Fig. 4.

The gravitational potential is a function of the mass distribution in the gravitational lens. A different distribution with a flatter distribution of mass near the optic axis is shown in Fig. 6. There are multiple caustics in this case with multi-valued wavefronts. Because caustics are sensitive to mass distribution in the gravitational lens, astronomical observations of gravitational caustics can be used to back out the mass distribution, including dark matter or even distant exoplanets.

Fig. 6 Wavefronts and caustic for a much flatter mass distribution in the galaxy. The wavefront has multiple cusps in this case and the caustic has a double ring. The details of the caustics caused by the gravitational lens can provide insight into the mass distribution of the lensing object.

By David D. Nolte, April 5, 2021

Python Code gravfront.py

(Python code on GitHub.)

#!/usr/bin/env python3
# -*- coding: utf-8 -*-
"""
Created on Tue Mar 30 19:47:31 2021

gravfront.py

@author: David Nolte
Introduction to Modern Dynamics, 2nd edition (Oxford University Press, 2019)

Gravitational Lensing
"""

import numpy as np
from matplotlib import pyplot as plt

plt.close('all')

def refindex(x):
    n = n0/(1 + abs(x)**expon)**(1/expon);
    return n


delt = 0.001
Ly = 10
Lx = 5
n0 = 1
expon = 2   # adjust this from 1 to 10


delx = 0.01
rng = np.int(Lx/delx)
x = delx*np.linspace(-rng,rng)

n = refindex(x)

dndx = np.diff(n)/np.diff(x)

plt.figure(1)
lines = plt.plot(x,n)

plt.figure(2)
lines2 = plt.plot(dndx)

plt.figure(3)
plt.xlim(-Lx, Lx)
plt.ylim(-Ly, 2)
Nloop = 160;
xd = np.zeros((Nloop,3))
yd = np.zeros((Nloop,3))
for loop in range(0,Nloop):
    xp = -Lx + 2*Lx*(loop/Nloop)
    plt.plot([xp, xp],[2, 0],'b',linewidth = 0.25)

    thet = (refindex(xp+delt) - refindex(xp-delt))/(2*delt)
    xb = xp + np.tan(thet)*Ly
    plt.plot([xp, xb],[0, -Ly],'b',linewidth = 0.25)
    
    for sloop in range(0,3):
        delay = n0/(1 + abs(xp)**expon)**(1/expon) - n0
        dis = 0.75*(sloop+1)**2 - delay
        xfront = xp + np.sin(thet)*dis
        yfront = -dis*np.cos(thet)
                
        xd[loop,sloop] = xfront
        yd[loop,sloop] = yfront
        
for sloop in range(0,3):
    plt.plot(xd[:,sloop],yd[:,sloop],'r',linewidth = 0.5)

References

[1] J. Renn, T. Sauer and J. Stachel, “The Origin of Gravitational Lensing: A Postscript to Einstein’s 1936 Science Paper, Science 275. 184 (1997)

[2] A. Einstein, “Lens-Like Action of a Star by the Deviation of Light in the Gravitational Field”, Science 84, 506 (1936)

[3] (Here is an excellent review article on the topic.) J. Wambsganss, “Gravitational lensing as a powerful astrophysical tool: Multiple quasars, giant arcs and extrasolar planets,” Annalen Der Physik, vol. 15, no. 1-2, pp. 43-59, Jan-Feb (2006) SpringerLink

From Oxford Press: Interference (2023)

Read the stories of the scientists and engineers who tamed light and used it to probe the universe.

Order from Amazon.

Order from Oxford U Press

Order from Barnes & Nobles

January 18, 2021November 27, 2023 by David D. Nolte

A Short History of the Photon

The quantum of light—the photon—is a little over 100 years old. It was born in 1905 when Einstein merged Planck’s blackbody quantum hypothesis with statistical mechanics and concluded that light itself must be quantized. No one believed him! Fast forward to today, and the photon is a modern workhorse of modern quantum technology. Quantum encryption and communication are performed almost exclusively with photons, and many prototype quantum computers are optics based. Quantum optics also underpins atomic and molecular optics (AMO), which is one of the hottest and most rapidly advancing frontiers of physics today.

Only after the availability of “quantum” light sources … could photon numbers be manipulated at will, launching the modern era of quantum optics.

This blog tells the story of the early days of the photon and of quantum optics. It begins with Einstein in 1905 and ends with the demonstration of photon anti-bunching that was the first fundamentally quantum optical phenomenon observed seventy years later in 1977. Across that stretch of time, the photon went from a nascent idea in Einstein’s fertile brain to the most thoroughly investigated quantum particle in the realm of physics.

The Photon: Albert Einstein (1905)

When Planck presented his quantum hypothesis in 1900 to the German Physical Society [1], his model of black body radiation retained all its classical properties but one—the quantized interaction of light with matter. He did not think yet in terms of quanta, only in terms of steps in a continuous interaction.

The quantum break came from Einstein when he published his 1905 paper proposing the existence of the photon—an actual quantum of light that carried with it energy and momentum [2]. His reasoning was simple and iron-clad, resting on Planck’s own blackbody relation that Einstein combined with simple reasoning from statistical mechanics. He was led inexorably to the existence of the photon. Unfortunately, almost no one believed him (see my blog on Einstein and Planck).

This was before wave-particle duality in quantum thinking, so the notion that light—so clearly a wave phenomenon—could be a particle was unthinkable. It had taken half of the 19^th century to rid physics of Newton’s corpuscules and emmisionist theories of light, so to bring it back at the beginning of the 20^th century seemed like a great blunder. However, Einstein persisted.

In 1909 he published a paper on the fluctuation properties of light [3] in which he proposed that the fluctuations observed in light intensity had two contributions: one from the discreteness of the photons (what we call “shot noise” today) and one from the fluctuations in the wave properties. Einstein was proposing that both particle and wave properties contributed to intensity fluctuations, exhibiting simultaneous particle-like and wave-like properties. This was one of the first expressions of wave-particle duality in modern physics.

In 1916 and 1917 Einstein took another bold step and proposed the existence of stimulated emission [4]. Once again, his arguments were based on simple physics—this time the principle of detailed balance—and he was led to the audacious conclusion that one photon can stimulated the emission of another. This would become the basis of the laser forty-five years later.

While Einstein was confident in the reality of the photon, others sincerely doubted its existence. Robert Milliken (1868 – 1953) decided to put Einstein’s theory of photoelectron emission to the most stringent test ever performed. In 1915 he painstakingly acquired the definitive dataset with the goal to refute Einstein’s hypothesis, only to confirm it in spectacular fashion [5]. Partly based on Milliken’s confirmation of Einstein’s theory of the photon, Einstein was awarded the Nobel Prize in Physics in 1921.

From that point onward, the physical existence of the photon was accepted and was incorporated routinely into other physical theories. Compton used the energy and the momentum of the photon in 1922 to predict and measure Compton scattering of x-rays off of electrons [6]. The photon was given its modern name by Gilbert Lewis in 1926 [7].

Single-Photon Interference: Geoffry Taylor (1909)

If a light beam is made up of a group of individual light quanta, then in the limit of very dim light, there should just be one photon passing through an optical system at a time. Therefore, to do optical experiments on single photons, one just needs to reach the ultimate dim limit. As simple and clear as this argument sounds, it has problems that only were sorted out after the Hanbury Brown and Twiss experiments in the 1950’s and the controversy they launched (see below). However, in 1909, this thinking seemed like a clear approach for looking for deviations in optical processes in the single-photon limit.

In 1909, Geoffry Ingram Taylor (1886 – 1975) was an undergraduate student at Cambridge University and performed a low-intensity Young’s double-slit experiment (encouraged by J. J. Thomson). At that time the idea of Einstein’s photon was only 4 years old, and Bohr’s theory of the hydrogen atom was still a year away. But Thomson believed that if photons were real, then their existence could possibly show up as deviations in experiments involving single photons. Young’s double-slit experiment is the classic demonstration of the classical wave nature of light, so performing it under conditions when (on average) only a single photon was in transit between a light source and a photographic plate seemed like the best place to look.

The experiment was performed by finding an optimum exposure of photographic plates in a double slit experiment, then reducing the flux while increasing the exposure time, until the single-photon limit was achieved while retaining the same net exposure of the photographic plate. Under the lowest intensity, when only a single photon was in transit at a time (on average), Taylor performed the exposure for three months. To his disappointment, when he developed the film, there was no significant difference between high intensity and low intensity interference fringes [8]. If photons existed, then their quantized nature was not showing up in the low-intensity interference experiment.

The reason that there is no single-photon-limit deviation in the behavior of the Young double-slit experiment is because Young’s experiment only measures first-order coherence properties. The average over many single-photon detection events is described equally well either by classical waves or by quantum mechanics. Quantized effects in the Young experiment could only appear in fluctuations in the arrivals of photons, but in Taylor’s day there was no way to detect the arrival of single photons.

Quantum Theory of Radiation : Paul Dirac (1927)

After Paul Dirac (1902 – 1984) was awarded his doctorate from Cambridge in 1926, he received a stipend that sent him to work with Niels Bohr (1885 – 1962) in Copenhagen. His attention focused on the electromagnetic field and how it interacted with the quantized states of atoms. Although the electromagnetic field was the classical field of light, it was also the quantum field of Einstein’s photon, and he wondered how the quantized harmonic oscillators of the electromagnetic field could be generated by quantum wavefunctions acting as operators. He decided that, to generate a photon, the wavefunction must operate on a state that had no photons—the ground state of the electromagnetic field known as the vacuum state.

Dirac put these thoughts into their appropriate mathematical form and began work on two manuscripts. The first manuscript contained the theoretical details of the non-commuting electromagnetic field operators. He called the process of generating photons out of the vacuum “second quantization”. In second quantization, the classical field of electromagnetism is converted to an operator that generates quanta of the associated quantum field out of the vacuum (and also annihilates photons back into the vacuum). The creation operators can be applied again and again to build up an N-photon state containing N photons that obey Bose-Einstein statistics, as they must, as required by their integer spin, and agreeing with Planck’s blackbody radiation.

Dirac then showed how an interaction of the quantized electromagnetic field with quantized energy levels involved the annihilation and creation of photons as they promoted electrons to higher atomic energy levels, or demoted them through stimulated emission. Very significantly, Dirac’s new theory explained the spontaneous emission of light from an excited electron level as a direct physical process that creates a photon carrying away the energy as the electron falls to a lower energy level. Spontaneous emission had been explained first by Einstein more than ten years earlier when he derived the famous A and B coefficients [4], but the physical mechanism for these processes was inferred rather than derived. Dirac, in late 1926, had produced the first direct theory of photon exchange with matter [9].

Einstein-Podolsky-Rosen (EPR) and Bohr (1935)

The famous dialog between Einstein and Bohr at the Solvay Conferences culminated in the now famous “EPR” paradox of 1935 when Einstein published (together with B. Podolsky and N. Rosen) a paper that contained a particularly simple and cunning thought experiment. In this paper, not only was quantum mechanics under attack, but so was the concept of reality itself, as reflected in the paper’s title “Can Quantum Mechanical Description of Physical Reality Be Considered Complete?” [10].

Bohr and Einstein at Paul Ehrenfest’s house in 1925.

Einstein considered an experiment on two quantum particles that had become “entangled” (meaning they interacted) at some time in the past, and then had flown off in opposite directions. By the time their properties are measured, the two particles are widely separated. Two observers each make measurements of certain properties of the particles. For instance, the first observer could choose to measure either the position or the momentum of one particle. The other observer likewise can choose to make either measurement on the second particle. Each measurement is made with perfect accuracy. The two observers then travel back to meet and compare their measurements. When the two experimentalists compare their data, they find perfect agreement in their values every time that they had chosen (unbeknownst to each other) to make the same measurement. This agreement occurred either when they both chose to measure position or both chose to measure momentum.

It would seem that the state of the particle prior to the second measurement was completely defined by the results of the first measurement. In other words, the state of the second particle is set into a definite state (using quantum-mechanical jargon, the state is said to “collapse”) the instant that the first measurement is made. This implies that there is instantaneous action at a distance −− violating everything that Einstein believed about reality (and violating the law that nothing can travel faster than the speed of light). He therefore had no choice but to consider this conclusion of instantaneous action to be false. Therefore quantum mechanics could not be a complete theory of physical reality −− some deeper theory, yet undiscovered, was needed to resolve the paradox.

Bohr, on the other hand, did not hold “reality” so sacred. In his rebuttal to the EPR paper, which he published six months later under the identical title [11], he rejected Einstein’s criterion for reality. He had no problem with the two observers making the same measurements and finding identical answers. Although one measurement may affect the conditions of the second despite their great distance, no information could be transmitted by this dual measurement process, and hence there was no violation of causality. Bohr’s mind-boggling viewpoint was that reality was nonlocal, meaning that in the quantum world the measurement at one location does influence what is measured somewhere else, even at great distance. Einstein, on the other hand, could not accept a nonlocal reality.

Entangled versus separable states. When the states are separable, no measurement on photon A has any relation to measurements on photon B. However, in the entangled case, all measurements on A are related to measurements on B (and vice versa) regardless of what decision is made to make what measurement on either photon, or whether the photons are separated by great distance. The entangled wave-function is “nonlocal” in the sense that it encompasses both particles at the same time, no matter how far apart they are.

The Intensity Interferometer: Hanbury Brown and Twiss (1956)

Optical physics was surprisingly dormant from the 1930’s through the 1940’s. Most of the research during this time was either on physical optics, like lenses and imaging systems, or on spectroscopy, which was more interested in the physical properties of the materials than in light itself. This hiatus from the photon was about to change dramatically, not driven by physicists, but driven by astronomers.

The development of radar technology during World War II enabled the new field of radio astronomy both with high-tech receivers and with a large cohort of scientists and engineers trained in radio technology. In the late 1940’s and early 1950’s radio astronomy was starting to work with long baselines to better resolve radio sources in the sky using interferometery. The first attempts used coherent references between two separated receivers to provide a common mixing signal to perform field-based detection. However, the stability of the reference was limiting, especially for longer baselines.

In 1950, a doctoral student in the radio astronomy department of the University of Manchester, R. Hanbury Brown, was given the task to design baselines that could work at longer distances to resolve smaller radio sources. After struggling with the technical difficulties of providing a coherent “local” oscillator for distant receivers, Hanbury Brown had a sudden epiphany one evening. Instead of trying to reference the field of one receiver to the field of another, what if, instead, one were to reference the intensity of one receiver to the intensity of the other, specifically correlating the noise on the intensity? To measure intensity requires no local oscillator or reference field. The size of an astronomical source would then show up in how well the intensity fluctuations correlated with each other as the distance between the receivers was changed. He did a back of the envelope calculation that gave him hope that his idea might work, but he needed more rigorous proof if he was to ask for money to try out his idea. He tracked down Richard Twiss at a defense research lab and the two working out the theory of intensity correlations for long-baseline radio interferometry. Using facilities at the famous Jodrell Bank Radio Observatory at Manchester, they demonstrated the principle of their intensity interferometer and measured the angular size of Cygnus A and Cassiopeia A, two of the strongest radio sources in the Northern sky.

One of the surprising side benefits of the intensity interferometer over field-based interferometry was insensitivity to environmental phase fluctuations. For radio astronomy the biggest source of phase fluctuations was the ionosphere, and the new intensity interferometer was immune to its fluctuations. Phase fluctuations had also been the limiting factor for the Michelson stellar interferometer which had limited its use to only about half a dozen stars, so Hanbury Brown and Twiss decided to revisit visible stellar interferometry using their new concept of intensity interferometry.

To illustrate the principle for visible wavelengths, Hanbury Brown and Twiss performed a laboratory experiment to correlate intensity fluctuations in two receivers illuminated by a common source through a beam splitter. The intensity correlations were detected and measured as a function of path length change, illustrating an excess correlation in noise for short path lengths that decayed as the path length increased. They published their results in Nature magazine in 1956 that immediately ignited a firestorm of protest from physicists [12].

In the 1950’s, many physicists had embraced the discrete properties of the photon and had developed a misleading mental picture of photons as individual and indivisible particles that could only go one way or another from a beam splitter, but not both. Therefore, the argument went, if the photon in an attenuated beam was detected in one detector at the output of a beam splitter, then it cannot be detected at the other. This would produce an anticorrelation in coincidence counts at the two detectors. However, the Hanbury Brown Twiss (HBT) data showed a correlation from the two detectors. This launched an intense controversy in which some of those who accepted the results called for a radical new theory of the photon, while most others dismissed the HBT results as due to systematics in the light source. The heart of this controversy was quickly understood by the Nobel laureate E. M Purcell. He correctly pointed out that photons are bosons and are indistinguishable discrete particles and hence are likely to “bunch” together, according to quantum statistics, even under low light conditions [13]. Therefore, attenuated “chaotic” light would indeed show photodetector correlations, even if the average photon number was less than a single photon at a time, the photons would still bunch.

The bunching of photons in light is a second order effect that moves beyond the first-order interference effects of Young’s double slit, but even here the quantum nature of light is not required. A semiclassical theory of light emission from a spectral line with a natural bandwidth also predicts intensity correlations, and the correlations are precisely what would be observed for photon bunching. Therefore, even the second-order HBT results, when performed with natural light sources, do not distinguish between classical and quantum effects in the experimental results. But this reliance on natural light sources was about to change fundmaentally with the invention of the laser.

Invention of the Laser : Ted Maiman (1959)

One of the great scientific breakthroughs of the 20th century was the nearly simultaneous yet independent realization by several researchers around 1951 (by Charles H. Townes of Columbia University, by Joseph Weber of the University of Maryland, and by Alexander M. Prokhorov and Nikolai G. Basov at the Lebedev Institute in Moscow) that clever techniques and novel apparati could be used to produce collections of atoms that had more electrons in excited states than in ground states. Such a situation is called a population inversion. If this situation could be attained, then according to Einstein’s 1917 theory of photon emission, a single photon would stimulate a second photon, which in turn would stimulate two additional electrons to emit two identical photons to give a total of four photons −− and so on. Clearly this process turns a single photon into a host of photons, all with identical energy and phase.

Charles Townes and his research group were the first to succeed in 1953 in producing a device based on ammonia molecules that could work as an intense source of coherent photons. The initial device did not amplify visible light, but amplified microwave photons that had wavelengths of about 3 centimeters. They called the process microwave amplification by stimulated emission of radiation, hence the acronym “MASER”. Despite the significant breakthrough that this invention represented, the devices were very expensive and difficult to operate. The maser did not revolutionize technology, and some even quipped that the acronym stood for “Means of Acquiring Support for Expensive Research”. The maser did, however, launch a new field of study, called quantum electronics, that was the direct descendant of Einstein’s 1917 paper. Most importantly, the existence and development of the maser became the starting point for a device that could do the same thing for light.

The race to develop an optical maser (later to be called laser, for light amplification by stimulated emission of radiation) was intense. Many groups actively pursued this holy grail of quantum electronics. Most believed that it was possible, which made its invention merely a matter of time and effort. This race was won by Theodore H. Maiman at Hughes Research Laboratory in Malibu California in 1960 [14]. He used a ruby crystal that was excited into a population inversion by an intense flash tube (like a flash bulb) that had originally been invented for flash photography. His approach was amazingly simple −− blast the ruby with a high-intensity pulse of light and see what comes out −− which explains why he was the first. Most other groups had been pursuing much more difficult routes because they believed that laser action would be difficult to achieve.

Perhaps the most important aspect of Maiman’s discovery was that it demonstrated that laser action was actually much simpler than people anticipated, and that laser action is a fairly common phenomenon. His discovery was quickly repeated by other groups, and then additional laser media were discovered such as helium-neon gas mixtures, argon gas, carbon dioxide gas, garnet lasers and others. Within several years, over a dozen different material and gas systems were made to lase, opening up wide new areas of research and development that continues unabated to this day. It also called for new theories of optical coherence to explain how coherent laser light interacted with matter.

Coherent States : Glauber (1963)

The HBT experiment had been performed with attenuated chaotic light that had residual coherence caused by the finite linewidth of the filtered light source. The theory of intensity correlations for this type of light was developed in the 1950’s by Emil Wolf and Leonard Mandel using a semiclassical theory in which the statistical properties of the light was based on electromagnetics without a direct need for quantized photons. The HBT results were fully consistent with this semiclassical theory. However, after the invention of the laser, new “coherent” light sources became available that required a fundamentally quantum depiction.

Roy Glauber was a theoretical physicist who received his PhD working with Julian Schwinger at Harvard. He spent several years as a post-doc at Princeton’s Institute for Advanced Study starting in 1949 at the time when quantum field theory was being developed by Schwinger, Feynman and Dyson. While Feynman was off in Brazil for a year learning to play the bongo drums, Glauber filled in for his lectures at Cal Tech. He returned to Harvard in 1952 in the position of an assistant professor. He was already thinking about the quantum aspects of photons in 1956 when news of the photon correlations in the HBT experiment were published, and when the laser was invented three years later, he began developing a theory of photon correlations in laser light that he suspected would be fundamentally different than in natural chaotic light.

Because of his background in quantum field theory, and especially quantum electrodynamics, it was a fairly easy task to couch the quantum optical properties of coherent light in terms of Dirac’s creation and annihilation operators of the electromagnetic field. Related to the minimum-uncertainty wave functions derived initially by Schrödinger in the late 1920’s, Glauber developed a “coherent state” operator that was a minimum uncertainty state of the quantized electromagnetic field [15]. This coherent state represents a laser operating well above the lasing threshold and predicted that the HBT correlations would vanish. Glauber was awarded the Nobel Prize in Physics in 2005 for his work on such “Glauber” states in quantum optics.

Single-Photon Optics: Kimble and Mandel (1977)

Beyond introducing coherent states, Glauber’s new theoretical approach, and parallel work by George Sudarshan around the same time [16], provided a new formalism for exploring quantum optical properties in which fundamentally quantum processes could be explored that could not be predicted using only semiclassical theory. For instance, one could envision producing photon states in which the photon arrivals at a detector could display the kind of anti-bunching that had originally been assumed (in error) by the critics of the HBT experiment. A truly one-photon state, also known as a Fock state or a number state, would be the extreme limit in which the quantum field possessed a single quantum that could be directed at a beam splitter and would emerge either from one side or the other with complete anti-correlation. However, generating such a state in the laboratory remained a challenge.

In 1975 by Carmichel and Walls predicted that resonance fluorescence could produce quantized fields that had lower correlations than coherent states [17]. In 1977 H. J. Kimble, M. Dagenais and L. Mandel demonstrated, for the first time, photon antibunching between two photodetectors at the two ports of a beam splitter [18]. They used a beam of sodium atoms pumped by a dye laser.

This first demonstration of photon antibunching represents a major milestone in the history of quantum optics. Taylor’s first-order experiments in 1909 showed no difference between classical electromagnetic waves and a flux of photons. Similarly the second-order HBT experiment of 1956 using chaotic light could be explained equally well using classical or quantum approaches to explain the observed photon correlations. Even laser light (when the laser is operated far above threshold) produced classic “classical” wave effects with only the shot noise demonstrating the discreteness of photon arrivals. Only after the availability of “quantum” light sources, beginning with the work of Kimble and Mandel, could photon numbers be manipulated at will, launching the modern era of quantum optics. Later experiments by them and others have continually improved the control of photon states.

By David D. Nolte, Jan. 18, 2021

TimeLine:

1900 – Planck (1901). “Law of energy distribution in normal spectra.” Annalen Der Physik 4(3): 553-563.
1905 – A. Einstein (1905). “Generation and conversion of light with regard to a heuristic point of view.” Annalen Der Physik 17(6): 132-148.
1909 – A. Einstein (1909). “On the current state of radiation problems.” Physikalische Zeitschrift 10: 185-193.
1909 – G.I. Taylor: Proc. Cam. Phil. Soc. Math. Phys. Sci. 15 , 114 (1909) Single photon double-slit experiment
1915 – Millikan, R. A. (1916). “A direct photoelectric determination of planck’s “h.”.” Physical Review 7(3): 0355-0388. Photoelectric effect.
1916 – Einstein, A. (1916). “Strahlungs-Emission un -Absorption nach der Quantentheorie.” Verh. Deutsch. Phys. Ges. 18: 318.. Einstein predicts stimulated emission
1923 –Compton, Arthur H. (May 1923). “A Quantum Theory of the Scattering of X-Rays by Light Elements”. Physical Review. 21 (5): 483–502.
1926 – Lewis, G. N. (1926). “The conservation of photons.” Nature 118: 874-875.. Gilbert Lewis named “photon”
1927 – D. Dirac, P. A. M. (1927). “The quantum theory of the emission and absorption of radiation.” Proceedings of the Royal Society of London Series a-Containing Papers of a Mathematical and Physical Character 114(767): 243-265.
1932 – E. P. Wigner: Phys. Rev. 40, 749 (1932)
1935 – A. Einstein, B. Podolsky, N. Rosen: Phys. Rev. 47 , 777 (1935). EPR paradox.
1935 – N. Bohr: Phys. Rev. 48 , 696 (1935). Bohr’s response to the EPR paradox.
1956 – R. Hanbury-Brown, R.W. Twiss: Nature 177 , 27 (1956) Photon bunching
1963 – R. J. Glauber: Phys. Rev. 130 , 2529 (1963) Coherent states
1963 – E. C. G. Sudarshan: Phys. Rev. Lett. 10, 277 (1963) Coherent states
1964 – P. L. Kelley, W.H. Kleiner: Phys. Rev. 136 , 316 (1964)
1966 – F. T. Arecchi, E. Gatti, A. Sona: Phys. Rev. Lett. 20 , 27 (1966); F.T. Arecchi, Phys. Lett. 16 , 32 (1966)
1966 – J. S. Bell: Physics 1 , 105 (1964); Rev. Mod. Phys. 38 , 447 (1966) Bell inequalities
1967 – R. F. Pfleegor, L. Mandel: Phys. Rev. 159 , 1084 (1967) Interference at single photon level
1967 – M. O. Scully, W.E. Lamb: Phys. Rev. 159 , 208 (1967). Quantum theory of laser
1967 – B. R. Mollow, R. J. Glauber: Phys. Rev. 160, 1097 (1967); 162, 1256 (1967) Parametric converter
1969 – M. O. Scully, W.E. Lamb: Phys. Rev. 179 , 368 (1969). Quantum theory of laser
1969 – M. Lax, W.H. Louisell: Phys. Rev. 185 , 568 (1969). Quantum theory of laser
1975 – Carmichael, H. J. and D. F. Walls (1975). Journal of Physics B-Atomic Molecular and Optical Physics 8(6): L77-L81. Photon anti-bunching predicted in resonance fluorescence
1977 – H. J. Kimble, M. Dagenais and L. Mandel (1977) Photon antibunching in resonance fluorescence. Phys. Rev. Lett. 39, 691-5: Kimble, Dagenais and Mandel demonstrate the effect of antibunching

References

• Parts of this blog are excerpted from Mind at Light Speed, D. Nolte (Free Press, 2001) that tells the story of light’s central role in telecommunications and in the future of optical and quantum computers. Further information can be found in Interference: The History of Optical Interferometry and the Scientists who Tamed Light (Oxford, 2023).

[1] Planck (1901). “Law of energy distribution in normal spectra.” Annalen Der Physik 4(3): 553-563.

[2] A. Einstein (1905). “Generation and conversion of light with regard to a heuristic point of view.” Annalen Der Physik 17(6): 132-148

[3] A. Einstein (1909). “On the current state of radiation problems.” Physikalische Zeitschrift 10: 185-193.

[4] Einstein, A. (1916). “Strahlungs-Emission un -Absorption nach der Quantentheorie.” Verh. Deutsch. Phys. Ges. 18: 318; Einstein, A. (1917). “Quantum theory of radiation.” Physikalische Zeitschrift 18: 121-128.

[5] Millikan, R. A. (1916). “A direct photoelectric determination of planck‘s “h.”.” Physical Review 7(3): 0355-0388.

[6] Compton, A. H. (1923). “A quantum theory of the scattering of x-rays by light elements.” Physical Review 21(5): 0483-0502.

[7] Lewis, G. N. (1926). “The conservation of photons.” Nature 118: 874-875.

[8] Taylor, G. I. (1910). “Interference fringes with feeble light.” Proceedings of the Cambridge Philosophical Society 15: 114-115.

[9] Dirac, P. A. M. (1927). “The quantum theory of the emission and absorption of radiation.” Proceedings of the Royal Society of London Series a-Containing Papers of a Mathematical and Physical Character 114(767): 243-265.

EinsteinPR35 Download

[10] Einstein, A., B. Podolsky and N. Rosen (1935). “Can quantum-mechanical description of physical reality be considered complete?” Physical Review 47(10): 0777-0780.

BohrPR35 Download

[11] Bohr, N. (1935). “Can quantum-mechanical description of physical reality be considered complete?” Physical Review 48(8): 696-702.

• Hanbury Brown 1956 Download

[12] Brown, R. H. and R. Q. Twiss (1956). “Correlation Between Photons in 2 Coherent Beams of Light.” Nature 177(4497): 27-29; [1] R. H. Brown and R. Q. Twiss, “Test of a new type of stellar interferometer on Sirius,” Nature, vol. 178, no. 4541, pp. 1046-1048, (1956).

• Purcell 1956 Download

[13] Purcell, E. M. (1956). “Question of Correlation Between Photons in Coherent Light Rays.” Nature 178(4548): 1448-1450.

[14] Maimen, T. H. (1960). “Stimulated optical radiation in ruby.” Nature 187: 493.

• Glauber 1963 Download

[15] Glauber, R. J. (1963). “Photon Correlations.” Physical Review Letters 10(3): 84.

[16] Sudarshan, E. C. G. (1963). “Equivalence of semiclassical and quantum mechanical descriptions of statistical light beams.” Physical Review Letters 10(7): 277-&.; Mehta, C. L. and E. C. Sudarshan (1965). “Relation between quantum and semiclassical description of optical coherence.” Physical Review 138(1B): B274.

• Carmichel 1975 Download

[17] Carmichael, H. J. and D. F. Walls (1975). “Quantum treatment of spontaneous emission from a strongly driven 2-level atom.” Journal of Physics B-Atomic Molecular and Optical Physics 8(6): L77-L81.

[18] Kimble, H. J., M. Dagenais and L. Mandel (1977). “Photon anti bunching in resonance fluorescence.” Physical Review Letters 39(11): 691-695.

Interference (New from Oxford University Press, 2023)

A popular account of the trials and toils of the scientists and engineers who tamed light and used it to probe the universe.

Available at Amazon

and at Oxford University Press

and at Barnes & Noble

March 2, 2020October 24, 2023 by David D. Nolte

A Commotion in the Stars: The History of the Doppler Effect

Christian Andreas Doppler (1803 – 1853) was born in Salzburg, Austria, to a longstanding family of stonemasons. As a second son, he was expected to help his older brother run the business, so his Father had him tested in his 18^th year for his suitability for a career in business. The examiner Simon Stampfer (1790 – 1864), an Austrian mathematician and inventor teaching at the Lyceum in Salzburg, discovered that Doppler had a gift for mathematics and was better suited for a scientific career. Stampfer’s enthusiasm convinced Doppler’s father to enroll him in the Polytechnik Institute in Vienna (founded only a few years earlier in 1815) where he took classes in mathematics, mechanics and physics [1] from 1822 to 1825. Doppler excelled in his courses, but was dissatisfied with the narrowness of the education, yearning for more breadth and depth in his studies and for more significance in his positions, feelings he would struggle with for his entire short life. He left Vienna, returning to the Lyceum in Salzburg to round out his education with philosophy, languages and poetry. Unfortunately, this four-year detour away from technical studies impeded his ability to gain a permanent technical position, so he began a temporary assistantship with a mathematics professor at Vienna. As he approached his 30^th birthday this term expired without prospects. He was about to emigrate to America when he finally received an offer to teach at a secondary school in Prague.

To read about the attack by Joseph Petzval on Doppler’s effect and the effect it had on Doppler, see my feature article “The Fall and Rise of the Doppler Effect“ in Physics Today, 73(3) 30, March (2020).

Salzburg Austria

Doppler in Prague

Prague gave Doppler new life. He was a professor with a position that allowed him to marry the daughter of a sliver and goldsmith from Salzburg. He began to publish scholarly papers, and in 1837 was appointed supplementary professor of Higher Mathematics and Geometry at the Prague Technical Institute, promoted to full professor in 1841. It was here that he met the unusual genius Bernard Bolzano (1781 – 1848), recently returned from political exile in the countryside. Bolzano was a philosopher and mathematician who developed rigorous concepts of mathematical limits and is famous today for his part in the Bolzano-Weierstrass theorem in functional analysis, but he had been too liberal and too outspoken for the conservative Austrian regime and had been dismissed from the University in Prague in 1819. He was forbidden to publish his work in Austrian journals, which is one reason why much of Bolzano’s groundbreaking work in functional analysis remained unknown during his lifetime. However, he participated in the Bohemian Society for Science from a distance, recognizing the inventive tendencies in the newcomer Doppler and supporting him for membership in the Bohemian Society. When Bolzano was allowed to return in 1842 to the Polytechnic Institute in Prague, he and Doppler became close friends as kindred spirits.

Prague, Czech Republic

On May 25, 1842, Bolzano presided as chairman over a meeting of the Bohemian Society for Science on the day that Doppler read a landmark paper on the color of stars to a meagre assembly of only five regular members of the Society [2]. The turn-out was so small that the meeting may have been held in the robing room of the Society rather than in the meeting hall itself. Leading up to this famous moment, Doppler’s interests were peripatetic, ranging widely over mathematical and physical topics, but he had lately become fascinated by astronomy and by the phenomenon of stellar aberration. Stellar aberration was discovered by James Bradley in 1729 and explained as the result of the Earth’s yearly motion around the Sun, causing the apparent location of a distant star to change slightly depending on the direction of the Earth’s motion. Bradley explained this in terms of the finite speed of light and was able to estimate it to within several percent [3]. As Doppler studied Bradley aberration, he wondered how the relative motion of the Earth would affect the color of the star. By making a simple analogy of a ship traveling with, or against, a series of ocean waves, he concluded that the frequency of impact of the peaks and troughs of waves on the ship was no different than the arrival of peaks and troughs of the light waves impinging on the eye. Because perceived color was related to the frequency of excitation in the eye, he concluded that the color of light would be slightly shifted to the blue if approaching, and to the red if receding from, the light source.

Doppler wave fronts from a source emitting spherical waves moving with speeds β relative to the speed of the wave in the medium.

Doppler calculated the magnitude of the effect by taking a simple ratio of the speed of the observer relative to the speed of light. What he found was that the speed of the Earth, though sufficient to cause the detectable aberration in the position of stars, was insufficient to produce a noticeable change in color. However, his interest in astronomy had made him familiar with binary stars where the relative motion of the light source might be high enough to cause color shifts. In fact, in the star catalogs there were examples of binary stars that had complementary red and blue colors. Therefore, the title of his paper, published in the Proceedings of the Royal Bohemian Society of Sciences a few months after he read it to the society, was “On the Coloured Light of the Double Stars and Certain Other Stars of the Heavens: Attempt at a General Theory which Incorporates Bradley’s Theorem of Aberration as an Integral Part” [4].

Title page of Doppler’s 1842 paper introducing the Doppler Effect.

Doppler’s analogy was correct, but like all analogies not founded on physical law, it differed in detail from the true nature of the phenomenon. By 1842 the transverse character of light waves had been thoroughly proven through the work of Fresnel and Arago several decades earlier, yet Doppler held onto the old-fashioned notion that light was composed of longitudinal waves. Bolzano, fully versed in the transverse nature of light, kindly published a commentary shortly afterwards [5] showing how the transverse effect for light, and a longitudinal effect for sound, were both supported by Doppler’s idea. Yet Doppler also did not know that speeds in visual binaries were too small to produce noticeable color effects to the unaided eye. Finally, (and perhaps the greatest flaw in his argument on the color of stars) a continuous spectrum that extends from the visible into the infrared and ultraviolet would not change color because all the frequencies would shift together preserving the flat (white) spectrum.

The simple algebraic derivation of the Doppler Effect in the 1842 publication..

Doppler’s twelve years in Prague were intense. He was consumed by his Society responsibilities and by an extremely heavy teaching load that included personal exams of hundreds of students. The only time he could be creative was during the night while his wife and children slept. Overworked and running on too little rest, his health already frail with the onset of tuberculosis, Doppler collapsed, and he was unable to continue at the Polytechnic. In 1847 he transferred to the School of Mines and Forrestry in Schemnitz (modern Banská Štiavnica in Slovakia) with more pay and less work. Yet the revolutions of 1848 swept across Europe, with student uprisings, barricades in the streets, and Hungarian liberation armies occupying the cities and universities, giving him no peace. Providentially, his former mentor Stampfer retired from the Polytechnic in Vienna, and Doppler was called to fill the vacancy.

Although Doppler was named the Director of Austria’s first Institute of Physics and was elected to the National Academy, he ran afoul of one of the other Academy members, Joseph Petzval (1807 – 1891), who persecuted Doppler and his effect. To read a detailed description of the attack by Petzval on Doppler’s effect and the effect it had on Doppler, see my feature article “The Fall and Rise of the Doppler Effect” in Physics Today, March issue (2020).

Christian Doppler

Voigt’s Transformation

It is difficult today to appreciate just how deeply engrained the reality of the luminiferous ether was in the psyche of the 19^th century physicist. The last of the classical physicists were reluctant even to adopt Maxwell’s electromagnetic theory for the explanation of optical phenomena, and as physicists inevitably were compelled to do so, some of their colleagues looked on with dismay and disappointment. This was the situation for Woldemar Voigt (1850 – 1919) at the University of Göttingen, who was appointed as one of the first professors of physics there in 1883, to be succeeded in later years by Peter Debye and Max Born. Voigt received his doctorate at the University of Königsberg under Franz Neumann, exploring the elastic properties of rock salt, and at Göttingen he spent a quarter century pursuing experimental and theoretical research into crystalline properties. Voigt’s research, with students like Paul Drude, laid the foundation for the modern field of solid state physics. His textbook Lehrbuch der Kristallphysik published in 1910 remained influential well into the 20^th century because it adopted mathematical symmetry as a guiding principle of physics. It was in the context of his studies of crystal elasticity that he introduced the word “tensor” into the language of physics.

At the January 1887 meeting of the Royal Society of Science at Göttingen, three months before Michelson and Morely began their reality-altering experiments at the Case Western Reserve University in Cleveland Ohio, Voit submitted a paper deriving the longitudinal optical Doppler effect in an incompressible medium. He was responding to results published in 1886 by Michelson and Morely on their measurements of the Fresnel drag coefficient, which was the precursor to their later results on the absolute motion of the Earth through the ether.

Fresnel drag is the effect of light propagating through a medium that is in motion. The French physicist Francois Arago (1786 – 1853) in 1810 had attempted to observe the effects of corpuscles of light emitted from stars propagating with different speeds through the ether as the Earth spun on its axis and traveled around the sun. He succeeded only in observing ordinary stellar aberration. The absence of the effects of motion through the ether motivated Augustin-Jean Fresnel (1788 – 1827) to apply his newly-developed wave theory of light to explain the null results. In 1818 Fresnel derived an expression for the dragging of light by a moving medium that explained the absence of effects in Arago’s observations. For light propagating through a medium of refractive index n that is moving at a speed v, the resultant velocity of light is

where the last term in parenthesis is the Fresnel drag coefficient. The Fresnel drag effect supported the idea of the ether by explaining why its effects could not be observed—a kind of Catch-22—but it also applied to light moving through a moving dielectric medium. In 1851, Fizeau used an interferometer to measure the Fresnel drag coefficient for light moving through moving water, arriving at conclusions that directly confirmed the Fresnel drag effect. The positive experiments of Fizeau, as well as the phenomenon of stellar aberration, would be extremely influential on the thoughts of Einstein as he developed his approach to special relativity in 1905. They were also extremely influential to Michelson, Morley and Voigt.

In his paper on the absence of the Fresnel drag effect in the first Michelson-Morley experiment, Voigt pointed out that an equation of the form

is invariant under the transformation

From our modern vantage point, we immediately recognize (to within a scale factor) the Lorentz transformation of relativity theory. The first equation is common Galilean relativity, but the last equation was something new, introducing a position-dependent time as an observer moved with speed relative to the speed of light [6]. Using these equations, Voigt was the first to derive the longitudinal (conventional) Doppler effect from relativistic effects.

Voigt’s derivation of the longitudinal Doppler effect used a classical approach that is still used today in Modern Physics textbooks to derive the Doppler effect. The argument proceeds by considering a moving source that emits a continuous wave in the direction of motion. Because the wave propagates at a finite speed, the moving source chases the leading edge of the wave front, catching up by a small amount by the time a single cycle of the wave has been emitted. The resulting compressed oscillation represents a blue shift of the emitted light. By using his transformations, Voigt arrived at the first relativistic expression for the shift in light frequency. At low speeds, Voigt’s derivation reverted to Doppler’s original expression.

A few months after Voigt delivered his paper, Michelson and Morley announced the results of their interferometric measurements of the motion of the Earth through the ether—with their null results. In retrospect, the Michelson-Morley experiment is viewed as one of the monumental assaults on the old classical physics, helping to launch the relativity revolution. However, in its own day, it was little more than just another null result on the ether. It did incite Fitzgerald and Lorentz to suggest that length of the arms of the interferometer contracted in the direction of motion, with the eventual emergence of the full Lorentz transformations by 1904—seventeen years after the Michelson results.

In 1904 Einstein, working in relative isolation at the Swiss patent office, was surprisingly unaware of the latest advances in the physics of the ether. He did not know about Voigt’s derivation of the relativistic Doppler effect (1887) as he had not heard of Lorentz’s final version of relativistic coordinate transformations (1904). His thinking about relativistic effects focused much farther into the past, to Bradley’s stellar aberration (1725) and Fizeau’s experiment of light propagating through moving water (1851). Einstein proceeded on simple principles, unencumbered by the mental baggage of the day, and delivered his beautifully minimalist theory of special relativity in his famous paper of 1905 “On the Electrodynamics of Moving Bodies”, independently deriving the Lorentz coordinate transformations [7].

One of Einstein’s talents in theoretical physics was to predict new phenomena as a way to provide direct confirmation of a new theory. This was how he later famously predicted the deflection of light by the Sun and the gravitational frequency shift of light. In 1905 he used his new theory of special relativity to predict observable consequences that included a general treatment of the relativistic Doppler effect. This included the effects of time dilation in addition to the longitudinal effect of the source chasing the wave. Time dilation produced a correction to Doppler’s original expression for the longitudinal effect that became significant at speeds approaching the speed of light. More significantly, it predicted a transverse Doppler effect for a source moving along a line perpendicular to the line of sight to an observer. This effect had not been predicted either by Doppler or by Voigt. The equation for the general Doppler effect for any observation angle is

Just as Doppler had been motivated by Bradley’s aberration of starlight when he conceived of his original principle for the longitudinal Doppler effect, Einstein combined the general Doppler effect with his results for the relativistic addition of velocities (also in his 1905 Annalen paper) as the conclusive treatment of stellar aberration nearly 200 years after Bradley first observed the effect.

Despite the generally positive reception of Einstein’s theory of special relativity, some of its consequences were anathema to many physicists at the time. A key stumbling block was the question whether relativistic effects, like moving clocks running slowly, were only apparent, or were actually real, and Einstein had to fight to convince others of its reality. When Johannes Stark (1874 – 1957) observed Doppler line shifts in ion beams called “canal rays” in 1906 (Stark received the 1919 Nobel prize in part for this discovery) [8], Einstein promptly published a paper suggesting how the canal rays could be used in a transverse geometry to directly detect time dilation through the transverse Doppler effect [9]. Thirty years passed before the experiment was performed with sufficient accuracy by Herbert Ives and G. R. Stilwell in 1938 to measure the transverse Doppler effect [10]. Ironically, even at this late date, Ives and Stilwell were convinced that their experiment had disproved Einstein’s time dilation by supporting Lorentz’ contraction theory of the electron. The Ives-Stilwell experiment was the first direct test of time dilation, followed in 1940 by muon lifetime measurements [11].

Notes

[1] pg. 15, Eden, A. (1992). The search for Christian Doppler. Wien, Springer-Verlag.

[2] pg. 30, Eden

[3] Bradley, J (1729). “Account of a new discoved Motion of the Fix’d Stars”. Phil Trans. 35: 637–660.

[4] C. A. DOPPLER, “Über das farbige Licht der Doppelsterne und einiger anderer Gestirne des Himmels (About the coloured light of the binary stars and some other stars of the heavens),” Proceedings of the Royal Bohemian Society of Sciences, vol. V, no. 2, pp. 465–482, (Reissued 1903) (1842).

[5] B. Bolzano, “Ein Paar Bemerkunen über die Neu Theorie in Herrn Professor Ch. Doppler’s Schrift “Über das farbige Licht der Doppersterne und eineger anderer Gestirnedes Himmels”,” Pogg. Anal. der Physik und Chemie, vol. 60, p. 83, 1843; B. Bolzano, “Christian Doppler’s neuste Leistunen af dem Gebiet der physikalischen Apparatenlehre, Akoustik, Optik and optische Astronomie,” Pogg. Anal. der Physik und Chemie, vol. 72, pp. 530-555, 1847.

[6] W. Voigt, “Uber das Doppler’sche Princip,” Göttinger Nachrichten, vol. 7, pp. 41–51, (1887). The common use of c to express the speed of light came later from Voigt’s student Paul Drude.

[7] A. Einstein, “On the electrodynamics of moving bodies,” Annalen Der Physik, vol. 17, pp. 891-921, 1905.

[8] J. Stark, W. Hermann, and S. Kinoshita, “The Doppler effect in the spectrum of mercury,” Annalen Der Physik, vol. 21, pp. 462-469, Nov 1906.

[9] A. Einstein, “”Über die Möglichkeit einer neuen Prüfung des Relativitätsprinzips”,” vol. 328, pp. 197–198, 1907.

[10] H. E. Ives and G. R. Stilwell, “An experimental study of the rate of a moving atomic clock,” Journal of the Optical Society of America, vol. 28, p. 215, 1938.

[11] B. Rossi and D. B. Hall, “Variation of the Rate of Decay of Mesotrons with Momentum,” Physical Review, vol. 59, pp. 223–228, 1941.

May 30, 2019November 14, 2023 by David D. Nolte

The Iconic Eikonal and the Optical Path

Nature loves the path of steepest descent. Place a ball on a smooth curved surface and release it, and it will instantansouly accelerate in the direction of steepest descent. Shoot a laser beam from an oblique angle onto a piece of glass to hit a target inside, and the path taken by the beam is the only path that decreases the distance to the target in the shortest time. Diffract a stream of electrons from the surface of a crystal, and quantum detection events are greatest at the positions where the troughs and peaks of the deBroglie waves converge the most. The first example is Newton’s second law. The second example is Fermat’s principle and Snell’s Law. The third example is Feynman’s path-integral formulation of quantum mechanics. They all share in common a minimization principle—the principle of least action—that the path of a dynamical system is the one that minimizes a property known as “action”.

The Eikonal Equation is the “F = ma” of ray optics. It’s solutions describe the paths of light rays through complicated media.

The principle of least action, first proposed by the French physicist Maupertuis through mechanical analogy, became a principle of Lagrangian mechanics in the hands of Lagrange, but was still restricted to mechanical systems of particles. The principle was generalized forty years later by Hamilton, who began by considering the propagation of light waves, and ended by transforming mechanics into a study of pure geometry divorced from forces and inertia. Optics played a key role in the development of mechanics, and mechanics returned the favor by giving optics the Eikonal Equation. The Eikonal Equation is the “F = ma” of ray optics. It’s solutions describe the paths of light rays through complicated media.

Malus’ Theorem

Anyone who has taken a course in optics knows that Étienne-Louis Malus (1775-1812) discovered the polarization of light, but little else is taught about this French mathematician who was one of the savants Napoleon had taken along with himself when he invaded Egypt in 1798. After experiencing numerous horrors of war and plague, Malus returned to France damaged but wiser. He discovered the polarization of light in the Fall of 1808 as he was playing with crystals of icelandic spar at sunset and happened to view last rays of the sun reflected from the windows of the Luxumbourg palace. Icelandic spar produces double images in natural light because it is birefringent. Malus discovered that he could extinguish one of the double images of the Luxumbourg windows by rotating the crystal a certain way, demonstrating that light is polarized by reflection. The degree to which light is extinguished as a function of the angle of the polarizing crystal is known as Malus’ Law.

Fronts-piece to the *Description de l’Égypte* , the first volume published by Joseph Fourier in 1808 based on the report of the savants of *L’Institute de l’Égypte* that included Monge, Fourier and Malus, among many other French scientists and engineers.

Malus had picked up an interest in the general properties of light and imaging during lulls in his ordeal in Egypt. (To read about Malus’ misadventures during Napoleon’s campaign in Egypt, see Chapter 1 of Interference.) He was an emissionist following his compatriot Laplace, rather than an undulationist following Thomas Young. It is ironic that the French scientists were staunchly supporting Newton on the nature of light, while the British scientist Thomas Young was trying to upend Netwonian optics. Almost all physicists at that time were emissionists, only a few years after Young’s double-slit experiment of 1804, and few serious scientists accepted Young’s theory of the wave nature of light until Fresnel and Arago supplied the rigorous theory and experimental proofs much later in 1819.

Malus’ Theorem states that rays perpendicular to an initial surface are perpendicular to a later surface after reflection in an optical system. This theorem is the starting point for the Eikonal ray equation, as well as for modern applications in adaptive optics. This figure shows a propagating aberrated wavefront that is “compensated” by a deformable mirror to produce a tight focus.

As a prelude to his later discovery of polarization, Malus had earlier proven a theorem about trajectories that particles of light take through an optical system. One of the key questions about the particles of light in an optical system was how they formed images. The physics of light particles moving through lenses was too complex to treat at that time, but reflection was relatively easy based on the simple reflection law. Malus proved a theorem mathematically that after a reflection from a curved mirror, a set of rays perpendicular to an initial nonplanar surface would remain perpendicular at a later surface after reflection (this property is closely related to the conservation of optical etendue). This is known as Malus’ Theorem, and he thought it only held true after a single reflection, but later mathematicians proved that it remains true even after an arbitrary number of reflections, even in cases when the rays intersect to form an optical effect known as a caustic. The mathematics of caustics would catch the interest of an Irish mathematician and physicist who helped launch a new field of mathematical physics.

Hamilton’s Characteristic Function

William Rowan Hamilton (1805 – 1865) was a child prodigy who taught himself thirteen languages by the time he was thirteen years old (with the help of his linguist uncle), but mathematics became his primary focus at Trinity College at the University in Dublin. His mathematical prowess was so great that he was made the Astronomer Royal of Ireland while still an undergraduate student. He also became fascinated in the theory of envelopes of curves and in particular to the mathematics of caustic curves in optics.

In 1823 at the age of 18, he wrote a paper titled Caustics that was read to the Royal Irish Academy. In this paper, Hamilton gave an exceedingly simple proof of Malus’ Law, but that was perhaps the simplest part of the paper. Other aspects were mathematically obscure and reviewers requested further additions and refinements before publication. Over the next four years, as Hamilton expanded this work on optics, he developed a new theory of optics, the first part of which was published as Theory of Systems of Rays in 1827 with two following supplements completed by 1833 but never published.

Hamilton’s most important contribution to optical theory (and eventually to mechanics) he called his characteristic function. By applying the principle of Fermat’s least time, which he called his principle of stationary action, he sought to find a single unique function that characterized every path through an optical system. By first proving Malus’ Theorem and then applying the theorem to any system of rays using the principle of stationary action, he was able to construct two partial differential equations whose solution, if it could be found, defined every ray through the optical system. This result was completely general and could be extended to include curved rays passing through inhomogeneous media. Because it mapped input rays to output rays, it was the most general characterization of any defined optical system. The characteristic function defined surfaces of constant action whose normal vectors were the rays of the optical system. Today these surfaces of constant action are called the Eikonal function (but how it got its name is the next chapter of this story). Using his characteristic function, Hamilton predicted a phenomenon known as conical refraction in 1832, which was subsequently observed, launching him to a level of fame unusual for an academic.

Once Hamilton had established his principle of stationary action of curved light rays, it was an easy step to extend it to apply to mechanical systems of particles with curved trajectories. This step produced his most famous work On a General Method in Dynamics published in two parts in 1834 and 1835 [1] in which he developed what became known as Hamiltonian dynamics. As his mechanical work was extended by others including Jacobi, Darboux and Poincaré, Hamilton’s work on optics was overshadowed, overlooked and eventually lost. It was rediscovered when Schrödinger, in his famous paper of 1926, invoked Hamilton’s optical work as a direct example of the wave-particle duality of quantum mechanics [2]. Yet in the interim, a German mathematician tackled the same optical problems that Hamilton had seventy years earlier, and gave the Eikonal Equation its name.

Bruns’ Eikonal

The German mathematician Heinrich Bruns (1848-1919) was engaged chiefly with the measurement of the Earth, or geodesy. He was a professor of mathematics in Berlin and later Leipzig. One claim fame was that one of his graduate students was Felix Hausdorff [3] who would go on to much greater fame in the field of set theory and measure theory (the Hausdorff dimension was a precursor to the fractal dimension). Possibly motivated by his studies done with Hausdorff on refraction of light by the atmosphere, Bruns became interested in Malus’ Theorem for the same reasons and with the same goals as Hamilton, yet was unaware of Hamilton’s work in optics.

The mathematical process of creating “images”, in the sense of a mathematical mapping, made Bruns think of the Greek word εικων which literally means “icon” or “image”, and he published a small book in 1895 with the title Das Eikonal in which he derived a general equation for the path of rays through an optical system. His approach was heavily geometrical and is not easily recognized as an equation arising from variational principals. It rediscovered most of the results of Hamilton’s paper on the Theory of Systems of Rays and was thus not groundbreaking in the sense of new discovery. But it did reintroduce the world to the problem of systems of rays, and his name of Eikonal for the equations of the ray paths stuck, and was used with increasing frequency in subsequent years. Arnold Sommerfeld (1868 – 1951) was one of the early proponents of the Eikonal equation and recognized its connection with action principles in mechanics. He discussed the Eikonal equation in a 1911 optics paper with Runge [4] and in 1916 used action principles to extend Bohr’s model of the hydrogen atom [5]. While the Eikonal approach was not used often, it became popular in the 1960’s when computational optics made numerical solutions possible.

Lagrangian Dynamics of Light Rays

In physical optics, one of the most important properties of a ray passing through an optical system is known as the optical path length (OPL). The OPL is the central quantity that is used in problems of interferometry, and it is the central property that appears in Fermat’s principle that leads to Snell’s Law. The OPL played an important role in the history of the calculus when Johann Bernoulli in 1697 used it to derive the path taken by a light ray as an analogy of a brachistochrone curve – the curve of least time taken by a particle between two points.

The OPL between two points in a refractive medium is the sum of the piecewise product of the refractive index n with infinitesimal elements of the path length ds. In integral form, this is expressed as

where the “dot” is a derivative with respedt to s. The optical Lagrangian is recognized as

The Lagrangian is inserted into the Euler equations to yield (after some algebra, see Introduction to Modern Dynamics pg. 336)

This is a second-order ordinary differential equation in the variables x^a that define the ray path through the system. It is literally a “trajectory” of the ray, and the Eikonal equation becomes the F = ma of ray optics.

Hamiltonian Optics

In a paraxial system (in which the rays never make large angles relative to the optic axis) it is common to select the position z as a single parameter to define the curve of the ray path so that the trajectory is parameterized as

where the derivatives are with respect to z, and the effective Lagrangian is recognized as

The Hamiltonian formulation is derived from the Lagrangian by defining an optical Hamiltonian as the Legendre transform of the Lagrangian. To start, the Lagrangian is expressed in terms of the generalized coordinates and momenta. The generalized optical momenta are defined as

This relationship leads to an alternative expression for the Eikonal equation (also known as the scalar Eikonal equation) expressed as

where S(x,y,z) = const. is the eikonal function. The momentum vectors are perpendicular to the surfaces of constant S, which are recognized as the wavefronts of a propagating wave.

The Lagrangian can be restated as a function of the generalized momenta as

and the Legendre transform that takes the Lagrangian into the Hamiltonian is

The trajectory of the rays is the solution to Hamilton’s equations of motion applied to this Hamiltonian

Light Orbits

If the optical rays are restricted to the x-y plane, then Hamilton’s equations of motion can be expressed relative to the path length ds, and the momenta are p_a = ndx^a/ds. The ray equations are (simply expressing the 2 second-order Eikonal equation as 4 first-order equations)

where the dot is a derivative with respect to the element ds.

As an example, consider a radial refractive index profile in the x-y plane

where r is the radius on the x-y plane. Putting this refractive index profile into the Eikonal equations creates a two-dimensional orbit in the x-y plane. The Eikonal Equation is the “F = ma” of ray optics. It’s solutions describe the paths of light rays through complicated media, including the phenomenon of gravitational lensing (see my blog post) and the orbits of photons around black holes (see my other blog post).

By David D. Nolte, May 30, 2019

Gaussian refractive index profile in the x-y plane. From raysimple.py.

Ray orbits around the center of the Gaussian refractive index profile. From raysimple.py

Python Code: raysimple.py

The following Python code solves for individual trajectories. (Python code on GitHub.)

#!/usr/bin/env python3
# -*- coding: utf-8 -*-
"""
raysimple.py
Created on Tue May 28 11:50:24 2019
@author: nolte
D. D. Nolte, Introduction to Modern Dynamics: Chaos, Networks, Space and Time, 2nd ed. (Oxford,2019)
"""

import numpy as np
import matplotlib as mpl
from mpl_toolkits.mplot3d import Axes3D
from scipy import integrate
from matplotlib import pyplot as plt
from matplotlib import cm
import time
import os

plt.close('all')

# selection 1 = Gaussian
# selection 2 = Donut
selection = 1

print(' ')
print('raysimple.py')

def refindex(x,y):
    
    if selection == 1:
        
        sig = 10
        
        n = 1 + np.exp(-(x**2 + y**2)/2/sig**2)
        nx = (-2*x/2/sig**2)*np.exp(-(x**2 + y**2)/2/sig**2)
        ny = (-2*y/2/sig**2)*np.exp(-(x**2 + y**2)/2/sig**2)
        
    elif selection == 2:
        
        sig = 10;
        r2 = (x**2 + y**2)
        r1 = np.sqrt(r2)
        np.expon = np.exp(-r2/2/sig**2)
        
        n = 1+0.3*r1*np.expon;
        nx = 0.3*r1*(-2*x/2/sig**2)*np.expon + 0.3*np.expon*2*x/r1
        ny = 0.3*r1*(-2*y/2/sig**2)*np.expon + 0.3*np.expon*2*y/r1
    
        
    return [n,nx,ny]


def flow_deriv(x_y_z,tspan):
    x, y, z, w = x_y_z
    
    n, nx, ny = refindex(x,y)
    
    yp = np.zeros(shape=(4,))
    yp[0] = z/n
    yp[1] = w/n
    yp[2] = nx
    yp[3] = ny
    
    return yp
                
V = np.zeros(shape=(100,100))
for xloop in range(100):
    xx = -20 + 40*xloop/100
    for yloop in range(100):
        yy = -20 + 40*yloop/100
        n,nx,ny = refindex(xx,yy) 
        V[yloop,xloop] = n

fig = plt.figure(1)
contr = plt.contourf(V,100, cmap=cm.coolwarm, vmin = 1, vmax = 3)
fig.colorbar(contr, shrink=0.5, aspect=5)    
fig = plt.show()


v1 = 0.707      # Change this initial condition
v2 = np.sqrt(1-v1**2)
y0 = [12, 0, v1, v2]     # Change these initial conditions

tspan = np.linspace(1,1700,1700)

y = integrate.odeint(flow_deriv, y0, tspan)

plt.figure(2)
lines = plt.plot(y[1:1550,0],y[1:1550,1])
plt.setp(lines, linewidth=0.5)
plt.show()

New from Oxford University Press: Interference and the History of Light and Optics (2023)

Read the stories of the scientists and engineers who tamed light and used it to probe the universe.

Order Today from Amazon.

Order Today from Oxford U Press

Order Today from Barnes & Nobles

Bibliography

An excellent textbook on geometric optics from Hamilton’s point of view is K. B. Wolf, Geometric Optics in Phase Space (Springer, 2004). Another is H. A. Buchdahl, An Introduction to Hamiltonian Optics (Dover, 1992).

A rather older textbook on geometrical optics is by J. L. Synge, Geometrical Optics: An Introduction to Hamilton’s Method (Cambridge University Press, 1962) showing the derivation of the ray equations in the final chapter using variational methods. Synge takes a dim view of Bruns’ term “Eikonal” since Hamilton got there first and Bruns was unaware of it.

A book that makes an especially strong case for the Optical-Mechanical analogy of Fermat’s principle, connecting the trajectories of mechanics to the paths of optical rays is Daryl Holm, Geometric Mechanics: Part I Dynamics and Symmetry (Imperial College Press 2008).

The Eikonal ray equation is derived from the geodesic equation (or rather as a geodesic equation) in D. D. Nolte, Introduction to Modern Dynamics, 2nd-edition (Oxford, 2019).

References

[1] Hamilton, W. R. “On a general method in dynamics I.” Mathematical Papers, I ,103-161: 247-308. (1834); Hamilton, W. R. “On a general method in dynamics II.” Mathematical Papers, I ,103-161: 95-144. (1835)

[2] Schrodinger, E. “Quantification of the eigen-value problem.” Annalen Der Physik 79(6): 489-527. (1926)

[3] For the fateful story of Felix Hausdorff (aka Paul Mongré) see Chapter 9 of Galileo Unbound (Oxford, 2018).

[4] Sommerfeld, A. and J. Runge. “The application of vector calculations on the basis of geometric optics.” Annalen Der Physik 35(7): 277-298. (1911)

[5] Sommerfeld, A. “The quantum theory of spectral lines.” Annalen Der Physik 51(17): 1-94. (1916)

The “What” and “Why” of All-Optical Processing

Nonlinear Optics

All-Optical Regeneration

Photonic Neural Networks

Further Reading

The Wabash Yacht Club

The Telecom Bubble and Bust

Fiber to the Home

Trunk-Line Fiber Optics

Bibliography

Einstein and the Transverse Doppler Effect

A) Transverse Doppler Shift Relative to Emission Angle

B) Transverse Doppler Shift Relative to Angle at Reception

C) Compromise: The Null Transverse Doppler Shift

D) Source in Circular Motion Around Receiver

E) Receiver in Circular Motion Around Source

New from Oxford Press: The History of Light and Interference (2023)

References

The History of Gravitational Lensing

The Optics of Gravity and Light

The Caustic Curves of Einstein Rings

Python Code gravfront.py

References

From Oxford Press: Interference (2023)

The Photon: Albert Einstein (1905)

Single-Photon Interference: Geoffry Taylor (1909)

Quantum Theory of Radiation : Paul Dirac (1927)

Einstein-Podolsky-Rosen (EPR) and Bohr (1935)

The Intensity Interferometer: Hanbury Brown and Twiss (1956)

Invention of the Laser : Ted Maiman (1959)

Coherent States : Glauber (1963)

Single-Photon Optics: Kimble and Mandel (1977)

TimeLine:

References

Interference (New from Oxford University Press, 2023)

Doppler in Prague

Voigt’s Transformation

Further Reading

Notes

Malus’ Theorem

Hamilton’s Characteristic Function

Bruns’ Eikonal

Lagrangian Dynamics of Light Rays

Hamiltonian Optics

Light Orbits

Python Code: raysimple.py

New from Oxford University Press: Interference and the History of Light and Optics (2023)

Bibliography

References